智能电网中的零售商不同时段实时定价策略

张　辰，　党亚峥

(上海理工大学 管理学院, 上海 200093)



指导教师： 党亚峥(1973 -)，女，讲师，博士，主要研究方向为系统优化，E-mail： jgdyz@163.com

智能电网中的零售商不同时段实时定价策略

张辰，党亚峥

(上海理工大学 管理学院, 上海 200093)

摘要：实时定价是智能电网需求侧管理(DSM)的主要手段之一，电力零售商不同时段的供电价格，会影响用户对电力资源的消费。对电力零售商在供电高峰时段定价、低峰时段定价建立Stackelberg博弈模型，分析二者在智能电网实时定价中的策略互动，求出均衡解，使得电力零售商在高峰时段和低峰时段定价，两个时段都获得最大收益。仿真模拟结果验证了此动态实时定价结果的有效性，表明在不同时段进行实时定价的机制下，智能电网中的零售商收益最佳，并且能够可持续经营。

关键词：智能电网; 需求侧管理; 实时定价; Stackelberg模型

智能电网是近年来各个国家研究的一个热门课题，智能电网所具有的特点如下： 减少温室气体排放，有效促进清洁能源的开发与利用，保证能源供应的安全稳定、使能源输送和使用效率大大提高，增强了电网运行中的安全性、可靠性、灵活性，达到电网与用户互动的目的[1]，给用户提供优质便捷的服务，最终促进经济的可持续发展。电价的制定更是一个关乎国家民生的问题，通过实时电价[2]这种计算电价的方式，可以及时将电价告知用电一方，根据自己实际用电需求来更加合理的选择何种用电方式，让电力用户自主调节用电方面的负荷，使电力资源达到最佳能耗[3]。

文献[4]中以电力消费者购买电量最大效用为研究对象，在智能电网中实时定价的机制下，构建消耗不同电量的电力消费者采购电量决策模型；文献[5]中研究在电力市场中使用实时定价的电力消费者数量增加对电力市场经济效益的作用，创建了趸售市场与零售市场竞争的数学模型；文献[6-7]中根据求解出的用户总利润和电力供应商成本之差最大化提出多种电价计算方法，使模型中的用户收益最大以及供应商所花成本最小，文献[8]中指出电力消费者通过获取实时更新的电价消息来合理调整自己的实时电量消费，建立以电力消费者福利最大化为目标的经济数学模型；文献[9-11]中利用博弈知识针对在电力市场中存在的竞价进行分析探讨。本文基于文献[12]探讨了智能电网中的电力零售商不同时段实时定价博弈策略。

1智能电网中的实时定价需求模型

在智能电网中，用户可以从电力零售商在不同供电时段中购电，电力市场是自由化的。我们主要的目标是用户支付最少的电价，而让电力零售商获取更大的收益。考虑到实时变化的电价，能够真正起到削峰填谷的作用。

1.1　电力需求模型

在我们的电力需求模型中，每个用户安装了智能电表。零售商制定实时电力零售价格和信息通过局域网传输给用户。对用户而言，在智能电表中的用电量能够被计算，根据不同用电时间段分配最优的电量能耗。为了使决策执行起来更加高效，每个电力消费者需要了解自身的偏好和电力消费模式。

在电力市场中，本文只探讨研究家庭用户，家庭用户喜欢用最低的电价来消耗更多的电量，家庭用户消耗电能的行为能够用效用函数[13]来描述。文献[14]中规定的用户效用函数改变如下：

U(p,d)=Kd-λd2/2-φpd

(1)

式中，K是一个参数，随家庭用户用电时段不同而变化；d为家庭用户电量消耗需求；φ为电量需求价格弹性；λ为固定不变的参数；p为使用电力零售商的电价。

电力零售商利用实时定价需求侧管理手段来促使家庭用户把自身的电力耗能调整到最大效用，每个家庭用户的电力耗能在用户效用函数中被计算出来，每个以家庭为单位用户的电力需求函数D(p)可以通过最大化其效用函数而得到。即

D(p)=(K-φp)/λ

(2)

1.2　零售商电力需求函数

在提出的方案中，电力零售商有N个不同的供电时段，电力零售商对不同时段使用电力资源的家庭用户所提供的价格是不同的，家庭用户可以避开使用高峰时段的电力价格，而转向电力零售商提供较低电力时段价格，进行合理能耗。电力零售商根据用电时段不同的家庭用户能耗总需求表述如下：

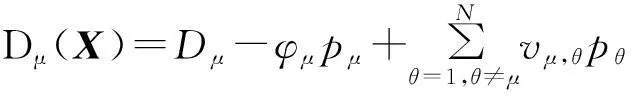
(3)

式中，X是电力零售商不同时段电价向量；Dμ是一个参数，随电力零售商供电时段不同而变化，在Dμ中μ∈(1,2,…,N)；φ(0<φ<1)为电力零售商μ时段采购电量需求价格弹性；pμ为电力零售商在μ时段的电价；pθ为零售商θ时段提供的电价；vμ,θ(0≤vμ,θ≤1)为电力零售商将θ时段的电价信息传送给家庭用户，家庭用户用电量θ时段电价转向使用另一μ时段电价的家庭用户用电量耗电比例，当vμ,θ=0时，家庭用户不能调整自己的用电时段，而当vμ,θ=1时，家庭用户可以根据自身实际用电需要任意调整用电时间段。

1.3　电力零售商收益

电力零售商根据家庭用户消耗的电量需求和零售商所制定的不同时间段的电价，计算自己的获利情况，当零售商向家庭用户供应的电量不能满足家庭用户耗电需求时，零售商会给家庭用户在价格上给予一定比例的优惠，所以电力零售商μ时段的利润可以由以下数学公式来表达：

Rμ(X)=Dμ(X)pμ+MμY-

式中，Mμ为零售商在μ时段提供服务的家庭用户数量，μ∈(1,2,…,N)；Y为电力零售商对家庭用户提供的固定电价；Zμ为折扣比例系数；Dreq为每个家庭用户相同的电力需求；ημ(0≤ημ≤1)为电力零售商购买电量实现因子；Qμ为电力零售商在μ时段购电总量；Cμ为电力零售商在μ时购买电量的成本。

2动态实时定价Stackelberg博弈决策模型

在建立的模型中，电力零售商不同时段、不同电价会影响电力消费者的消费电能决策。因此，博弈论可以用来分析动态实时定价的问题，使得电力零售商在不同时段定价都能获得最大利润。将零售商供电时间段抽象为两类： 一类为高峰时段H，定价为p1；另外一类为低峰时段L，定价设为p2。则电力零售商在高峰时段的利润函数为

RH(p1,p2)=DH(p1,p2)p1+MHY-

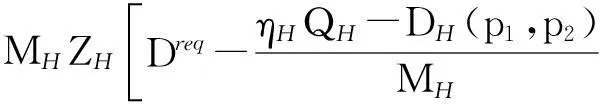
(5)

电力零售商在低峰时段的利润函数为

RL(p1,p2)=DL(p1,p2)p2+MLY-

(6)

式中，DH是一个参数，随电力零售商供电时段H不同而变化；MH为零售商在H时段提供服务的家庭用户人数；ZH为电力零售商H时段提供的折扣系数；ηH(0≤ηH≤1)为电力零售商在H时段购买电量实现因子；QH为电力零售商在H时段购买电总量；CH为电力零售商在H时购电成本；DL是一个参数，随电力零售商供电时段L不同而变化；ML为零售商在L时段提供服务的家庭用户人数；ZL为电力零售商在L时段提供的折扣系数；ηL(0≤ηL≤1)为电力零售商在L时段购买电量实现因子；QL为电力零售商在L时段购买电总量；CL为电力零售商在L时购电成本。

在电力零售商高峰时段定价和低峰时段定价，构造Stackelberg实时定价博弈策略模型。电力零售商先到电力批发商处购买电量，在用电高峰时间段向家庭用户宣布自己的电价p1≥0，电力零售商在已知p1后决定低峰时段的电价p2≥0，这里的p2是p1的一个反应函数，p2=Q2(p1)。电力零售商在高峰时段、低峰时段的利润函数分别如下：

RH(p1,p2)=DH(p1,p2)p1+MHY-

(7)

RL(p1,p2)=DL(p1,p2)p2+MLY-

(8)

计算一个多阶段的数学模型Stackelberg策略博弈得到的是一个子博弈精炼纳什均衡价格[15]，采用逆推归纳法来演算。

在当前时段，电力零售商观察到家庭用户使用其在高峰时段提供的电价p1，由于家庭用户根据自己的实际用电需求，避免高峰时段用电，转向低峰时段用电，电力零售商对低峰时段的电价p2做出反应，最优收益，通过式(8)一阶求导

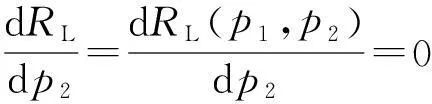
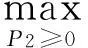
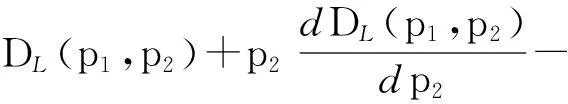
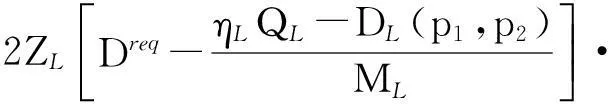
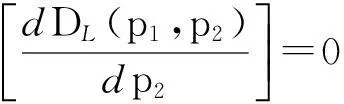
(9)

根据式(3)将

DL(p1,p2)=DL-φLp2+NHvL,Hp1

代入式(9)可得

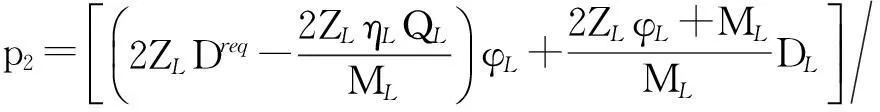
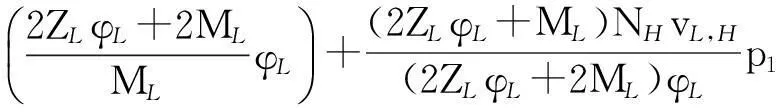
(10)

根据式(10)，设

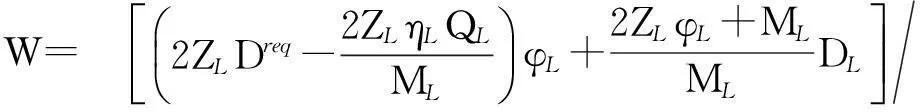
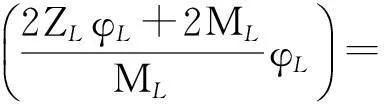
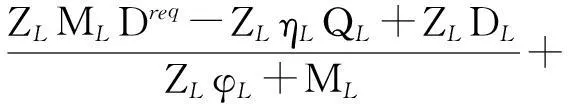
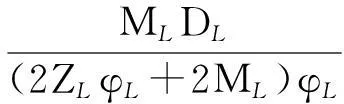
(11)

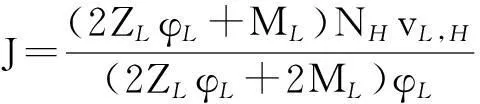
(12)

同时，因为p2是p1的一个反应函数，故有

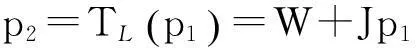
(13)

而电力零售商预知低峰时段电价p2将根据TL(p1) 进行调整价格，所以电力零售商在高峰时段要最大化RH，即

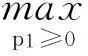
对式(7)最优化一阶条件为

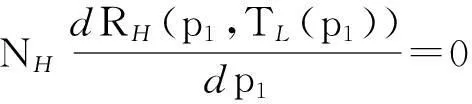
根据式(3)，DH(p1,p2)=DH(p1,TL(p1))与p2=TL(p1)，代入式(7)，可得

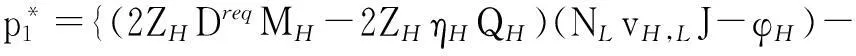
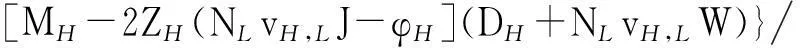
{[2MH-2ZH(NLvH,LJ-φH)](NLvH,LJ-φH)}

(14)

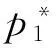
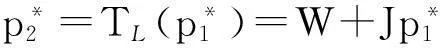
(15)

3仿真实验

为了验证实时定价动态博弈模型的有效性，把电力零售商具体化成两个不同供电时段，高峰时段供电电价为p1，低峰时段供电电价为p2，据式(15)，有

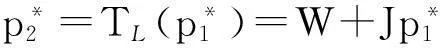
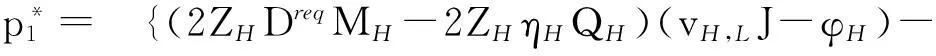
[MH-2ZH(vH,LJ-φH)](DH+vH,LW)}/

{[2MH-2ZH(vH,LJ-φH)](vH,LJ-φH)}

p2=TL(p1)=W+Jp1

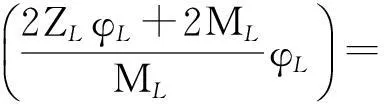
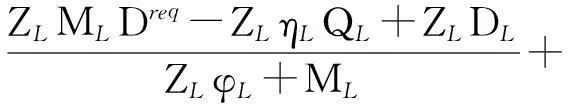
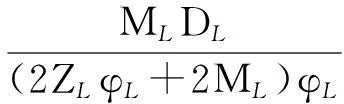
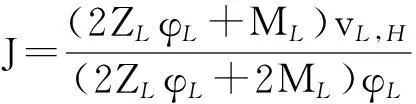
令：φL=φH=0.8，ηH=ηL=0.9，ZH=ZL=0.85，QH=50，QL=10，D=0.5，vH,L=vL,H=v。则有：

(1)DH=20，DL=4，MH=40，ML=8。显然电力零售商对于高峰、低峰时段最理想的实时定价反应式均受到v作用，最优实时电价变动趋向如图1所示，当流动数量比例v变大，均衡价格会变高。

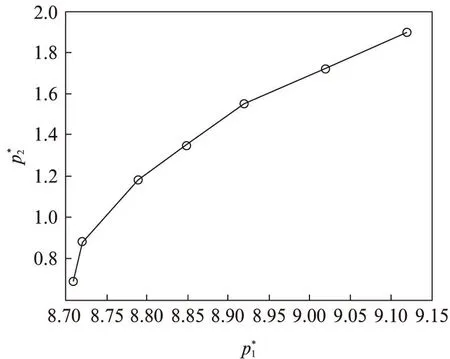
图1　受v影响均衡价格变化趋势图Fig.1　Trend of equilibrium price change affected by v

(2)DH=20，DL=4，vH,L=vL,H=v=0.5，MH=40，ML=8,13,16。在这3种情况下，均衡解的变化趋势如图2。在高峰时段，使用高峰时段用电量一定，而转向低峰时段的用电量在增加时，均衡价格也随之升高。

(3)MH=40，ML=8，vH,L=vL,H=v=0.5，DH=20，DL=4,5,6。这3种情形下均衡解的变化趋势如图3显示在高峰时段，使用电力资源的的家庭用户数量一定，而转向低峰时段的使用电力资源的家庭用户数量在增加时，均衡价格也随之升高。

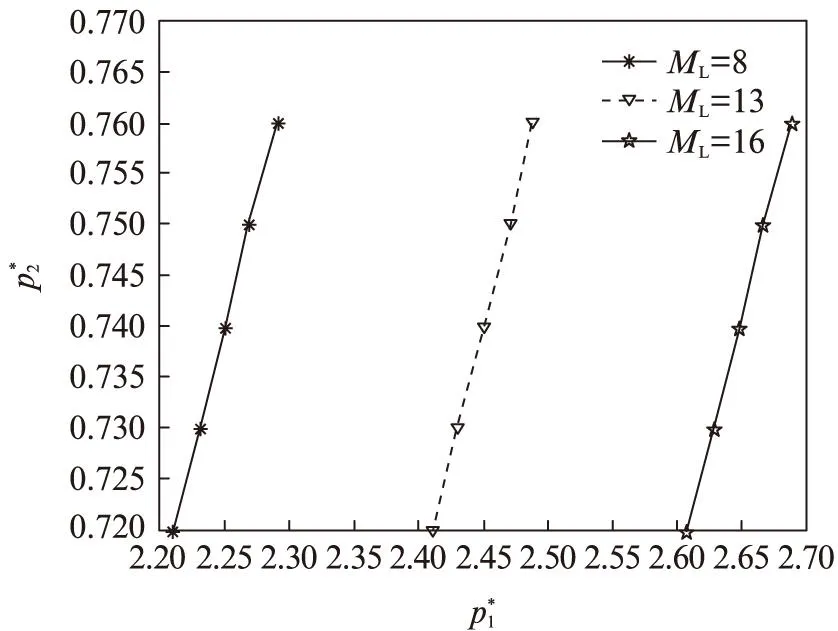
图2　受ML影响均衡价格变化趋势图Fig.2　2 Trend of equilibrium price change affected by ML

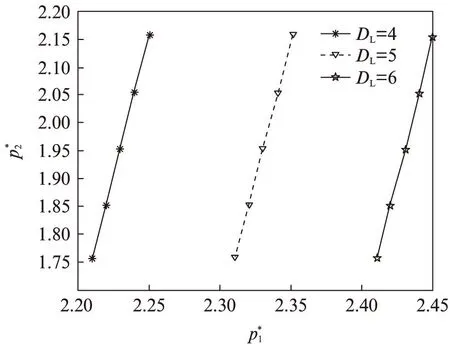
图3　受DL影响均衡价格变化趋势图Fig.3　Trend of equilibrium price change affected by DL

4结语

本文从一种基于电力零售商在不同供电时段向电力消费者提供电量服务着手，利用零售商高峰时段实时定价和低峰时段实时定价，建立实时定价博弈决策方案。为现有的电力市场提供了良好的智能电网实时定价建模手段，根据仿真模拟实验结果，验证了对所提出博弈决策方案的有效性以及相关参数对电力资源采购及价格决策的影响，更好地诠释了智能电网实时定价的动态过程。

参考文献：

[1]梅生伟，朱建全.智能电网中的若干数学问题与控制科学问题及其展望[J].自动化学报，2013，39(2)： 119-131.

[2]周明华,徐敏.基于最优潮流的实时电价及其算法的研究[J].继电器,2006,34(21)： 63-67.

[3]Conejo A J，Morales J M，Baringo L.Real-time demand response model[J].IEEE Transactions on Smart Grid，2010，1(3)： 236-242.

[4]张钦，王锡凡，王秀丽，等.需求侧实时电价下用户购电风险决策[J].电力系统自动化，2008，32(13)： 16-20.

[5]曾鸣，许子智，王江波，等.实时电价用户比例增加对电力市场经济效率的影响[J].电网技术，2010，34(6)： 82-86.

[6]徐伟强，冯兆丽，黄炯，等.基于改进对偶分解的智能电网快速实时定价方法[J].电力系统保护与控制，2012，40(21)： 42-47.

[7]宋文宇，袁光辉，蒋艳.基于混合智能算法的电力系统经济调度优化模型研究[J].上海理工大学学报，2013，35(5)： 469-474.

[8]Asadi G，Gitizadeh M，Roosta A.Welfare maximization under real-time pricing in smart grid using PSO algorithm[C]∥2013 21st Iranian Conference on Electrical Engineering(ICEE).Mashhad: IEEE，2013： 1-7.

[9]梅生伟，龚媛，刘锋.三代电网演化模型及特性分析[J].中国电机工程学报，2014，34(7)： 1003-1012.

[10]谢青洋，应黎明，祝勇刚.基于经济机制设计理论的电力市场竞争机制设计[J].中国电机工程学报，2014，34(10)： 1709-1716.

[11]伍亮，杨金明.基于微分博弈理论的含多电源区域电力系统负荷频率控制[J].中国电机工程学报，2014，34(16)： 2676-2683.

[12]Bu S，Yu F R，Liu P X.Dynamic pricing for demand-side management in the smart grid[C]∥2011 IEEE Online Conference on Green Communications(GreenCom).New York： IEEE，2011： 47-51.

[13]侯芳，吴政球，王良缘.快速实时电价算法[J].电力系统及其自动化学报，2002，14(4)： 32-35.

[14]Bu S R,Yu F R,Liu P X.A game-theoretical decision making scheme for electricity retailers in the smart grid with demand-side management/[C]∥2011 IEEE International Conference on Smart Grid Communications.Brussels： IEEE，2011： 387-391.

[15]张维迎.博弈论与信息经济学[M].上海： 上海人民出版社，2004： 100-109.

Real-time Pricing Strategy for Retailers inDifferent Periods of Smart Grid

ZHANGChen，DANGYazheng

(Business School, University of Shanghai for Scienceand Technology, Shanghai 200093, China)

Abstract：Real-time pricing is a major means of demand-side management (DSM). For electricity retailers supplying electricity in different period, real-time dynamic pricing provides a new real-time pricing game decision-making solution. Electricity supplying price of retailers during different periods will affect the users’electricity consumption. A Stackelberg game model is established for process during peak periods and low peak periods. By analyzing the strategy interaction of both to achieve getting equilibrium, retailers can get maximum profit during high peaks and the low peaks. Simulation results show validity of the real-time dynamic pricing. With the mechanism of real-time pricing in different periods, retailers can gain the optimal revenue and sustainable management of smart grids.

Key words：smart grid; demand-side management (DSM); real-time pricing; Stackelberg model

文献标志码：A

中图分类号：F 407.61

文章编号2095 - 0020(2015)06 -0368 - 05

作者简介：张辰(1988 -)，男，硕士生，主要研究方向为智能电网实时定价，E-mail： zhangc0715@163.com

基金项目：国家自然科学基金项目资助(11171221)；上海市自然科学基金项目资助(0014ZR14282)；上海市科技创新项目资助(15ZZ073)

收稿日期：2015 - 06 - 19