基于倾斜相位的CPM信号调制解调设计*
2015-02-24窦高奇万志毅
陈 飞,窦高奇,高 俊,万志毅
(1. 海军工程大学电子工程学院,武汉 430033;2. 73698部队,南京 210000)
基于倾斜相位的CPM信号调制解调设计*
陈 飞1,窦高奇1,高 俊1,万志毅2
(1. 海军工程大学电子工程学院,武汉 430033;2. 73698部队,南京 210000)
连续相位调制(CPM)信号是一种具有高频谱效率和功率效率的恒包络调制技术,但基于传统相位网格的CPM信号调制解调算法复杂度高、计算量大。提出了一种基于倾斜相位网格的CPM调制解调算法,通过分析CPM相位网络图和分解模型,给出了CPM信号倾斜相位网格设计、状态存储、初始化及译码的实现方法,相比传统相位,该算法更加简洁、计算量更小,并通过仿真验证了设计方案的正确性。
CPM;倾斜相位;调制解调;Vterbi译码
0 引 言
CPM信号具有包络恒定、功率利用率高、频率利用率高等优点,近几年来,随着硬件技术的发展,在移动通信等领域受到了广泛研究与应用[1]。传统相位网格可以完整地描述CPM信号,但其算法较复杂,且状态网格图是时变的[2],即不满足每个符号周期的相位轨迹都是同一个符号周期内可能的相位轨迹集合的时间迁移,但其相隔一个符号周期的相位轨迹是一样的。为了满足时不变,就只能将相邻两个周期的网格图合并,使得m为奇数时相位状态为2P个(调制指数h=m/P)。而在倾斜相位中,相位状态始终是P个,且状态网格图是时不变的,相位状态减少意味着计算量成指数减少[3]。本文在介绍CPM信号倾斜相位分解模型的基本原理的基础上,给出了一种基于倾斜相位网格的CPM调制解调算法,分析了CPM信号倾斜相位网格设计、状态存储、初始化及译码的实现方法,相比传统相位,算法更加简洁、计算量也更小,最后通过仿真验证了设计方案的正确性。
1 CPM的基本原理
1.1 CPM信号定义
一个连续相位调制(CPM)信号的表达式一般可以表示为[4]:
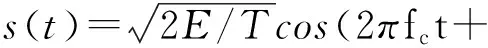
(1)
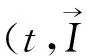

(2)
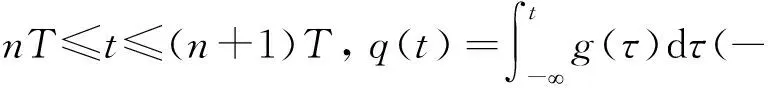
1.2 倾斜相位
一般定义倾斜相位为[2]:
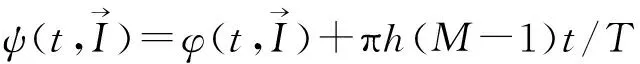
(3)
将式(2)代入式(3),用Ii=2Ui-(M-1)代替式(2)中的符号电平Ii,同时设t=τ+nT,得物理相位[2]:
(4)
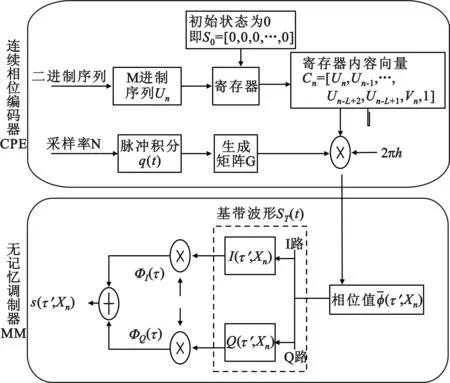
其中,R2π[·]表示模2π运算,0≤τ (5) 1.3 CPM信号分解模型 通过公式4可以发现,CPM信号具备类似于卷积码的记忆特性,因此CPM调制可以分解为一个有限状态的连续相位编码器(CPE),以及一个无记忆调制器(MM)[2,6]。 1.3.1 CPE编码器 根据定义[2]: (6) Vn取值范围为0、1、2、…、(P-1)。由此得:CPE编码器结构框图如图1[2],CPE 的输入为Un,输出为向量Xn: Xn=[Un,Un-1,…,Un-L+2,Un-L+1,Vn] (7) 当输入为更新Un+1时,输出为向量更新Xn+1=[Un+1,Un,…,Un-L+2,Un-L+2,Vn+1],其中 (8) 图1 CPE编码器结构 1.3.2 无记忆调制器MM 将公式(4)代入公式(1)得: (9) 其中,0≤τ≤T,把式(9)分解成为同相分量和正交分量的形式: (10) 2.1 CPE算法设计 将公式(6)代入公式(4),得: (11) 根据公式(5)可以得出: (12) 定义列向量G和行向量Cn如下: G=[q(τ),q((τ+T),…,q(τ+(L-2)T) q(τ+(L-1)T),1,W′(τ)]′ (13) Cn=[Un,Un-1,…,Un-L+2,Un-L+1,Vn,1]=[Xn,1] (14) 对一个符号周期进行N倍过采样,可得到N倍采样时生成矩阵G,代入公式(11)得: (15) 由Cn很容易得出倾斜相位Sn的定义,即: Sn=[Un-1,…,Un-L+2,Un-L+1,Vn] (16) 2.2 状态存储 相位状态Sn有P·ML-1个状态,向量Xn和Cn有P·ML个状态,为了方便计算机处理这些向量,需要建立Sn、Xn和Cn到十进制j的一一映射。 2.2.1L>1时Sn、Xn和Cn到十进制j的映射 为方便描述,下面举例说明如何将Sj映射到十进制j,如M=2,L=3,h=1/2=m/p,Sj=[Un-1,Un-2,Vn]=[1,1,1] 时,首先将[Un-1,Un-2]由M进制转换成十进制:[Un-1,Un-2]=Un-1×M1+Un-1×M0=1×21+1×20=3,再加上VnML-1=1×23-1=4,得j=3+4=7,因此S7=[Un-1,Un-2,Vn]=[1,1,1]。 类似地也可以建立Xn到十进制j的一一映射。X15=[Un,Un-1,Un-2,Vn]=[1,1,1,2]。显然,由公式(14)可知Xn和Cn是一一映射的,所以它们的十进制映射是完全一样的。同时不难发现,Xn和Cn到十进制的映射过程同关联长度L增加1时Sn到十进制的映射过程在数学上是等效的,因此一个映射函数就可以表示所有映射。 2.2.2L>1时Sn、Xn和Cn到十进制j的映射 当L=1、M=4、h=1/2时,Un∈{0,1,2,3},Sn∈{0,1},初始相位为S0,当输入符号为2和0时,状态转移的终止相位都是S0,出现了相位转移的初始和终止状态与输入符号之间非一一映射。为了避免这种情况发生,L= 1时,定义Sn=[Un-1,Vn],即和L=2时的状态定义一样。根据2.2.1节所述,Sn、Xn和Cn到十进制的映射过程都与L=2时的Sn的映射过程等效。但公式(8)还按照L=1时进行转移,即Vn+1=Rp[Vn+Un]。 2.2.3 状态初始化 为了简单统一,初始化时,令网格图始终从初始状态S0=[0,0,…,0,0]开始,那么式(4)中累积相位就不再从U0开始,而是从U-(L-1)开始,更新为: 相应地公式(5)更新为: 公式(12)更新为: 结合前面的论述,CPM倾斜相位调制相关的算法都已清楚明了,调制框图如图2所示。 图2 网格调制框图 2.3 Vterbi译码算法设计 CPM信号解调,最常用的方法就是Vterbi算法[7],Vterbi最大似然序列检测步骤包括基带波形匹配, 分支度量计算、路径度量更新、确定幸存路径和译码[7-9]。 2.3.1 基带波形匹配 2.3.2 分支度量Meitric的计算 2.3.3 路径度量更新、确定幸存路径和译码 计算出倾斜相位状态网格中每一条边e的Meitric值后,再将每条路径所有边e的Meitric值累加,最后在到达每一个节点的所有路径中选择累加值最小的路径作为幸存路径,循环往复直到网格图最后一级,得出整个网格图的幸存路径,再根据幸存路径中每条边e与输入符号Un的一一映射关系,得到译码序列[8]。结合前面的推导,CPM倾斜相位解调相关的算法都已清楚明了,解调框图如图3所示。 3.1 调制波形 取符号率10 KHz,每符号周期采样次数128次,载波频率10 KHz,h=0.5,M=4,L=1,载波幅度A=1,初始状态S0。输入序列为320 231,仿真结果如图4所示。图中,输入符号分别为3、2、1、0时调制信号输出频率分别为17.5 k、12.5 k、7.5 k、2.5 k,与理论结果相符。说明L=1时状态转移过程中已不存在非一一映射的问题。 图4 L=1时非一一映射问题的验证波形 3.2 误码率 3.2.1 不同符号数目的误误比特率 图5为GMSK时,符号数目M分别为2、4、8时的误比特率,由图可知在非强噪声情况下,随着符号数目(进制数)M的增加,可以得到较大的性能增益。 图5 GMSK时不同符号数目的误比特率 3.2.2 不同关联长度和调制指数的误误比特率 图6中h=0.75,M=2时L分别为1、3、5时的REC的误比特率,从图中可以看出,误比特性能按照L=3、L=1、L=5的顺序逐渐变差。将图6 中的调制指数变大为h=1.5,其它参数不变,仿真结果如图7所示,误比特性能随着L的增大越来越好。综合图6和图7可以得出:当(记忆)关联长度L增加时,h也必须增加,才能获得较大的性能增益。 图6 h=0.75,M=2,REC时不同L的误比特率 图7 h=1.5,M=2,REC时不同L的误比特率 本文研究了基于倾斜相位的CPM信号调制解调算法的设计与实现,并利用MATLAB进行了仿真。结果表明,相比传统相位网格算法,利用倾斜相位进行CPM信号网格调制解调算法更加简洁,更利于过程分析,计算量也更小。计算量和误码性能是一对矛盾体,本文中维特比解调算法的计算量较大,误码性能较好,可以根据需要采用其它解调算法。如:低复杂度的次优检测器算法可以降低计算量,但误码性能也会变差;通用BCJR算法会使计算量进一步变大,但误码性能也会变好,可以根据现实需要,实现计算量和误码性能的有效折衷。 [1] 李燕斌,骆小谚,李寅博.部分响应CPM信号解调器的FPGA设计[J].通信技术,2011,44(02)13. LI Yan-bin, LUO Xiao-yan, LI Yin-bo. FPGA Design of Partial Response CPM Signal Demodulator [J]. Communications Technology, 2011, 44(02)13. [2] Rimoldi B.A Deeomposition Approaeh to CPM[J] . IEEE Trans.Inf.Theory.1988,34:260-270. [3] Massey J L. “The How and Why of Channel Coding,” [J]. in Proc. 1984 Int. Zurich Seminar on Digital Communication, Mar. 1984, pp. El.1-E1.7. [4] John G Proakis.Ditital Communications(Fourth Edition)[M]. Publishing House of Electronics Industry, 2001: 205-215. [5] Benedetto S, Dicsalar D, Montorsi G. Soft-Output Decoding Algorithms in Iterative Decoding of Turbo Codes[Z]. TDA Progress Report, Feb 1998. pp. 42-124. [6] Tor aulin. Continuous Phase Modulation[J]. IEEETransactions on Communications, 1981, 29(3):196-225. [7] Forney G D. “The Viterbi Algorithm,” [J]. Proc. IEEE, vol. 61, pp. 268-278, Mar. 1973. [8] Anderson, Aulin J, Sundberg B T. Digital Phase Modulation[M]. New York: Plenum, 1986:271-353. [9] 彭伟智,李小文.TD-SCDMA系统中Viterbi算法研究与改进[J].通信技术,2007,40(11):105-106. PENG Wei -zhi,LI Xiao-wen. Research and Improvement of Viterbi Algorithm in TD-SCDMA System [J]. Communications Technology, 2007, 40(11):105-106. CPM Signals Modulation and Demodulation based on Tilted Phase CHEN Fei1,DOU Gao-qi1,GAO Jun1,WAN Zhi-yi2 (1.College of Electronic Engineering, Naval University of Engineering,Wuhan Hubei 430033,China;2.Unit 73698 of PLA,Nanjing Jiangsu 210000,China) CPM (Continuous Phase Modulation) signal is a kind of constant-envelope digital modulation with both high spectral and power efficiency,and however,for the high algorithm complexity and large calculation of traditional CPM modulation and demodulation based on phase trellis, a CPM modulation and demodulation algorithm based on tilted-phase trellis is proposed. Based on analysis of CPM phase network plannning and decomposition model, the implementation methods of tilted-phase gridding design, state storage, initialzation and decoding of CPM signals are also given. Compared with traditional phase, the tilted-phase algorithm enjoys less complexity and calculation, and finally the simulation indicates the correctness of this design scheme. CPM;tilted-phase;modulation and demodulation; Viterbi coding 10.3969/j.issn.1002-0802.2015.05.007 2015-01-14; 2015-04-14 Received date:2015-01-14;Revised date:2015-04-14 文献标志码:A 文章编号:1002-0802(2015)05-0541-05 陈 飞(1987—),男,硕士研究生,工程师,主要研究方向为信号调制与编码技术; 窦高奇(1981—),男,博士,讲师,主要研究方向为迭代检测和估计; 高 俊(1957—),男,博士生导师,教授,主要研究方向为通信理论与技术; 万志毅(1989—),男,助理工程师,主要研究方向为光纤通信与信息处理。


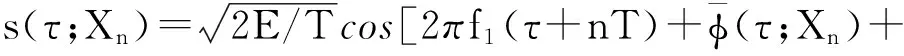
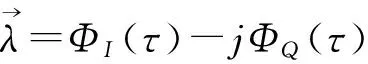
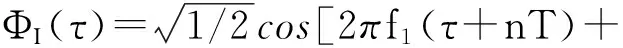

2 CPM倾斜相位的实现
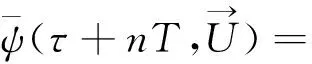
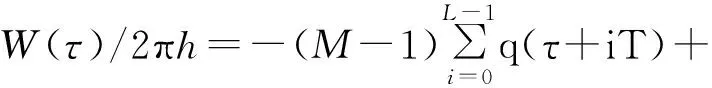
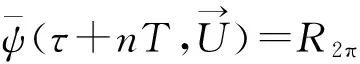
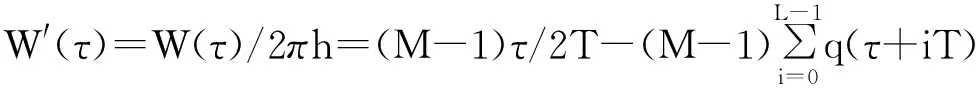
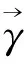
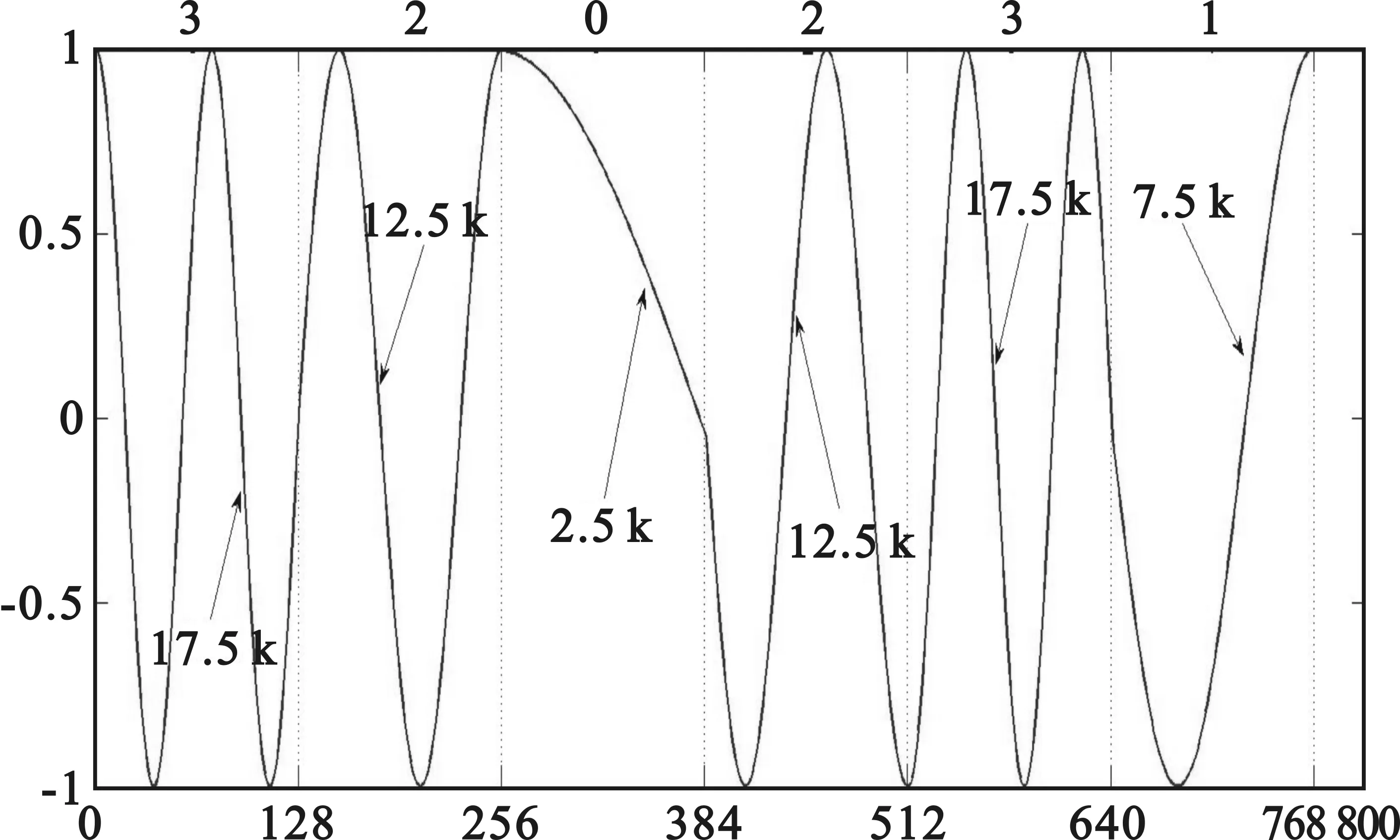
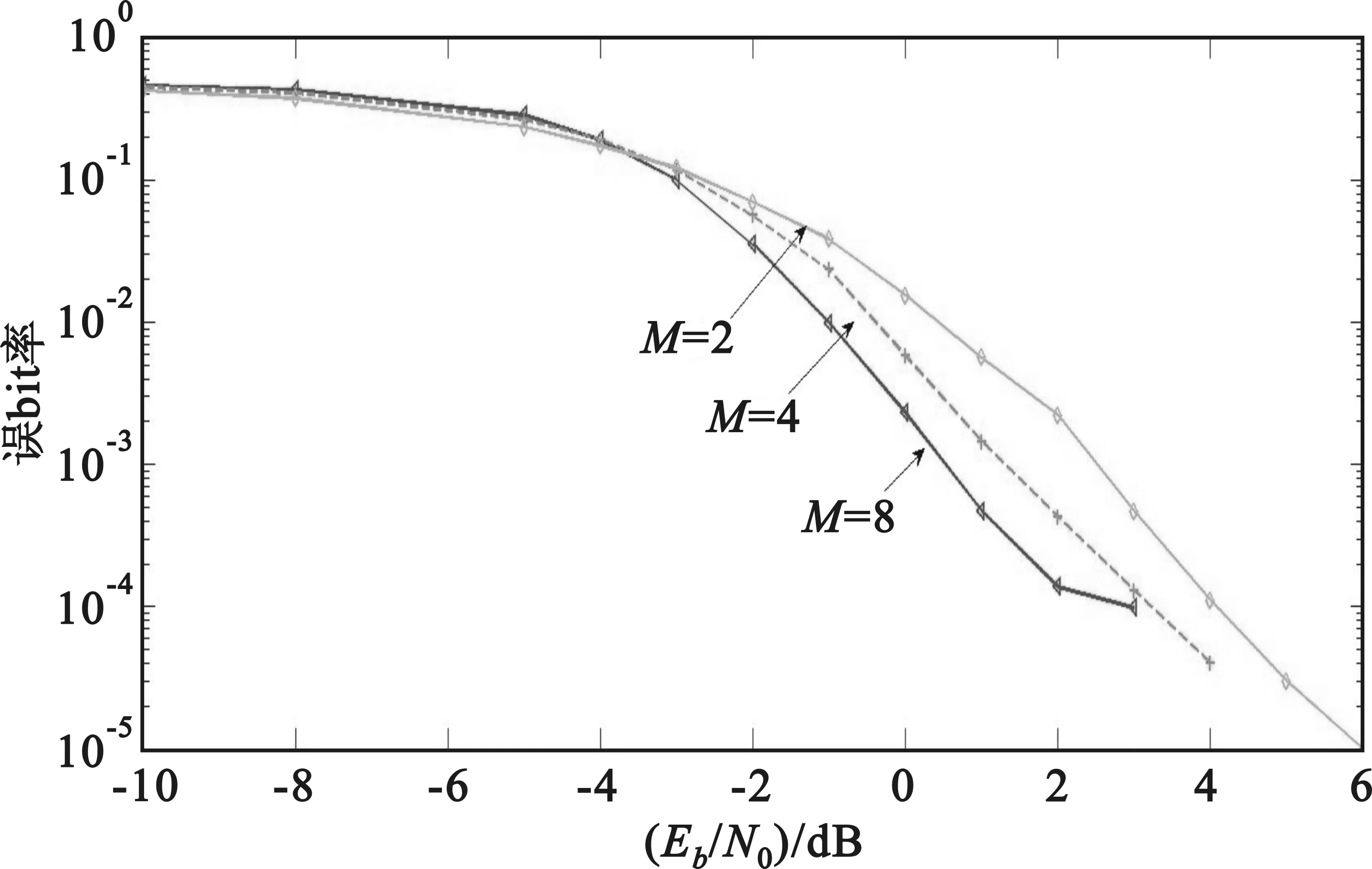
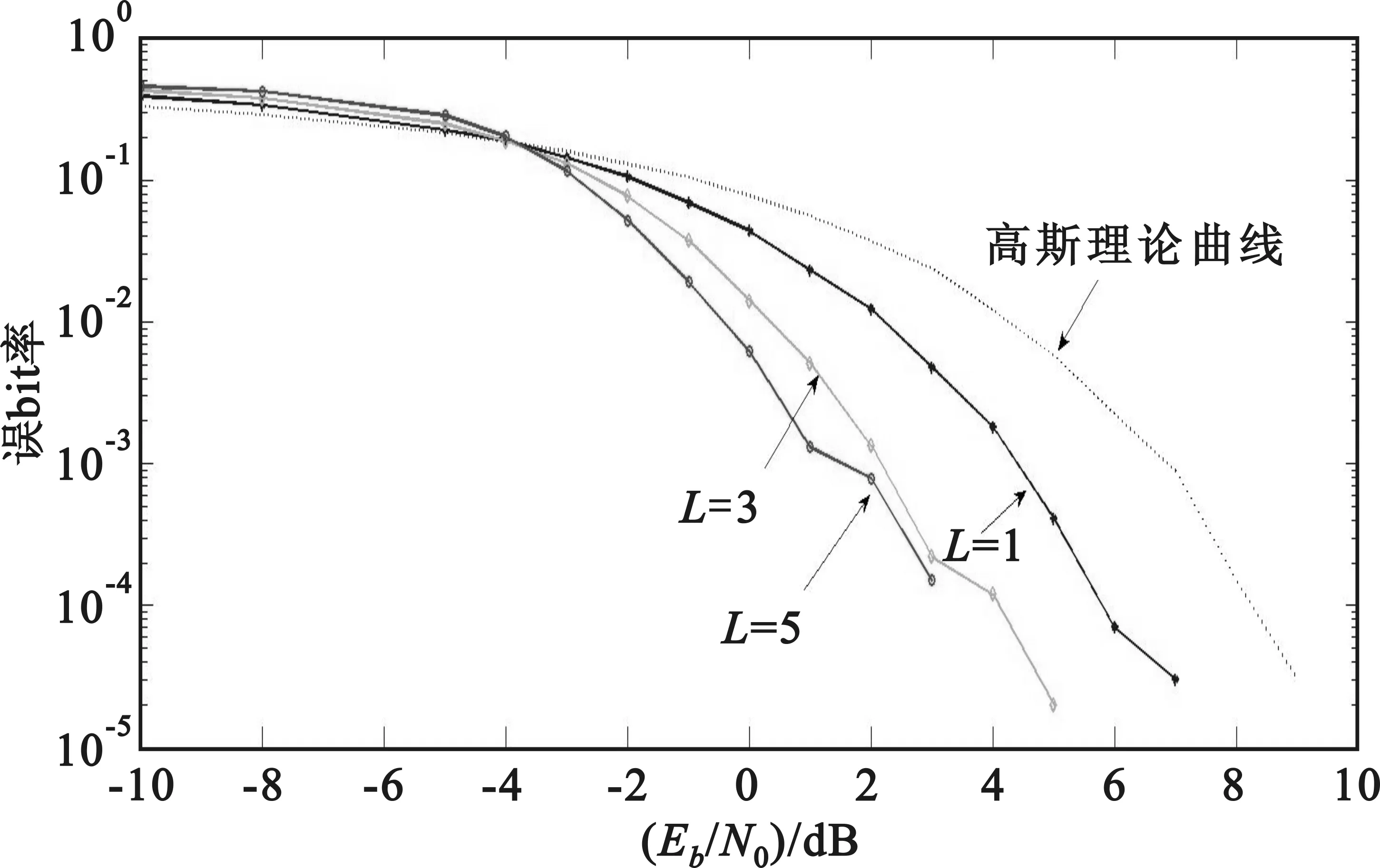
3 CPM倾斜相位的实现

4 结 语

