大地电磁测深三维反演系统及应用
2015-02-24张昆何钰娴严加永
张昆, 何钰娴, 严加永
(1. 中国地质科学院矿产资源研究所,国土资源部成矿作用和资源评价重点实验室,北京 100037;
2. 国家地质实验测试中心,北京 100037)
大地电磁测深三维反演系统及应用
张昆1, 何钰娴2, 严加永1
(1. 中国地质科学院矿产资源研究所,国土资源部成矿作用和资源评价重点实验室,北京100037;
2. 国家地质实验测试中心,北京100037)
摘要:大地电磁测深是基于电磁感应原理,在地表采集正交的电、磁场来研究地壳乃至上地幔电性结构的地球物理方法,后期衍生出采集高频天然场信号的音频大地电磁测深和采集人工源信号的可控源大地电磁法。此类方法在深部构造研究、矿产资源勘查、油气资源探测等多领域得到了广泛应用。近几年来,虽然其野外工作趋近三维勘探水平,但其采集数据的处理和三维反演研究仍然存在不足,限制了地质解释的准确度和效率。针对这些问题,我们开发了大地电磁测深的三维反演软件系统,系统主要分为静位移校正、三维反演的初始模型构建和三维反演3个模块,有效地解决了数据处理中的静位移问题和数据解释中的三维反演问题,并且其中涉及的很多算法改进了现有技术,在计算精度、计算效率和成本节约方面有很大优势,具有良好的应用前景。
关键词:大地电磁测深;三维反演系统;静位移校正;模型构建
1大地电磁测深原理
大地电磁测深法(MT)是基于电磁感应原理以天然电磁场为场源,在地表测量相互正交的电场和磁场来研究地壳和上地幔电性分布的地球物理方法。它以天然交变电磁场为场源,当交变电磁场以博得形式在地下介质中传播时,由于电磁感应作用,地面电磁场的观测值将包含地下介质电阻率分布的信息。而且,由于电磁场的集肤效应,不同周期的电磁场信号具有不同的穿透深度,因此,研究大地对天然电磁场的频率响应,可以获得地下不同深度介质电阻率分布的信息。研究大地电磁场对了解地球内部信息有着重要的作用。
在20世纪50年代初期,卡尼亚(Cagniard) 提出了在平面电磁波场中水平均匀层状介质的大地电磁法初始模型,研究了标量阻抗的计算方法,开创了电磁测深研究的先河。然而地球的层状介质模型假设与实际的地球模型相差很远,不能很好地解决实际地质问题。60年代中后期大地电磁法在理论上取得了一些重大的进展,考虑到了地球各向异性以及二维、三维等地下介质的不均匀性,建立了大地电磁场张量阻抗的概念及相应的数据处理方法、技术[1]。例如,坎特韦尔(Cantwell)提出考虑多维介质的张量阻抗估算方法,斯维福特(Swift)、 莫尔森(Morrison)、西姆斯(Sims)、沃扎夫(Vozzof) 等相继研究了张量阻抗的性质、分析方法和计算过程[1]。70年代以后随着计算技术的发展,国内外对大地电磁理论方法进行了深入研究,提出了各种一维及二维正反演方法、三维正演计算、场的影响及改正方法。并且,针对大地电磁法场源的随机性和天然电磁场信号的不足,提出了音频大地电磁法(AMT)和可控源大地电磁法(CSAMT)。总的来说,大地电磁测深及衍生方法基本分为两部分,野外数据采集和室内资料处理解释,而数据处理解释主要包含阻抗估算、去噪、静位移校正、正反演计算等[2]。
大地电磁测深主要用于解决基于导电性差异的结构和构造研究,主要是[3]:研究沉积表层的层理和各项异性,确定结晶基底和变质基底的深度,估计在研究地壳和上地幔时沉积表层的屏蔽影响; 建立固结地壳上部(高电阻)的地电模型,估计孔隙度和渗透性,分出异常导电的(特别是石墨化的)地带; 估计在比较深的(导电良好的)地壳层位上流质的含量; 研究海洋地壳层理; 研究海洋和大陆的软流圈的导电性,估计局部溶化的程度; 建立全球的地幔导电率模型; 圈定矿体矿脉的范围和走向,大体确定矿体深度,为有电磁差异的矿藏开发作前期准备;寻找地下水走向及深度。
由于MT具有工作效率高、勘探深度范围大、垂向分辨能力、水平方向分辨能力高、地形影响小、高阻层的屏蔽作用小等特点,很快在深部构造、油气探查、地震预报、地热、煤田探测、固体矿产深部找矿、水文、工程、环境地质、海洋地质调查等得到广泛应用,对它的研究也越来越深入。
2三维反演研究现状
目前,大地电磁测深(MT)资料的三维正、反演问题,已成为国际地球内部电磁感应领域研究的前沿课题。国外从20 世纪70 年代中期,就有关于三维电磁正演模拟的研究。随着有限差分法、有限元法、积分方程法、边界元法等应用,MT 二维、三维模拟和反演都取得了长足的发展。近年来,随着计算机内存和速度的倍增,在三维正演方面的研究已趋于成熟,交错网格有限差分法成为主导的计算方法;随着三维正演的发展,MT 的三维反演研究也日趋升温,反演方法众多,主要有共轭梯度法极大似然反演、非线性共轭梯度反演、拟线性近似反演、快速松弛反演、贝叶斯统计反演和人工神经网络反演等。
而随着MT三维正演理论的发展,首先出现了积分方程法(Integral Equation, IE),由于其快速的计算效率,曾经引起许多学者的关注,使三维大地电磁模拟算法取得巨大的进步,在 90 年代初期,IE成为比较其他方法的标准。直到20世纪末,史密斯(Smith)于1996年提出了一种带有超低频阻抗校正的三维交错网格有限差分迭代算法,用以模拟三维大地电磁场分量[4,5],成为之后大地电磁场三维正、反演研究的重要基础。此外,谭捍东等系统论述了大地电磁三维交错网格有限差分数值模拟算法的实现过程,改进了正演算法,提出了简洁的边界条件[6]。徐凯军等用积分方程法实现了均匀半空间三维大地电磁响应的数值模拟。
在三维反演方面,史密斯和布克(Booker)提出了快速松弛算法(Rapid Relaxation Inversion,简称 RRI),通过解一个近似一维的反问题来计算在每个测点下面的电阻率扰动,把大地电磁三维反演问题转化为一维反演问题以提高计算效率[7],却降低了计算精度。麦克(Mackie)和马登(Madden)将共轭梯度算法(Conjugate Gradient Inversion,简称 CGI)引入大地电磁场的三维反演中,通过极大似然反演公式使模型响应和观测数据之间不同的方差权重之和达到极小化[8],是一种计算效率较高的算法,但是收敛速度较慢。此外,在OCCAM法基础上,将反演问题从模型空间转换到数据空间的反演算法[9]虽然在一定程度上提高了反演速度,但是对计算机CPU和内存的要求很高。纽曼(Newman)首先实现了阻抗资料的三维非线性共轭梯度并行反演,并首先发表论文,通过线性搜索和预处理代替求解目标函数的二次导数,大大地减少了计算时间[10],但基于网格节点的并行结构可能对计算精度有较大影响。谭捍东等实现了求最小构造的三维快速松弛反演算法[11],并成功对日本Kayabe地区实测资料和新疆土屋铜矿床MT资料进行了反演计算。林昌洪等在麦克和马登所做工作的基础上,实现了阻抗资料的三维共轭梯度反演算法,并对日本Kayabe地区实测资料进行了反演计算[2]。
3三维反演系统开发
针对数据处理解释中的静位移校正和反演两个部分,大地电磁测深三维反演系统主要包括三维初始模型构建、静位移校正和三维反演等功能模块。
3.1 三维静位移校正
小的、浅部不均匀体可能会产生不同于MT记录频段内所有频率相对应的随机响应[12],这些小地质体使得电阻率测深曲线在对数坐标上沿垂直频率轴方向产生明显的平行移动[13],相位曲线保持不变的随机响应被称为 MT 的静态偏移效应[14]。这一现象的产生主要是由于地表浅部二维和三维不均匀体边界的积累电荷所产生的二次电场[15]的作用[16]。
前人对静位移效应的校正方法的研究工作主要分为5类:空间滤波法[13]、表层不均匀体计算法、综合资料解释法[17]、独立测量校正法[18]、相位改正方法[17]。但现有方法的不通用性以及改正结果的不确定性,并且,这些方法都是基于大地电磁场二维理论发展而来的,没有将更为准确的三维大地电磁场理论应用于静位移的研究中,而是仅在三维测量等实际应用上提到了三维空间概念。
因此,大地电磁测深三维反演系统以静位移的三维理论和实测数据为基础,通过定量分析大地电磁场的实测高频数据(视电阻率和阻抗相位),判断是否存在静位移,并依托任意维度的反演计算校正静位移。该静位移校正方法为计算机自动处理技术[19],避免了额外的野外工作和室内处理工作,将静位移校正成本降为0,并且具有较好的校正效果,如图1所示。
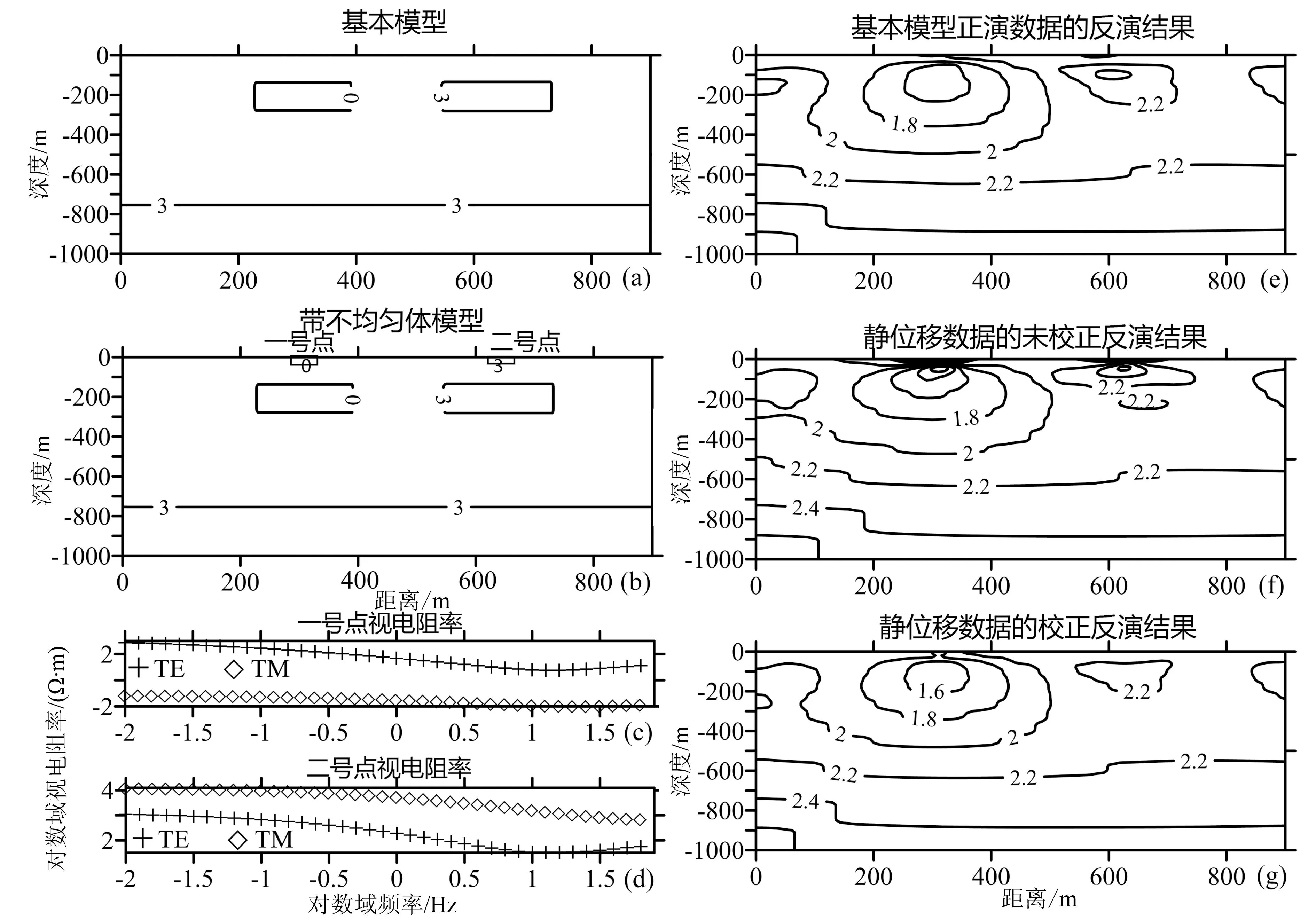
图1 静位移校正方法的理论验证示例
由理论合成模型(图1-a、b)模拟得到的正、反演结果(图1-e、f、g)可见,当浅表存在不均匀体时,地表测点存在静位移现象(图1-c、d),通过三维反演系统采用的静位移校正方法处理得到的数据更为接近真实的电磁场响应,其反演结果(图1-g)与正常数据的反演结果(图1-e)十分相似,而未校正静位移的数据反演结果与正常结果相差较大,对地下异常体的反映不准确。
3.2 三维初始模型构建
大地电磁场三维正、反演的计算量巨大,以往技术的反演计算消耗时间基本以“天”为计量单位,效率较低。而且,间接反演是目前使用的主流方法,此类算法需要首先建立初始模型,才能够进行反演计算,而目前的现有算法对初始模型具有一定的依赖性,初始模型的构建对反演结果的准确性有一定的影响。因此,需要设计一种初始模型构建方法在提高反演计算精度的条件下,同时提高计算效率。此时低维度反演成为解决这一问题的有效手段。
大地电磁测深数据的一维或二维反演具有很高的计算效率和一定的计算精度(准确性),因此,使用一维或二维反演结果作为三维反演的初始模型,能够在三维反演计算之初便较好地拟合实测数据,能够在很大程度上减少反演的迭代次数和计算时间,此外,一维或二维反演结果具备一定的准确性和合理性,能够辅助三维反演达到更高的计算精度和准确性。
因此,大地电磁测深三维反演系统以大地电磁场一维和二维正反演、三维插值和“印模”理论为基础,使用一维或二维反演结果构建三维反演初始模型的框架;基于低维度反演结果,通过三维距离差值重构三维反演初始模型;通过“印模”法修正模型,从而构建最优的三维反演初始模型[20]。
由图2可见,一维反演模型的三维插值结果(图2-a)较为粗糙,与层状理论合成模型有一定的出入,但以其结果作为三维反演的初始模型得到的三维电阻率模型基本上呈现出倾斜层状结构,电性分布与理论合成模型基本一致。此外,该大规模网格算例中均匀背景作为初始模型的三维反演迭代次数约50次,计算时间约8小时,但是用一维反演结果作为初始模型的三维反演迭代次数为15次,计算时间约2小时,大幅提高了计算效率。
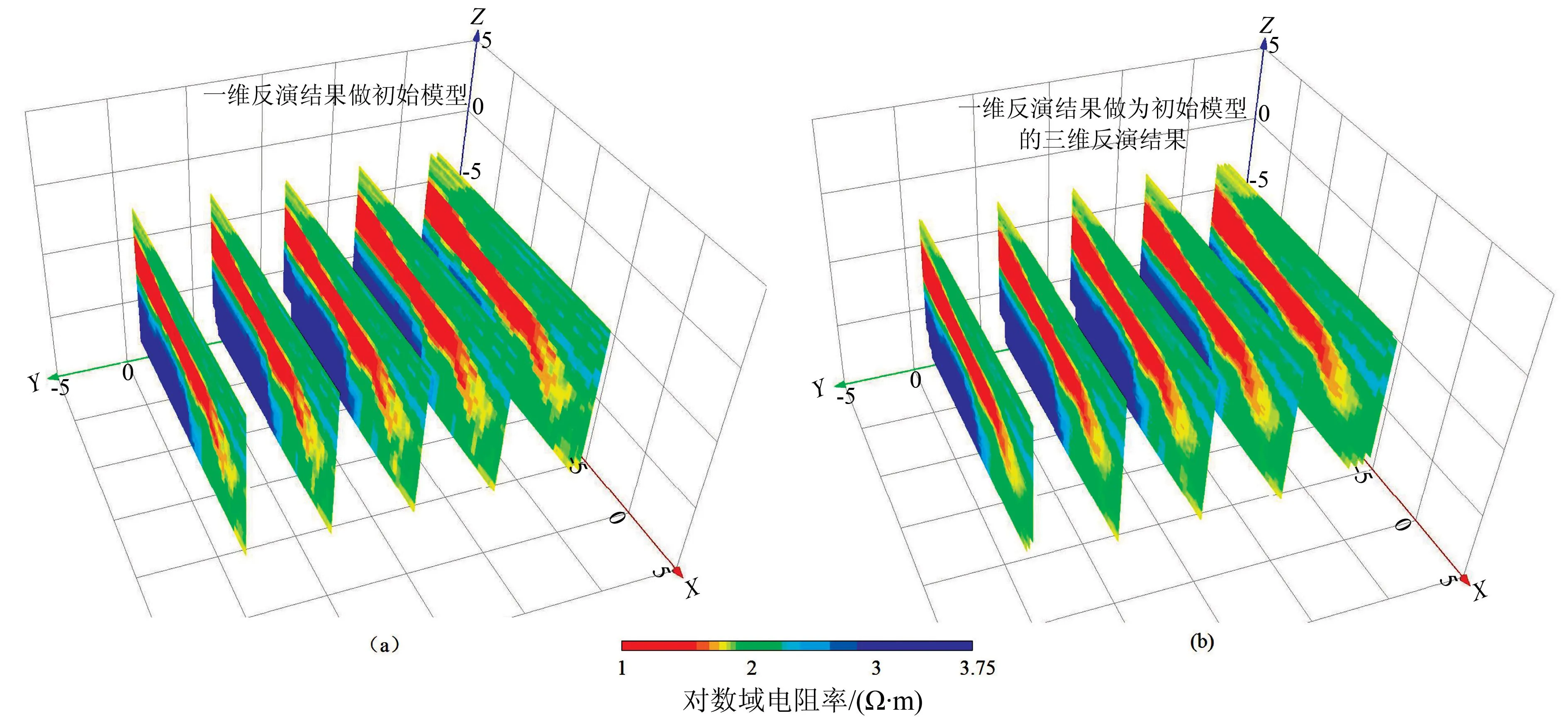
图2 初始模型构建及反演结果对比
3.3 三维反演
近年来,大地电磁测深资料的三维反演问题一直是国际地球内部电性结构研究的前沿课题。大地电磁数据三维反演,由于数据量和计算量大,对计算机硬件资源的要求高,并且需要花费大量的计算时间。但国内对大地电磁场正、反演的研究工作滞后,对三维正、反演问题的研究工作开展相对较少,国内目前还缺乏一种高效的、能够适用于普通计算机的且便于推广的、准确反映地下三维电性结构的反演方法。而我国大地电磁测深的工作量较大,很多工作已经达到三维勘探标准,如此庞大的数据量需要在较短时间内进行反演解释,在时间和经济成本上存在着很大的问题。
因此,大地电磁测深三维反演系统用预处理非线性共轭梯度方法构建三维MT反演问题[21, 22],在总结前人工作成果[4, 5, 10]的基础上,改进了现有的三维反演技术,提出了新的预处理因子。此外,系统优化了反演算法,添加了并行计算构架,大幅减少了对计算机硬件资源的占用率和计算时间,使得大地电磁测深数据的三维反演能够顺利的从大型服务器推广到普通计算机,乃至笔记本电脑。而计算时间由以往的“天”计量单位缩减到“分钟”,计算效果如图所示[23]。
图3为安徽泥河铁矿三维反演电阻率模型(图3-b、c、d),反演使用的数据为EH4采集的AMT阻抗数据,共使用测点224个,每个测点的使用频点2~10个,网格设置为30×36×40,迭代次数为79次,反演计算时间约90 min,最终拟合差为8.24。可见,四层电性结构与地质钻孔信息完全符合,并且圈定了侵入岩隆起部位,即为赋矿部位。
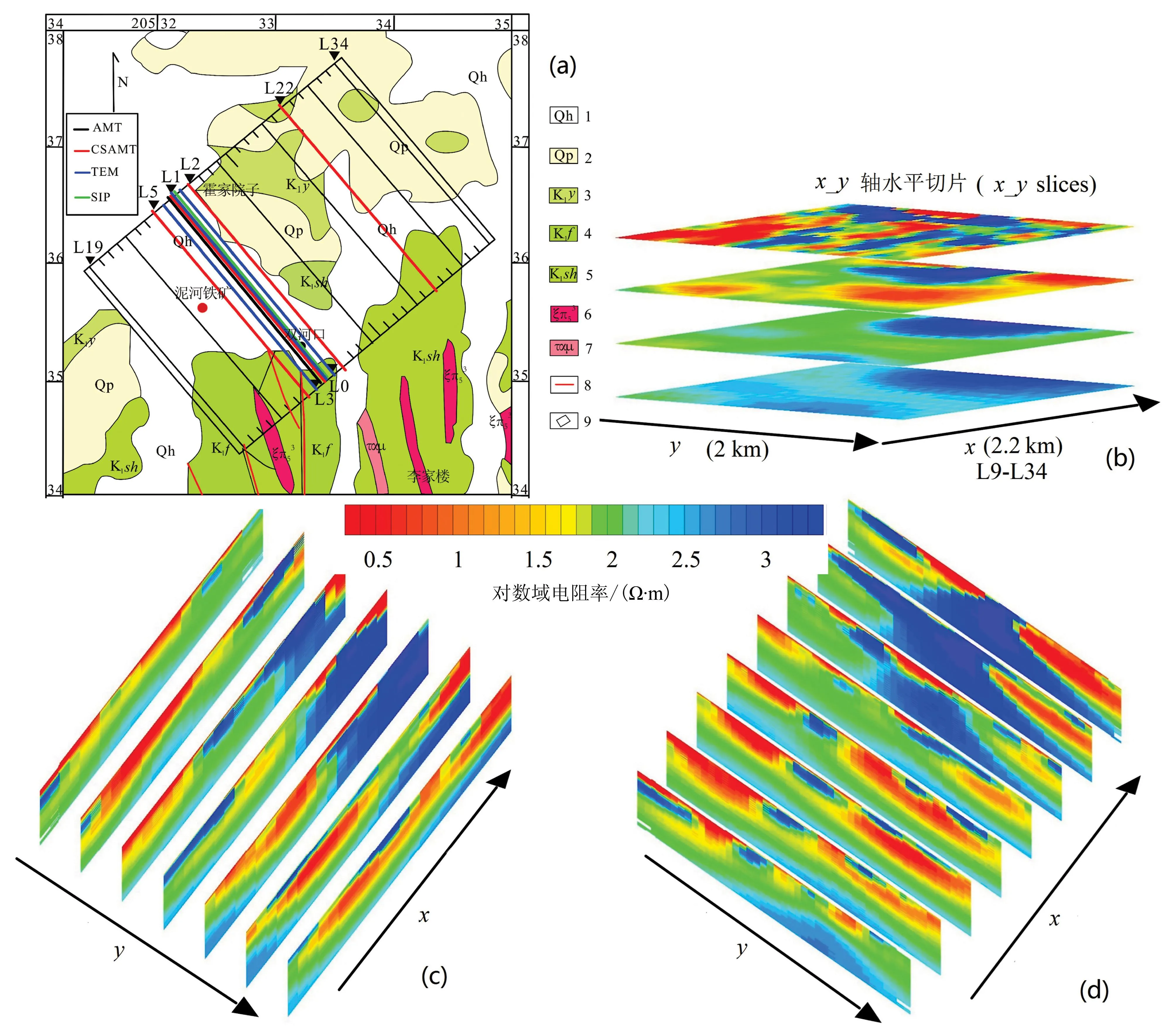
图3安徽泥河铁矿三维反演电阻率模型[23]
Fig.3The 3D resistivity inversion model of Nihe iron deposit in Anhu[23]
1. 全新统; 2. 更新统; 3. 杨湾组; 4. 浮山组; 5. 双庙组; 6. 正长斑岩; 7. 粗安玢岩; 8. 断裂; 9. 研究区
4结语
(1) 大地电磁测深的三维反演系统虽然仅涉及大地电磁测深、音频大地电磁测深和可控源音频大地电磁测深勘探工作中的数据处理解释部分,但具有较高的技术水平,在计算效率和计算精度上较以往技术有一定提高。此外,系统中涉及的静位移校正方法为独有的原创技术,在校正效果和节约成本方面有较大优势。
(2) 应用实例表明,本系统反演的地下电性结果与已知情况吻合较好,说明其具有较高的反演精度。当前,地调项目中设置了大量的大地电磁测深工作,但缺乏有效的反演软件,严重制约了该方法的应用效果。本系统的成功开发,可为地调项目中的大地电磁数据的反演、解释提供支撑,具有良好的应用前景和推广价值。
(3)但该系统目前还处于试用阶段,各个模块还没有有机的整合起来,目前仍然缺少一个优化的人机交互界面控制系统的操作,需要进一步完善图形界面,以方便地质工作者使用。
参考文献:
[1]严家斌.大地电磁信号处理理论及方法研究[D].湖南长沙:中南大学,2003.
[2]林昌洪.大地电磁张量阻抗三维共轭梯度反演研究[D].北京:中国地质大学(北京), 2009.
[3]石应骏. 大地电磁测深法教程[M].北京:地震出版社,1985.
[4]Smith J T.Conservative modeling of 3-D electromagnetic fields, Part I: Properties and error analysis[J]. Geophysics, 1996, 61: 1308-1318.
[5]Smith J T.Conservative modeling of 3-D electromagnetic fields, Part II: Biconjugate gradient solution and an accelerator[J]. Geophysics, 1996,61: 1319-1324.
[6]谭捍东,余钦范,Booker J,等.大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2003, 46: 5.
[7]Smith J T,Booker J R. Rapid inversion of two- and three- dimensional magnetotelluric data[J]. Journal of Geophys Research, 1991, 96: 3905-3922.
[8]Mackie R L,Madden T R. Three-dimensional magnetotelluric inversion using conjugate gradients[J].Geophysics Jonrnal International, 1993, 115: 215-229.
[9]Siripunvaraporna W,Egbert G. Three-dimensional magnetotelluric inversion: data-space method[J]. Physics of the Earth and Planetary Interiors, 2005, 150: 3-14.
[10]Newman G A,Alumbaugh D L.Three-dimensional magnetotellutric inversion using non-linear conjugate gradients[J]. Geophys J Int, 2000,410:424.
[11]谭捍东,余钦范,魏文博. 大地电磁法三维快速松弛反演[J]. 地球物理学报, 2003, 46(6):850-855.
[12]Swift C M. A magnetotelluric investigation of an electrical conductivity anomaly in the southwestern United States[D].cambridge:M I T, 1967:48-67.
[13]Berdichevsky M N,Vanyan L L,Kuznetsov V A,et al.Geoelectric model of the Baikal region[J]. Physics of the Earth and Planetary Interiors, 1980, 22: 1-11.
[14]Pellerin L,Hohmann G W. Transient electromagnetic inversion :A remedy for magnetotelluric static shifts[J]. Geophysics, 1990, 55: 1242-1250.
[15]Torres-Verdin C,Bostick F X.Principles of spatial surface electric field filtering in magnetotellurics[J]. Geophysics, 1992, 57: 603-622.
[16]Park S K,Orange A S,Madden T R.Effects of three-dimensional structure on magnetotelluric sounding curves[J]. Geophysics, 1983, 48: 1402-1405.
[17]Berdichevsky M N, Dmitriev V I. Distortions of magnetic and electrical fields by near-surface lateral inhomogeneities[J]. Acta Geodaet Geophys, 1976, 11: 447-483.
[18]Andrieux P,Wightman W E. The so-called static correction in magnetotelluric measurements[M]. Georgia,Atlanta,United States:54th Annual International Meeting SEG, 1984: 43-44.
[19]张昆.用于大地电磁场静位移校正的模型设计软件[P].中国人民共和国国家版权局, 2014:2014SR009601.
[20]张昆.基于一维反演的大地电磁场三维反演初始模型设计软件[P].中国人民共和国国家版权局, 2013:2013SR160125.
[21]张昆.大地电磁场非线性共轭梯度三维反演软件 [P].中国人民共和国国家版权局, 2012: 2012SR057553.
[22]张昆,董浩,严加永,等.一种并行的大地电磁场非线性共轭梯度三维反演方法[J].地球物理学报, 2013, 56(11):3902-3911.
[23]张昆,严加永,吕庆田,等. 安徽泥河玢岩铁矿电磁法探测试验[J]. 地质学报, 2014, 88(4):496-506.
3D Inversion System of Magnetotelluric Sounding and its Application
ZHANG Kun1, HE Yu-xian2, YAN Jia-yong1
(1.InstituteofMineralResources,ChineseAcademyofGeologicalSciences,MLRKeyLaboratoryofMetallogenyandMineral
Assessment,Beijing100037,China; 2.NationalResearchCenterforGeoanalysis,ChineseAcademyofGeological
Sciences,Beijing100037,China)
Abstract:Magnetotelluric is a geophysics exploration method for studying the crust and upper mantle electrical structure, which measures the surface orthogonal electric and magnetic fields based on the electromagnetic induction and natural electromagnetic fields. Thereafter, the audio-frequency magnetotelluric method which collects the high frequency domain of natural field and controlled source audio-freguency magnetotelluric method which collects artificial source are derived. These methods are widely used in deep structure study, mineral resources exploration, oil and gas exploration, and so on. Though the field work achieves 3D level in recent years, 3D data processing and inversion are insufficient and the efficiency and accuracy of interpretation is limited. To solve these problems, we develop the 3D inversion system of magnetotelluric sounding which contains static shift correction, initial model design and 3D inversion. The system effectively solves the static shift of data process and 3D inversion problem. A lot of algorithms in the system are improved which have advantages on calculation accuracy, efficiency and cost savings. And the system has a good application prospect.
Key words:magnetotelluric sounding; 3D inversion system; static shift correction; model design
作者简介:张昆(1983—),博士,助理研究员,主要从事电磁测深方法研究。Email:zhangkun1010@163.com。
基金项目:中央级公益性行业专项“大地电磁场静位移效应机理分析与校正方法探索(编号:K1318)”和中国地质调查“破碎蚀变岩型金矿深部找矿勘查技术集成(编号:12120114053301)”项目联合资助。
收稿日期:2014-10-08; 改回日期: 2014-12-05。
中图分类号:P631
文献标志码:A
文章编号:2095-8706(2015)01-0025-06
