基于FPGA的误差校正神经网络算法设计与实现
2015-02-23朱承
朱承
(重庆电子工程职业学院,重庆401331)
基于FPGA的误差校正神经网络算法设计与实现
朱承*
(重庆电子工程职业学院,重庆401331)
摘要:为了能够在真实硬件平台上进行实现,对原有的误差校正构造性神经网络算法进行了优化,并对优化后的误差修正算法进行了FPGA设计与实现。提出算法通过在自动生成一个合适的神经架构的同时对二个参数进行设置来提高算法性能。对这种算法实现的所有步骤进行了全面的描述并利用两种基准问题对结果进行了深入分析。结果显示,与标准的基于个人计算机(PC)的实现相比,提出的神经网络算法FPGA实现在计算速度方面有着明显的提高,由此证明了FPGA在误差校正算法神经计算任务中的实用性及适用性。
关键词:FPGA;构造型神经网络(CoNN);误差校正;阈值网络
人工神经网络(ANN)是受大脑功能启发而得到的能够应用在聚类和分类问题上的数学模型,这种数学模型已在不少领域获得了成功应用,包括模式识别、股市预测、控制任务、医学诊断及预报。尽管已在ANN领域进行了多年研究,但为给定的问题选择一个合适的架构仍是一个艰巨的任务[1-2]。
在解决或缓解这一问题的几种策略中,随着对输入数据进行分析,构造型神经网络(CoNN)使网络的生成成为可能。由此这些网络能够与这组数据的复杂性相匹配。此外,对于CoNN中的训练程序在标准前馈神经网络中需要很大计算量的问题,可通过增加并行计算速度来解决。误差校正训练竞争型网络是最近提出[3]的一种CoNN算法,由于这种算法和大多数的CoNN的一样未冻结先前合并的神经元的突触权值,且包含有一个内置的用于避免过拟合问题的过滤方案,因此该算法能够允许神经元在整个训练过程中进行学习,从而实现竞争。该算法的这两个特点可使其生成具有良好泛化能力的紧奏型神经架构,从而更适合于应用在有限资源的设备上,如微控制器、嵌入式系统、传感器网络和FPGA[4]。
近几年,由于科技的进步,人们已构造出具有巨大的处理能力和记忆存储能力的FPGA,且这些FPGA已在一些领域(通信、机器人学、模式识别任务、架构监控等)得到应用[5-6]。由于FPGA属于内在并行设备且能够在神经网络模型中处理信息,因此更适用于神经网络的实现。一些研究已经分析了在FPGA中的神经网络模型的实现[7],根据FPGA是否包括片上学习过程,可完成对FPGA的粗分类[8]。片上学习实现中,神经网络模型的训练通常可在个人计算机(PC)上进行且只将突触权值传输到作为硬件加速器[9]的FPGA上。与此相反的是,片上学习实现[10]可使PC自主独立地训练模型,但这种方式在提供更强的灵活性和更高效率的同时将会消耗更多的FPGA资源。
因此本文对对原有的误差校正构造性神经网络算法进行了优化,并对优化后的误差修正算法进行了FPGA模块设计,最后在Virtex-5 FPGA平台进行了算法运行效果测试。本文的贡献主要有2点,首先对通过FPGA并行处理误差校正神经网络算法,可实现的速度优势进行了分析,其次是根据能够存储的最大模式数量对利用FPGA的实际局限、数据集的尺寸和使用定点表示法的区别等等进行了分析,特别是对实现一个真实硬件时的分析。最终证明了运用FPGA实现的误差修正神经网络算法应用,能够有效解决现实工业生产的问题。
1 优化的神经网络构造型算法
1.1构造神经网络算法原理
误差修正神经网络是一种新颖的神经网络构造型算法,这种算法利用神经元和修改的感知器学习规则之间的竞争,来构造对监督分类问题具有良好预测能力的单隐层紧凑架构。作为CoNN算法,误差修正神经网络能够在学习阶段在线生成网络拓扑,从而避免有关选择合适神经架构方面复杂问题的出现。与先前提出的构造型算法相比,误差修正神经网络的新颖之处在于位于单隐层中的神经元能够为学习输入数据而竞争,这一过程可允许紧奏型神经架构的创建。在单隐层中的神经元的二进制激活状态(S)取决于N输入信号ψi及N突触权值(wi)和偏差(b)的实际值,如下:
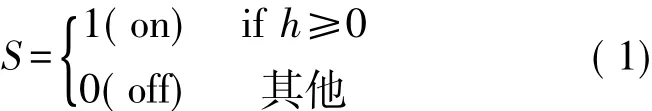
式中,h代表神经元的突触电位,可定义为
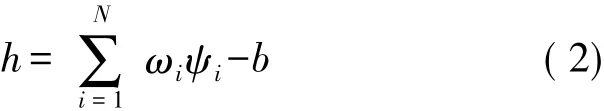
在热感知器规则中,根据下列的方程式可在线完成(在显示单输入模式后)对突触权值Δwi的修改,
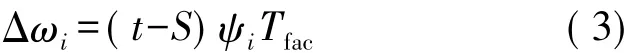

根据(5)可知,T值会随着学习过程的进展而减小。

式中,I代表界定误差修正神经网络算法在一个学习周期中迭代的循环计数,Imax代表允许迭代的最高次数。这种算法的一个学习周期指的是一个过程,这一过程从网络上显示出已选择的模式开始并在检查所有的神经元对输入做出正确回应后或在神经元的突触权值选择学习的实际模式后(无论是现有的还是新的神经元修改自身的突触权值)结束。
1.2优化参数设置
为了能够在真实硬件平台上进行实现,并提高算法的鲁棒性,以便在广泛的参数值范围内运行情况相当良好,需要对原有误差修正神经网络算法的2个参数进行设置。提出的算法优化的2个参数如下:
(1)gfac确定何时终止学习周期及向隐层中引进一个新神经元的增长因数。
(2)φ确定在何种情况下可认为输入实例是一种噪声并根据以下条件将其从训练数据集中移除。
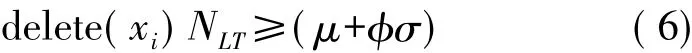
式中,xi代表一种输入模式,N代表在该数据集中模式总数,NLT代表模式xi在当前学习周期中显示在网络上的次数,μ和σ分别相当于该算法在一个学习周期中试图学习每种模式的分布平均值和方差。该学习过程开始于一个单隐层中的神经元及一个能够计算隐藏神经元响应的输出神经元。通过在网络中显示输入模式,可使该学习过程继续,如果误分类输入模式,在满足一些条件的情况下,当前的一个神经元(其输出与目标模式值不相匹配)则会进行学习过程,否则一个新的神经元将会进入该架构进行学习过程。在所有误分类输入模式的神经元中,只有当Tfac值大于该算法的gfac参数时,具有最大Tfac的神经元才能开始该学习过程,所包含的一个条件用于预防忘记学习先前存储的信息。如果未找到可满足这些条件的感知器,网络中将会增加一个新神经元并开始新的学习周期(该周期所有神经元的温度值均复位到T0),并在该新的学习周期结束时使
式中,t代表显示输入的目标值;ψ代表通过权值wi连接到输出的输入单元i的数值。与标准感知学习规则的区别在于热感器器包含有Tfac因数。该Tfac因数取决于突触电位的数值和人工引入的温度值(T),计算出的Tfac因数值在式(4)中显示。用噪声模式过滤程序式(6)。通过重复先前的步骤可使该算法继续进行迭代运算,直到网络完成对训练集中所有模式的正确分类。
2 FPGA设计
FPGA属于利用预制的逻辑块和程式化互联资源可重复进行编程的硅芯片。人们可对其进行配置使其实现自定义的硬件功能,在这种意义上,FPGA通过重新编译一个新的电路配置FPGA几乎可以实现对自身行为的实时改变。通过将FPGA资源分成3个主要部分可在Virtex 5 FPGA中实现误差修正神经网络算法。图1显示的是完成运算所必需的控制模块、模式模块和神经元模块及它们之间的结构图。我们在下面对3种块的组织进行了描述并在分段中对具体实现细节进行了评论。
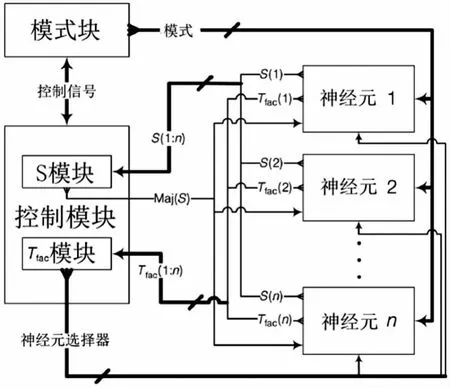
图1 FPGA设计的方案
2.1模式模块
模式模块可对培训模式进行管理。通过串行端口模式可接收到来自PC的突触权值并可将其存储在FPGA的分布式RAM块中。通过利用2n byte及n值可显示出模式。需注意的是每一种模式类(目标输出)均有一个备用的额外位。
在接收到来自控制模块的信号后再进行运算的期间,模式模块将会向所有的神经元发送一个随机选择的模式。为避免重复训练已给定的模式,可将最后一个发送模式的记忆位置切换至一个对应的最终符合条件的记忆位置,因此符合条件的记忆位置数量将会减少一个。由于这种情况牵涉到修改突触权值及开始新的学习周期,因此系统将会一直重复这种动作直至找到一种网络输出不同于其目标值的模式。
2.2神经元模块
每个神经元均由一组查找表(LUT)构成,该查找表包含有用于计算其输出(S)和Tfac值及修改其突触权值的所有信息。神经元接收来自模式模块与输入模式相关的信息并对其突触电位值h进行计算,以便于通过以下方程式获得神经元的输出:
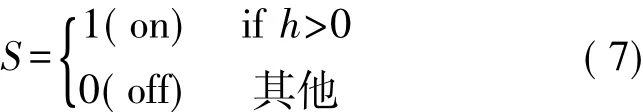
需注意的是该方程式与原误差修正神经网络方程式(1)相类似,但当前的这一方程式根据h值对是否激活神经元的的不平等条件进行了修改,因此现在仅当h>0时神经元才可处于激活状态,而在h=0时神经元将处于未激活状态。这种改变可以借助于一种更快的方法(见控制模块部分)对所有神经元(网络输出)的函数进行计算。通过神经元模块将所有隐藏神经元的S值发送到控制模块可计算出整个网络的输出值,这一输出值是返回到神经元中用于决定是否计算该数值(在网络输出与模式目标值不相匹配的情况下),或是否等待下一个输入模式(如果网络输出与模式目标值相匹配),以便于重新开始整个过程。在网络输出与当前模式的目标值不相匹配的情况下,每个神经元将计算各自的Tfac值式(4),并将该值发送到控制模块,控制模块则会返回有关具有最大Tfac值的神经元的信息,因此该神经元则会在其Tfac值大于gfac参数值的情况下修改自身的突触权值。代替使用RAM块,将突触权值存储在FPGA的寄存器中(这种方式可使突触权值接近于神经元)可减少有关设置方面问题的出现。
2.3控制模块
控制模块通过发送并处理来自神经元模块和模式模块的信息来组织整个信息过程。一旦将模式加载到模式模块中,控制模块将会接收到信号以便于开始执行算法。通过向模式模块发送信号指示其向神经元发送随机选择的模式可启动该算法过程。
误差修正神经网络是一种构造型ANN模型,其架构随着训练过程的进展而形成,而FPGA在进行编程前需要对所有的元件进行指定,在控制模块控制一个标示时,系统就已创造出在架构中神经元可能的最大数量,其数量决定了神经元是处于激活状态(包含在真实架构中)或处于未激活状态(等待潜在的包含)。在学习过程开始时,所有的突触权值设定为零且控制单元仅可以激活一个神经元。
当将随机选择的模式发送到神经元时,系统则会计算出它们的输出(S)且控制模块将会计算这些信号(整个网络输出对先前输入的响应)的函数,然后将输出值与目标值相比较,如果它们互相匹配,控制模块则会发送信号使其释放一个新模式;如果它们不相匹配,每个神经元将会得到一个Tfac值,以便于选择出最大的Tfac值,并且当Tfac值大于gfac参数值时,神经元则可以开始修改其突触权值,控制单元将会从神经元处接收到的Tfac值中选出错误的Tfac值及具有最大Tfac值的神经元。此时,控制模块将向已选出的神经元发送信号,这样该单元就能够对其突触权值进行修改。按照这一过程可连续完成对权值的修改并依照式(3),可对每个突触进行更新。
控制模块包括两个模块:Tfac模块和S(输出)模块。Tfac模块用于计算一组神经元的最大Tfac,然而S模块则用于计算S的函数。在以下部分中对这两种模块进行了详细的说明。
3 FPGA实现步骤
(1)S模块该模块用于计算隐藏神经元输出(S)的函数。图2显示的是有关该模块操作的示意图。首先添加隐藏神经元输出(Si)的然后该值将会与由步骤2划分的活跃神经元的数量相比较,由此可计算出函数。当激活的神经元的数量大于未激活的神经元的数量时,该模块的输出为“1”,否则该模块的输出则为“0”。对于该电路的逻辑运算,将正确的逻辑移位运算应用在活跃神经元上可获得一半数量的活跃神经元。由于在该控制模块上的计算不是同步的,因此仅在一个时钟周期内即可完成该模块的运算。
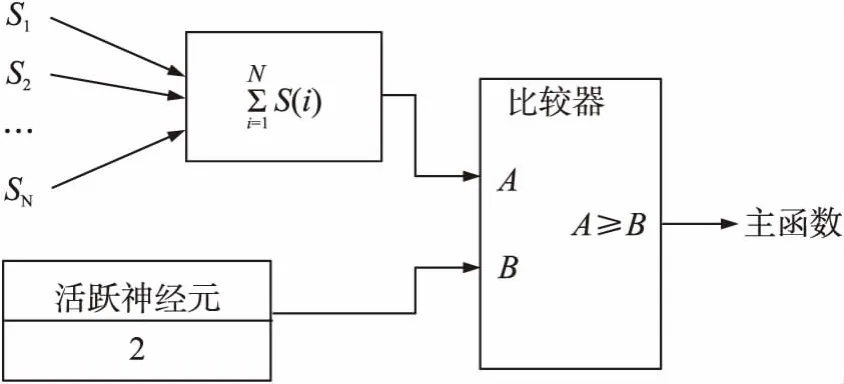
图2 用于计算隐藏神经元输出的函数的S模块功能图
(2)Tfac模块该模块负责计算出在当前模式下(“错误”神经元)输出与目标值不相匹配的所有神经元中最大的Tfac值。由于该模块能够更有效地计算出所有神经元的Tfac值,因此我们将“正确”神经元的Tfac值设定为0,以便于在所有神经元中获得最大的Tfac值(将不活跃的神经元的Tfac值也设定为0)。由于不需要使用最大的Tfac值来减少系统的运算频率,因此可在16个神经元模块中计算出最大的Tfac值。如果活跃神经元的数量超过16,系统将存储第1块获得的最大Tfac值并将其与第2块获得的最大Tfac值进行比较,然后存储目前得到的最大Tfac值。利用这种处理方式获得最大Tfac值直到分析完所有的活跃神经元。图3显示的是有关在误分类输入模式的神经元中寻找具有最大Tfac值的神经元的过程示意图。该图的左下方显示的是同步模块运算的时钟信号,该图的上方显示的是集合在被反复发送到逻辑电路中的16个神经元模块的Tfac值,利用逻辑电路可计算出该块最大的神经元数量,计算时需将目前得到的最大Tfac值考虑进去。分析完所有块后,Tfac模块将输出找到的最大值(最大Tfac值)和一个用于指示具有最大Tfac值的神经元的数值(索引)。
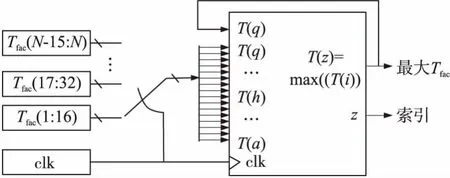
图3 用于计算活跃神经元中的最大Tfac值及获得该值的神经元的索引的模块功能图
(3)产品实现完成该算法需对几个产品进行计算,例如计算Tfac值,获得突触权值及神经元电位(h)。特别是计算Tfac值时需进行3个乘法运算:第1个与计算T有关,第2个与指数函数的插值有关,第3个则用于获得最终的Tfac值。每个神经元仅有一个能够用在时分复用方案中用于降低使用LUT次数的乘法器块。代替使用Xilinx特定的乘法器核心,我们使用了可输出的代码,以便于发挥其在其他FPGA上的潜在应用能力。本方案要求的LUT的数量与输入数据的位的大小成比例,例如对于两个分别具有Na和Nb个位的长度的矢量来说,其产品需要Na×Nb个LUT,因此其输出具有Na+Nb个位的大小。
(4)突触权值精度考虑到获取相对高的精度可能需要相对大的表达,突触权值的表达可以根据可利用的资源来选择,这将意味着每个神经元的LUT数目的增加(结果是可利用神经元数目的减少)与最大运算频率的降低。突触权值的精度非常重要,因此其结果值类似于通过使用浮点表示法(在基于PC代码中使用的)获得的数值。利用长度N1与N2带有整数和小数部分的位数组可表示出突触权值。N1用于确定-2(N1-1)到2(N1-1)可获得的最小值与最大值,而N2则用于确定精度2-N2。表达一定正值范围内所有可能的离散值所需的位数取决于间隔最大值与最小值的差异,根据下列方程式可获取所需的位数。
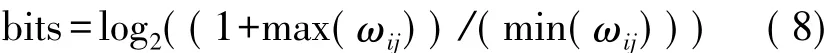
表1显示的是按照表达突触权值N1+N2所使用的位数(N1与N2分别表示该表达的整数与小数部分),需要的LUT数量、最大运算频率、可利用神经元的数量及精度。
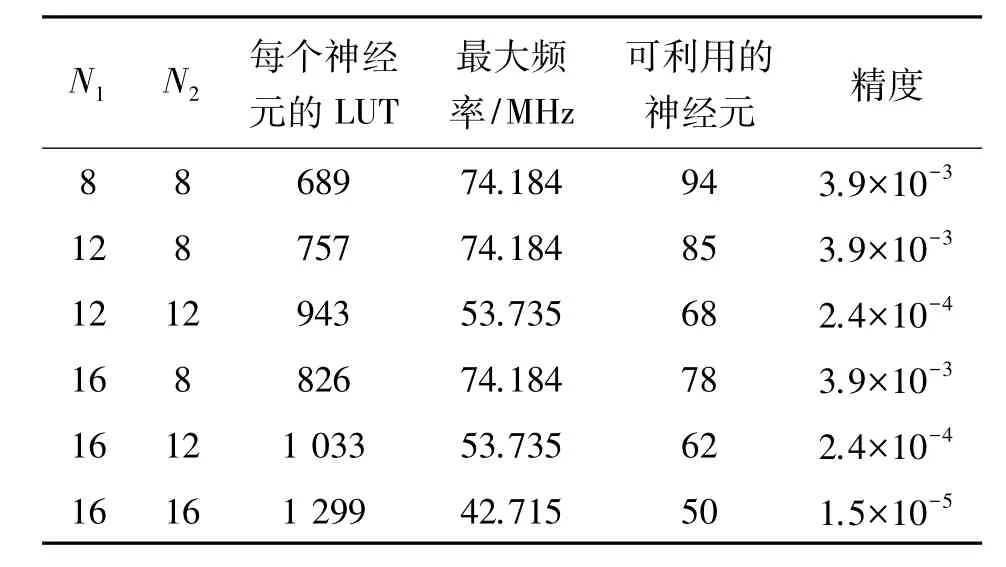
表1 N1和N2变化时LUT的数量、最大运算频率和可利用神经元的数量与精度
N1与N2分别表示整数与小数部分。
(5)输入数目误差修正神经网络网络中的输入数量是由训练模式的大小所决定。当输入大小从本质上修改每个神经元的LUT数量与能够被储存在记忆板中的训练模式的最大数量时,输入尺寸将极大影响整个FPGA的实现。而且,改变输入的数量还包括对程序代码的完全修改,从这层意义上而言,我们的方法是根据所需输入的最大数量来研发不同的代码。当然,非最佳选择就是在所有情况下均选择最大的输入代码,这无疑会降低板的其他能力。表2显示的是每个神经元的LUT数量、每1 024个模式所使用的随机存取存储(RAM)块的数量、可被储存的模式的最大数量(1 024×RAM块)及模式模块的LUT和寄存器的数量,这些均需以输入的数量为基础。由于剩余的输入用作输出分类,因此表中所示的输入大小与2的幂次方减1相对应。
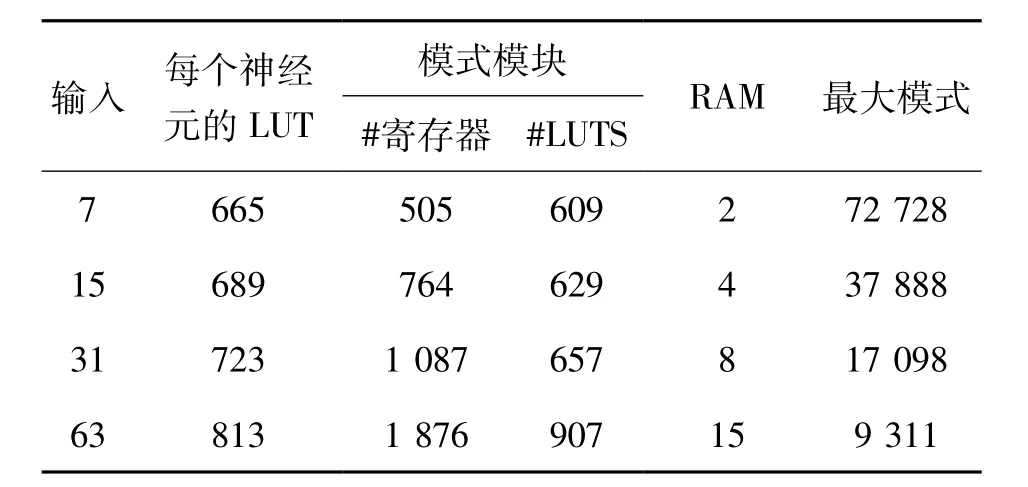
表2 每个神经元的各项参数值
(6)Imax对于原始的误差修正神经网络代码而言,对决定一个神经元在一个学习周期内所能经受的最多的学习修改次数的数值Imax进行了修改。若通过具有相关高计算费用的除法运算来利用该数值计算温度(T)值,则Imax就是数值2的有限幂次方,这将允许除法运算在正确逻辑移位上的转变。Imax的最大允许数值是217=131 072。
4 实际测试
目前实现所使用的开发板属于Virtex-5 FPGA评估平台。这种设备包括Xilinx Virtex-5 XC5VLX110T FPGA,它能够提供不同连接器装置:2个USB(主机和外围设备)端口、2个PS/2(键盘和鼠标)端口、RJ-45 (10/100/1000网络)和RS-232(male串行端口)连接器、2个声频输入(线路和微音器)、2个声频输出(线路、放大器和SPDIF)、视频输入、视频输出(DVI/VGA)及单端型和差分I/O扩展。表3显示的是Virtex-5 XC5VLX110T FPGA的一些特征,由此表明其具有的主要逻辑资源。图4显示的是Virtex-5 XC5VLX110T FPGA的图片。

表3 VIRTEX-5 XC5VLX110T FPGA的主要规格参数

图4 用于实现误差修正神经网络算法的Virtex-5 FPGA平台
在Xilinx ISE设计套件12.4环境下,采用硬件描述语言(VHDL)可对FPGA进行编程。我们的设计策略是避免使用特定的Xilinx核心,以便于从其他制造商处获得能够应用在FPGA上的总体设计。
我们已对选择的FPGA在VHDL中的实现与误差修正神经网络算法在C语言编程[11-12]中的实现进行了不同形式的比较,值得注意的是,在PC可用语言中,VHDL这种语言是最快的语言之一。运行C代码的CPU是英特尔(R)酷睿(TM)CPU四核Q6600@2.4 GHz。
使用一组16个单输出布尔函数来测试误差修正神经网络算法生成的速度与架构。测试所使用的函数包括两组算术逻辑单元(ALU)函数[13],即10个输入6 Alu2的函数与14个输入8 Alu4的函数。这两组函数都是从参照[14]的基准得来的,一并得到的还有输入2且3的互斥分离函数(XOR)。误差修正神经网络算法可在以下参数值下运行:gfac= 0.01与Imax=16 384(在以下情况下无需使用无噪音消除步骤,例如=∞)。此外,还可以使用一个锁相环块(PLL)将所有测试系统的频率设置为72.72 MHz。误差修正神经网络算法VHDL-FPGA与C-PC实现一组16个布尔函数学习时间的平均值与标准偏差,由图5中以对数函数y轴的形式可以显示出来。?
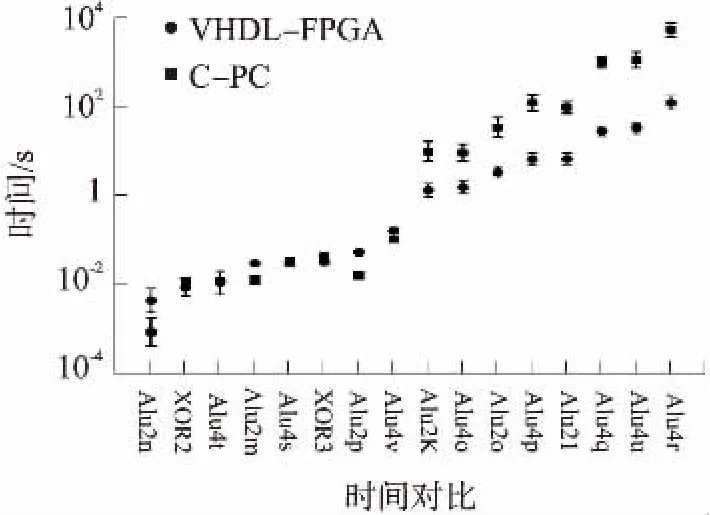
图5 误差修正神经网络算法VHDL-FPGA 与C-PC的平均值与标准偏差
我们进一步计算了随着建设性网络发展,新神经元加入有关的执行时间。通过输入10的函数Alu21比较FPGA所需的实现时间与基于PC的实现时间(重复30次以获取平均值)。图6(a)显示了实现FPGA与PC所需的时间,而图6(b)显示了两个平台之间的相对增长速度。图6(b)中的两条曲线与算法达到所示的神经元数目(累积)所需的相对时间一致。然而,当通过固定数量的神经元执行算法时,上方的曲线(每个神经元)就与对比相吻合。累积对比清楚地显示了FPGA的相对性能(与PC的实现相比)随着架构中神经元数目的增加而几乎呈现出线性增加。
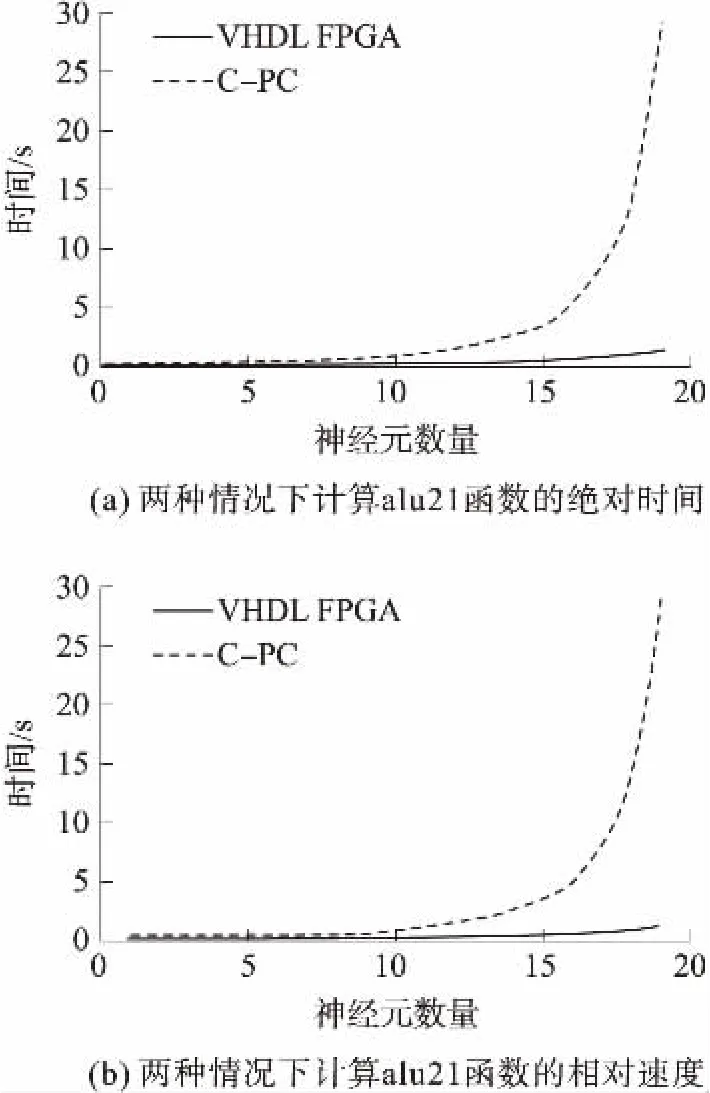
图6 计算alu21函数
在另一个实验中,我们使用一组8个二进制输出基准问题分析了现实函数的实现。表4显示了误差修正算法FPGA与PC的实现结果。表格的前两列显示了所使用基准问题的输入名称与数目。第3与第4列显示了实现FPGA与PC所获得的神经元数目,最后两列显示了FPGA与PC两种途径的泛化能力。利用10倍的训练/测试方案及下面的有关误差校正算法的参数(gfac= 0.1,Imax= 65 536,= 2)可计算出泛化能力。
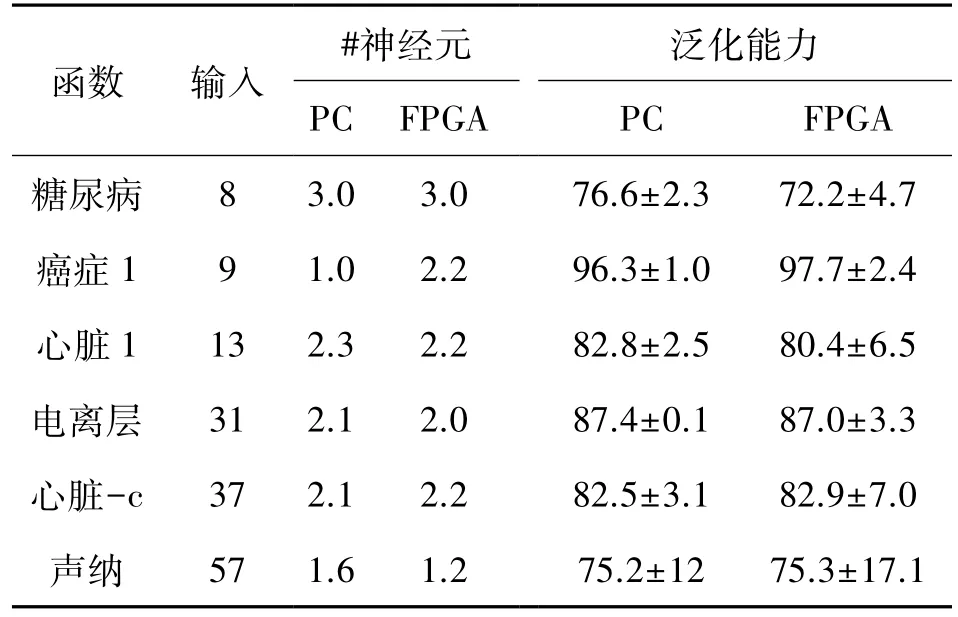
表4 8个基准问题在误差校正算法的FPGA版本中的实现结果
前两列显示函数输入的名称与数目,其余的几列显示了神经元的数目与使用两个平台所获得的泛化能力。
5 结论
在本文,我们已经分析并优化了原有的误差修正神经网络,并设计了相应的FPGA模块来实现神经网络构造型算法的片上学习。在众所周知的基准数据集(如表4)进行的一些测试显示,由于几乎难以对生成的架构的大小与该算法的泛化能力进行辨别,因此在大多数情况下,使用固定精度表达(16位定点)足以可得到与该算法的浮点原始基于PC实现的对比结果。
代替使用标准C语言的软件,该算法使用FPGA版本的优势在于:我们已观测到计算速度的显著提高。值得注意的是,随着问题复杂性的增加,该速度大致呈现出线性增长,因此在分析最复杂的函数的情况下(图5中Alu4r函数)即可获得增长高达47倍的因子。
根据观察到的结果,我们可以得出结论:测试结果证明了运用FPGA实现的误差修正神经网络算法应用,能够有效解决现实工业生产的问题,例如工业电机控制[15]、机器视觉[16]、工业控制网络、机器人学等。此外,实验证明了FPGA在已给定内在并行性处理的神经计算任务方面具有巨大的潜力。
参考文献:
[1]Monmasson E,Idkhajine L,Cirstea M,et al.FPGAs in Industrial Control Applications[J].IEEE Trans Ind Informat,2011,7(2):224-243.
[2]李利歌,阎保定,侯忠,等.基于FPGA的神经网络硬件可重构实现[J].河南科技大学学报:自然科学版,2009,30(1):37-40.
[3]Subirats J,Franco L,Jerez J.C-Mantec:A Novel Constructive Neural Etwork Algorithm Incorporating Competition between Neurons[J]Neural Netw,2012,(26)3:130-140.
[4]张荣华,王江.FPGA在生物神经系统模型仿真中的应用[J].计算机应用研究,2011,28(8):2949-2953.
[5]Hunter D,Yu H,Pukish M SⅢ,et al.Selection of Proper Neural Network Sizes and Architectures—A Comparative Study[J].IEEE Trans on Industrial Informatics,2012,8(2):228-240.
[6]张海燕,李欣.智能神经元网络前向传播过程的硬件实现[J].哈尔滨工程大学学报,2006,27(z1):40-45.
[7]汪光森,伍行键,李誉,等.基于FPGA的神经网络的硬件实现[J].电子技术应用,1999,25(12):23-25.
[8]杨银涛,汪海波,张志,等.基于FPGA的人工神经网络实现方法的研究[J].现代电子技术,2009,32(18):170-174.
[9]王炳健,刘上乾,汪大宝,等.基于FPGA的IRFPA非均匀性自适应校正算法实时实现[J].半导体光电,2008,29(4):583-585,589.
[10]李宏伟,吴庆祥.脉冲神经网络中神经元突触的硬件实现方案[J].计算机系统应用,2014,23(2):17-21.
[11]王建辉,崔维嘉,胡捍英,等.基于神经网络的鲁棒NLOS误差抑制算法[J].计算机工程,2011,37(24):7-9.
[12]刘新平,唐磊,金有海,等.扩展隐层的误差反传网络训练算法研究[J].计算机集成制造系统,2008,14(11):2284-2288.
[13]王正群,陈世福,陈兆乾,等.一种主动学习神经网络集成方法[J].计算机研究与发展,2005,42(3):375-380.
[14]齐明,邹继斌,胡建辉,等.神经网络在感应同步器零位误差补偿中的应用[J].中国电机工程学报,2008,28(9):105-110.
[15]胡煜.基于FPGA实现改进CORDIC算法研究[J].电子器件,2014(2):358-360.
[16]吴健,张志杰,王文廉,等.传感器动态误差高速并行修正方法及其FPGA实现[J].传感技术学报,2012,25(1):67-71.

朱 承(1974-),男,重庆人,硕士研究生,副教授。主要研究方向为电子信息技术,zczczc023@163.com。
The Design of FAT16 File System Based on MSP430F5529 and SD Card
XIA Lan1*,JIA Xiaodong1,QU Wenbo2
(1.School of Biological Sciences and Medical Engineering,Southeast University,Nanjing 210096,China;
2.Shanghai Rays Electronics Science and Technology Co.,Ltd.,Shanghai 201202,China)
Abstract:Aiming at the problem of the mass data produced by monitoring for a long time that cannot be stored,a FAT16 file system is designsed and developed based on low-power MSP430 MCU and SD card.Making use of SPI buses to communicate with the SD card,a FAT16 file system creats in the SD card,and samples and records the data in file.The data file can be recognized by Windows operating system and convenient for post data processing,this system has broad application prospects on the aspects of large-capacity data on site collection,memory and so on.The design can be used in protable ECG System,it has a high application value.
Key words:MSP430F5529; SD card; FAT16 file system; SPI; USB
doi:EEACC:1265P10.3969/j.issn.1005-9490.2015.04.045
收稿日期:2014-12-02修改日期:2014-01-05
中图分类号:TP391
文献标识码:A
文章编号:1005-9490(2015)04-0939-07
