一类基于径向基函数神经网络的离散混沌系统控制



一类基于径向基函数神经网络的离散混沌系统控制

刘庆丰，孙红磊

(兰州交通大学，甘肃 兰州730070)

摘要：以OGY法作为混沌控制策略对径向基函数(RBF)神经网络进行训练，通过参数扰动模型输出得到控制混沌运功的小扰动信号作为混沌控制器。并以Henon映射的混沌行为为基础进行仿真模拟，结果表明该方法的有效性。

关键词：OGY方法；RBF神经网络Henon映射；混沌控制

0引言

自H. Poincaré发现混沌以来，混沌学就成为了学术界的热点研究课题。由于混沌现象具有丰富的时空动态，能够不断的揭示人类社会与自然界之间存在的有序与无序的状态，从而不断的影响人们的生活和社会的发展。但事物往往具有两面性，由于混沌的不确定性，出现在系统中的混沌往往是有害的，因为系统的混沌运动蕴含着丰富的信息，但其吸引子内的轨线高度不稳定，变化万千，难以捕捉，因此不能准确的记录信息和识别系统，如不对其加以控制，根本无法使用[1]。为了使混沌为人类社会服务，如何控制混沌及将混沌研究成果由理论变为现实已成为当今面临的主要问题。基于此，笔者设计以OGY法为基础的径向基函数神经网络(RBF)控制混沌，通过K-均值聚类算法初始化RBF网络参数，然后利用K-最近邻近法和最小均方算法(LMS)对RBF输出层权值寻优及确定其宽度参数。并以Henon二维映射为例进行仿真实验，结果表明该方法的有效性。

1控制混沌

由于混沌系统具有对外部小扰动极度敏感的特性。以此OGY提出了严密而系统的参数扰动方法，通过在不动点的微小领域内使其局部线性化，同时不断的施加小参数扰动使其运动到规定的稳定轨道中，达到控制目的[2]。

设Poincaré映射为F，某一非线性动力学系统由式(1)描述：

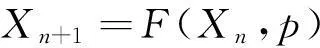
(1)

式中：Xn为系统状态向量，p为系统可调参数。

根据OGY法，用于控制不稳定周期轨道所施加扰动为：

(2)

式中：fu、λu分别为局部映射矩阵M=DXF(XF,p0)的可逆特征向量和特征值；DX表示F映射对状态向量X的导数；XF是F映射不动点；p0为可调参数初值，g≡DpF(XF,p0)是不动点随控制参数p变化而引起的变化量；Dp表示F映射对p的导数。

根据式(2)给混沌系统施加扰动作用，如果下次迭代落在不动点的稳定流形中，则以后的迭代都将被引到不动点，周期1轨道也会离开混沌吸引子而进入稳定周期轨道。本文神经网络训练以式(2)为依据，网络学习结束，则可将其当混沌控制器使用。控制系统框图如图1所示。

图1　RBF网络控制混沌系统学习框图

2RBF网络及其参数初始化

2.1　RBF网络及其原理

RBF神经网络是一个单隐层的前向神经网络，因其收敛速度快，全局搜索能力强，并能以任意精度逼近任意的非线性映射，并行分布处理信息及时等优点而越来越多的被人们所广泛采用。如图2所示其网络拓扑图，从网络结构上可以看出，它是由输入层、隐含层和输出层三层组成，其中输入层是由输入信号源节点x(i)组成。因为径向基函数是非线性的，所以，从输入层到隐含层的变换是非线性的，而隐含层的输出信号通过线性加权求值就变成了输出层节点的输出值，因此基函数隐含层空间到输出层空间的变换是线性的[3-5]。

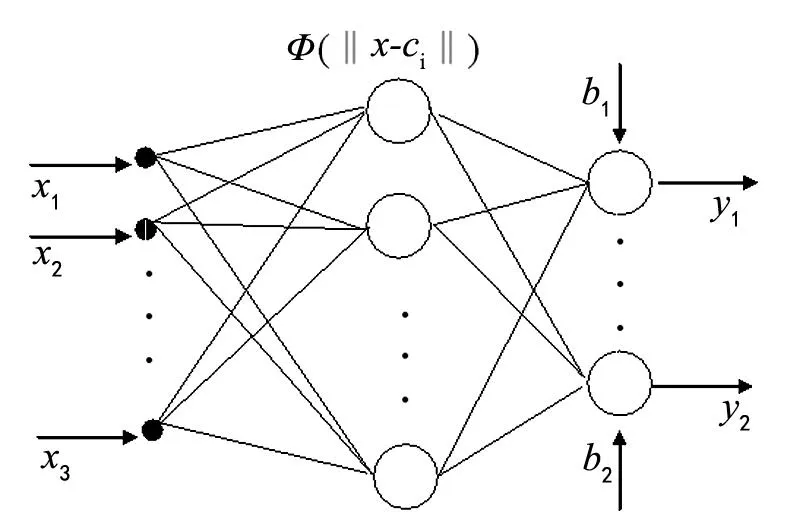
图2　RBF网络结构

在RBF神经网络中，某一维的网络输入输出关系可以采用径向基函数构造的映射f来表示，即:

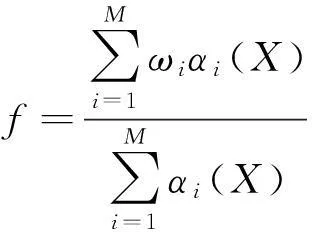
(3)

式中：M为隐含层的节点数；αi(X)为隐含层节点的基函数；ωi为网络的隐含层节点与输出层节点的链接权值；X为输入状态向量。

其中隐含层基函数为：

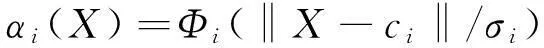
(4)

式中：ci是第i个基函数对应的中心点；σi是决定了该函数围绕中心的宽度；‖X-ci‖是向量X-ci的范数，它通常表示X和ci之间的距离；Φi是一个关于其中心成径向对称的函数，它在ci处有一个唯一的最大值，随着‖X-ci‖的不断增大，Φi迅速衰减，直至为零。因此对于给定的X∈Rn，只有靠近中心的一部分X的单元被激活，即当输入落在输入空间很小的指定区域时，隐单元才做出有意义的状态响应。

其中最常用的RBF基函数是高斯函数，即：

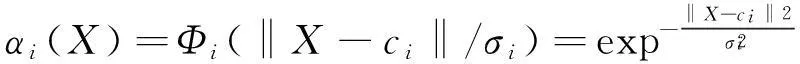
(5)

由前面所知，输入实现从X→αi(X)=Φi(‖X-ci‖/σi)=的非线性映射，输出层实现从αi(X)到y的线性加权映射，即。

2.2　RBF网络参数的初始化及其学习算法

由于对RBF神经网络的广泛应用及对它的研究，国内外学者已经提出了许多种训练神经网络的算法，如k-均值算法、梯度算法、BP算法、EM算法等。这些算法都是以训练RBF神经网络参数为目的的。文中，RBF神经网络隐含层节点选取高斯函数作为基函数，在其初始化时，需要确定三个参数：分别是第i个隐层单元基函数的中心ci、以及与之相对应的宽度σi和隐含层到输出层线性输出权矢量Wi。因为RBF神经网络具有自学能力(即调节权值和阈值)的特性，且它的学习算法主要包括无导师学习和有导师学习两部分。无导师学习也被称作非监督学习，即对所有输入的样本通过聚类算法进行聚类，以此来求得各隐层节点基函数的中心ci；而有导师学习也被称作监督学习，通过无导师学习得到隐层基函数中心ci后，因为隐含层到输出层的权值为一线性方程组，则可利用线性优化算法得到其输出权值Wi。

该设计用来控制混沌运动的RBF神经网络的学习过程分为三个阶段：利用k-均值算法确定隐层节点基函数中心ci、选择k-最近邻近值法得到其对应宽度σi、最后采用LMS算法优化输出层权值。

2.2.1k-均值算法确定隐层节点基函数中心ci

k-均值算法的主要思想是：在输入样本中随机选取k个样本作为RBF网络的初始聚类中心ci(i=1,2,…k)，之后将其他剩余输入样本放置到与之距离最近的第i个聚类中心，然后重新计算各类的训练样本，把重新算出来的平均值作为RBF网络的中心ci(i=1,2,…k)，直至隐含层的中心不变为止[6]。

其具体过程如下：

Step1：初始化聚类中心ci(i=1,2,…k)，通常是从输入样本Xj(j=1,2,…n)选取k个样本作为RBF神经网络的初始聚类中心；

Step2：将输入样本按照相邻最近距离的原则进行分配，即把输入样本Xj(j=1,2,…n)分配给聚类中心ci(i=1,2,…k)的聚类集合θj(j=1,2,…k),X∈θj，根据下式的原则进行分配：

dj=min‖Xj-ci‖(j=1,2,…n;i=1,2,…k)，其中dj表示输入的样本与聚类中心ci(i=1,2,…k)之间的最小距离。

Step3:计算每个聚类集合θj中所有样本的平均值，即为该类的聚类中心：

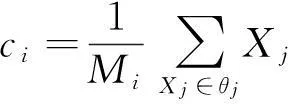
(6)

按照以上的步骤循环计算，直到每一个聚类中心ci(i=1,2,…k)的分布不再变化为止。

2.2.2k-最近邻近值法求宽度σi

运用k-最近邻近值法求解网络宽度，即第i个隐含层基函数的宽度是通过该中心到与其最近的k个中心的距离之和的平均值所决定的，可由式(7)求解：

(7)

式中：σi为第i个隐层神经元的宽度；cj是与第i个中心ci最邻近的中心，k是所选定的常数。

2.2.3LMS法得到输出层权值Wi

LMS的学习规则是使均方误差最小，使边界条件尽可能的远离分类模式，从而增加网络的抗噪能力。其学习规则的定义表达式如下：

(8)

式中：dr(n)为系统的期望输出；yr(n)为系统的实际输出，即：

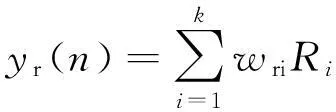
(9)

其目标是通过不断的调节权值，使mse从误差空间的某一点开始，沿着其斜面向下滑行，以使mse达到最小值。

具体推打过程如下：

Step1：初始化各连接权值wri，即赋给各个连接权一个较小的随机非零值；

Step2：输入训练样本，计算连接权值的调整量，其推导过程如下：

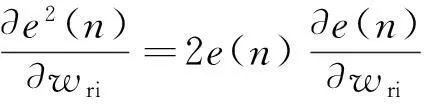
(10)

(11)

式中：Ri(n)表示第n次循环的第i个输入向量。则：

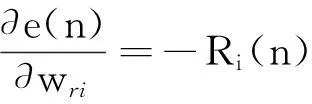
Step3：调整连接权值的表达式

根据负梯度下降的原则，网络权值的修正式(12)：

(12)

3Henon系统的动力学分析

对于Henon混沌系统的模型：

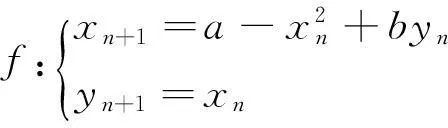
(13)

由其系统方程可得它的Jacobian矩阵行列式为：

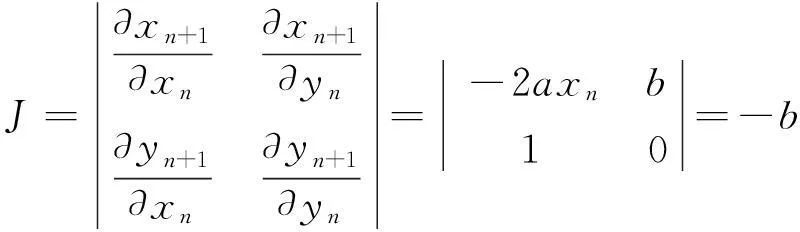
(14)

由其Jacobian矩阵行列式可得：

(1) 当b=0时，系统会发生退化现象，成为不可逆的一个一维混沌映射。

(2) 当b≠0时，则系统会成为可逆的一个二维混沌系统。若b为负值时，系统经过每次迭代之后其方向均会改变，且当|b|<1时，系统将是一个耗散系统，且每次迭代后其相平面(xn,yn)的面积变成为原来的|b|倍。

由不动点理论，可得Henon系统的不动点表达式为：

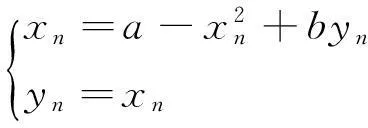
(15)

则可求得系统的两个不动点A,B,其中A,B坐标分别为：

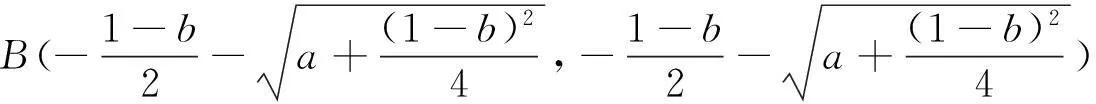
取a=1.4、b=0.3代入A,B两点坐标得到的系统的不动点坐标为A=(0.8839,0.8839)，B=(-1.5839,-1.5839)，并求出其对应的特征值和特征向量，其中不动点A=(0.8839,0.8839)处的特征值是λ1=0.1158，λ2=-2.5907，且其所对应的特征向量为(-1.924,1)，B所对应的特征向量为(0.1561,1)，由于A所对应的特征向量大于1，则A点是不稳定鞍点，且在A点附近形成了不稳定流形Ms，而B点的特征值向量的绝对值小于1，则在B点形成稳定流行M′s，通过Poincaré截面法，即稳定流形与不稳定流形相交，经过无穷多次迭代后，其点集{(xn,yn)}构成了一条不封闭的曲线，即图3为Henon系统的吸引子的Poincaré相图，通过MATLAB数值模拟迭代可得到。

混沌系统的内部结构如果不稳定，并且混沌系统具有初值敏感性，如果给系统任何小扰动都会使系统的拓扑结构改变以致使其动力学行为发生变化，致使其运动形态发生变化，将这种行为称为分岔现象。经过MATLAB数值模拟可得该系统的分岔图，如图4。

图4是变化参数a在区间[0,1.4]的分岔图，从图4中可得出，当系统在参数a=0.36时开始第一次倍化分岔，当a=0.9时系统发生第二次倍化分岔，且发现当参数a逐渐增大时，系统的分岔现象越来越复杂，且其间隔时间也越来越短，最后成为了混沌状态。则可发现Henon系统是典型的倍周期分岔系统。

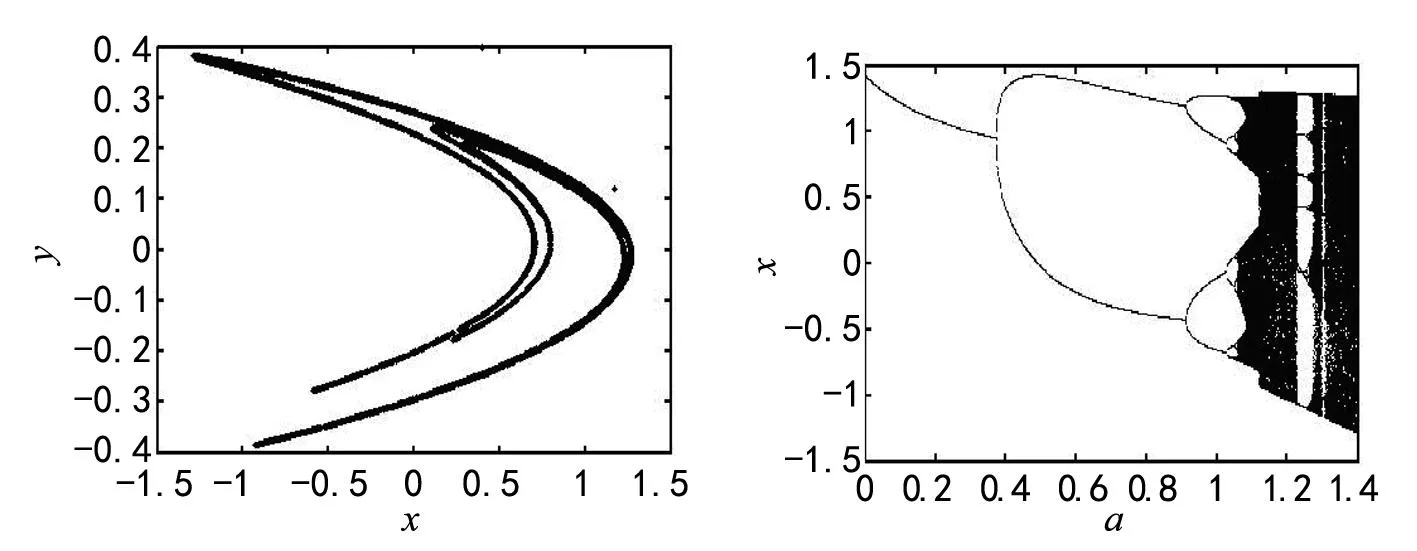
图3　　Henon系统的Poincaré　　　图4　　Henon系统的　　　相图　　　　　　　　　分岔图

Lyapunov指数谱是来判定动力系统是否稳定的重要指数。它是系统相邻的两条相轨线的平均收敛程度的一种度量。 对于Henon二维映射，应用Lyapunov指数λa,λb来描述。在系统的吸引子吸引域内任取一点作为一条轨道的起始点，并在该点的周围选择另一点作为另一条轨道的起始点。当轨道间距很小时，每次迭代所产生的间距变化会成指数型变化，若初时刻的间距为d0，经过一次迭代后变为：

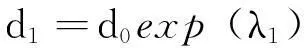
(16)

若系统的最大Lyapunov指数小于零时，系统处于不动点的稳定周期运动；当系统最大Lyapunov指数大于零时，系统将会出现混沌运动。通过数值模拟可得图5，发现Henon系统最大Lyapunov指数整体的变化趋势。

在此系统中，选择参数为a=1.4,b=0.3，可发现系统的最大Lyapunov指数为0.418，表明系统在此处于混沌运动状态。

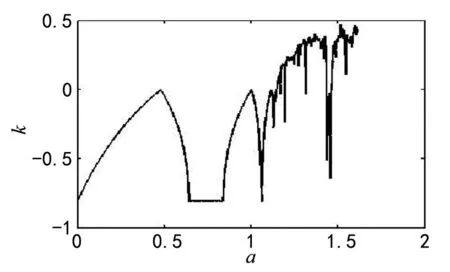
图5　Henon系统的最大Lyapunov指数图

4Henon系统的混沌控制[7-8]

由以上可知当a=1.4且b=0.3时系统发生混沌。由xn=a-x2n+bxn得其不动点(XF,YF)=(0.8839,-1.5839)因为|f1(XF)|>1，则XF为不稳定周期1轨道不动点。假设a是微扰a0变化的可调参数，令a=a0+p，则p即为式(17)的控制参数。(xF,yF)为p=0时的不稳定周期1的不动点。

(17)

其中ξn为：

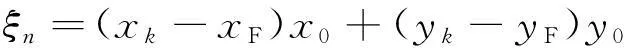
(18)

将式(18)代入式(17)并整理，得到施加在系统的扰动控制量为：

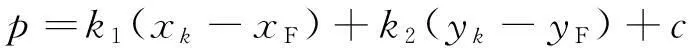
(19)

式中用以计算扰动控制的数据对为(xk,yk)，式(19)是标准OGY控制混沌方法的控制输入。即扰动量由(xk,yk)得出，采用径向基函数训练网络。将式(19)中的常数c合并到控制常数k1,k2中，于是，系统的总控制量为：

(20)

这里k1,k2可分别取为1.840,-0.30，式(20)中数据对(xk,yk)作为网络学习输入样本，网络实际输出pNNk再代入式(21)：

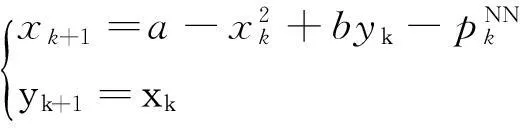
(21)

训练成功后，式(21)即为施加了控制作用的Henon映射。

通过RBF神经网络训练学习完成后，可将Henon系统混沌状态镇定道不动点处。其中图6是系统处于混沌的仿真曲线，图7是在迭代100步后加入RBF控制器，将系统的混沌状态镇定到不动点的仿真曲线。

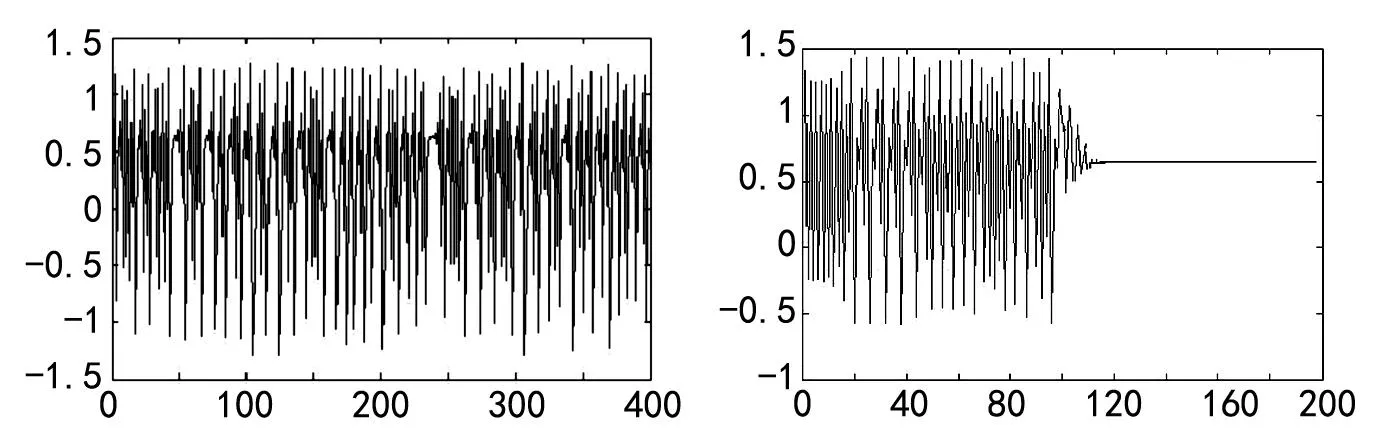
图6　Henon系统混沌状态仿真曲线　图7　100步后加入RBF控制器系统仿真曲线

5结语

以OGY法为基础，选取不稳定周期轨道中不动点周围的样本数据，并结合K-均值聚类算法、K-最近邻近法和LMS法训练RBF神经网络成为混沌控制器，并以Henon二维映射为例进行仿真实验，试验表明了该控制方法能够有效的镇定一类离散非线性混沌系统，并且响应速度快，从而表明该方法的有效性。

参考文献:

[1]杨绍普，曹庆杰，张伟.非线性动力学与控制的若干理论及应用[M].北京：科学出版社，2010.

[2]赵明成，朱洪波.OGY法控制Henon系统混沌的研究[J].机械，2010，39(10)：26-28.

[3]欧佳崎.基于RBF神经网络的混沌控制原理与永磁同步电机控制研究[D].长沙：长沙理工大学，2013.

[4]张 骅.优化算法改进的RBF神经网络在电动机控制中的应用[D].柳州：广西工学院，2010.

[5]曾喆昭.不确定混沌系统的径向基函数神经网络反馈补偿控制[J].物理学报，2013，62(3)：17-21.

[6]管硕，高军伟，张彬.基于K-均值聚类算法RBF神经网络交通流[J].青岛大学学报(工程技术版)，2014，29(2)：20-23.

[7]邰旭升.Henon混沌系统的控制与同步研究[D].西安：西安建筑科技大学，2010.

[8]刘金琨.机械系统RBF神经网络控制：设计、分析及MATLAB仿真[M].北京：清华大学出版社，2013.

Controlling Discrete Chaotic System Based on RBF Neural Networks

LIU Qing-feng, SUN Hong-lei

(LanzhouJiaotongUniversity,LanzhouGansu730030,China)

Abstract:The RBF neural network is trained by using OGY method as the chaos control strategy, and small disturbance signal of controlling the chaotic motion, which is obtained through the outputs of parameter perturbation model, is set as the chaotic controller. Meanwhile, the analogue simulation is carried out based on the chaotic behavior of Henon mapping, and the results show that the method is effective.

Key words:OGY method; RBF neural network; Henon map; chaos control

中图分类号:TP398

文献标志码：A

文章编号：1007-4414(2015)02-0157-04

作者简介：刘庆丰(1990-)，甘肃兰州人，在读硕士，研究方向：非线性系统动力学，车辆动力学。

收稿日期：2015-02-04