高高原机场飞行程序设计中的风螺旋线模型
2015-02-22范峥张飞桥张淼
范峥,张飞桥,张淼
(中国民用航空飞行学院空中交通管理学院,四川广汉618307)
高高原机场飞行程序设计中的风螺旋线模型
范峥,张飞桥,张淼
(中国民用航空飞行学院空中交通管理学院,四川广汉618307)
飞行程序是航空器根据飞行仪表和对障碍物保持规定的超障余度所进行的一系列预定的机动飞行,主要分为传统程序和PBN程序,其设计依据参照ICAO8168(PANS-OPS)[1]和美国终端区仪表程序(Federal Aviation Administration(FAA),Order 8260.3,United states standard for terminal instrument procedures(TERPS))。目前国内民航业发展处于井喷状态,随着拉萨机场、林芝机场、稻城亚丁机场、昌都机场的陆续通航,我国将成为拥有高高原机场最多的国家。
由于高高原机场的特殊性质,原有的风螺旋线模型不能真实刻画机场航线转弯保护区外边界。如何建立精确合理的高高原机场航线保护区,且安全高效利用有限空域资源,提高终端区容量,成为各方关注的焦点。本文参照有关标准,基于所获取的气象数据,通过分析已有的风螺旋线模型,探讨建立合适的转弯保护区外边界风螺旋线数学模型、风速模型,为高高原机场航线的转弯保护区的设计提供科学依据,以有利于提高复杂条件下航空器运行安全。
1风螺旋线数学模型建立
在程序设计中,转弯保护区是在标称转弯航迹周围考虑风速、航空器越障等因素设定的一块保护区域,其保护区外边界是考虑风速影响的风螺旋线[2],主要与转弯率R、转弯半径r、风偏移量Eθ有关。
通常风螺旋线源于转弯半径r,通过在理想飞行航迹之上增加风的影响得到Eθ,由此得到风螺旋线的数学模型为
ρ=r+Eθ
(1)
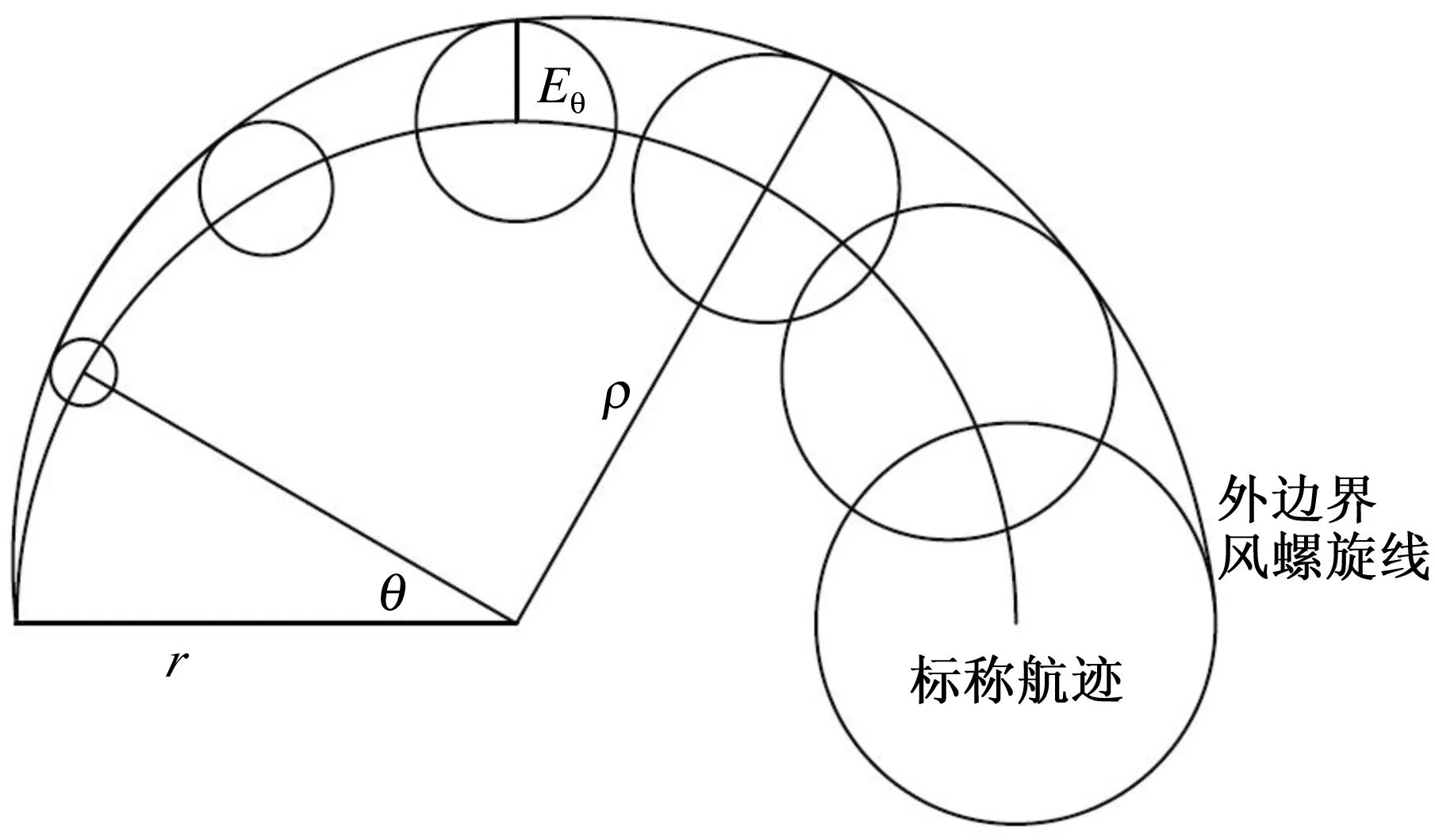
图1 风螺旋线的示意图
分析可知,转弯保护区的大小与W、VTAS、θ成正比。转弯时,假设VTAS不变,由于换算因数K值随高度升高而增加,导致VTAS随之变大,从而转弯保护区也变大。换算因数K可以通过查表得到,风速越大转弯保护区越大。因此,在设计转弯保护区时,必须获得精确的风速模型。
2风速模型的基本标准
根据ICAO8168(PANS-OPS),不同航段转弯保护区设计时考虑的风速模型有所不同,表1为ICAO风速模型。
一些发达国家已经根据本国的气象数据建立了更加符合本国实际情况的风速高度模型。与ICAO的风速模型相比,更加细化ICAO的标准,提高了运行安全和效率。法国和英国建立的风速模型见表2、3。

表1 ICAO风速模型

表2 法国建立的风速模型
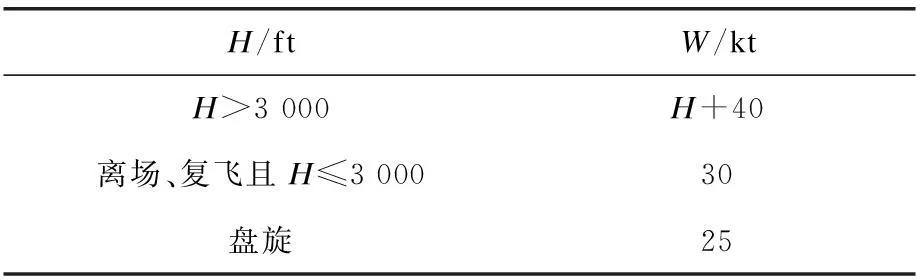
表3 英国建立的风速模型
现阶段我国采用ICAO标准,尽管能满足航空器运行安全,但高高原机场和处在强风带附近的机场,W、VTAS与ICAO标准存在差异,建立合理的风速模型[3]显得更加重要。
3风速与高度数学模型建立
收集某机场气象观测的数据,找出所有年份中月平均最大风速所对应的月份。比较该月份中每一高度层风速是否为最大值,是则保留,否则用最大风速值进行替换。
假设每一高度及其对应出现的最大观测风速作为一组实验数据(xi,yi)=(xi,f(xi)),i=0,1,…,m。分析相应离散点的分布,可以近似用某一函数s*(x)来表达。本文采用最佳平方逼近算法来求解近似函数s*(x)[4]。s*(x)为函数类Φ中的任意函数,Φ=span{φ0,φ1,φ2,…,φn}。
s*(x)可以写为

(2)
满足

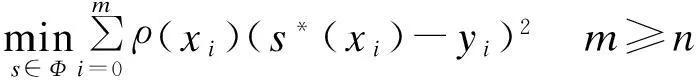
(3)
使得s*(x)满足式(3),令
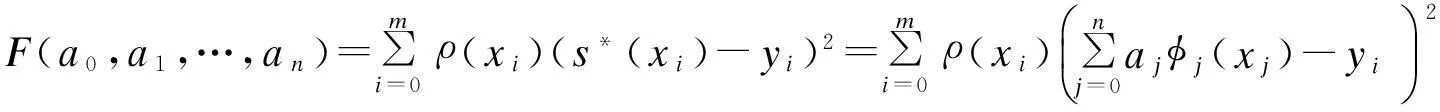
(4)

由式(4)得

(5)

最佳逼近函数求解结果参见图2。从飞行程序设计角度出发,保护区应考虑高度层上最大的风速,即拟合曲线应该包络这些离散的数据点。同时参照各风速模型的标准和简洁运用的原则,离散点的包络函数最佳为一次函数。结合上述因素考虑,本文采用对拟合函数求导数的办法和函数逼近的思想,求得最佳的一次分段包络函数。

图2 求解后函数图像
1)分析函数图形。在近地面至海拔7 000 m范围内,离散点的分布近似一条直线,直线斜率近似拟合函数在其凸点的导数为304,直线在x轴上的截距近似为15。在7 000~14 000 m范围内,离散点的分布杂乱无章,取正向偏离较大的点(离散点风速比拟合函数值大),其连线的直线斜率近似为拟合函数端点的斜率为598,直线在x轴上的截距近似为26。所以,粗略的一次分段包络函数模型为



图3 优化算法流程图
优化后,一次分段包络函数模型为

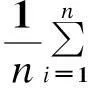

图4 优化前一次函数图像

图5 优化后一次函数图像
3)对优化后一次分段包络函数模型进行整理得到最终的风速高度模型为

ICAO风速模型、法国风速模型、英国风速模型、本文风速高度模型见图6。

图6 各种风速模型比较图
通过图像分析,相比其他风速模型,本文研究基于国内某机场的风速-高度模型更真实地反映出该机场周边风速随高度的变化,为该机场飞行程序设计及其转弯保护区的绘制提供了更为精确和可靠的依据。
4风螺旋线模型的优化比较
国内飞行程序设计辅助软件主要使用AutoCAD,其出色的绘图性能大大提高了程序设计的效率。而基于AutoLISP语言的二次开发使绘图更精确、简单。
基于风螺旋线数学模型式(1)和AutoLISP语言编写的Lisp程序[5],由计算机自动绘制出风螺旋线保护区的对比图,见图7。

图7 保护区外边界风螺旋线比较图
通过对图形的比较分析,基于本文所获得风螺旋线模型及考虑到转弯时飞机上升高度,所绘制出的转弯区外边界与ICAO风速模型下的转弯区外边界相比更加精确,减少了对空域资源的占用,更加符合该机场的实际运行。
5结语
精确的风螺旋线模型及符合实际运行的风速-高度模型精确刻画了净空条件复杂的机场和高高原机场的转弯保护区外边界风螺旋线,确保飞行安全的同时,提高了有限的空域资源利用率。
[参考文献]
[1]ICAO.Aircraft operations-construction of visual and instrument flight procedures(Doc8168)[S],2006.
[2]朱代武,何光勤.目视和仪表飞行程序设计[M].成都:西南交通大学出版社,2004:38-42.
[3]陈光亭,裘哲勇.数学建模[M].北京:高等教育出版社,2010:52-60.
[4]邵华平,何正友,覃征.几种函数逼近方式的逼近能力比较与综合[J].湖南师范大学自然科学学报,2003,26(4):22-26.
[5]郭秀娟,于全通,范小鸥.AutoLISP语言程序设计[M].北京:化工工业出版社,2008.
责任编辑:陈亮
摘要:标准的风螺旋线模型不能真实刻画高高原机场航线转弯保护区外边界。根据飞行程序对转弯区外边界的定义,提出并建立精确的风螺旋线模型,用最佳平方逼近算法探寻模型中风速与高度的关系,确立合适的风速高度模型并进行优化和对比。仿真图像表明:精确的风螺旋线模型使得转弯保护区设计更加科学可靠。在保证飞行安全的情况下,提高了有限的空域资源利用率。
关键词:高高原机场;飞行程序设计;风螺旋线;最佳平方逼近;AutoLISP
On Wind Spiral Model in Flight Procedure Design of High Plateau AirportFAN Zheng,ZHANG Feiqiao,ZHANG Miao
(College of Air Traffic Management,Civil Aviation Flight University of China,Guanghan 618307)
Abstract:A standard wind spiral model cannot simulate the outer boundary of a turning area in high plateau airport.Based on the definition of outer boundary of a turning area by flight procedures,this paper put forward and established a precise wind spiral model,exploring the relationship between wind speed and height by using the optimal square approximation algorithm,with an appropriate wind speed and height model finally established and optimized.The simulation images suggest that the precise wind spiral model can make the turning area design more scientific and reliable,and improve the airspace utilization rate while ensuring flight safety.
Key words:high plateau airport;flight procedure design;wind spiral;best square approximation;AutoLISP
中图分类号:V351.2
文献标志码:A
文章编号:1671-0436(2015)03-0031-04
作者简介:范峥(1990—),男,硕士研究生。
基金项目:中国民用航空飞行学院科研基金学生科技活动基金项目(X2013-38);国家科技重大专项课题(H3-8301-00-017)
收稿日期:2015-03-17
doi:10.3969/j.issn.1671-0436.2015.03.008
