折叠机翼的参数化气动弹性建模与颤振分析

倪迎鸽, 侯赤, 万小朋, 赵美英

(西北工业大学 航空学院, 陕西 西安　710072)

折叠机翼的参数化气动弹性建模与颤振分析

倪迎鸽, 侯赤, 万小朋, 赵美英

(西北工业大学 航空学院, 陕西 西安710072)

摘要：针对折叠机翼的特点建立了颤振分析的参数化气动弹性模型。参数化的结构模型基于模态综合法实现;参数化的气动力模型采用偶极子网格法建立;并且阐述了基于Gram矩阵范数对于气动弹性系统颤振边界的预测方法。以折叠机翼完全展开和完全折叠构型为例,将文中方法获得的颤振边界与特征值法获得的结果进行了对比,验证了该方法的正确性。通过对不同折叠角度下的颤振边界的分析可以得出:颤振边界对折叠角度很敏感;随着折叠角度的增加,颤振模态发生了变化;较高的结构模态阻尼比可以提高颤振速度,推迟颤振现象的发生。

关键词：折叠机翼；Gram矩阵；参数化模型；气动弹性；颤振

变体飞机可以根据不同的飞行任务改变构型,因此,受到了极大关注[1]。针对变体飞机的颤振问题,许多学者开展了广泛的研究[2-4]。与固定翼的颤振分析不同,折叠机翼因为折叠角的变化需要进行不同构型下的颤振分析。如果不采用参数化的建模方法,其颤振分析需要建立不同的结构模型与气动模型,显然,该过程是比较低效的。Zhao等[5]提出了参数化的气动弹性模型的建立方法,在MATLAB中实现了颤振分析。但在参数化过程中会遇到2个问题:①在不同的折叠角下,整个折叠机翼的质量矩阵和刚度矩阵会变为不对称的稀疏矩阵,此时采用MATLAB中eigs函数求解模态振型会出现求解问题,因为eigs函数要求质量矩阵为对称矩阵;若将稀疏矩阵转化为全矩阵,采用eig函数求解,又会出现数据的存储问题;②采用经典的颤振分析时,需要求解颤振特征方程的特征值,倘若对颤振特征值跟综失败,会出现“窜支”问题,从而得到错误的结果[6]。

随着以状态空间模型为基础的现代控制理论的发展,系统的稳定性也具有了成熟的理论可以借鉴。当气动弹性方程表示成时域的状态空间时,根据线性系统理论,当系统状态矩阵的全部特征值均位于复平面的左半部时,系统是稳定的,此结论为颤振发生的判定提供了依据。但特征值法的缺点是需要对不同速度下的系统特征值进行重复求解,当系统的维度较高时,特征值的求解比较费时,不便于工程应用。在现代控制理论中,Gram 矩阵具有广泛的应用[7-9]。最近,Bueno等[10]提出了气动弹性系统稳定性分析的新方法,该方法以Gram矩阵范数为基础,从能量的观点进一步阐述了颤振产生的机理,同时避免了对高维气动弹性系统特征值的求解,提高了计算效率。

本文采用模态综合法建立了折叠机翼的参数化结构模型,结合偶极子网格法建立了参数化气动力模型,并构建了气动弹性状态方程,采用Gram矩阵范数获得了折叠机翼的颤振边界;将折叠机翼完全展开和完全折叠2种构型的颤振边界与特征值法获得的结果进行了对比,验证了本文方法的正确性。本文方法不需要重复建立折叠机翼的结构和气动力模型,可以定性地确定颤振耦合的模态信息,提高了折叠机翼颤振分析的效率。

1参数化的气动弹性模型

折叠机翼结构由机身、内翼和外翼3个子结构组成,分别记为子结构A、B、C。本文将各个子结构简化为等厚度的铝板,在MSC.NASTRAN中采用CQUAD4单元来模拟,该单元的每个节点有6个自由度,即3个平动自由度ux、uy、uz以及3个转动自由度θx、θy、θz。对于连接处的每个界面节点,扭转弹簧耦合θx,MPC耦合其余5个自由度,实现了各个子结构的界面节点之间的铰链模拟。其中,子结构A与子结构B之间的扭转弹簧刚度为KA,子结构B与子结构C之间的扭转弹簧刚度为KB。折叠机翼在局部坐标下的有限元模型如图1所示。

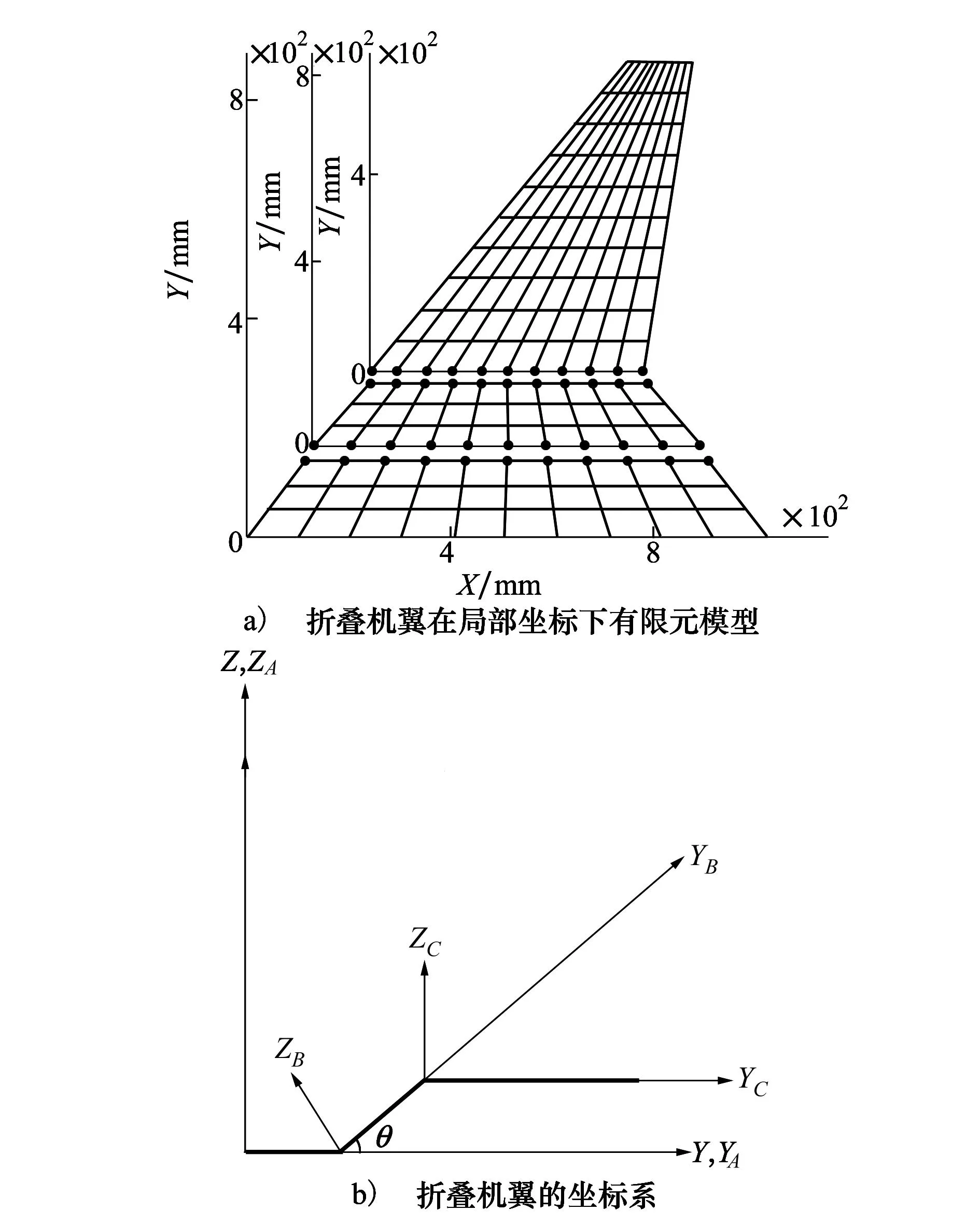
图1　折叠机翼的有限元模型和坐标系　(每个圆点代表铰链所处位置)

1.1参数化的结构模型

各个子结构在局部坐标系下的无阻尼的动力学方程如下所示:

(1)

当采用图1中的坐标系时,子结构A与子结构C在总体坐标下与局部坐标系的位移矢量相同,不需要进行变换。对于子结构B,其在总体坐标系下的位移矢量与在局部坐标系下的位移矢量有如下关系:

(2)

式中,T为位移转换矩阵。同时对子结构B的动力学方程的两边左乘以T,就完成了子结构B的动力学方程从局部坐标系向总体坐标系的过渡。

为了方便模态综合法的应用,将各个子结构在总体坐标系下的位移分为内部节点位移和界面节点位移,对质量矩阵和刚度矩阵进行分块。以子结构A为例,其动力学方程为:

(3)

式中,i代表内部节点位移,m代表MPC耦合的节点位移,s代表扭转弹簧耦合的节点位移。

对于子结构A进行模态分析,引入模态坐标pA以及模态矩阵φA,则:

(4)

类似地,引入模态坐标pB、pC以及模态矩阵φB、φC,对于子结构B和子结构C进行模态分析。此时,整体动力学方程可以写成如下形式:

(5)

1.2参数化的气动力模型

本文采用偶极子网格法获得了折叠机翼的气动力模型。考虑到各个子结构的升力面之间的相互干扰,每个升力面上的压力分布Δp与气动网格控制点的无量纲法洗幅值w满足如下关系:

(6)

式中,D为非定常气动力影响系数矩阵,ρ为密度,V为速度。

在简谐振荡的假设下,根据非定常气动力的边界条件,w与气动网格节点的法向位移z有如下关系:

(7)

式中,k为减缩频率,b为参考长度。由于气动网格与结构网格是独立的,因此在进行气动弹性分析时,需要进行力和位移的转换,此时可以采用样条插值法来实现,如无限板样条,薄板样条等。其位移转换关系为:

(8)

式中,φ=blockdiag(φA,φB,φC),Gs1和Gs2为位移插值转换矩阵。根据虚功原理,可以得到作用在结构网格节点的等效力:

(9)

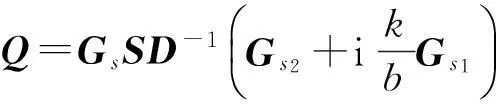
1.3气动弹性系统的状态方程

在整体动力学方程中引入作用在结构网格节点的等效力:

(10)

式中,模态坐标p中各个分量并不独立,对各个子结构进行综合,消去非独立的模态坐标便可以得到整体的气动弹性模型。引入独立模态坐标变换矩阵Π,并左乘ΠT,则独立模态坐标下的气动弹性方程为:

(11)

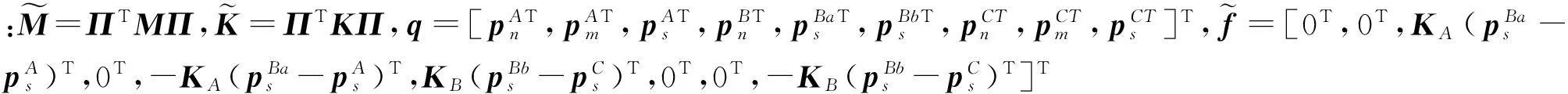
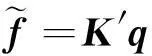
(12)

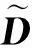
(13)

此时Q为离散形式的频域气动力。为了建立状态空间的气动弹性模型,利用有理函数近似,如Roger法,最小状态法等可以获得时域内的气动力。这里采用最小状态法进行频域气动力的有理近似,引入空气状态变量qa,则公式(13)表达为状态空间的形式为:

(14)

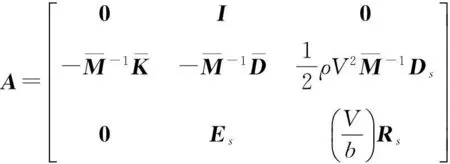
V2ΠTA0Π。

此时A与折叠角θ,扭转弹簧刚度KA、KB均有关。系统的稳定性由A的特征值来确定:当速度V小于颤振速度VF时,全部特征值均位于复平面的左半部;当速度V增加到一定值时,出现一个系统特征值的实部由负值变为正值时,系统会变为不稳定的。当实部为零时,此时的速度V即为颤振速度。尽管该方法可以预测系统的颤振速度,但是当以简化颤振边界预测为目的时,计算量较大。反之,采用Gram矩阵可以有效地避免特征值的计算,提高计算效率。

2基于Gram矩阵范数气动弹性系统的稳定性预测

在现代控制理论中,其反馈信息是由系统的状态变量组合而成。但并不是所有的状态变量都能测量到,于是提出了能否通过对输出的测量获得全部状态变量的信息,便成了系统的可观性问题。对于线性时不变的稳定系统,其可观Gram矩阵可由下面的Lyapunov矩阵获得[10]:

(15)

根据文献[10],输出的状态变量所具有的能量,可以通过可观Gram矩阵来体现。但是此时,Wo矩阵不能采用公式(15)来求解。这是因为公式(15)只适用于稳定系统。当颤振发生时,系统是不稳定的。所以文献[10]对其进行了修正,使得Wo的求解不受系统稳定性的影响。假设X是以下Riccati方程的解:

XF+FTX-XGGTX=0

(16)

(F+GMg)W+W(F+GMg)T+GGT=0

(17)

这里将Wo的矩阵范数σ作为参数,此时不同速度V和C对应一个σ,该值意味着机翼从来流中获得的能量在结构上的累积。当C相同时,随着速度的增加,σ会达到最大值,该阶模态不稳定;倘若随着速度的增加,σ没有最大值出现,则该阶模态是稳定的,进而可以确定不稳定模态以及颤振速度[10]。

3折叠机翼的颤振参数化分析

折叠机翼的各个子结构的质量矩阵和刚度矩阵通过DMAP语言获得。采用DLM(doubletlatticemethod)获得折叠机翼在频域下的气动力,通过最小状态近似,最终获得了折翼机翼的气动弹性方程在状态空间的表达形式。在公式(14)中,ρ=1.226kg/m3,M∞=0.0,采用前6阶模态参与计算,KA=KB=1Nm/rad。最后利用文中的Gram矩阵的F范数,确定了折叠机翼的颤振边界,整个程序的编制均在MATLAB中完成。

3.1基于Gram矩阵范数颤振边界预测的有效性验证

首先以机翼完全展开和完全折叠为例,即θ=0°和θ=120°,获得了其颤振边界。为了验证方法的有效性,将结果与采用特征值法的结果进行了对比,在验证的过程中均没有考虑结构阻尼。

3.1.1机翼完全展开(θ=0°)

当θ=0°时,各阶模态的范数σ随速度的变化如图2所示。

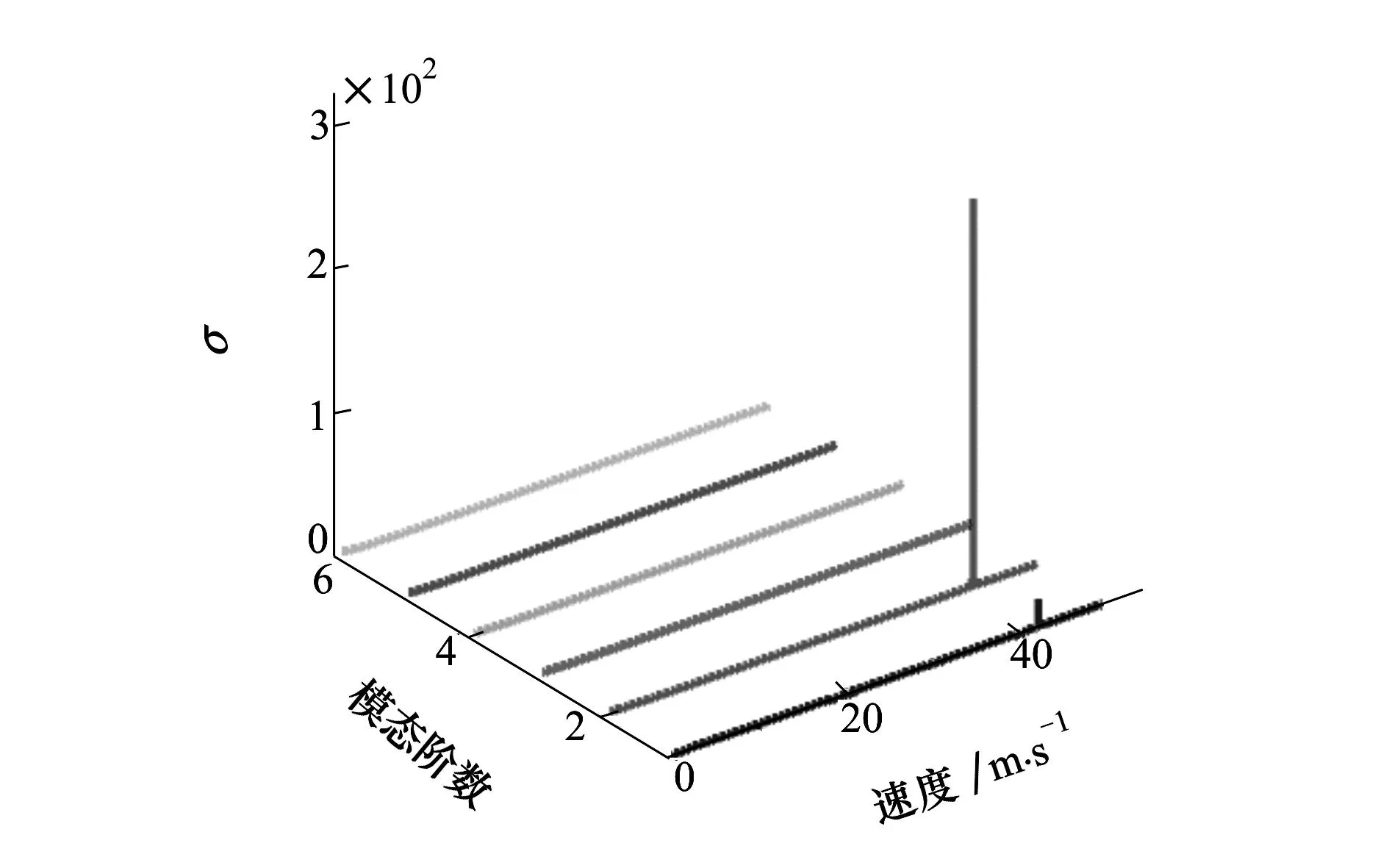
图2　范数σ随来流速度的变化(θ=0°)

从图2中可以发现,随着速度的增加,第1阶模态与第2阶模态的σ,在接近42.7 m/s时达到了最大值,并且第2阶模态σ的最大值明显高于第1阶,说明第2阶模态不稳定,其余各阶模态的σ均没有最大值出现。这一现象表明第1阶模态与第2阶模态相互耦合,使得结构耗散的能量小于从来流中吸收的能量,达到颤振临界点而发生颤振现象。与特征值法得到的结果对比如表1所示。

表1　颤振结果对比(θ=0°)

3.1.2机翼完全折叠(θ=120°)

当θ=120°时,各阶模态的范数σ随速度的变化如图3所示。

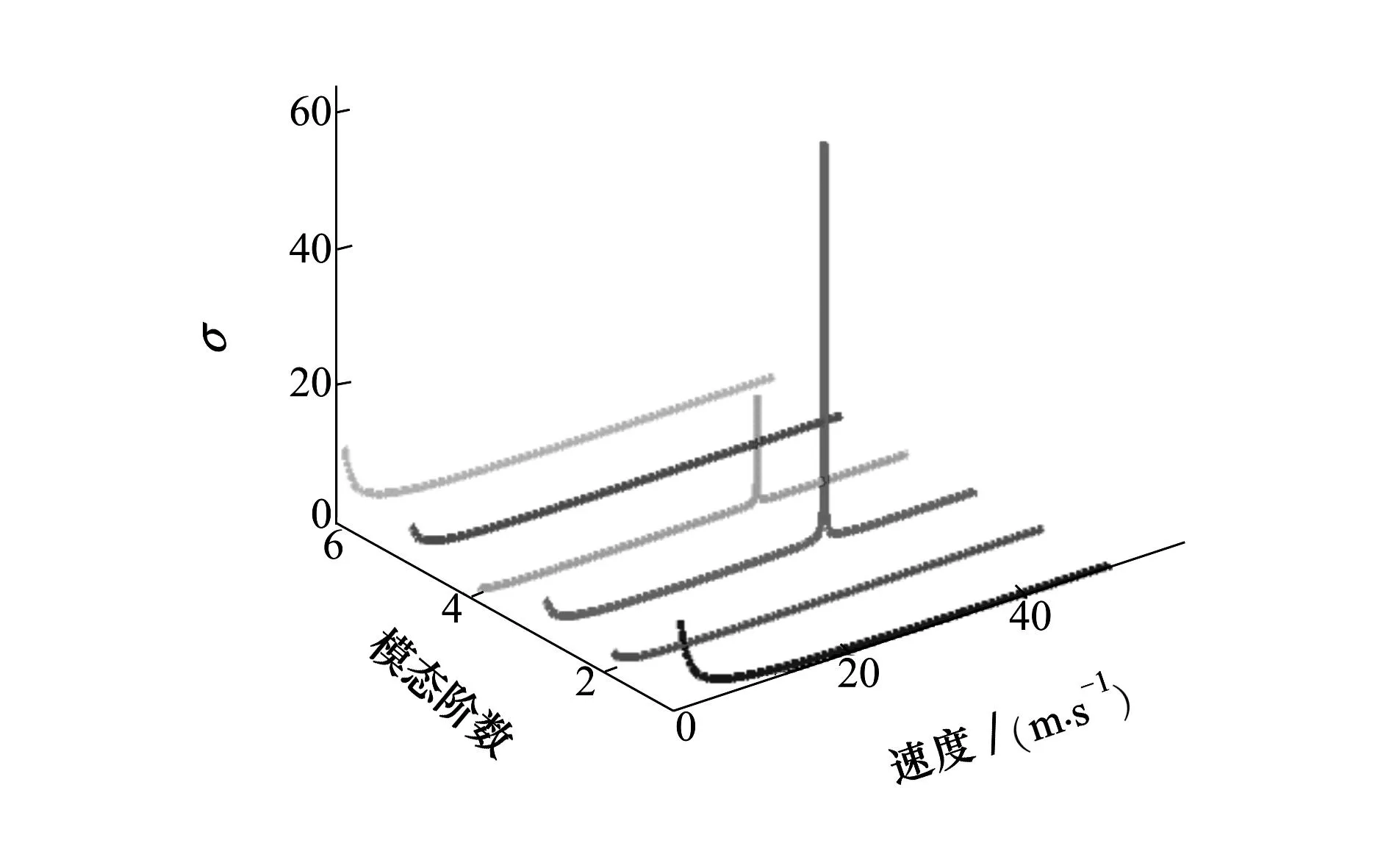
图3　范数σ随来流速度的变化(θ=120°)

从图3中可以看出,第3阶模态和第4阶模态的σ,在32.7 m/s附近,达到了最大值。随着速度的增加,其余各阶模态的σ没有最大值出现。第3阶模态的σ最大值明显高于第4阶,说明第3阶模态不稳定。与特征值法得到的结果对比如表2所示。

表2　颤振结果对比(θ=120°)

由于颤振发生时,总是伴随着模态之间的耦合,在某2个模态耦合较强的情况下,产生了能量转换而发生颤振,所以在这2个例子中,均有2阶模态的σ出现了最大值,意味着这2阶模态的耦合作用较强,使得结构从气流中吸收能量,达到颤振临界点而发生颤振。这些与颤振发生的机理保持一致。从表1和表2 的对比结果可以看出:本文方法与特征值法获得的颤振速度的相对误差较小,对于不稳定模态的预测也吻合。表明本文方法可以获得与特征值法精度相当的结果。

3.2颤振边界的分析

颤振速度随折叠角的变化情况如图4 所示。

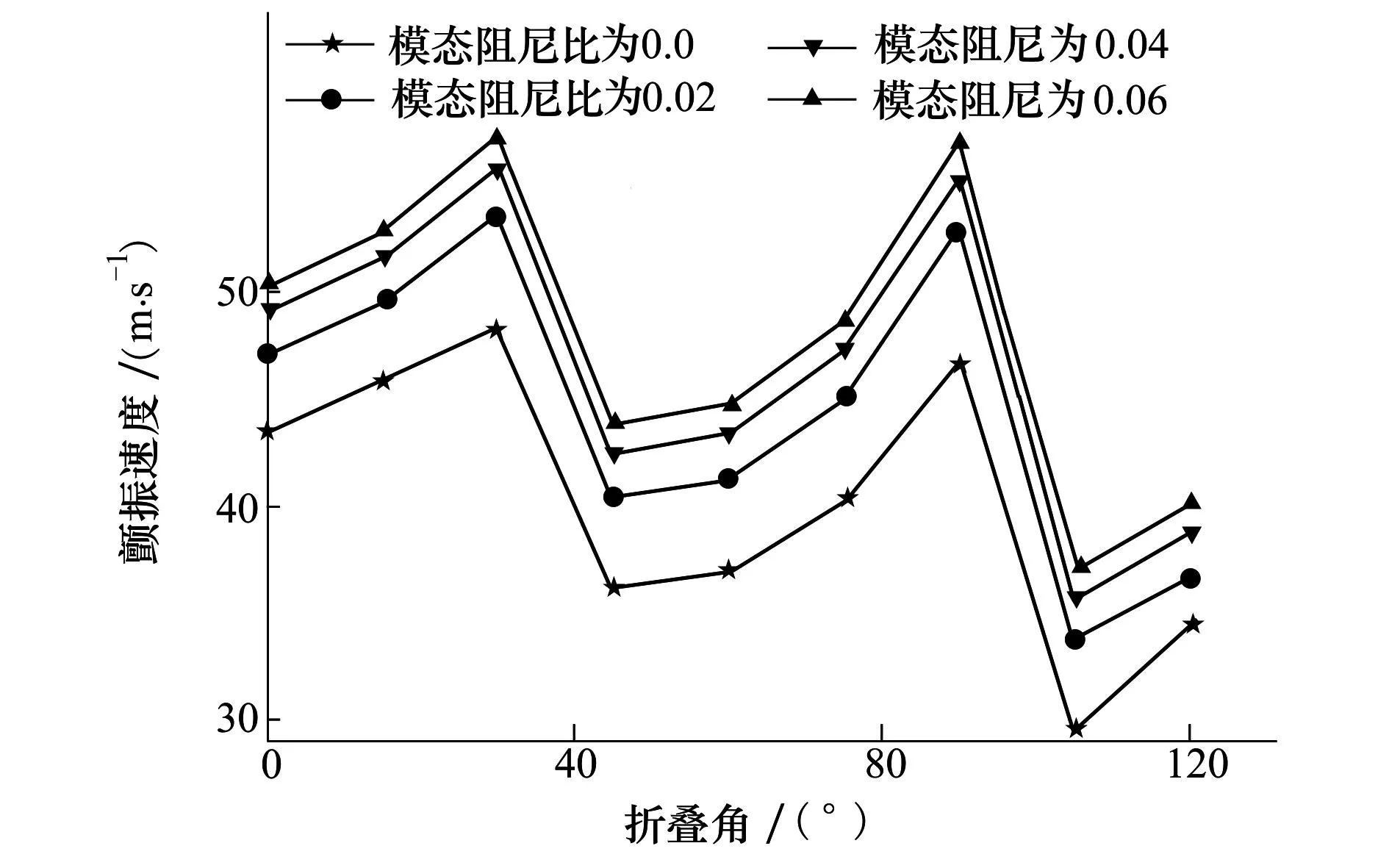
图4　颤振速度随折叠角的变化

随着折叠角的增加,颤振速度并不是折叠角的单一函数。在某些折叠角度范围内,如45°≤θ≤90°,颤振速度随着折叠角的增加而增加;在某些折叠角度范围内,如30°<θ<45°,颤振速度随着折叠角的增加而减小。折叠角在接近30°时,颤振速度达到了最大值,即48.36 m/s;折叠角在接近105°时,颤振速度达到了最小值,即29.59 m/s。即在整个折叠过程中,颤振速度的变化幅度很大。显然,折叠角对颤振速度有很大的影响。这主要是由于折叠角的变化,使得结构的质量矩阵,刚度矩阵以及气动模型均发生了很大的变化。从表3 中,可以看出,随着折叠角的增加,颤振不稳定的模态也发生了变化,从第2阶模态过渡到了第3阶模态。

表3　不稳定模态随折叠角的变化

值得注意的是,在不同的折叠角度下,随着模态阻尼比的增加,颤振速度均有所提高。这是由于较高的模态阻尼比能够抑制不稳定的模态之间的耦合,提高结构的能量耗散,减小从来流中吸收的能量在结构上的累积,推迟颤振现象的发生。

4结论

本文建立了折叠机翼颤振分析的参数化气动弹性模型,该模型以折叠角和内外铰链刚度为参数,可以有效地形成不同构型下的折叠机翼的气动弹性模型。根据控制理论中的Gram矩阵范数获得了折叠机翼的颤振边界,可以得出以下结论:

1) 提出一种适合折叠机翼的参数化的气动弹性模型。该模型具有以下优点:适用于类似折叠机翼的多段机翼结构;结构模型和气动力模型均不需要重复建立。

2) 采用Gram矩阵范数预测气动弹性系统的稳定性,可以定性地分析参与颤振耦合的模态信息,避免高维气动弹性系统的特征值求解,提高计算效率。

3) Gram矩阵的范数,不仅仅局限于F范数,如1范数,无穷范数等。当采用不同范数时,得到的颤振速度基本不变。

4) 由于折叠角对机翼结构以及气动特性有很明显的影响,使得颤振速度对折叠角很敏感;并且随着折叠角的增加,出现了不稳定模态之间的过渡。

5) 在一定的范围内,结构的模态阻尼比可以提高折叠机翼的颤振速度。

参考文献：

[1]Wilson J R. Morphing UAVs Change the Shape of Warfare[J]. Aerospace America, 2004, 42(2): 28-29

[2]Tang D, Dowell E H. Theoretical and Experimental Aeroelastic Study for Folding Wing Strucutres[J]. Journal of Aircraft, 2008, 45(4):1136-1147

[3]Snyder M P, Sanders B, Eastep F E, Frank G J. Vibration and Flutter Characteristics of a Folding Wing [J]. Journal of Aircraft, 2009, 46(3): 791-799

[4]Wamg I, Gibbs S C, Dowell E H. Aeroelastic Model of Mutisegmented Folding Wing: Theory and Experiment[J]. Journal of Aircraft, 2012, 49(3): 911-921

[5]Zhao Youhui, Hu Haiyan. Paremeterized Aeroelastic Modeling and Flutter Analysis for a Folding Wing[J]. Journal of Sound and Vibration, 2012,331(2): 308-324

[6]杨智春, 谷迎松, 夏巍. 基于矩阵奇异值理论的颤振分析新方法[J]. 航空学报, 2009, 30(6): 985-989

Yang Zhichun, Gu Yingsong, Xia Wei. New Type of Flutter Solution Based on Matrix Singularity[J]. Acta Aeronautica et Astronautica Sinica, 2009,30(6): 985-989 (in Chinese)

[7]Moore B C. Principal Component Analysis in Linear Systems: Controllability, Observability, and Model Reduciton[J]. IEEE Trans on Automatic Control, 1981, 26(1): 17-32

[8]Hyounsurk Roh,Yongjin Park. Actuator and Exciter Placement for Flexible Structures[J]. Journal of Guidance, Control and Dynamics, 1997, 20(5): 850-856

[9]Rowley C W. Model Reduction for Fluids, Using Balanced Proper Orthogonal Decomposition[J]. International Journal of Bifurcation and Chaos, 2005, 15(3): 997-1013

[10] Bueno D D, Marqui C R, Goes L C S, Goncalves P J P. The Use of Gramian Matrices for Aeroelastic Stability Analysis[C]//Mathematical Problems in Engineering, 2013

Parametric Aeroelastic Modeling and Flutter Analysis for a Folding Wing

Ni Yingge, Hou Chi, Wan Xiaopeng, Zhao Meiying

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:As for the characteristics of a folding wing, a parametric aeroelastic model for flutter analysis is proposed in this paper. Parametric structural model is achieved based on modal synthesis method. Parametric aerodynamic model is established using doublet lattice method. And the flutter boundary prediction of an aeroelastic system is elaborated using Gram matrix norm. The fully extended and completely folded configurations are taken as examples. The results of this method are compared with those of eigenvalue method to verify the correctness. Some analyses of different folding angles are performed. Flutter boundary is very sensitive to the folding angle. With increasing folding angle, the flutter mode changes. Higher modal damping ratio can raise flutter speed and delay flutter phenomenon.

Key words:Folding wing, Gram matrix, parametric model, aeroelasticity; flutter, eigenvalues and eigenfunctions, finite element method, MATLAB, Riccati equation, stability

中图分类号：V271.4

文献标志码：A

文章编号:1000-2758(2015)05-0788-06

作者简介：倪迎鸽(1987—),女,西北工业大学博士研究生,主要从事变体飞机的一体化设计的研究。

收稿日期：2015-04-09