采用窗函数法进行数字信号截短的优化算法*

周冬跃 ，林海全 ，张洪林 ，李学识 ，黄继才

（1.广东工业大学 物理与光电工程学院，广东 广州 510006；2.广州致远电子股份有限公司，广东 广州 510660；3.华南理工大学 电子与信息学院，广东 广州 510641；4.广东工业大学 自动化学院，广东 广州 510006）

0 引言

对一个时域信号进行有限时间片段的分析时，如果对数字信号进行直接截短，就会导致频谱泄露，从而导致信号分析出现差错，影响信号分析的精度，以至难以满足应用要求[1-3]。对此，国内外学者提出了一系列改进数字信号截短的方法。文献[4-5]研究了频谱泄露的原因以及加窗函数后频谱泄露的特性。文献[6]对海明窗(Hamming Window)、汉宁窗(Hanning Window)在信号截短中的时谱特性进行比较分析。文献[7]分析矩形窗(Rectangular Window)、海明窗、汉宁窗和布莱克曼窗(Blackman Window)对截短时域和空域信号产生的影响。然而，这些研究都局限在理论和仿真分析，其对应的方案尚未结合FPGA硬件应用需要。

为了解决工业产品设计中的频谱泄露问题，文中基于FPGA硬件系统，对集成矩形窗、海明窗、汉宁窗和布莱克曼窗四个窗函数的系统进行优化设计，在频谱泄露特性、速度和硬件资源等方面对现有的设计方案进行了较大的优化，从而提高了系统的综合性能。

1 窗函数的设计

该方法的基本思路是：首先利用坐标旋转数字计算(CORDIC)迭代方法产生余弦函数，然后利用式(1)～式(4)分别所表示矩形窗、海明窗、汉宁窗和布莱克曼窗函数实现基于FPGA的矩形窗、海明窗、汉宁窗和布莱克曼窗的信号截短方案。

由式(1)～式(4)可见，为了实现这些窗函数，首先要解决余弦函数中相位的求解，其次计算余弦函数，最后完成加减运算。其中，CORDIC迭代算法提供一种逼近的方法求得余弦值。

限 制 该 算 法 中 的 旋 转 相 位 θi，使 得 tanθi=2-i， 即 θi=tan-12-i。CORDIC迭代可用如式（5）所示的方程组表示：

其中，di=+1，zi≥0；di=-1，zi＜0，用于确定旋转方向。 依据迭代公式，设计硬件结构，框图如图1所示。

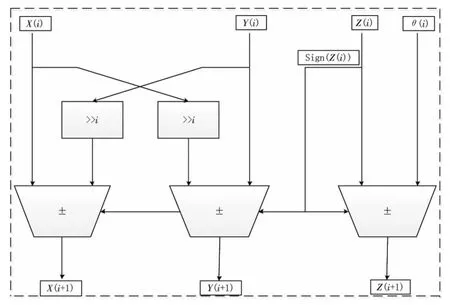
图1 CORDIC迭代电路结构

在圆周旋转模式中，i取值越大输出精度越高，令i=n时能满足设计要求，那么经过n次迭代后：

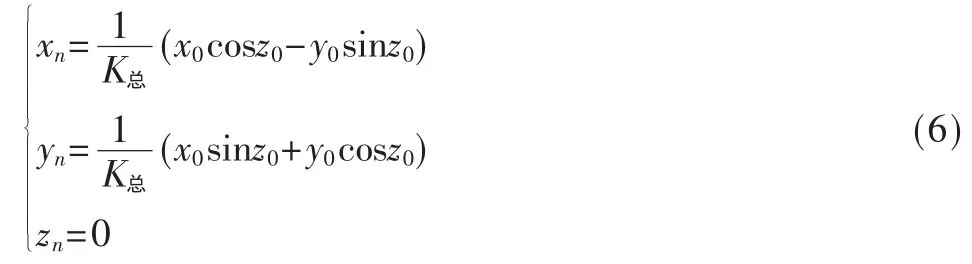
通过设置x0=K总和y0=0就可以计算xn=cosz0和yn=sinz0了，其中，z0为输入相位，K总=cosθ0×cosθ1×…×cosθn。

2 窗函数的优化

2.1 CORDIC迭代参数优化

CORDIC是系统的核心模块，由式(6)可知这是一个迭代的过程，为了使CORDIC算法模块能够辨认并计算本设计的最小刻度相位，同时考虑节省迭代对应的资源开销，最后一次迭代所对应的旋转相位只要满足小于该最小刻度相位即可。约定文中设计的系统采样点数是256点至16 M点之间任意可选，当信号长度N为16 M点时，可获得本设计的最小刻度相位0.000 021 458°。经过式(6)的计算可得，在i=22时，即第 22次迭代所对应的旋转相位0.000 013 660°小于最小刻度相位，故将文中方案迭代次数确定为23。

2.2 窗函数的结构优化

进一步分析式(1)～式(4)四个窗函数的表达式，发现这些表达式具有相同的结构，因此可以将它们合并为一条通用的表达式，如式（7）所示：

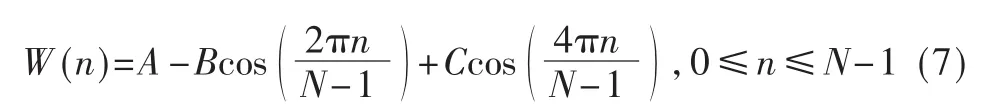
不同窗函数对应不同的窗系数A、B、C，各窗函数对应的具体系数由式(1)～式(4)可以得出，在设计时，这些窗系数可由一个两位二进制变量的值来确定。

由于在任一时刻只有一个窗函数在工作。此特点满足了资源共享的条件，因此可以对方案所需的资源进行共享优化，4种窗函数使用相同的CORDIC和乘法器，图2(a)和图2(b)分别为优化前和优化后的电路结构。

从图中可以看出，优化后的结构可以大大减少FPGA内部的硬件消耗。

表1为设计优化前后在FPGA器件中布局布线所消耗的资源情况，可见优化后设计所消耗的各类资源比优化前减少了20%～51%。

2.3 速度的优化设计

整个设计采取了恰当的流水线技术对速度进行优化，其基本思路是：在组合逻辑较长的路径上插入几级寄存器，从而大大提高了数据的吞吐量。经过增加流水线级数的方法，时钟周期比流水线设计前小，从而提高运行速度。图3为迭代过程流水线设计之前和之后的模块图。

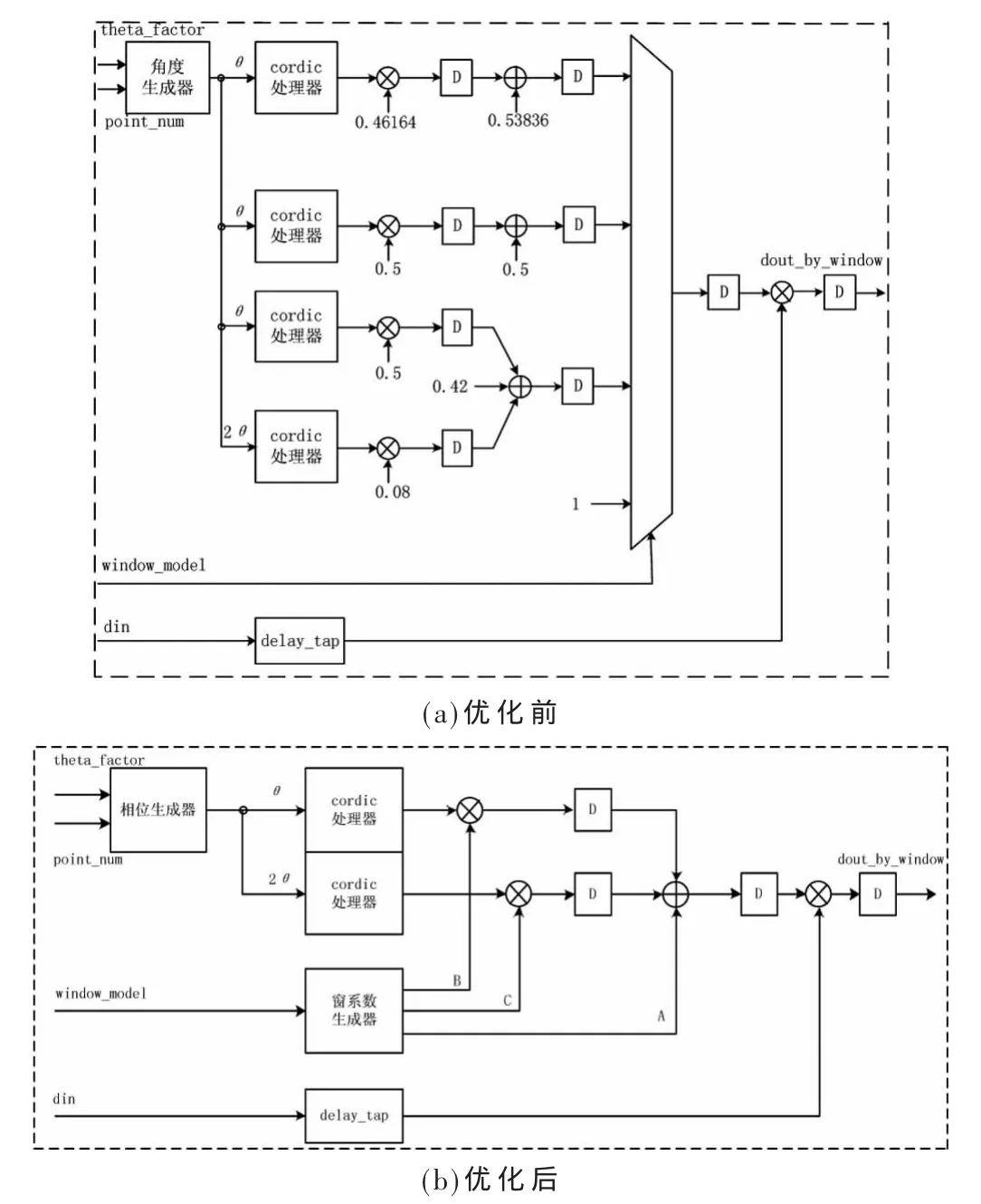
图2 优化前后的电路结构对比

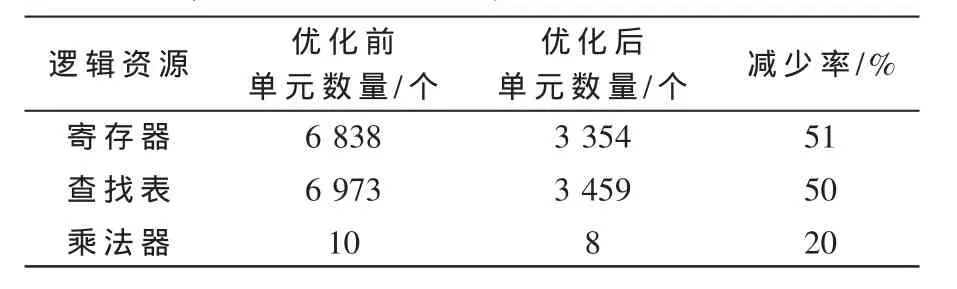
表1 优化前后资源消耗对比

图3 CORDIC迭代过程流水线时序优化

对于图3(a)所示的优化前的方案，仅能通过30 MHz的时序约束。假设系统运行于30 MHz的频率下，数据从进入系统到输出结果需要19个时钟周期，即633 ns。而对于图3(b)所示优化后方案，进行流水线设计之后可以通过360 MHz的时序约束，数据从进入系统到输出结果需要42个时钟周期，即117 ns。很明显，经过流水线设计后，系统的运行速度大大提高。此外，流水线设计使系统每个时钟处理一个数据，不用等到一个数据完全输出才进行下一个数据的处理。

3 窗函数对抑制频谱泄漏方案的实现和分析

3.1 系统整体实现

文中窗函数采用点数可调，令信号是长度256点到16 M点动态可调的窗函数控制器，即需要根据不同的信号长度为系统提供相应的相位因子。图4所示为窗函数计算过程的流程图，相位生成器根据FPGA中的主控器MicroBlase传来的相位因子和信号长度两个参数产生相应时刻的相位，然后CORDIC模块根据该相位计算相应的余弦值，接着根据当前窗函数类型选择相应的窗系数并完成窗函数计算，最后利用窗函数结果对输入信号进行加窗处理。

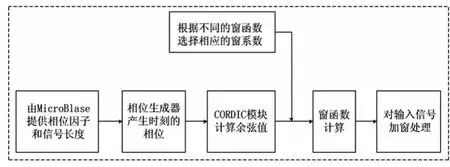
图4 窗函数计算流程图

3.2 整体仿真效果和分析

为了分析文中方案对频谱泄露的特性，对文中的窗函数法采样数据的频谱特性进行实验和分析。首先对实验信号 y(t)=40×[sin(40πt)+sin(120πt)]进行采样，采样频率为1 000 Hz，采用点数共1 571点，modelsim仿真软件通过读取该文件数据对文中所设计的系统进行仿真并将仿真结果保存在文本文件中，采用仿真进行频谱分析，结果如图5所示。

分析矩形窗、海明窗、汉宁窗和布莱克曼窗的4种情况中旁瓣衰减，它们的第一旁瓣相对于主瓣衰减和主瓣宽度如表2所示。

由频谱图可以看出，对信号加矩形窗(图5(a))处理，有明显的频谱泄露；而对信号加海明窗(图 5(b))、汉宁窗(图 5(c))或布莱克曼窗(图 5(d))处理后，则频谱泄露明显减小。海明窗、汉宁窗和布莱克曼窗主瓣加宽，旁瓣则显著减小。从减小泄漏观点出发，汉宁窗优于矩形窗，布莱克曼窗最好，但主瓣加宽，相当于频率分辨力有所下降。相对而言海明窗加权的系数能使主瓣宽度更小。布莱克曼窗主瓣较宽，旁瓣衰减达到-59.3，频谱泄露最小，幅值识别精度最高，但频率识别精度最低。可见，基于FPGA的窗函数截短，相对于直接截短的方式，采用文中窗函数处理方案，信号的频谱泄露特性得到较好改善。

4 结论

文中所提出的方案对矩形窗、海明窗、汉宁窗和布莱克曼窗进行了算法设计和方案优化。为了优化方案中的资源消耗和提高精度，采用了资源共享技术、选择合理的数据位宽以及为CORDIC模块选择合适的迭代次数；为了优化设计的速度，采用了流水线技术，从而较大提高处理的速度。最后，利用工具软件modelsim对系统进行了仿真，验证了算法对应的系统功能的正确性以及分析了系统的优化性能。

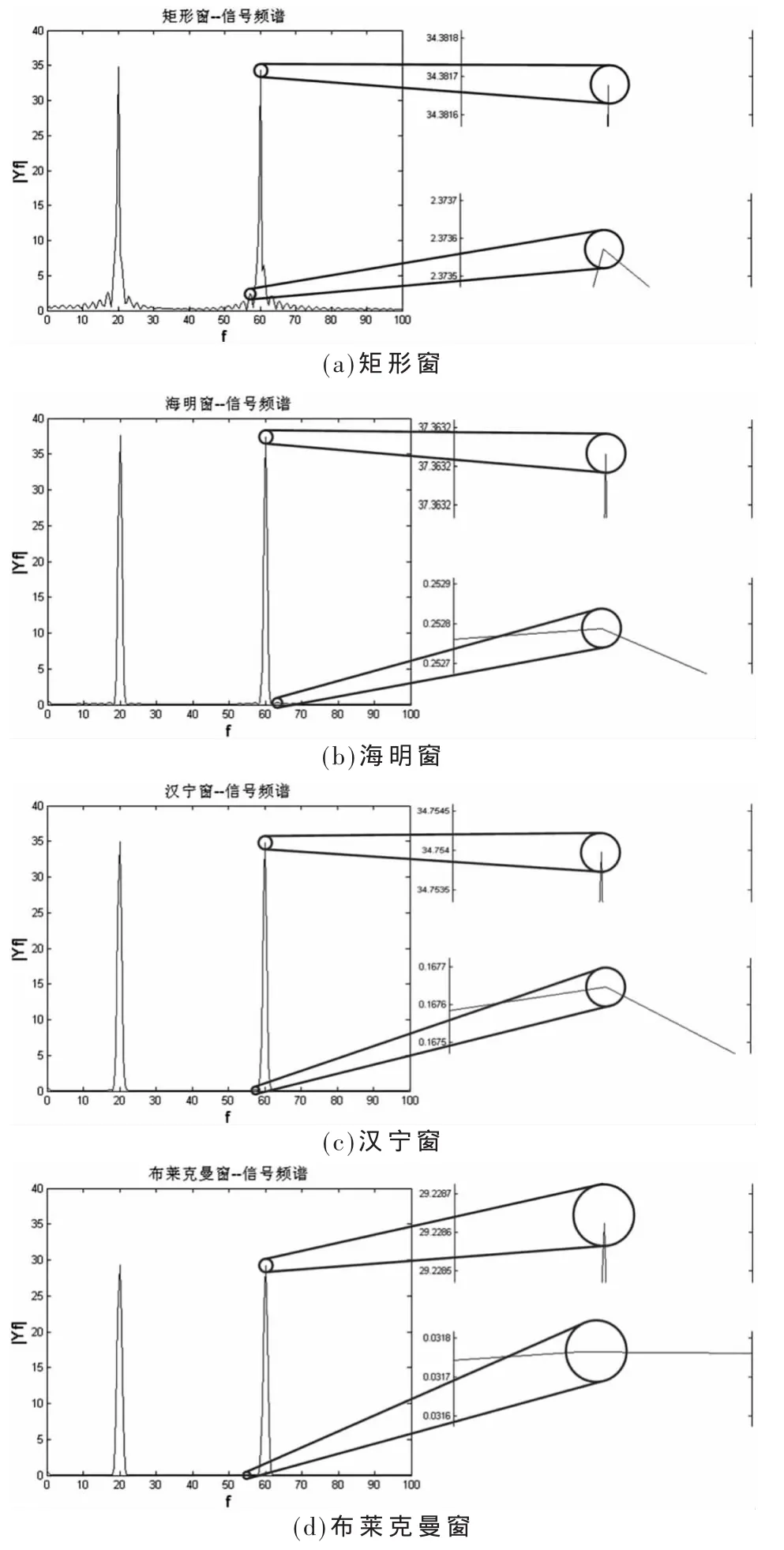
图5 加窗后的信号频谱特性

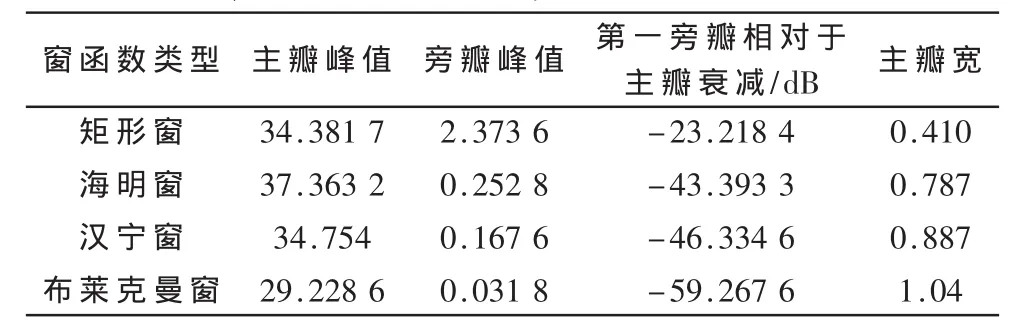
表2 优化前后资源消耗对比

[1]张斌，孔敏，吴从兵．基于窗函数下频谱泄露的研究[J]．信息化纵横，2009(11)：10-12．

[2]田园，周勖．窗函数在数字滤波器设计中的应用[J]．国外电子测量技术，2013，32(4)：25-27．

[3]郭建涛，刘友安，玉林．基于窗函数设计的跳频信号时域分析[J]．计算机应用，2011，31(9)：2333-2335．

[4]XUE H，YANG R．Optimal interpolating windowed discrete Fourier transform algorithms for harmonic analysis in power systems[J]．IEE Proceedings of Generation，Transmission and Distribution，2003，150(5)：583-587．

[5]RELJIN I S，RELJIN B D．Extremely flat-top windows for harmonic analysis[J].IEEE Trans.on Instrumentation and Measurement.2007，56(3)：1025-1041．

[6]DAVID C.Swanson.Precision spectral peak frequency measurement using a window leakage ratio function.Mechanical Systems and Signal Processing Volumes 54-55，March 2015：1-15.

[7]RAPUANO S，HARRIS F J.An introduction to FFT and time domain windows[J].IEEE instrumentation&Measurcmcnt Magazine，2007，10(6)：32-44.