对Shor算法破解RSA的探讨
2015-02-21凃玲英胡一凡张洪涛代永涛熊红梅
凃玲英, 胡一凡, 张洪涛, 代永涛, 熊红梅
(1. 湖北工业大学 纳米电子技术与微系统实验室, 湖北 武汉 430068;2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068)
对Shor算法破解RSA的探讨
凃玲英1,2, 胡一凡1,2, 张洪涛1,2, 代永涛1,2, 熊红梅1,2
(1. 湖北工业大学 纳米电子技术与微系统实验室, 湖北 武汉 430068;2. 湖北工业大学 电气与电子工程学院, 湖北 武汉 430068)
针对Shor算法具有随机性,会导致破解RSA公钥密码体制成功率不高的问题,对Shor算法原理、RSA公钥密码体制特点和大量计算结果进行分析,提出量子函数式f(x)=axmodn对a值的随机选取是有规律的.结合数论知识和蒙特卡洛法证明,结果表明:随机数a取完全平方数,所求周期r很可能不满足Shor算法要求;a取非完全平方数可以提高Shor算法破解RSA的成功率.
Shor算法; 非完全平方数; RSA算法; 公钥密码体制; 蒙特卡洛法.
迄今为止,RSA算法被认为是世界上最成熟完善的公钥密码体制.它能够抵抗已知的绝大多数密码攻击,已被ISO推荐为公钥数据加密标准.目前,世界上还没有任何可靠的方法破解RSA.随着Shor算法的提出和量子计算机的不断发展,RSA的安全性也受到威胁.Shor算法利用量子计算的并行性,可以快速分解出大数的质因子,它的提出在理论上破解了目前被公认为最安全的RSA公钥密码.Shor算法的基本原理是运用量子傅里叶变换,将大整数因子分解转化为求某一个函数的周期[1].但是在求函数周期过程中,现有的Shor算法随机性大,效率不高[2].鉴于此,本文通过对Shor算法和RSA算法原理的分析,并结合前人的研究成果,提出了一种可以提高Shor算法破解RSA成功率的方法.
1 RSA公钥密码
RSA使用公开的公钥进行加密通信,密文只能被拥有与之匹配的私钥的人解开.RSA算法的理论基础[3]是可逆模指数运算,它的安全性基于数论中大整数分解的复杂性.数论中,大整数分解的问题可概述为:已知整数n=p·q,其中,p和q是2个素数,求出p和q的值.
在RSA公钥密码体制中,用户拥有2个密钥:公钥PK={e,n}和私钥SK={d,n}.公钥用于加密,私钥用于解密.用户可将公钥PK公开,而私钥中的d必须严格保密.RSA公钥密码中相关参数的计算如下.1) 选取2个保密的素数p和q(p和q为100位以上的十进制数).2) 计算n=p·q的值.其中,n是RSA算法的模数.3) 计算φ(n)=(p-1)(q-1)的值,φ(n)是n的欧拉函数值.4) 随机选取1个整数e,使其满足1 设m为需要加密的明文,c为加密后的密文.加密时,先将明文比特串进行分组,让每个明文分组的十进制数mi小于n,记ci为对应的mi加密后的密文,则加密算法为 式(1)中:0≤mi 解密时,先对密文c进行比特串分组,则解密算法为 因此,RSA公钥密码体制中,最关键的是公钥PK中的e值和私钥SK中的d值. 2.1 原理描述 故 3) 求A和B,表达式为 得出 式(7)中:为保证A,B为整数,周期r应为非零偶数[5-6]. 2.2 周期r的求取 由A和B的表达式可知:只要求出函数f(x)的周期r,大整数n的因子分解问题就得到了解决.Shor算法中,周期r的信息是通过量子傅里叶变换获得的[7-8]. 首先,对2个量子寄存器R1和R2进行初始化,再对R1依次作H变换和幺正变换,得到的结果分别存放到R1和R2中.R1和R2中的状态为纠缠态,即 然后,对|R2〉进行测量.假设f(x)的周期为r.当|R2〉坍缩时,|R1〉也对应地坍缩为 式(11)中:A为小于(q-1)/r的最大整数. 最后,对|R1〉作量子傅里叶变换,并对其进行测量,求出函数f(x)的周期r,表达式为 量子傅里叶变换会使需要的结果增强,并使不需要的结果为0,这种现象称为量子干涉[9].所以,当c=kq/r,则 |R1〉经量子傅里叶变换后,周期从r变为q/r.由于c=kq/r,c和q是已知的,如果k与r互质,就能求出r[10].最大的非零偶数r,就是需要求的f(x)的周期. RSA的安全性取决于大整数n的分解,Shor算法的功能是分解大整数n,所以Shor算法在理论上破解了RSA公钥密码[11-12].破解过程具体如下6个步骤. 步骤1 通过量子傅里叶变换,求出函数f(x)的周期r,并保证r为非零偶数. 步骤2 将r带入式子(7),(8)中,结合待分解的大整数n,求出A和B的值. 步骤3 RSA中已销毁的p,q值分别是A,B. 步骤4 将p,q带入式子φ(n)=(p-1)(q-1)中,求出φ(n). 步骤5 将φ(n)和已知的e值带入式子d×e≡1 modφ(n)中,求出d值. 步骤6 将d,n的值带入式(2)中,完成了对RSA的破解. 4.1 优化思路 Shor算法虽然在理论上破解了RSA,但还是存在一些微小的不足的地方.应用Shor算法破解RSA,并不是大数n满足了条件就一定能成功破解,只是能使破解的成功率尽量接近1. 例1 函数f(x)=axmod 33,选取a=4,求周期r. f(0)=1,f(1)=4,f(2)=16,f(3)=31,f(4)=25, f(5)=1,f(6)=4,f(7)=16,f(8)=31,f(9)=25, … 此时周期r=5,不是偶数. 为了方便计算a取完全平方数时周期r的值,用C语言编写了一段程序,程序的源代码为 #include 〈stdio.h〉 #include 〈math.h〉 int gcd(int x,int y); void main() {int a,c,x,n; printf(″Please enter two int numbers:a=?,n=?
″); scanf(″%d,%d″,&a,&n); if(gcd(a,n)!=1 ‖ a>n) printf(″Please enter two correct int numbers b,n
″); else { x=1; c=1%n; while((int)(pow((double)a,(double)x))%n!=c) x++; printf(″函数f(x)的周期r是:%d
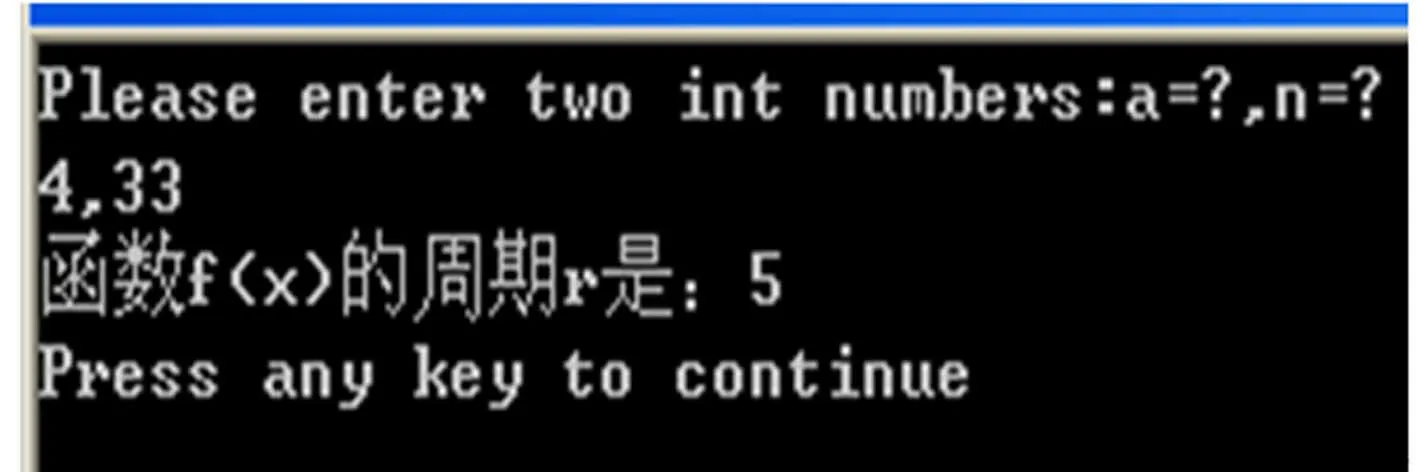
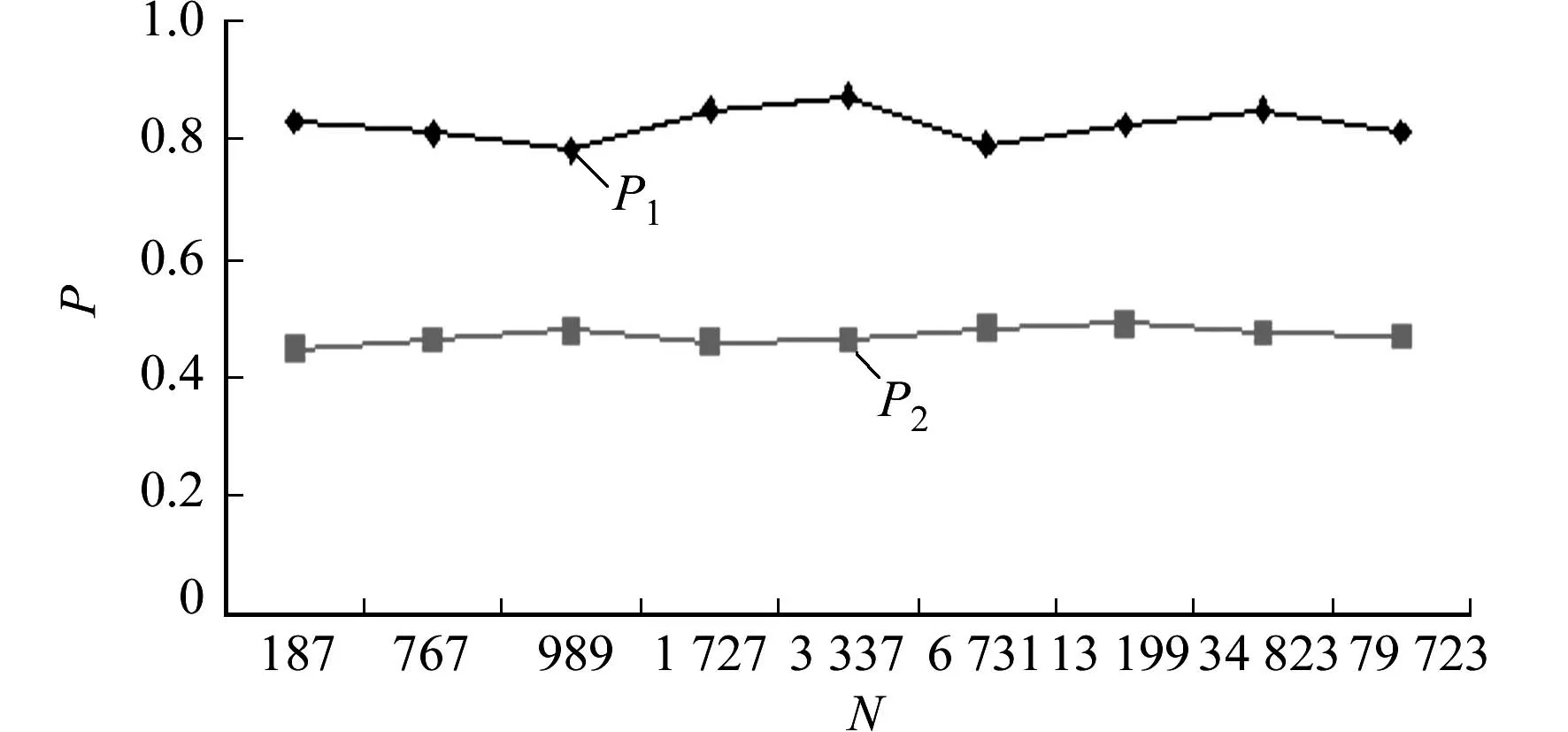
″,x); } } int gcd(int x,int y) { int z; if(x { z=x; x=y; y=z;} if(x%y = = 0) return y; else return gcd(y, x%y); } 图1 例1的验算结果 在Visual C++中运行程序验证例1的结果,验算结果如图1所示.由图1可知:当a=4时,周期r为5,例1的结果得到了验证.此程序方便求取r,为大量计算a取不同的完全平方数时对应的周期r提供了便利. 4.2 优化思路的证明 由例1可知:a取完全平方数算得的周期都不是偶数.通过计算发现,这是Shor算法周期求解中的大概率事件.如果对随机选取的a增加限制,不选取完全平方数,破解RSA的成功率会相应地提高[5]. 令p=2x+1,q=2y+1,且x≠y,则成功破解RSA的概率表示为 令d=gu,v为d的阶,这就等同于uv=0 mod(p-1),v最小. 当x≠y时,只需考虑x 所以,成功破解RSA的概率是 在x=y的情况下,此时概率为1,表示(a/n)=-1中的a总是满足条件1)和2). 从证明过程可看出,对a经过一定的限定,应用Shor算法破解RSA的成功率明显得到提高,说明优化思路是可行有效的.采用蒙特卡洛法作进一步分析. 列举不同的整数N值,算出a在2个条件下,函数f(x)的周期r为偶数的概率P,如表1所示.Shor算法能否高效破解RSA,对应函数式f(x)的周期r为偶数的概率P是重要指标.功能函数方程为 用蒙特卡洛法分析提高Shor算法破解RSA成功率的原理是:假设对大整数N进行M次随机抽样,求出每组P1,P2,并将其代入功能函数进行计算,得到M个T值.若T>0,则破解的成功率得到提升;若T≤0,则破解的成功率未得到提升. 图2 P1和P2的部分曲线分布 表1 a在不同条件下函数周期为偶数的概率 由图2可知:对于任意样本N值,P1均大于P2.对随机数a不做限定时,Shor算法成功破解RSA的概率P2不会超过50%;若限定随机数a取非完全平方数,破解的成功率P1不会低于75%,即T>0,说明Shor算法破解RSA的成功率得到提升. [1] HARDY G H,WRIGHT E M.An introduction to the theory of numbers[M].张晓尧,译.5版.北京:人民邮电出版社,2009:58-102. [2] 朱和贵.探析初等数论基本知识在密码学中的应用[J].山东工业技术,2014(21):253. [3] 李海峰,马海云,徐燕文.现代密码学原理及应用[M].北京:国防工业出版社,2013:110-114. [4] NAM Y S,BLUMEL R.Sealing laws for Shor′s alglorithm with a banded quantum fourier transform[J].Physica Review A,2013,87(3):032333. [5] 彭卫丰,孙力.SHOR量子算法的优化及应用研究[J].计算机应用与软件,2009,26(5):239-240,246. [6] NIELSEN M A,CHUANG I L.量子计算和量子信息(一)[M].赵千川,译.北京:清华大学出版社,2009:199-223. [7] 王蕴,黄德才,俞攸红.量子计算及量子算法研究进展[J].计算机系统应用,2011,20(6):228-231. [8] 徐炜,肖智,杨道理.量子算法在大数据挖掘中的应用前景浅析[C]∥中国信息经济学会学术年会暨博士生论坛论文集.广东:中国信息经济学会,2013:2-7. [9] 付向群,鲍皖苏,王帅.ZN上离散对数量子计算算法[J].计算机学报,2014,37(5):1058-1062. [10] GARCIA-MATA I,FRAHM K M,SPEPELYANSKY D L.Effects of imperfections for Shor′s factorization algorithm[J].Physical Review A,2007,75(5):2311. [11] LUCERO E,BARENDS R,CHEN Y,et al.Computing prime factors with a Josephson phase qubit quantum processor[J].Nature Physics,2012,8:719-723. [12] THOMPSON M G,POLITI A,MATTHEWS J C F,et al.Integrated waveguide circuits for optical quantum computing[J].Circuits, Device and System, IET,2010,5(2):94-102. (责任编辑: 黄晓楠 英文审校: 吴逢铁) Discussion on Cracking RSA With Shor Algorithm TU Lingying1,2, HU Yifan1,2, ZHANG Hongtao1,2, DAI Yongtao1,2, XIONG Hongmei1,2 (1. Nanoelectronics and Microsystems Technology Laboratory, Hubei University of Technology, Wuhan 430068, China; 2. School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China) Since the randomness of Shor algorithm could lead to low success rate in cracking RSA. By analyzing the principle of Shor algorithm, characteristics of RSA public key password system and lots of data, the view that the way for quantum functional in randomly selecting value is regular was putting forward .Verified by number theory and Monte Carlo method, the results showed that if takes a perfect square, the cycle probably can′t meet the requirements of Shor algorithm. It comes to a conclusion that take a non-perfect square can improve the success rate of Shor algorithm in cracking RSA. Sahor algorithm; non-perfect squares; RSA algorithm; public key password system; Monte Carlo method 1000-5013(2015)06-0640-05 10.11830/ISSN.1000-5013.2015.06.0640 2015-05-24 凃玲英(1963-),女,副教授,主要从事量子通信与量子计算、视频监控系统的研究.E-mail:947392311@qq.com. 湖北省武汉市科技局“十城千辆新动力汽车计划”项目(2013011801010600) TP 301.6 A2 Shor算法

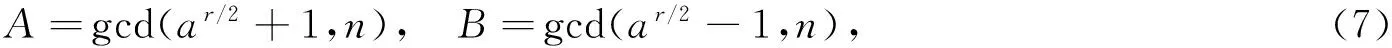
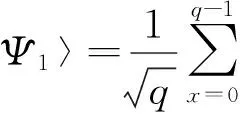
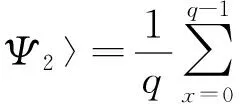

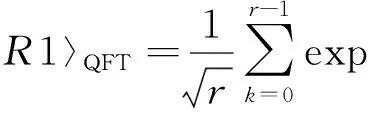
3 Shor算法在破解RSA中的应用
4 对Shor算法破解RSA的优化
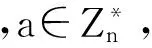
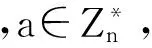
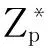



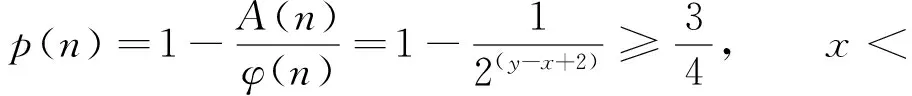



5 结束语

