整体涡轮转子空间寻位数控加工技术研究

■太重（天津）滨海重型机械有限公司 （300450） 杨实禹 张风祥 张 超

整体涡轮转子空间寻位数控加工技术研究

■太重（天津）滨海重型机械有限公司 （300450） 杨实禹 张风祥 张 超

摘要：整体涡轮转子是影响分子泵抽真空性能的关键零件。针对分子泵整体涡轮转子的结构特征如多层旋转叶片、对称性要求高以及装夹找正困难等，将空间寻位数控加工技术应用于其多层叶片铣削加工中。加工时首先确定转子毛坯各层叶片轴线所在空间位置，再经空间矩阵变换得到转子1至6层叶片的装夹偏差在X/Y/Z向的偏移分量，在此基础上利用编制的中间转换器一次性修正转子数控加工程序，实现分子泵整体涡轮转子多层叶片的精密铣削加工。

分子泵是利用高速旋转的转子把动能传输给气体分子，使之获得定向速度从而被压缩驱至排气口抽走的机械式真空泵。近30年半导体产业的飞速发展，使分子泵越来越受到重视，并得到快速发展。

由于分子泵涡轮转子是高速旋转（转速为70 000r/min）的回转体零件，加工装夹误差要求保证在20μm以下。使用传统“定位-加工”运行模式的数控加工方法加工分子泵涡轮转子时，装夹找正过程依赖操作工人经验，生产批次不稳定，严重影响整体加工周期，阻碍生产效率的提高。因此探索应用新型的自寻位数控加工模式加工此部件。

空间寻位方法是通过测量的手段，得到工件毛坯相对于理想加工位置的偏移量，根据此偏移量修正数控程序，实现精确加工的目的。此方法与传统加工模式的不同之处在于不是努力地“摆正”工件后再对其进行加工，而是对装夹后的工件进行位置测量，得到装夹后没有“摆正”的工件相对于理想位置的偏移量及偏斜角，在承认其位移及角度偏差的基础上直接对数控代码进行修正，最后保证加工出符合图样要求的工件。由于转子毛坯的实际位置与理想位置存在偏移量与偏角，修正数控程序时要根据转子毛坯的空间装夹位置实施坐标变换。本文提出使用直线位移传感器测量转子外圆确定其轴线空间位置的方法，并基于变换矩阵得到了转子中心轴线偏差在三维空间内的分量，最后给出了应用实例。

图1　涡轮转子毛坯、装夹工位及零件

1. 涡轮转子各叶片层圆心空间位置检测原理

分子泵涡轮转子毛坯、装夹方式及最终零件如图1所示。由于分子泵涡轮转子是具有多层叶片的回转类零件，所以出现的相对于理想位置的偏角与偏移量都属于空间位置变化，使用传统测量工具无法对其空间位置进行准确测量，且要求操作工人有较强的工作经验。

现阶段使用传统“定位-加工”模式加工涡轮转子，在装夹定位转子毛坯时，使用机械式百分表测量转子外圆，观察百分表位移变化再进行手工调整。受此启发，我们提出一种由外圆轮廓确定平面圆心，再由平面圆心确定转子空间位置的方法。

由于涡轮转子有6层叶片，设从第1层到第6层的圆心分别为A0、B0、C0、D0、E0和F0，各圆心均处于转子轴线上。在转子毛坯的第1层和第6层处安装拉杆式位移传感器测量转子外圆，此过程与机械式百分表测量过程相同。如图2所示，A、F为转子毛坯上的两个测量位置，A处于第1层加工面，F处于第6层加工面。

传感器测量头与转子外圆直接接触，控制分度盘缓慢匀速旋转一周，当转子实际位置与理想位置存在偏差时，测量头产生位移，传感器输出位移信号，将提取到的位移信息存储在寄存器中，经过信号处理拟合成位移曲线（见图3）。位移曲线波谷α0位置处为转子毛坯最大偏心位置，所对应M轴上l0位置的值为最大偏心距离。

2. 转子圆心空间位置坐标变换

涡轮转子叶片加工采用铣削加工方式，转子毛坯装夹在机床分度盘上，刀具垂直于转子轴线，铣削路径为平行四边形。加工完一片叶片后机床分度盘旋转至下一加工位置，刀具重复上一路径进行铣削加工。

（1）确定转子轴线空间位置坐标：由于涡轮转子安装时产生偏心，所以转子的实际装夹位置与理想位置不重合，为方便观察，将第1加工层圆心A0与第6加工层圆心F0投影到机床坐标系XOZ平面上 （见图4）。

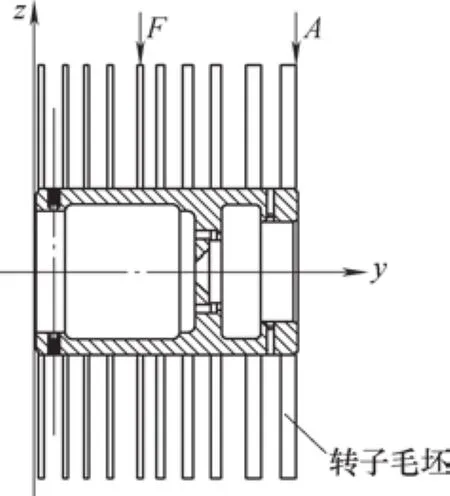
图2　涡轮转子毛坯测量位置简图

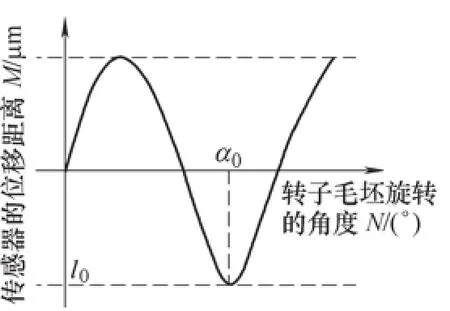
图3　转子中心偏移量曲线

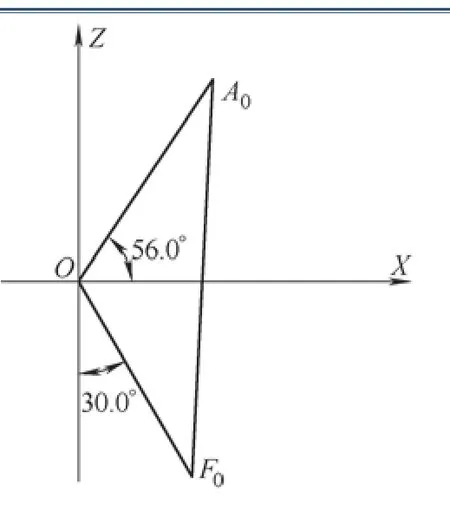
图4　XOZ平面转子轴线位置示意图

设第1层叶片圆心A0与第6层叶片圆心F0在XOZ平面内坐标为A0（x1，z1）、F0（x6，z6）。因为点A0、F0为第1、第6加工层圆心，所以线段A0F0为转子实际轴线，且2、3、4、5加工层圆心均处于轴线A0F0上。由于铣削每层叶片时机床刀具沿转子轴线方向行程较小，与装夹造成的偏差相比较，加工时刀具沿转子轴线方向移动造成X轴及Z轴方向的分量偏差变化较小，在此忽略不计。

计算圆心A0坐标，应用之前所述测量方法可得到转子最大偏心距y0及偏移角度x0，可得方程组

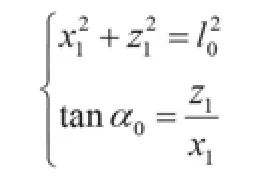
解方程可求出A0（x1，z1）。同理可求出测量点F处第6加工层圆心F0（x6，z6）。

（2）各叶片层圆心的空间坐标变换：建立转子轴线在XOZ平面投影的数学模型

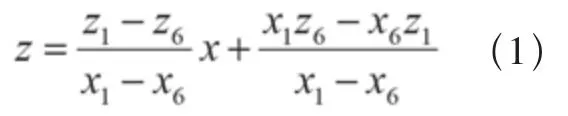
由此转子轴线数学模型可求出在线段A0F0上其他各加工层面圆心的坐标值，并可以矩阵形式表示。以第1层加工面圆心A0点为例，在XOZ平面的矩阵形式为

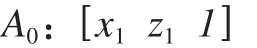
用T来表示二维齐次变换矩阵

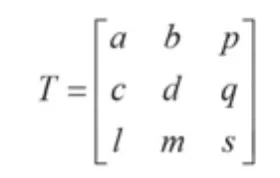
对于涡轮转子，有平移和旋转两种变换。

以第1加工层为例，由于可求出初始位置加工面圆心坐标A0(x1，z1)，所以平移变换矩阵为

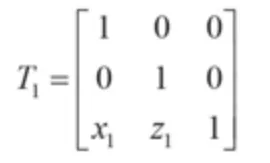
旋转变换矩阵

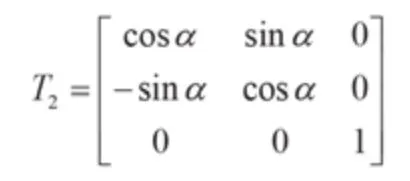
式中，α为转子毛坯旋转角度。

涡轮转子的空间坐标变换矩阵

设点A'为经平移旋转变换后转子加工平面圆心的坐标，由式（2）可知其计算过程为

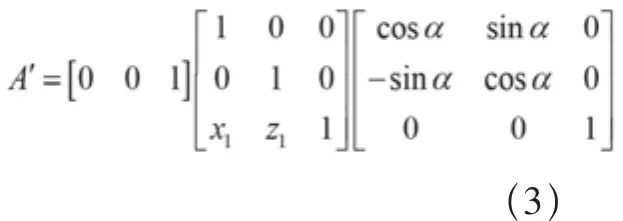
同理，可以利用此变换矩阵算法求出转子毛坯上每一加工层圆心在任意加工位置坐标。

图5所示为上述转子测量及坐标变换计算流程，利用传感器输出的位移信号拟合位移曲线，至少测量两处加工层圆心，根据其位移曲线建立转子轴线的数学模型，确定转子空间位置，由于每一加工层圆心都在转子轴线上，所以可通过变换矩阵计算出每层圆心偏差。

图5　测量及计算流程图

3. 实际加工算例

设分子泵转子装夹后初始位置第1、第6加工面圆心在YOZ平面坐标分别为A0(x1，z1)、F0(x6，z6)。

应用上述方法测量转子装夹偏差。在第1加工层A测量位置得到结果为：α0=56º，l0=52μm；在第2加工层B测量位置得到结果为：α0=300º，l0=52μm。

求第1层加工面圆心A0点坐标，将测量结果代入方程组

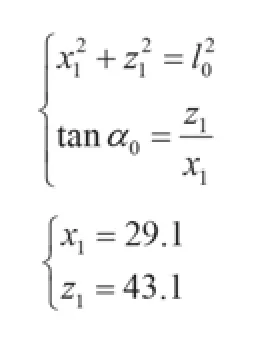
可确定第1层圆心A0点坐标为

A00：（x1z1）=（29.143.1）

同理可求出第6层圆心F0点坐标为

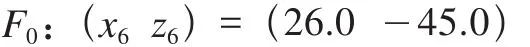
将两加工面圆心A0、F0连接，A0F0为转子的实际轴线，投影到机床的XOZ平面上（见图4），转子2、3、4、5层加工平面圆心均处于轴线A0F0上。线段A0O、F0O分别为第1层加工面与第6层加工面的最大偏心距。根据式（1）建立轴线A0F0在XOZ平面的数学模型

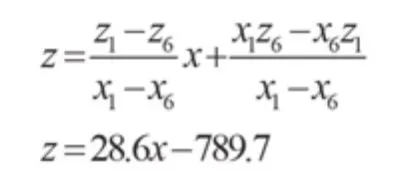
基于以上数学模型，转子2、 3、4、5层加工面：圆心B0、C0、D0、E0初始坐标均可求出

B0点坐标b：（x2z2）=（28.4 22.4）

C0点坐标c：（x3z3）=（27.6 -0.4）

D0点坐标d：（x4z4）=（26.9 -16.7）

E0点坐标e：（x5z5）=（26.4 -33.1）

基于已求出的各圆心坐标可确定各加工平面的平移变换矩阵。由于机床定位精度为2μm，所以各加工平面圆心坐标及平移变换矩阵单元精确到2μm。

以第1加工层面平移变换矩阵为例

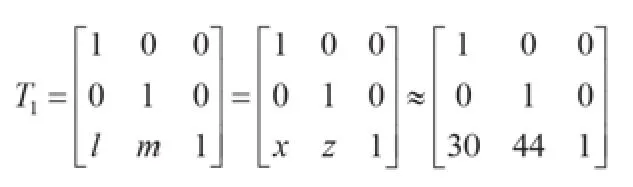
求旋转变换矩阵，由于涡轮转子每层叶片个数不同，所以加工完一片叶片后，分度盘旋转至下一加工位置的旋转角度也不同，基于已知条件，可以计算出分度盘每次旋转的角度

式中，α为分度盘旋转角度；m为分度盘旋转次数；n为加工层转子叶片数。

利用之前所述方法可求出旋转变换矩阵

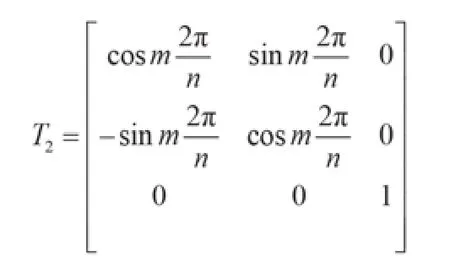
根据式（3）可求出第1层加工平面圆心经一次旋转的计算过程为

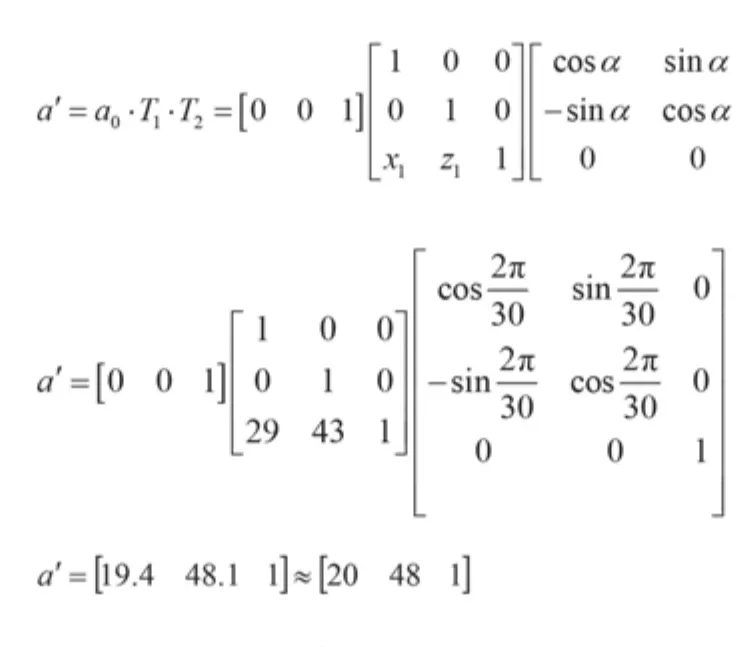
由计算结果可知，涡轮转子第1加工层圆心经过分度盘一次旋转后在XOZ平面上的坐标为（20，48），应用此种坐标变换算法可求出各加工平面上任一加工位置的平面圆心坐标。

图6所示为第1加工层面各加工位置x轴坐标及z轴坐标与机床分度盘旋转角度的曲线关系，横轴为分度盘旋转角度，纵轴为偏移距离。

转子第6层加工面有50片叶片，即加工时分度盘需旋转50次。图7所示为第6层各加工位置圆心x轴及z轴坐标与机床分度盘旋转角度的曲线关系。

基于上述偏移圆心的坐标，利用编制的中间转换器，一次性计算各加工位置的偏移量并修正原有数控加工程序，最终实现自寻位数控加工的目的。

4. 结语

硬铝合金整体涡轮转子是影响分子泵性能的关键部件，基于上述测量及坐标变换方法并配合中间转换器可实现涡轮转子的自寻位数控加工，从而减少工人操作经验对转子加工精度的影响，提高转子产品的生产效率及批量稳定性，在生产中具有一定的实际意义。

参考文献：

[1] 毛德柱，周凯，张伯鹏，等. 智能寻位加工技术应用研究 [J]. 制造技术与机床，2000（4）：42-44.

[2] 胡占齐，张一同，武琳璞，等.基于计算机视觉的凸轮磨削自动定位及在线检测[J]. 中国机械工程，2007，18（18）：2195-2197.

[3] 杨莉，胡占齐. 数控加工中工件的自动定位[J]. 制造技术与机床，2001（4）：23-25.

[4] 崔科. 超大法兰自寻位加工技术的研究[D]. 哈尔滨：哈尔滨工业大学，2007.

[5] 周凯，毛德柱，张伯鹏. 自寻位数控机床的研究[J]. 机械工程学报，2001，37（5）：48-52.

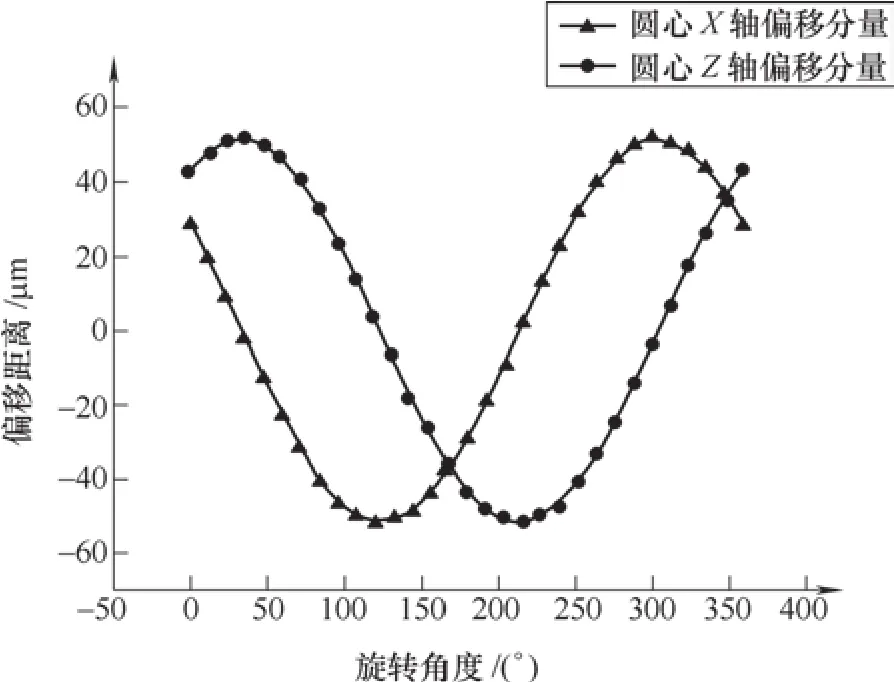
图6　第1层面圆心XOZ平面偏移分量曲线

收稿日期：（20140915）