一种改进的基于预测误差扩展的可逆水印算法

张润生，祁 燕，刘丽萍

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

一种改进的基于预测误差扩展的可逆水印算法

张润生，祁 燕，刘丽萍

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

提出一种具有低失真特点的可逆数字水印算法。通过扩展像素预测值将水印数据嵌入到原始图像中，可在提取水印后准确恢复原始图像。针对传统预测算子不够精确，提出了一种新的具有根据上下文自适应预测能力的预测器，以提高预测精度；并将排序的思想应用到算法中，减小了含水印图像的失真度。实验结果表明，自适应预测器能有效提高预测精度，利用该算法嵌入数据后，水印具有良好的不可见性，在提取水印后能无损地恢复原始图像。

预测误差；可逆；自适应；数字水印

数字水印技术是一种保护图像安全的有效手段，它将一些信息隐藏在图像中，传统的数字水印算法中，在提取水印的同时会对宿主图像造成不可逆的损害，这在卫星遥感、军事、医学等对图像保真度要求极高的特殊领域是不可接受的。如果可以在提取水印的同时无损地恢复原始图像，这种技术则称为可逆数字水印技术，该类水印属于脆弱性水印。

Tian首次提出基于像素差值扩展的可逆数字水印算法[1]。该算法利用Haar整数小波变换具有可逆性，可以将已嵌入的水印信息提取出来并恢复原始载体图像。Thodi等人首次提出了基于预测误差扩展的可逆数字水印算法[2]。该算法选取一个相对简单的预测算子对图像内的像素值进行预测，将预测误差扩展后嵌入水印。相较于差值扩展算法该算法在嵌入容量和图像保真度方面都有较大提升。熊志勇等人提出将Tian差值扩展的技术应用到彩色图像中[3]。Sachnev等人提出了一种四领域预测算子，选取相邻的四个像素对当前像素预测，利用预测误差嵌入水印[4]。Jung的算法在嵌入信息前搬移了载体图像的直方图[5]。以上算法在预测精度上虽有改善，但对于内容变化较大的图像，预测算子仍然不够精确。本文通过分析多种预测算子，提出一种新的具有自适应能力的预测算子，并将其应用到预测误差扩展算法中，和其他算法相比在嵌入等量的水印数据时，图像的失真度更低，达到了良好的可逆水印效果，并经过实验验证了该方案的有效性和可靠性。

1 预测误差差值扩展

1.1 差值扩展

文献[1]提出的差值扩展算法是对两个相邻像素之间差值进行扩展，将水印嵌入到扩展后差值的最低位，嵌入和提取的可逆变换如下：假设a、b是宿主图像的两个邻近像素的灰度值，a、b是整数且0≤a，b≤255。首先计算a、b差值h和平均值l。

(1)

然后在h中嵌入1位数据i，i=0或1：

h′=2h+i

(2)

最后用逆变换求出扩展后的像素值a′，b′：

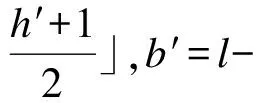
(3)

1.2 预测误差扩展

针对差值扩展算法中嵌入容量较小，一次扩展中一个像素对仅能嵌入1bit水印数据，因此该水印算法只有0.5 bpp的容量上限。根据相邻像素的相关性，可以用邻近的像素的灰度值来预测当前像素的灰度值，以此得到一个当前像素的预测值，当前像素值和预测值的差就是预测误差。Thodi提出的基于预测误差扩展的可逆水印算法是对预测误差进行差值扩展，理论上一个像素一次扩展能嵌入1 bit数据，具有1 bpp容量上限。若假设像素的预测值为I’(i，j)则预测误差p为

p=I(i,j)-I′(i,j)

(4)

该算法预测误差扩展并嵌入1位数据i，i=0或1，嵌入公式为

p′=2p+i

(5)

那么嵌入后的像素值I0为

I0=I(i,j)+p+iI0∈[0,255]

(6)

提取嵌入信息i时：

i=p′-2⎣p′/2」

(7)

恢复原始的预测误差p和像素值I(i，j)

p=⎣p′/2」,I(i,j)=I0-p-i

(8)

1.3 预测算子

在预测误差算法中，预测算子越准确，预测误差就越小，宿主冗余就能利用的更加充分，算法也因此具有更好的性能。

1.3.1Thodi预测算子

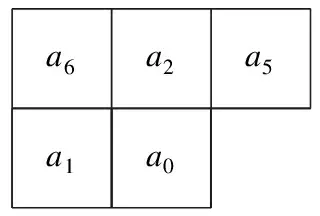
a6a2a5a1a0

图1 预测模板

Thodi提出的预测误差差值扩展算法中，利用周围像素对当前像素值预测，对图像中要预测的像素I(i，j)像素值定义为a0，周围像素值分别为a1、a2、a5、a6，如图1所示，像素预测方法如式(9)。

(9)

该预测算子中只根据a1、a2、a6的值对预测，而忽略了周围的其他像素，如果a0和其他像素较为接近，如图2、图3所示，三角形代表和a0比较接近的区域，如果继续采用该预测算子会对预测值造成较大的误差，影响预测精度。

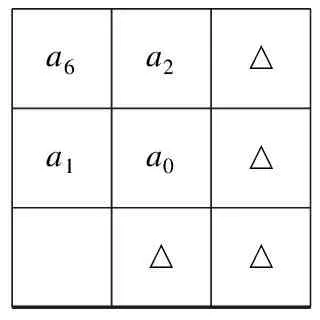
a6a2△a1a0△△△

图2a0和右边像素值较为接近

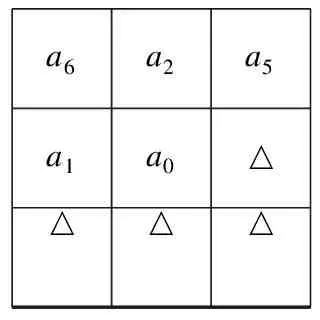
a6a2a5a1a0△△△△

图3a0和下边像素值较为接近

1.3.2 本文预测算子

针对以上不足，本文采用一种自适应的预测方法，充分考虑到不同图像的差异和同一图像中不同位置的差异，利用图像中相邻像素的内在联系更精确地预测初始像素值，像素示意分布如图4所示。

a6a2a5a1a0a3a8a4a7

图4 像素分布示意图

如图要预测像素I(i，j)像素的值为a0，预测值为I′(i，j)，a1～a8均为像素点I(i，j)周围像素的值。Dh、Dv、Dd、Da为其三个相关联像素对应的均值与a0的差值的绝对值如式(10)，值越小说明预测值与实际值越接近，预测误差越小，嵌入水印后失真度越小。相对应预测算子如式(11)。

(10)

1.3.3 两种预测算子比较

用两种预测算子对分别计算lena图像前1000个像素的预测误差p。如图5所示，图5a表示测试的lena图像，图5b、图5c分别代表本文预测算子和Thodi预测算子所得到的预测误差p的值，预测误差p是指预测像素值与原始像素值的差，所以p值越小越好，即越接近于0越好。从图5b、图5c中可以看出，本文提出的预测算子计算出的预测误差在0值附近分布更加集中，本文算法中的预测误差明显要比Thodi算法中的预测误差小，预测精度更高，预测值更接近原始值。

(11)

1.4 像素平滑度值排序

局部图像越平滑，相关像素间差值越小，预测误差值越小；局部图像越粗糙，相关像素间差值越大，预测误差越大[4，6]。优先选取图像中较为平滑的区域进行水印嵌入可有效减小图像的失真，为此，构造平滑度近似度量函数为ρ(x)，像素分布如图4所示，假设计算a0的平滑度值，ρ(x)计算公式为式(12)，对ρ(x)的值进行升序排列，在排列后像素点中嵌入水印可有效地降低图像失真度。

(12)

以图5a的lena图像为实验对象，对其进行像素值预测，并依据ρ(x)值排序，由于篇幅有限只展示部分结果如图6所示，第1列为ρ(x)的值，第2列为预测误差，第3列为预测值，第4、5列分别为该像素值在图像中对应的行和列。

(a)lena图像

(b)本文预测算子得到的预测误差

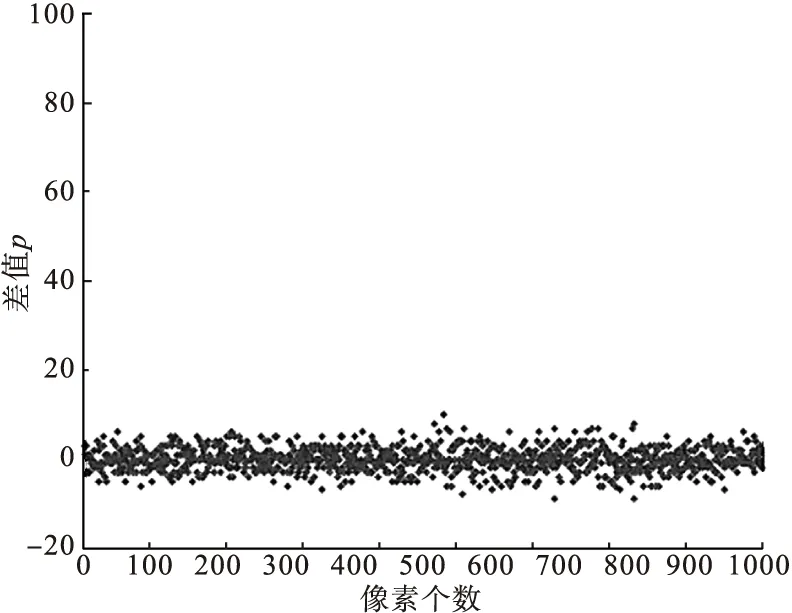
(c)Thodi预测算子得到的预测误差

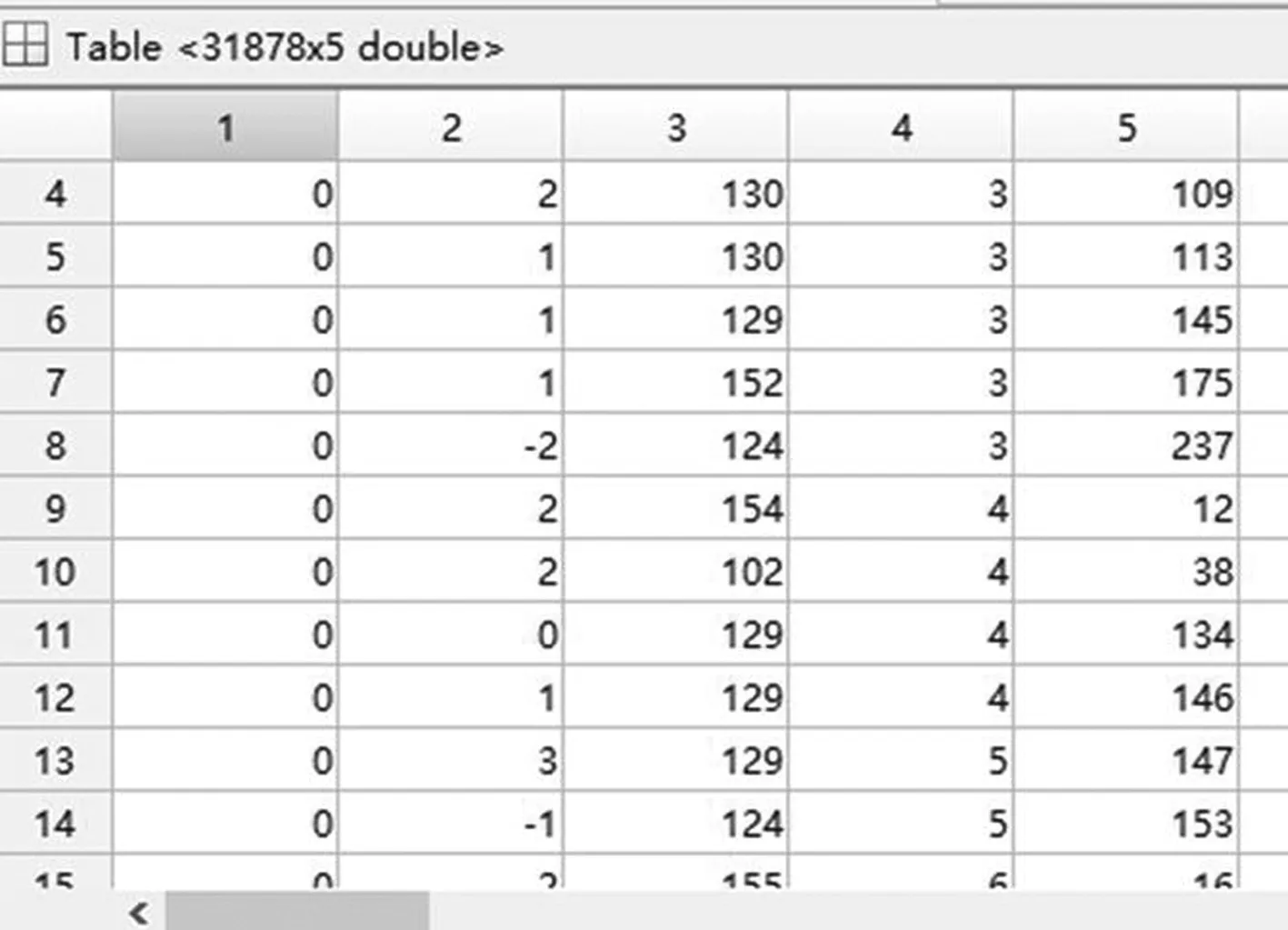
图6 像素值排序结果示意图

1.5 直方图平移

为使图像失真在特定的嵌入量时尽可能低，本文采用直方图平移技术[7]。根据水印嵌入量大小确定阈值T1、Tr，把直方图划分为内部区域和外部区域。内部区域为p∈[T1，Tr]所对应的差值，差值p∈[T1，Tr]时且扩展用式(13)扩展后满足式(6)条件的则成为可扩展区域，而外部区域[-p，T1-1]和[Tr+1，p]的用式(13)扩展后满足式(6)条件的称为可移动区域，该区域差值沿横轴向外侧平移，以避免扩展后的内部区域和外部区域重叠。

水印嵌入时误差p根据不同的范围做如下变换：

(13)

恢复时是变换的逆过程根据式(14)、(15)恢复误差p和水印数据i：

(14)

i=p′-2⎣p′/2」 ifp′∈[2T1,2Tr+1]

(15)

2 嵌入和提取算法

2.1 水印嵌入过程

本文所采用水印为随机生成的二值数据，具体嵌入过程如下：

(1)对宿主图像中每一个像素进行下列操作：

a)用式(10)、(11)计算该像素的预测值I′(i，j)；

b)用式(4)计算预测误差p；

c)用式(12)计算平滑度值ρ(x0)。

(2)对所有像素根据ρ(x0)值的大小进行升序排序，并收集序列的前34个像素的最低位组成序列Slb，并将Slb和要嵌入的水印信息归入有效负载V中；

(3)根据嵌入水印的多少计算合适的T1、Tr的值；

(4)根据V的大小将宿主图像的像素点分为可扩展类区间和可移动类区间，并且生成一个相应的位置图，位置图长度为L，其中可扩展类区间包含像素的总个数用E表示。从像素序列的第35个像素开始，对每一个像素进行如下计算：

a)如果该像素点扩展后没有溢出且属于可扩展区间，相应的位置图标记为0，否则标记为1；

b)判断是否已找到足够的嵌入空间，如果V+L<=E则进行步骤(5)，如果当前为最后一个像素且V+L>E，则调整T1、Tr的值，重复第(4)步；

(5)将有效负载V和位置图嵌入载体图像中；

(6)将T1、Tr以及有效负载V的长度嵌入前34个像素点的最低位；

(7)计算嵌入数据后的图像的像素值，获得一个嵌入水印信息后的图像。

2.2 水印提取和图像恢复过程

水印提取是水印嵌入的一个逆过程，不需要原始图像，提取端需要三个参数，T1、Tr的值，有效负载V的长度。

(1)参照嵌入过程的第一步，计算出预测值，预测误差及平滑度值；

(2)根据ρ(x0)值对像素点按升序排列，提取前34个像素点的最低有效位，恢复T1、Tr以及负载V的长度；

(3)依据T1、Tr将像素点分为可扩展类区间和可移动类区间；

(4)根据直方图平移原理计算出初始的预测误差p，位置图的长度L，以及有效负载V。将Slb从V中分离出来；

(5)利用式(8)、(14)、(15)恢复原始像素值；

(6)根据Slb恢复前34个像素的最低有效位。

3 实验结果

本节通过实验对算法进行验证，实验环境为Matlab 2012，测试图像为256×256的lena灰度图像如图5a所示，水印数据随机产生。水印嵌入容量为0.9bpp时，图像含水印图像与初始图像分别为图7a和图7b，图像嵌入水印前后同一位置的部分像素值变化如图8所示，图8a表示初始图像中的部分位置的像素值，图8b表示含水印图像中部分位置像素值。

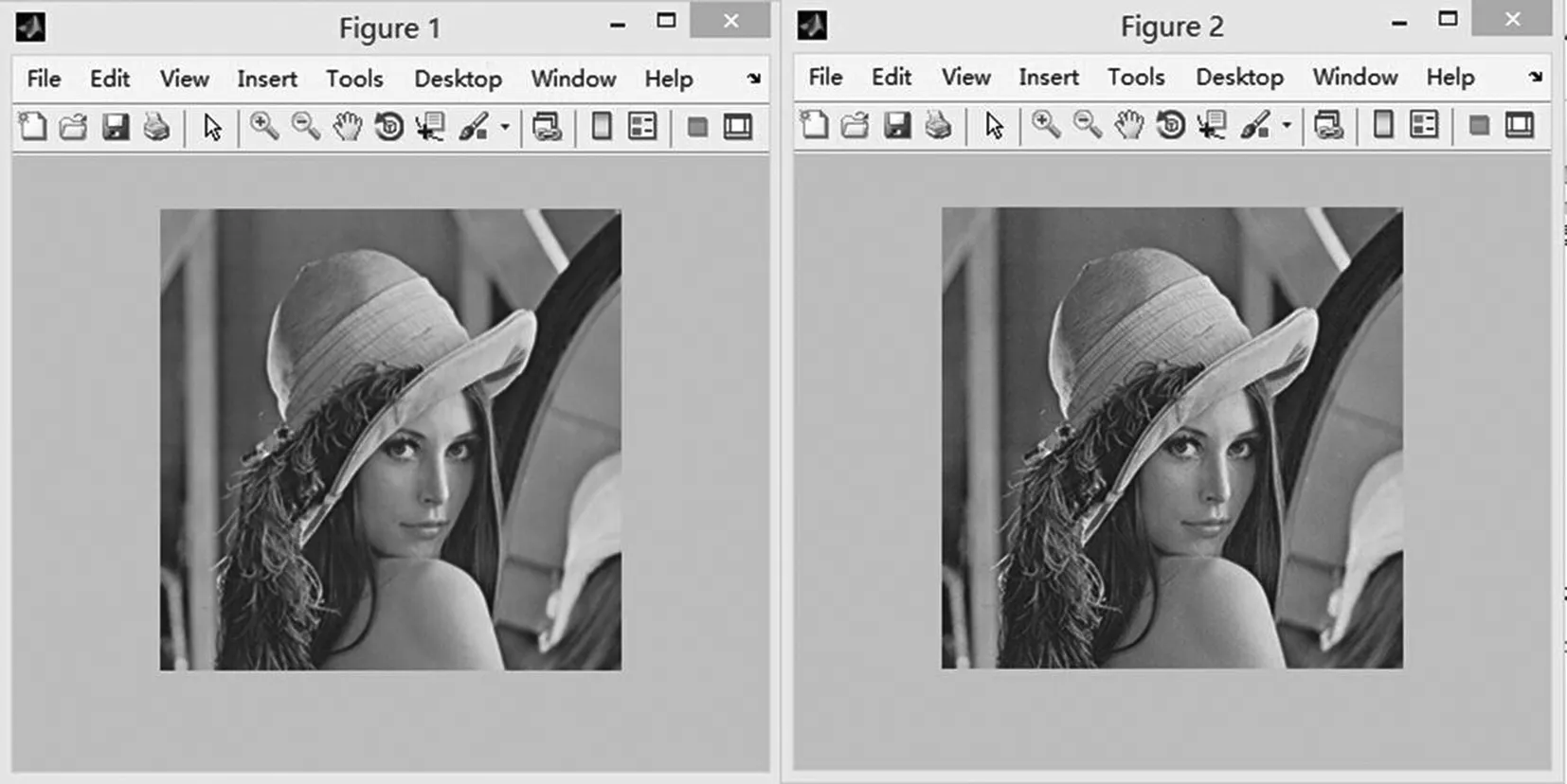
(a)原始图像 (b)含水印图像

(a)初始图像部分位置像素值

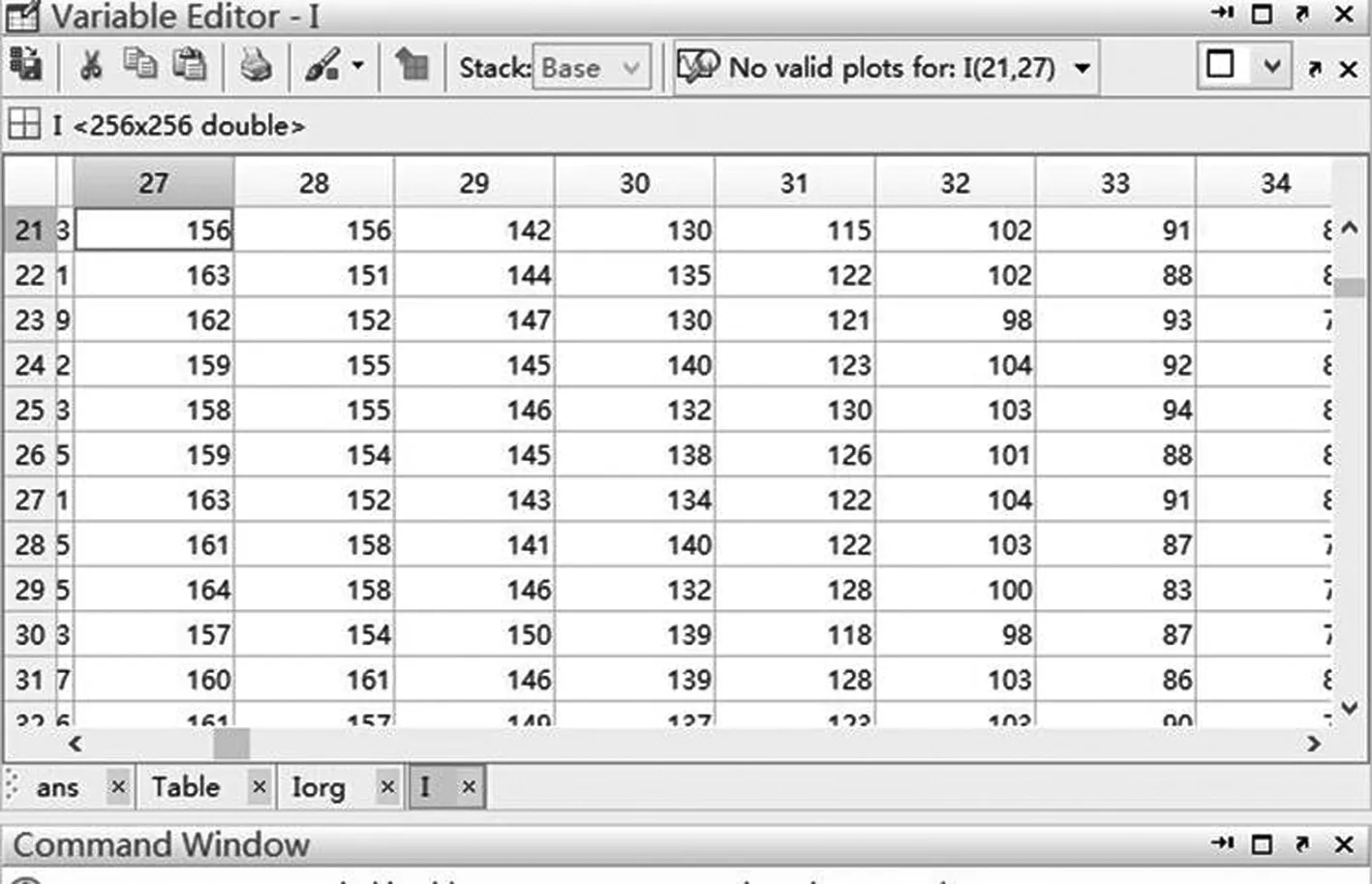
(b)嵌入水印后该位置像素值

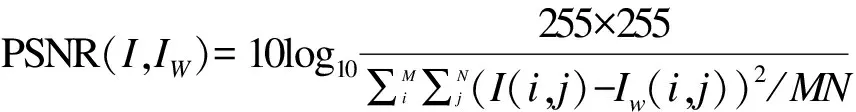
(16)

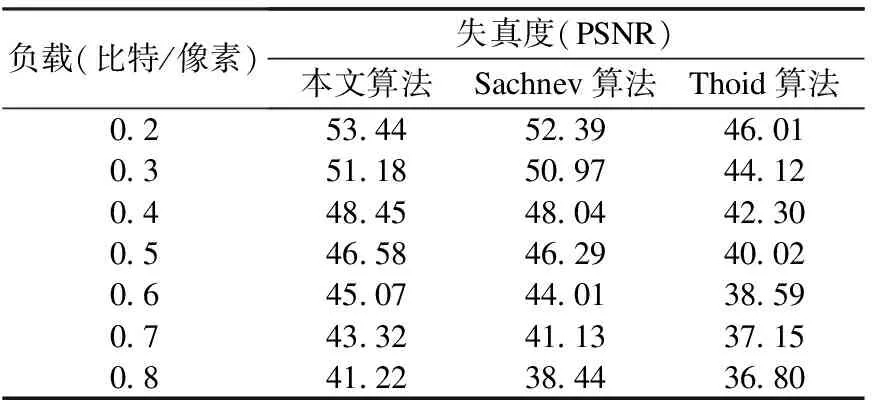
表1 lena图像不同的算法嵌入容量和失真度对比

测试lena图像采用不同算法嵌入水印时嵌入容量与峰值信噪比的曲线对比如图9所示。从图9中可以更加直观地看出，本文算法优于Sachnnev和Thodi提出的算法。

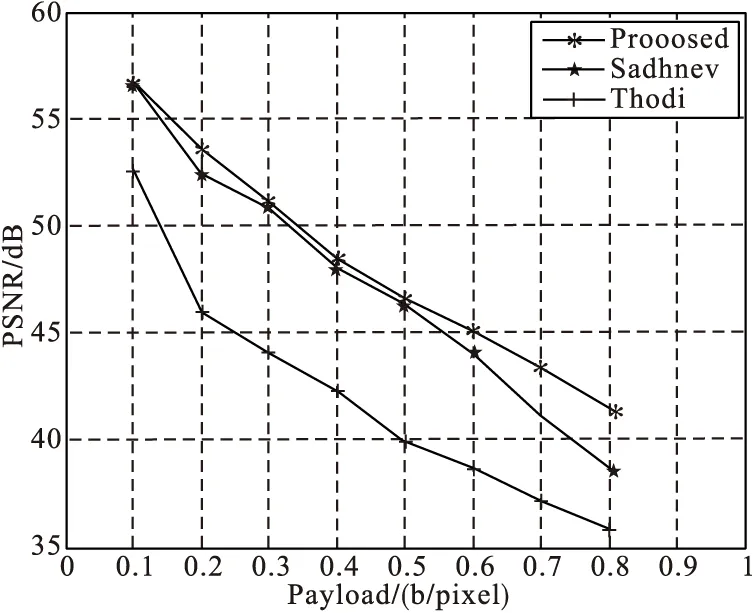
图9 嵌入容量与峰值信噪比对比图

4 结束语

针对以往的预测误差扩展算法中过分利用预测误差而导致预测精度不高的缺点，提出一种基于排序和自适应预测的可逆水印算法。本文算法根据嵌入水印容量的大小，有选择地确定阈值T1、Tr；自适应地对当前像素值进行预测，使预测值更加接近原始值；寻找平滑区域，并依据当前像素点的特征值对其排序，嵌入水印后有效地减小了图像失s真。实验结果表明，该算法在保证图像质量的同时，能够无损地恢复原始图像。

[1]Tian J.Reversible data embedding using a difference expansion[J].IEEE Trans on Circuits and Systems for Video Technology，2003，13(8)：890-896.

[2]Thodi D M，Rodriguez J J.Prediction-error based reversible watermarking[C].Proc of Int Conf on Image Processing.Piscataway，NJ：IEEE，2004：1549-1552.

[3]熊志勇，蒋天发.基于预测误差差值扩展的彩色图像无损数据隐藏[J].计算机应用，2010，30(1)：186-200.

[4]Sachnev V，Kjm H J，Nam J，et al.Reversible watermarking algorithm using sorting and prediction[J].IEEE Transact Circults and Systems for Video Technology，2009，19(7)：989-999.

[5]Jung，Le Thanh Ha，SJ Ko.A new histogram modification based reversible data hiding algorithm considering the human visual system[J].IEEE Signal Processing Letters，2011，18(2)：95-98.

[6]常志国.可逆水印与图像技术保护研究[D].上海：上海交通大学，2009.

[7]Thodi D M，Rodriguez J J.Expansion embedding techniques for reversible watermarking[J].IEEE Transaction on Image Processing，2007，16(3)：721-730.

(责任编辑：马金发)

An Improved Reversible Watermarking Algorithm Based on Prediction Error Expansion

ZHANG Runsheng,QI Yan,LIU Liping

(Shenyang Ligong University,Shenyang 110159,China)

A watermark hiding algorithm is proposed with low distortion.This algorithm employs prediction errors to embed watermark into an image.The original image can be exactly recovered after the embedded watermark is extracted.In view of the fact that the traditional prediction errors are not too accurate,a new method is presented to use other neighboring pixels to predict the present pixel value.The algorithm adopts a sorting technique to embed data with a low distortion.The experimental results indicate that the auto predict method can improve the prediction accuracy which can embed date with low distortion.The original host image can still be recovered after the hidden watermark is extracted.

prediction error;reversible;auto;watermarking

2014-11-07

辽宁省教育厅科学研究一般项目(L2014077)

张润生(1990—)，男，硕士研究生；通讯作者：祁燕(1978—)，女，副教授，研究方向：数字图像处理.

1003-1251(2015)04-0084-06

TP391

A