用于低功耗的体域网加速度数据压缩感知设计

吴建宁 徐海东 王 珏

1(福建师范大学数学与计算机科学学院，福州 350007)2(西安交通大学生物医学信息工程教育部重点实验室，西安 710049)



用于低功耗的体域网加速度数据压缩感知设计

吴建宁1*徐海东1王 珏2

1(福建师范大学数学与计算机科学学院，福州 350007)2(西安交通大学生物医学信息工程教育部重点实验室，西安 710049)

为有效降低体域网加速度数据远程获取系统功耗，提出一种用于低功耗的体域网加速度数据压缩感知处理框架。首先基于优化的稀疏二进制测量矩阵，线性投影压缩体域网传感节点的加速度数据，降低相应节点压缩算法的复杂性和数据传输量；在此基础上，基于块稀疏贝叶斯学习模型，构建非稀疏加速度数据压缩感知重构算法，实现低功耗远程获取加速度数据。实验采用USC-HAD数据库的加速度数据，评估所提方法的有效性。结果表明，当优化稀疏二进制测量矩阵中每列非零元素个数为6、压缩率为50%时，能够获得与传统优化高斯随机矩阵、伯努利随机矩阵相同的压缩重构误差(约0.004 5)；与一些传统的压缩感知重构算法相比，所提出的重构算法提高信噪比约17 dB，显著改善重构性能，可有效实现低功耗远程获取加速度数据。该方法有助于传感节点硬件简化设计，改善加速度数据重构性能，为构建低功耗体域网人体活动远程监测系统提供新的思路和方法。

压缩感知；低功耗；加速度数据；体域网；远程医疗

引言

基于MEMS加速度传感器构建的体域网(wireless body area networks)人体活动远程监测系统，具有低成本、便携穿戴和易操作等优点，近年来在远程医疗和康复等领域受到广泛关注和应用，成为临床诊断的有效辅助技术手段[1-2]。目前，针对远程医疗和康复应用环境，大部分体域网人体活动远程监测系统架构主要由体域网加速度传感节点采集系统、数据传输系统、远端数据处理系统三部分组成，其功能主要实现加速度数据采集、传送，为远端数据处理系统提供可靠数据，用于后续医疗和康复评价。在实际应用中，传感节点通常佩戴于人体的相关部位上，用于采集和传送加速度数据。由于传感节点自带电池能量有限，难以为远端数据处理系统提供长时间连续的监测数据，影响后续医疗、康复评价效果。基于低功耗传感节点准确获取远程生理数据，已是当前体域网人体活动远程监测系统在远程医疗实际应用中急需解决的关键问题。

相关研究发现，为便于人体佩戴、数据采集和传送，加速度传感节点硬件系统通常由加速度传感采集模块、微控制处理器模块、无线发送模块、电源模块组成，其能量主要消耗于数据采集、数据模数转换、程序代码运行和传输数据等方面，其中反复传输数据将消耗大部分能量。为有效降低传感节点功耗、准确传输数据，数据压缩方法在近年来相关领域研究中受到广泛关注，其基本思路是：首先，将体域网远程监测系统获取数据处理分为数据压缩、数据重构两个阶段，也就是在体域网传感节点压缩数据，旨在尝试减少传感节点数据传输量，降低其功耗；其次，在远端数据处理系统构建数据重构算法，尝试准确恢复原始数据，为后续医疗、康复评价提供可靠数据。近年来，一些学者针对数据非平稳性，应用小波分析技术压缩、重构体域网远程监测系统加速度数据，尝试寻找传感节点低功耗、准确获取数据的有效方法。研究发现，为有效实现计算复杂的小波压缩、重构算法，需为传感节点微控制处理单元配置相应的存储器，使其硬件系统设计复杂、功耗增加，难以在实际应用中推广和应用。目前，探寻计算复杂性低且有助于改善传感节点硬件系统简化设计的数据压缩方法，是国内外相关学者探讨的热点问题[3-4]。

近年来，一种不同于传统数据压缩算法的压缩感知(compressed sensing)框架算法在国内外相关研究领域受到极大关注和重视[5-7]。该框架算法依据于数据稀疏性，通过选用与稀疏表示数据的稀疏矩阵(sparse matrix)保持最大不一致性(incoherent)的测量矩阵(measurement matrix)，在远低于奈奎斯特采样率情况下，实现数据压缩和重构。在其实现过程中，测量矩阵选取和设计至关重要。目前，压缩感知技术在基于低功耗体域网的远程医疗数据处理研究中受到广泛关注，其研究工作主要集中于两个方面。一方面，集中于探寻有助于传感节点低功耗、硬件简化设计的测量矩阵，尝试寻找有效降低传感节点功耗的新方法。例如，Dixon等学者基于心电(ECG)信号稀疏性，设计了一种动态阈值方法的一位伯努利测量矩阵，尝试采用压缩感知框架提高心电数据压缩率，实现体域网传感节点的低功耗。但研究发现，伯努利测量矩阵计算复杂，不利于传感节点硬件简化设计；未考虑所设计的测量矩阵对压缩数据重构性能的影响，难以在实际应用中推广[8]。另一方面，主要集中于探寻基于体域网生理数据的压缩感知重构新算法，目前的相关研究着重探讨体域网非稀疏生理数据压缩重构新算法，尝试解决传统压缩感知重构算法难以准确重构非稀疏数据的问题。例如，Zhang等提出了基于块稀疏贝叶斯学习的非稀疏生理数据重构算法，旨在有效利用数据块结构内在相关性，寻找数据块结构内在稀疏性，提高非稀疏数据重构性能。研究表明，该算法可有效提高体域网脑电(EEG)数据重构性能，并为其他体域网非稀疏生理数据重构提供新的思路和方法。然而，该研究仅采用高斯随机测量矩阵构建块稀疏贝叶斯学习重构算法，未考虑测量矩阵对传感节点低功耗的影响[9-10]。目前，用于压缩感知框架的测量矩阵主要有高斯随机测量矩阵、伯努利随机测量矩阵、稀疏二进制测量矩阵。从理论上讲，高斯随机测量矩阵和伯努利随机测量矩阵的压缩重构性能优于稀疏二进制测量矩阵。近年来，相关研究较多采用高斯随机测量矩阵或伯努利随机测量矩阵构建压缩感知算法，而未充分考虑稀疏二进制测量矩阵(矩阵仅含元素0和元素1)在体域网传感节点硬件简化设计和低功耗方面的作用。如何在实际应用中优化稀疏二进制测量矩阵，提高压缩感知算法性能，是近年来相关研究的热点问题，其相关研究成果鲜有报道。

本研究尝试基于传感节点硬件和加速度数据的非稀疏特点，提出了一种用于低功耗的体域网加速度数据压缩感知处理框架，其基本思路就是通过优化设计稀疏二进制测量矩阵，在传感节点实现线性投影压缩原始加速度数据，以期降低传感节点功耗；然后基于优化稀疏二进制测量矩阵，构建非稀疏加速度数据块稀疏学习重构算法，以期准确恢复原始加速度数据。本研究采用美国Southern California大学人体运动数据库USC-HAD的加速度数据，评估基于稀疏二进制测量矩阵构建的压缩感知框架的有效性，还与高斯随机测量矩阵、伯努利随机测量矩阵进行比较，进一步评估优化设计的稀疏二进制测量矩阵对加速度数据压缩重构性能的影响，从而为传感节点硬件简化设计、构建低功耗体域网人体活动远程监测系统奠定基础。

1 低功耗体域网加速度数据压缩感知框架

1.1 压缩感知技术

压缩感知是近年来新发展的一个数据压缩处理技术[11]，主要依据数据稀疏性，采用与数据稀疏表示矩阵不同的测量矩阵，实现数据压缩和重构，也就是假设数据x∈RN×1(N为数据长度)可稀疏表示为

(1)

式中，稀疏矩阵Ψ=[φ1,φ2,…,φN]，c为稀疏系数。

数据x通过测量矩阵Φ∈RM×N(M≪N)线性投影, 即

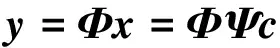
(2)

可得到压缩数据y∈RM×1，有效实现高维原始数据压缩。在数据压缩实现过程中，测量矩阵Φ可根据应用实际情况自行设计。

数据重构是压缩感知技术中的一个重要环节，旨在从压缩数据y∈RM×1中求解出数据x的稀疏系数c，实现数据重构。由于压缩数据长度M远低于重构数据长度N，通过式(2)，难以从已知少数压缩数据变量求解出多数的重构未知变量。为获得重构未知变量，压缩感知理论依据数据稀疏性，对稀疏矩阵Ψ和测量矩阵Φ进行有效约束。

1)矩阵Θ=ΦΨ(Θ∈RM×N)须满足有限等距性质(restrictedisometryproperty,RIP)，也就是对于任意满足稀疏度k的数据x和常数δk∈(0,1)，矩阵Θ满足

(3)

2)稀疏矩阵Ψ和测量矩阵Φ必须保持不一致性(incoherent)，即测量矩阵行向量φi不能稀疏表示稀疏矩阵列向量φj，其定义如下：

(4)

为此，将压缩感知重构问题转化为从压缩数据y∈RM×1中求解出稀疏系数c=ΨTx，即可将上述数据重构问题转化为求解下列l0范数问题,有

(5)

由于式(5)求解为NP问题，可将求解l0最小范数问题转化为求解最小范数l1问题[12]，即

(6)

1.2 用于低功耗的加速度数据压缩感知设计

1.2.1 优化设计稀疏二进制测量矩阵

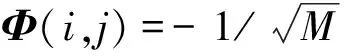
(7)

在两矩阵相乘时，元素0相当于不参与计算，而元素1的运算相当于加法运算。特别地，元素1在矩阵中随机配置，若优化设计稀疏二进制矩阵，使矩阵中每列只有d个元素1，则只需要进行N×d个简单加法运算，这不仅可以降低计算复杂性，而且有助于传感节点数字电路系统优化设计，降低传感节点功耗[7,9-10,13]。研究针对加速度数据非稀疏性，优化设计稀疏二进制测量矩阵，为体域网加速度数据压缩重构奠定基础。

1.2.2 基于BSBL的非稀疏加速度数据重构算法

考虑到加速度数据非稀疏性和稀疏二进制矩阵优化设计特点，研究采用块稀疏贝叶斯学习算法重构非稀疏加速度数据[14]，其压缩感知模型为

y=Ax+v

(8)

式中，感知矩阵A=ΨΦ,A∈RM×N，压缩数据y∈RM×1，噪声v∈RM×1，原始加速度数据x∈RN×1。传统压缩感知重构算法难以准确重构非稀疏加速度数据。为有效提高非稀疏加速度数据重构性能，将加速度数据x划分为l个块结构，即

(9)

式中，hi为第i块大小。

在数据块结构中，仅有少数内嵌块结构为非零元素，大部分块结构为零元素。将上述数据块结构假设为块稀疏结构，利用块稀疏贝叶斯学习算法捕获加速度数据块内在稀疏性，提高非稀疏加速度数据重构性能。假设每个数据块相互独立，均服从多元高斯分布，即

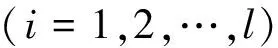
(10)

式中，γi为控制块稀疏参数，若γi=0表示第i块为0；Bi∈Rhi×hi为正定矩阵，用于描述第i块内在元素相关性。

考虑到划分数据块之间非相关，可将加速度数据x的先验分布定义为

(11)

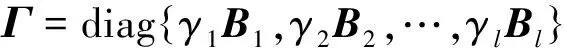
假设噪声v满足独立的高斯分布，即

(12)

式中，β-1>0为一个尺度参数。

假设加速度压缩数据满足多元高斯分布，即

(13)

根据式(11)和(13)，可计算得到加速度数据x的后验分布，有

(14)

压缩数据的后验分布为

(15)

式中，Σ≜(Γ-1+ΦTβΦ)-1,μ≜ΣΦTβy,C≜β-1I+ΦΓΦT。

构建代价函数如下：

(16)

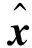
1.3 算法评估

1.3.1 优化稀疏二进制矩阵压缩和重构性能评价

在低功耗加速度数据压缩感知框架中，体域网传感节点能耗与加速度数据压缩率和测量矩阵Φ优化设计密切相关，既要考虑传感节点的低功耗，也要考虑对加速度数据重构性能的影响。在本研究中，优化的稀疏二进制矩阵对低功耗加速度数据压缩感知性能至关重要。为客观评价该优化设计的稀疏二进制测量矩阵对加速度数据压缩重构的性能，将优化设计的稀疏二进制测量矩阵与传统的高斯随机矩阵、伯努利随机矩阵进行比较。

此外，为客观评价本研究所提的重构算法性能，笔者选用了一些传统压缩感知重构算法(如OMP[15]、BasicPursuit[16]、SL0[17]、Elastic-Net[18]、BlockOMP[19]、ClussMCMC[20]、StructOMP[21]等)进行比较。

1.3.2 算法性能客观评价指标

为客观评价基于优化设计稀疏二进制测量矩阵的加速度数据压缩重构算法性能，实验采用了4个观评价指标。

1)压缩率(CR)。用来量化客观评价优化设计稀疏二进制测量矩阵压缩性能，其定义如下：

(17)

式中，N为原始加速度数据长度，M为压缩数据长度。

2)均方根误差(NMSE)。用来量化原始加速度数据与重构加速度数据之间的误差，客观评价加速度数据重构性能，其定义如下：

(18)

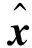
3)信噪比(SNR)。用来量化加速度数据重构误差，客观评价加速度数据压缩感知重构算法性能，其定义如下：

(19)

4)Pearson相关系数(R)。用来量化原始加速度数据与其压缩重构数据的相似度，客观评价加速度数据压缩感知重构算法性能，定义为

(20)

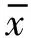
上述算法运行环境为Matlab7.0、Intel(R)Core(TM)i5-3470、3.20GHzCPU和4.00GBRAM。

2 结果

2.1 加速度数据采集

本研究采用美国Southern California大学人体步态运动数据库(USC-HAD)的加速度数据(http://www-scf.usc.edu/～mizhang/datasets.html)，以验证上述所提优化设计压缩感知框架的有效性[22]。数据库(USC-HAD)包含14名健康受试者的加速度数据，在采集中，每名受试者佩戴集成加速度计和陀螺仪的传感节点，通过随身携带小型采集设备(motion node)，实时记录人体不同的运动状态数据，采集频率设置为100 Hz，每种运动状态重复采集5次。一名受试者自然行走的三维加速度数据如图1所示。

图1 人体行走状态的加速度数据(X轴为人体运动前进方向； Y轴为人体运动侧向方向； Z轴为人体运动垂直方向)。(a)X轴；(b)Y轴；(c)Z轴Fig.1 Acceleration data with the three-axis directions during human walking(X axis denotes the anterior-posterior direction during human movement; Y axis is the medio-lateral direction during human movement; Z axis represents the vertical direction during human movement). (a) X axis; (b) Y axis; (c) Z axis

2.2 优化稀疏二进制测量矩阵性能评价结果

优化设计稀疏二进制测量矩阵的关键在于选取稀疏二进制测量矩阵每列最少非零元素的个数(用d表示)，实验中选用行走状态X轴加速度数据，数据长度为512。图2给出了依据不同压缩率和重构误差来确定测量矩阵最优d值的实验结果。

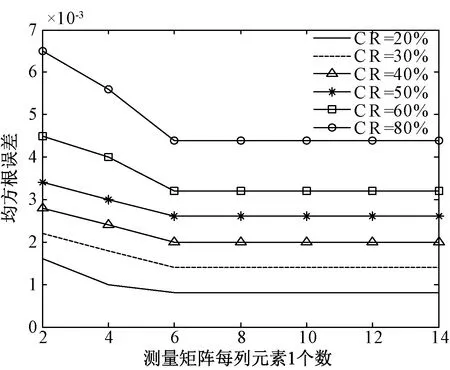
图2 基于不同压缩率的测量矩阵每列元素1个数与重构误差的变化关系Fig.2 The change between reconstruction error and a number of nonzero values selected from the measurement matrix based on different CRs

从图2中可以看到，加速度数据重构误差随着压缩率的增加而增大，但在每个选取的压缩率状态下，加速度数据重构误差随着测量矩阵中d值的增加而迅速下降，当测量矩阵中d=6时，重构误差保持稳定。结果表明，d值选取为6(也就是最优d=6)的测量矩阵，可获得与d>6的测量矩阵相同的重构性能。此外，实验也将优化设计稀疏二进制测量矩阵(d=6)与高斯随机矩阵、伯努利随机矩阵进行比较，进一步评估研究所优化设计的测量矩阵压缩重构性能。在实验中，采用上述相同加速度数据，高斯随机矩阵中每个元素由独立同分布的高斯随机变量形成，伯努利随机矩阵中每个元素由独立同分布的伯努利随机变量形成。实验结果如图3所示，可看出3种不同测量矩阵的重构误差均随压缩率增大而增大。当压缩率在20%～45%变化时，基于3种不同测量矩阵的重构误差基本相同；当压缩率在45%～65%变化时，基于稀疏二进制测量矩阵的重构误差介于高斯和伯努利两个随机矩阵重构误差之间；当压缩率在70%～80%变化时，稀疏二进制测量矩阵重构误差大于高斯和伯努利两个矩阵重构误差。结果表明，次优化稀疏二进制测量矩阵通过优化设计，也可获得与高斯随机测量矩阵、伯努利随机测量矩阵几乎相同的压缩重构性能。

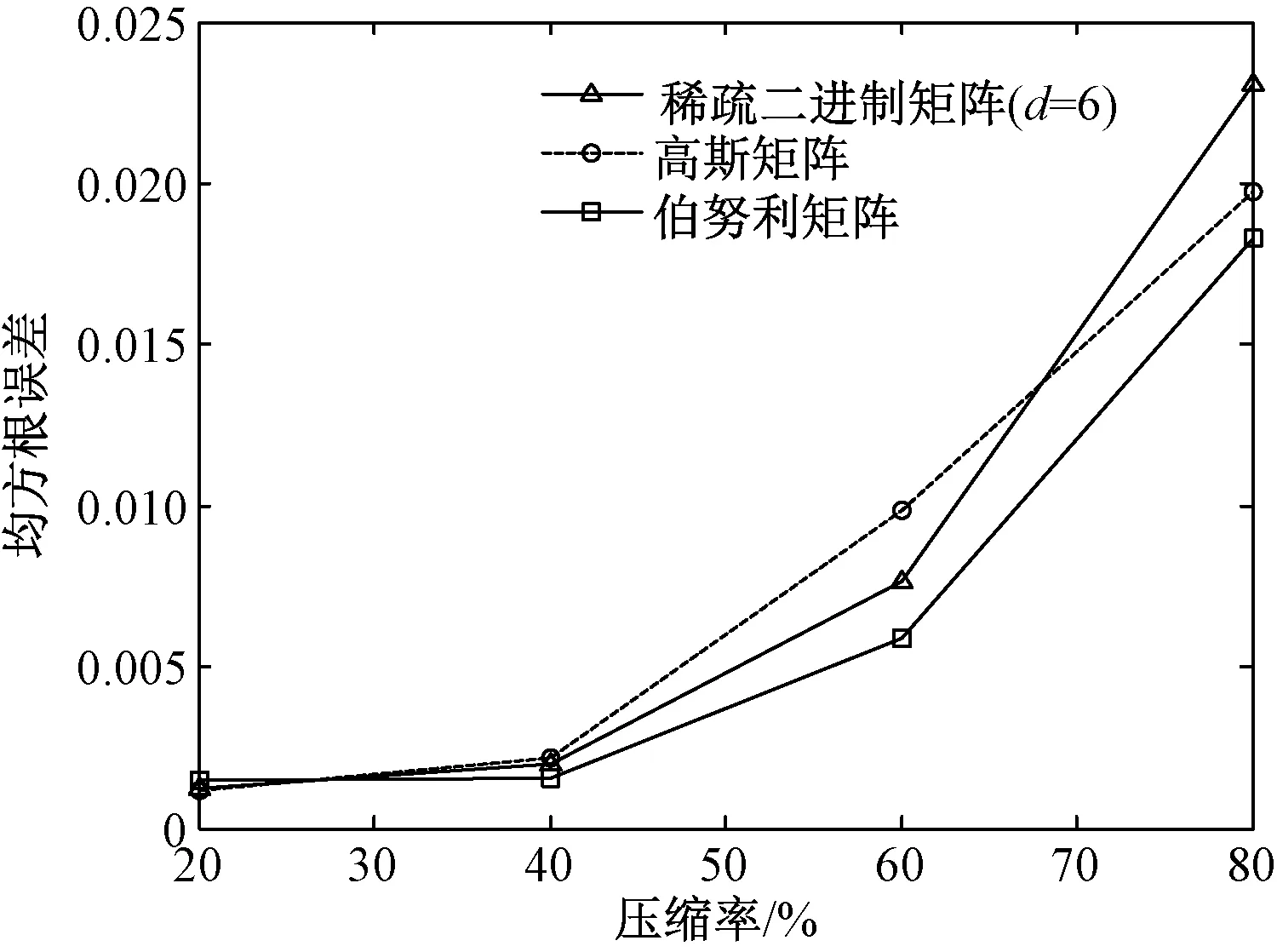
图3 基于不同测量矩阵的压缩率与重构误差的变化关系Fig.3 The relationship between the reconstruction error and the ratio of compression in the selected measurement matrixes

另外，实验也分别采用信噪比(SNR)和Pearson相关系数评估稀疏二进制测量矩阵d值变化对加速度压缩数据重构性能的影响，实验结果如图4、5所示。

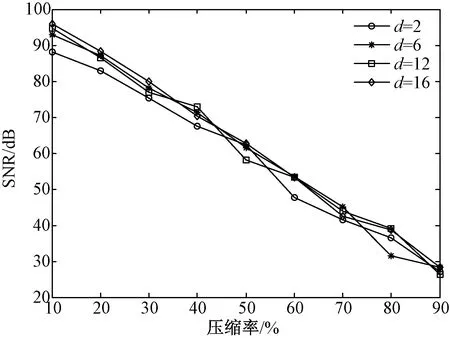
图4 基于测量矩阵不同值的重构算法信噪比与压缩率的变化关系Fig.4 The relationship of change between the SNR from reconstruction algorithm and the CRs based on the different d in the measurement matrix

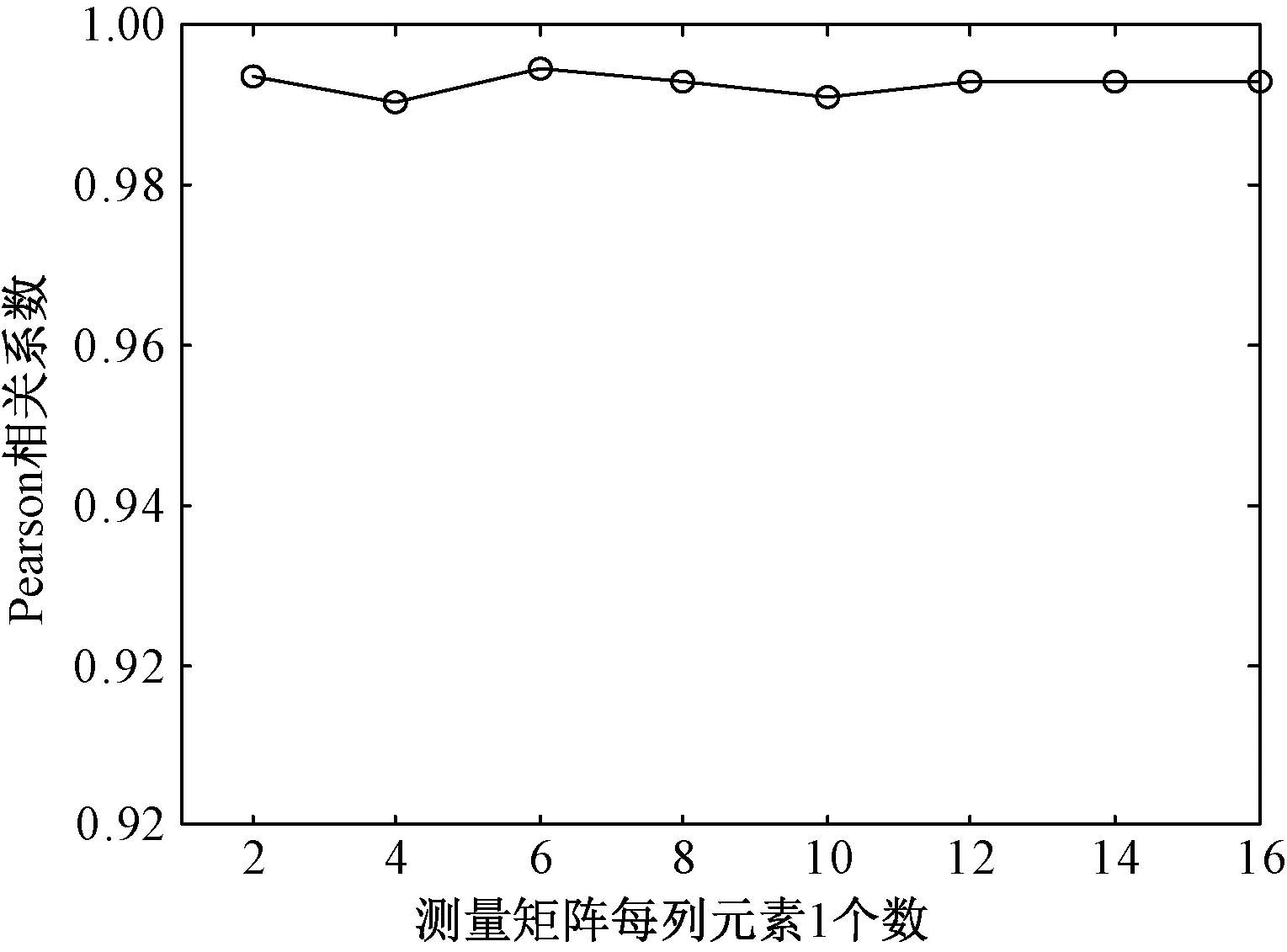
图5 Pearson关联系数与d选取的变化关系Fig.5 The relationship of change between the R and the different values of d selected

从图4中可以看到，当稀疏二进制测量矩阵d值分别选取2、6、12、16时，加速度数据重构算法信噪比均随压缩率的增加而降低。在相同压缩率情况下，基于不同d值的重构算法信噪比均较接近。比较而言，基于d=6的信噪比随压缩率的变化较平稳，波动较小。结果表明，在稀疏二进制测量矩阵d值的变化过程中，数据高压缩率必将影响压缩数据重构性能。在优化选取d值时，需折衷考虑数据压缩率与其重构性能之间的变化影响。

图5给出了重构加速度数据Pearson相关系数R与稀疏二进制测量矩阵不同d值的变化关系。由于稀疏二进制矩阵中元素1的位置随机变化，可能导致重构加速度数据与原始加速度数据之间的Pearson相关系数存在差异。为减少差异，实验中Pearson相关系数R取20次重构平均值。从图5中可以看到，平均R值均大于0.99，其变化差异为0.003 0，d=6时R为最大值(0.994 5)。结果表明，随着稀疏二进制测量矩阵值的变化，重构加速度数据Pearson相关系数基本保持在一个稳定的范围内，对加速度数据重构性能影响较小，有助于降低传感节点计算开销，降低其功耗。

2.3 重构算法性能评价结果

实验选取加速度数据长度为512，压缩率为50%，稀疏二进制测量矩阵为256×512(测量矩阵中每列元素1个数为6(即d=6)，数据块划分长度为24。基于不同重构算法的比较结果如表1所示，从中可以发现，在相同压缩率(50%)情况下， 本研究所提出的重构算法信噪比最大(SNR=57.955 6)，明显高于其他传统压缩感知重构算法的信噪比，表明基于优化稀疏二进制测量矩阵构建的块稀疏贝叶斯学习重构算法能够捕获非稀疏性加速度数据块内在稀疏性，有效改善非稀疏数据重构性能。但是，本研究所提的重构算法的重构时间(1.825 0s)低于其他一些传统压缩感知重构算法的重构时间，这可能是由于块稀疏贝叶斯学习算法需要花费稍多的迭代时间来捕获加速度数据内在块稀疏性。

表1 不同重构算法的加速度数据重构性能对比

Tab.1 The results of comparative performance of the different reconstruction algorithm for acceleration data

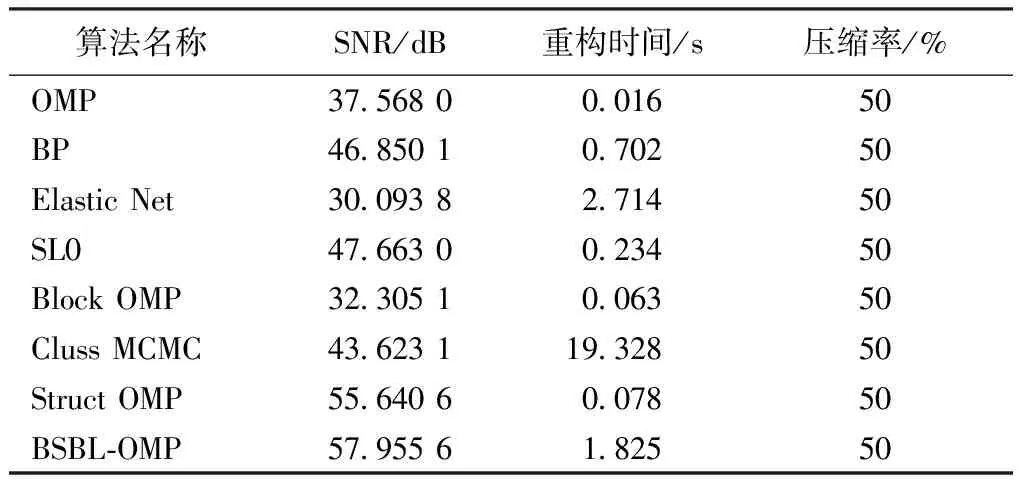
算法名称SNR/dB重构时间/s压缩率/%OMP375680001650BP468501070250ElasticNet300938271450SL0476630023450BlockOMP323051006350ClussMCMC4362311932850StructOMP556406007850BSBL⁃OMP579556182550

3 讨论

实验结果表明，基于优化稀疏二进制测量矩阵构建的体域网加速度数据压缩感知框架，能够有效降低传感节点功耗，准确重构加速度压缩数据，为低功耗体域网传感节点硬件简化设计、远端数据处理系统准确获取数据提供了可靠技术支撑。目前，基于低功耗传感节点准确获取远程生理数据，一直是国内外相关学者致力研究的热点问题。虽然数据压缩方法为解决上述热点问题提供了新的思路和方法，但传统的数据压缩处理方法仅能依赖于奈奎斯特采样频率来实现数据压缩和重构，其算法复杂、耗时，传感节点功耗大，难以在远程医疗应用中推广。本研究针对传感节点硬件和加速度数据非稀疏性特点，提出了一种用于低功耗的加速度数据压缩感知框架，旨在尝试探寻在传感节点低功耗基础上准确压缩和重构加速度数据。如何寻找压缩算法复杂性低且有助于改善重构算法性能和传感节点硬件简化设计的测量矩阵，是本研究的关键所在。

从理论上讲，选取或设计测量矩阵对于实现压缩感知框架中的压缩、重构算法至关重要。在研究中，为满足体域网加速度数据特点和传感节点硬件简化设计需求，尝试基于优化设计稀疏二进制测量矩阵，构建体域网加速度数据压缩感知框架，旨在充分利用稀疏二进制测量矩阵元素0和元素1，简化压缩感知算法的复杂性，有效降低传感节点功耗，优化数据重构性能。从图2、3的实验结果来看，当优化稀疏二进制测量矩阵中每列元素1个数为6、压缩率为40%时，能够获得与高斯随机测量矩阵和伯努利随机测量矩阵几乎相同的压缩重构性能，这可能是由于获取最优d值的稀疏二进制测量矩阵，在一定压缩率的情况下，能够获得与高斯随机测量矩阵和伯努利随机测量矩阵相同的稀疏度[11]。此外，本研究还评估了稀疏二进制测量矩阵d值变化对加速度压缩数据重构性能的影响。从图4、5的实验结果来看，在相同压缩率状况下，稀疏二进制测量矩阵d值变化对加速度压缩数据重构性能的影响稍小。但就每个所选取稀疏二进制测量矩阵d值而言，加速度压缩数据重构性能随着压缩率的增大而降低，在实际优化选取稀疏二进制测量矩阵每列元素1个数时，应考虑压缩率对压缩数据重构性能的影响，需在数据压缩率与其重构性能之间折衷选取[7,9,10,13]。这些结果表明，通过优化稀疏二进制测量矩阵，不仅能有效改善加速度数据压缩、重构性能，而且可充分利用优化稀疏二进制测量矩阵仅含少量元素1个数的特点，明显减少传感节点计算开销，有助于将传感节点硬件集成于片上系统(on-chip)，有利于其计算资源(如寄存器、内存)合理配置，无需配置复杂存储器，使传感节点体积小、功耗低、易于舒适穿戴，便于在远程医疗环境下推广和应用。

此外，基于优化稀疏二进制测量矩阵能否准确重构加速度数据，也是研究中探讨的关键问题。考虑到加速度数据非稀疏性，本研究中尝试将加速度数据基于块结构划分，采用块稀疏贝叶斯学习算法，探寻加速度数据块内在稀疏性，提高非稀疏加速度数据重构性能。从表1的实验结果来看，笔者所提加速度数据重构算法性能明显优于传统压缩感知重构算法性能，表明块稀疏贝叶斯学习算法能够充分利用加速度数据块结构内在相关性，捕获加速度数据块内在块稀疏性，有效提高重构算法性能。但是，研究所提重构算法的重构时间稍高于一些传统压缩感知重构算法的重构时间，这可能是由于传统压缩感知重构算法充分利用加速度数据已知先验知识，求解迭代时间消耗小；而块稀疏贝叶斯学习算法主要利用加速度数据未知先验知识，尝试利用少量投影压缩数据，以高概率重构原始加速度数据，将消耗更多的求解迭代时间。在实际应用中，可将算法复杂的非稀疏加速度数据重构算法置于远程数据处理系统高性能计算机上运行，其重构时间可在一个可接受的处理范围内[6-8]。

4 结论

本研究提出了一种用于低功耗的体域网加速度数据压缩感知框架，通过优化设计稀疏二进制测量矩阵，有效压缩加速度数据，显著降低传感节点传输数据量和功耗，同时也可有效改善非稀疏加速度数据重构性能，为进一步构建低功耗体域网人体活动远程监测系统提供新的思路和途径。下一步的工作主要基于本研究成果，优化设计体域网传感节点、路由节点硬件系统，搭建可行的低功耗体域网人体活动远程监测系统，为远程人体运动治疗、康复评价提供有效平台。

[1]HadjidjA,SouilM,BouabdallahA,etal. Wireless sensor networks for rehabilitation applications: challenges and opportunities [J]. Journal of Network and Computer Applications, 2013, 36(1): 1-15.

[2] 石欣, 张涛. 一种可穿戴式跌倒检测装置设计 [J]. 仪器仪表学报, 2012, 33(3): 576-580.

[3] Balouchestani M, Raahemifar K, Krishnan S. Compressed sensing in wireless sensor networks: survey [J]. Canadian Journal on Multimedia and Wireless Networks, 2011, 2(1): 231-239.

[4] 王天荆, 张宝玉, 杨震. 基于滤波的压缩感知信号采集方案 [J]. 仪器仪表学报, 2013, 34(3): 573-580.

[5] Anumbhuti K, Manish S, Vijay BN. ECG data compression using dwt [J]. International Journal of Engineering and Advanced Technology, 2011, 1(1): 11-13.

[6] Fauvel S, Ward R. An energy efficient compressed sensing framework for the compression of electroencephalogram signals [J]. Sensors, 2014, 14(1): 1474-1496.

[7] Mamaghanian H, Khaled N, Atienza D,etal. Compressed sensing for real-time energy-efficient ECG compression on wireless body sensor nodes[J]. IEEE Transactions on Biomedical Engineering, 2011, 58(9): 2456-2466.

[8] Dixon AMR, Allstot EG, Gangopadhyay D,etal. Compressed sensing system considerations for ECG and EMG wireless biosensors [J]. IEEE Transactions on Biomedical Circuits and Systems, 2012, 6(2): 156-166.

[9] Zhang Z, Jung T, Makeig S,etal. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse Bayesian learning [J]. IEEE Transactions on Biomedical Engineering, 2013, 60(2): 300-309.

[10] Zhang Z, Jung T, Makeig S,etal. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware [J]. IEEE Transactions on Biomedical Engineering, 2013, 60(1): 221-224.

[11] Donoho D. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[12] Donoho D. For most large underdetermined systems of linear equations, the minimal l1-norm solution is also the sparsest solution [J]. Communications on Pure and Applied Mathematics, 2006, 59(6): 797-829.

[13] Gilbert A, Indyk P. Sparse recovery using sparse matrices [J]. Proceedings of the IEEE, 2010, 98(6): 937-947.

[14] Zhang Z, Rao B. Extension of SBL algorithms for the sensing framework of block sparse signals with intra-block correlation [J]. IEEE Transactions on Signal Processing, 2013, 61(8): 2009-2015.

[15] Tropp J, Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.

[16] Berg E, Friedlande M. Probing the pareto frontier for basis pursuit solutions [J]. SIAM Journal on Scientific Computing, 2008, 31(2): 890-912.

[17] Mohimani H, Massoud B, Jutten C. A fast approach for overcomplete sparse decomposition based on smoothed l0 norm [J]. IEEE Transactions on Signal Processing, 2009, 57(1): 289-301.

[18] Zou H, Hastie T. Regularization and variable selection via the elastic net [J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2005, 67(2): 301-320.

[19] Eldar Y, Kuppinger P, Bolcskei H. Block-sparse signals: uncertainty relations and efficient recovery [J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3042-3054.

[20] Yu L, Sun H, Barbot J,etal. Bayesian compressive sensing for cluster structured sparse signals [J]. IEEE Transactions on Signal Processing, 2012, 92(1): 259-269.

[21] Huang J, Zhang T, Metaxas D. Learning with structured sparsity [J]. The Journal of Machine Learning Research, 2011, 12(2): 3371-3412.

[22] Zhang M, Sawchuk A. USC-HAD: a daily activity dataset for ubiquitous activity recognition using wearable sensors [C] // Anind KD, eds. Proceedings of the 2012 ACM Conference on Ubiquitous Computing. Pittsburgh: ACM, 2012: 1036-1043.

A Novel Application of Compressed Sensing for the Accelerometer Data from Wireless Body Area Network with Low Energy Consumption

Wu Jianning1*Xu Haidong1Wang Jue2

1(SchoolofMathematicsandComputerScienceofFujianNormalUniversity,Fuzhou350007,China)2(KeyLaboratoryofBiomedicalInformationEngineeringofEducationMinistry,Xi’anJiaotongUniversity,Xi’an710049,China)

This paper proposed a novel scheme of energy-efficient compressed sensing framework for processing the acceleration-based data acquired from wireless body area networks (WBANs), in order to save the energy of WBANs-based system. With the optimal scheme of sparse binary matrices, the raw accelerometer data with non-sparse is compressed by linearly projected at sensor node before their transmission, and then the compressed data is reconstructed by the novel block Bayesian learning algorithm (BSBL) at remote terminal. The acceleration data from USC-HAD dataset of Southern California was used to evaluate the effectiveness of our proposed technique. The experimental results showed that the optimal scheme of sparse binary matrix could obtain the same reconstruction error (0.0045) as Gaussian or Bernouilli random matrix when a number of nonzero values were selected as 6 in each column of the designed sparse binary matrix and the ratio of compression was 50%. Besides, compared with the traditional CS-based reconstruction algorithms, our proposed BSBL algorithm for reconstruction of acceleration data could increase by 17 dB of signal-noise ratio, significantly improving the performance of reconstruction of acceleration data. These results suggested that, with the optimal design of sparse binary matrix, the designed compressed sensing framework could acquired the acceleration data at sub-Nyquist sampling rate and greatly reduce the number of transmitted data by simple linear transform at sensor node for saving energy. It also can contribute to improving the performance of reconstruction of non-sparse acceleration data by using BSBL. Our work can provide a novel approach for further practical implementation such as the design of simple hardware of sensor node, improvement of the performance of reconstruction of acceleration-data and the development of WBANs-based system with lower energy consumption for remote monitoring physical activity.

compressed sensing; low energy consumption; acceleration-based data; wireless body area networks; telemedicine

10.3969/j.issn.0258-8021. 2015. 06.006

2015-02-10， 录用日期:2015-08-30

国家科技支撑项目(2012BAI33B01)；福建省自然科学基金(2013J01220)；福建省高等学校教学改革研究专项(JAS14674)

TN98; TP391

A

0258-8021(2015) 06-0677-09

*通信作者(Corresponding author)， E-mail: jianningwu@fjnu.edu.cn