独立同分布环境中上临界配对依人口数两性分支过程

常克亮，陈贵景

(山西大同大学 数学与计算机科学学院,山西 大同 037009)



独立同分布环境中上临界配对依人口数两性分支过程

常克亮，陈贵景

(山西大同大学 数学与计算机科学学院,山西 大同 037009)

[摘要]本文考虑的是独立同分布随机环境上临界配对依人口数两性分枝过程，得到了该过程的灭绝概率的渐近上、下界.

[关键词]两性分枝过程；随机环境；依人口数；灭绝概率.

两性分枝过程作为一种比较有代表性的两类型分枝模型是由Daley 首先提出的，后来人们又提出了变化环境中的两性分枝过程，带移民的两性分枝过程及随机环境中的两性分枝过程模型[1-6].本文考虑的是独立同分布随机环境上临界配对依人口数两性分枝过程，得出了该过程的灭绝概率的渐近上、下界.

该模型定义如下：

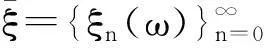
Z0=N,

Zn+1=LZn(Fn+1,Mn+1).

(1)

模型的主要结论及证明

假设

E(-log(1-gξn(0)))<+∞；

其中ⅰ)是{Zn}为上临界(即对∀N≥1,有qN<1)的充分条件

定理1假设存在一个α1>0，使得Q(α1)=1且Q′(α1)<+∞，则存在一个常数c1>0,

Xn+1=ηξn(ηξn-1(…(ηξ0(0)…))

现令Y:=-log(1-X)，Yn:=-log(1-Xn)，则：

Yn+1=-log(1-Xn+1)

=Yn+vn.

注意到Yn≥0，故Yn+1≥max{0,Yn+vn}.

对∀n≥0，令W0=0,Wn+1=max{0,Wn+vn}

P{Y

现令1-e-y=x，有y=-log(1-x),x∈[0,1],则

P{X

现再令：u0=-log(1-s0)，

其中s0∈[0,1]，具体取值待定.

定理2若s0充分接近于1，且存在一个α2=α2(s0)>0，使得R(α2)=1和R′(α2)<+∞，则存在一个常数c2=c2(s0)>0，使得

对∀x∈[0,1]成立.

证明的剩余部分，可取s0充分接近1时对应的α2=α2(s0)及Y′，U，X′代替定.

定理3在定理1和定理2的条件下，存在常数0<α1，α2<+∞，且0

证明：由定理1和定理2易得.

结论：最终得到了独立同分布环境配对依人口数两性分枝过程的灭绝概率的渐近上、下界.

[参考文献]

[1]Smith WL, Wilkinson WE. On branching processes in random environments [J].Acta.Math.Appl.Sinica.,2006,22:1-10.

[2]Athreya K B, Karlin S. On branching processes with random environments[J]. Ann.Math.Stat.1971, 42: 1499-1520.

[3]Wang, H.-X. Extinction of population -size-dependent branching processes in random environments[J].J.Appl.Prob.,1999,36: 146-154.

[4]Wang Han-Xing,Da Fan-Fang.Asymptotic behavior of population-size- dependent branching processes in Markovian random environments[J].J.Appl.Prob. Trust., 1999, 20:611-619.

[5]By David Tanny. Limit theorems for branching processes in a random environment[J].The Annals of Probability.1977,Vol.5,No.1,100-116.

[6]卢准炜. 随机环境中的分枝过程[J]. 应用概率统计，1998,14(3).

[责任编辑：Z]

[中图分类号]0212.7

[文献标识码]A

[文章编号]1671-5330(2015)02-0008-02

[作者简介]常克亮，男，河北唐山人，主要从事概率与数理统计方向的研究与教学。

[收稿日期]2015-01-28