基于有色噪声自适应卡尔曼滤波的GPS单点定位
2015-02-19夏志浩赵长胜马晓君
夏志浩,赵长胜,马晓君
(1. 金坛市城乡测绘院,江苏 金坛 213200; 2. 江苏师范大学城建与环境学部,江苏 徐州 221116)
GPS Single Point Positioning Based on Adaptive Kalman Filter of the Colored Noise
XIA Zhihao,ZHAO Changsheng,MA Xiaojun
基于有色噪声自适应卡尔曼滤波的GPS单点定位
夏志浩1,赵长胜2,马晓君2
(1. 金坛市城乡测绘院,江苏 金坛 213200; 2. 江苏师范大学城建与环境学部,江苏 徐州 221116)
GPS Single Point Positioning Based on Adaptive Kalman Filter of the Colored Noise
XIA Zhihao,ZHAO Changsheng,MA Xiaojun
摘要:将有色噪声一阶AR模型的自适应卡尔曼滤波应用到精密单点定位中,采用当前历元的预测残差均方根误差与上一历元的观测残差均方根误差的比值确定相关系数ρspan。在使用一阶AR模型进行解算时,使用实测数据对模型进行验证,证明了该方法确定的相关系数能够有效提高扩展卡尔曼滤波(EKF)解算过程中的收敛速度和幅度。
关键词:扩展卡尔曼滤波;AR模型;自适应;有色噪声
一、引言
有色噪声可以看成一个平稳的时间序列,通常使用自回归(AR)模型,滑动(MA)模型和自回归滑动平均(ARMA)模型等方法进行建模[1]。在使用AR模型进行建模时,由于相关系数ρk,k-1在整个数据解算的过程中是一个时变参数,而不是一个固定量,因此相关系数难以确定。滤波估计参数向量的初始协方差阵和动态噪声向量协方差矩阵的确定也是一个难点,而合理的初值和协方差矩阵才能保证动态定位的准确性。
本文在使用一阶AR模型进行解算时,采用当前历元的预测残差均方根误差与上一历元的观测残差均方根误差的比值来确定相关系数,有效地避免了相关系数的取值不当,提高了扩展卡尔曼滤波解算过程中的收敛速度和幅度。
二、一阶AR模型自适应滤波
对观测值的噪声使用一阶AR模型对有色噪声进行建模[2]
u(tk)=ρk,k-1u(tk-1)+ξk
(1)
式中,ρk,k-1为k-1与k历元的相关系数矩阵;u(tk-1)为k-1历元的观测噪声中的非高斯部分;ξk为高斯白噪声向量。将式(1)代入扩展卡尔曼滤波的状态方程和观测方程可得
(2)
(3)

则状态方程和观测方程为
(4)
(5)
三、滤波初值的选取
滤波初值的选取直接影响滤波的收敛速度和滤波的是否发散,因此选择合适的初值对动态精密单点定位有很大的影响。
GPS单点定位参数的初值为
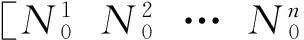
使用以下初始方差矩阵可获得较好的效果。
状态估计向量的初始协方差矩阵为
式中,τ为观测数据的采样间隔;n为每个历元的卫星数。
观测向量的协方差矩阵为
动态噪声向量协方差矩阵为
四、算例分析
以上海站2012-01-04T14∶19∶00—2012-01-04T16∶31∶30的静态观测数据为例,采样间隔为30s,分别使用扩展卡尔曼滤波(EKF)和基于一阶AR模型的扩展卡尔曼滤波(AKF&AR)进行计算,结果如图1—图3所示。

图1 X轴坐标差值比较

图2 Y轴坐标差值比较

图3 Z轴坐标差值比较
从图中可以看出,基于一阶AR模型的扩展卡尔曼滤波(EKF&AR)比扩展卡尔曼滤波(EKF)的收敛速度和幅度都得到了提高。两种滤波最后都近似收敛于同一曲线,这是由于一开始是将IGS参考站已知坐标作为起算初始值,相对应的系统噪声向量协方差取0.000 3,系统噪声向量协方差较小,增大预测值对结果的影响,使得最终坐标都收敛于该点。由此可以看出,卡尔曼滤波在进行解算的过程中无论是白噪声还是有色噪声都能起到去噪作用(见表1)。
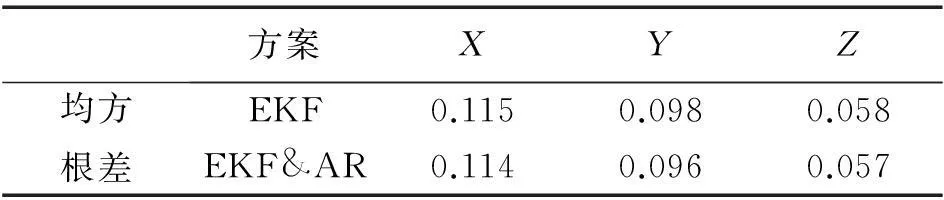
表1 EKF和AKF&AR两种算法误差对比图 m
由表1可以看出,本文中的改进方法可以使3个方向收敛后的均方根差分别减少1 mm、2 mm和1 mm,在滤波解算的过程中,定位结果更加接近坐标的真实值。
如图4所示,ρk,k-1分别取0.3、0.5、0.8和当前历元的预测残差均方根误差与上一历元的观测残差均方根误差的比值r。从图中可以看出当取0.5和0.8时,观测噪声中的非高斯部分u(tk)随着时间推移有增大的趋势;当取0.3和r时,u(tk)相对比较平稳,更加符合AR模型是基于平稳的时间序列的假设。

图4 ρk,k-1取值对u(tk)的影响
由表2中可以看到,分别为扩展卡尔曼滤波及其与AR模型组合的无电离层载波相位观测值残差ξk的均方根误差。ξk为高斯白噪声向量,无论ρk,k-1取0.3还是r都要比EKF的残差均方根误差小,而使用本文方法确定的ρk,k-1更加接近于0,满足白噪声的假设。
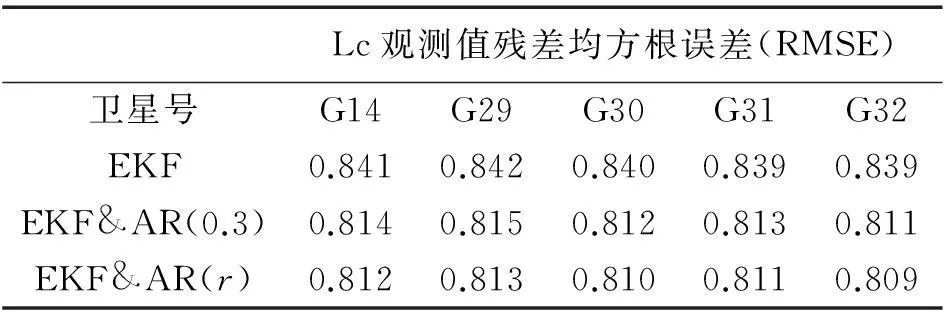
表2 EKF和AKF&AR Lc观测值残差均方根误差 m
五、结论
1) 从坐标差值分析,本文中基于一阶AR模型的扩展卡尔曼滤波能够有效地减少观测值之间的有色噪声,平滑卡尔曼滤波定位曲线,提高定位的精度。
2) 未知相关系数ρk,k-1采用当前历元的预测残差均方根误差与上一历元的观测残差均方根误差的比值确定,能够反映ρk,k-1为时变参数的性质,更加符合一阶AR模型的假设。
3) 观测值的相关性与采样间隔有关,本文采用的是30 s间隔的静态观测数据,有色噪声相对较小,因此EKF和EKF&AR的定位误差曲线会逐渐重合。
参考文献:
[1]曹轶之.非高斯/非线性滤波算法研究及其在GPS动态定位中的应用[D].郑州:信息工程大学,2012.
[2]崔先强.动态定位有色噪声自适应抗差滤波理论的拓展与应用研究[D].西安:长安大学,2012.
[3]崔先强,杨元喜,高为广.多种有色噪声自适应滤波算法的比较[J].武汉大学学报:信息科学版,2006,31(8):731-735.
[4]赵长胜,陶本藻.有色噪声作用下的抗差卡尔曼滤波[J].武汉大学学报:信息科学版,2007,32(10):880-882.
[5]赵长胜,陶本藻.有色噪声作用下的卡尔曼滤波[J].武汉大学学报:信息科学版,2008,33(2):180-182,207.
[6]杨元喜,崔先强.动态定位有色噪声影响函数——以一阶AR模型为例[J].测绘学报,2003,32(1):6-10.
[7]崔先强.动态导航有色噪声的影响与控制[D].郑州:信息工程大学,2002.
[8]崔先强,樊月波.有色噪声模型参数改进算法[J].测绘学院学报,2002,19(3):174-177,181.
引文格式: 夏志浩,赵长胜,马晓君. 基于有色噪声自适应卡尔曼滤波的GPS单点定位[J].测绘通报,2015(3):66-68.DOI:10.13474/j.cnki.11-2246.2015.0077
作者简介:夏志浩(1988—),男,硕士生,主要研究方向为GNSS数据处理理论及应用。E-mail:cehuixzh@sina.com
基金项目:国家自然科学基金(41174032)
收稿日期:2014-02-17
中图分类号:P228.4
文献标识码:B
文章编号:0494-0911(2015)03-0066-03
