GNSS星座模拟器关键问题研究

王孟阳，应忍冬，刘佩林，赵　毅

(1. 上海交通大学，上海 200240； 2. 上海华测导航技术有限公司， 上海 200233)

Research on Key Problems of GNSS Constellation Simulator

WANG Mengyang,YING Rendong,LIU Peilin,ZHAO Yi



GNSS星座模拟器关键问题研究

王孟阳1，应忍冬1，刘佩林1，赵毅2

(1. 上海交通大学，上海 200240； 2. 上海华测导航技术有限公司， 上海 200233)

Research on Key Problems of GNSS Constellation Simulator

WANG Mengyang,YING Rendong,LIU Peilin,ZHAO Yi

摘要：引入轨道力学模型，采用一种轨道外推的解析方法，简单有效地实现了卫星轨道根数及卫星位置的推算。根据星历误差来源，提出并实现了一种基于星历参数拟合的广播星历误差模拟方案。经验证，该方案可以用于产生径向、切向和法向误差可配置的广播星历，更灵活、更真实地模拟广播星历误差。

关键词：全球导航卫星系统；星座；星历误差；外推；拟合

一、引言

全球导航卫星系统(global navigation satellite system, GNSS)信号模拟器是卫星导航终端设备的开发、测试及性能评估的重要工具，在系统仿真试验中起到了关键的作用[1]。信号模拟器要根据用户配置的环境场景，对信号发射、传播和接收的整个过程进行仿真，对各项误差和干扰进行模拟，最后生成载体接收的卫星信号。而星座模拟器是信号模拟中的重要模块，主要用于模拟整个星座中各颗卫星的运动情况，并生成卫星播发星历。

在星座模拟器中，模拟卫星运动通常有两种实现方法：①从RINEX或其他格式的星历文件中读取卫星轨道参数，据此计算卫星的位置和速度，同时将其作为播发电文中的星历参数；②先获取卫星的初始状态(由轨道参数或卫星的初始位置、速度来定义)，而后应用卫星轨道外推算法，计算仿真时段内的卫星轨迹。比较两种实现方式，第一种实现简单，但是仿真时间受到星历参考时间的限制，场景配置不够灵活；第二种方法则没有这方面的限制，但是需要应用轨道力学理论，对卫星运动过程所受到的各项作用力、摄动作用建模，实现难度较大，而且这种方法往往需要应用星历参数拟合算法，从星历参考时间前后的卫星位置坐标中拟合出一套播发星历。现实中，卫星的播发星历参数是在预测的卫星天线相位中心坐标的基础上，采用最小二乘法拟合出来的。因而，从播发星历的生成过程上来看，第二种实现方案更接近真实情况。本文中的星座模拟器，正是采用这种方案。

二、轨道外推

轨道外推是指由卫星的初始状态推算另一时刻卫星状态的过程。轨道外推算法可以模拟卫星在任意时刻的运动过程，而不必受限于可用的星历数据文件。然而，通常的轨道外推算法需要对卫星在空间受到的作用力与摄动进行建模，利用数值积分方法求解，需要较深的轨道力学理论基础，实现起来也较为复杂。

文献[2—3]提出了一种实现简单的轨道外推算法，其利用解析公式对轨道根数进行外推，可以由一套卫星初始轨道根数推算得到任意时刻的卫星轨道根数。算法基于地球非球形引力的J2摄动项模型，考虑了J2摄动的一阶影响，对平均轨道根数进行外推：轨道半长轴a、偏心率e和轨道倾角i不受影响，轨道升交点赤经Ω、近地点角距ω及平近点角M随时间发生变化

(1)

(2)

(3)

(4)

由式(2)—式(4)可以看出，给定初始轨道根数，等式右边将是不变量，即Ω、ω及M将随时间呈线性变化。由此，得到全部的外推公式

(5)

(6)

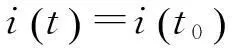
(7)

(8)

(9)

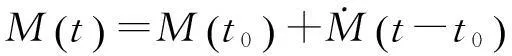
(10)

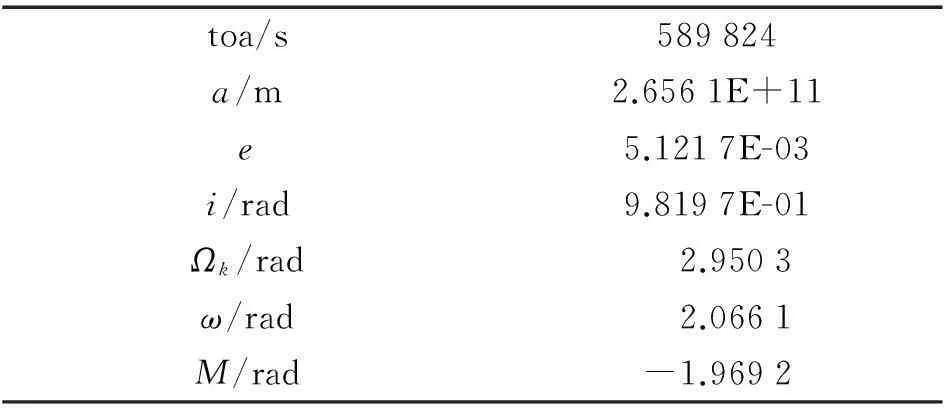
通过从GPS播发的历书文件中可以提取历书参考时间下的轨道根数，以此作为卫星的初始轨道根数，可以外推出一段时间后的卫星位置。图1所示为从历书参考时间开始，对GPS第13号卫星进行外推得到的卫星三维坐标(WGS-84坐标系下)。历书参数来自于GPS已播发的电文，参考历元是GPS时间第708个星期(星期计数始于1999年8月22日)。各项轨道参数的数值见表1。从图1中可以看出，外推的卫星坐标曲线平滑，且符合GPS卫星的运行周期规律：X和Y坐标曲线的周期近似为24 h，Z坐标的周期约为12 h。

图1　外推得到的卫星三维坐标

toa/s589824a/m2.6561E+11e5.1217E-03i/rad9.8197E-01Ωk/rad 2.9503ω/rad 2.0661M/rad-1.9692

三、星历误差模拟

GNSS的广播星历是由空间段或地面控制段对卫星轨道进行预测后采用最小二乘等方法拟合出的一套参数。由轨道预测上的偏差所引起的卫星星历误差，是GNSS接收机的系统误差之一，影响着接收机定位解算结果的精度。

星历误差可在3个方向上投影：卫星运动的径向、切向和法向。一些文献通过对比广播星历与精密星历的计算结果，对广播星历的各分量误差进行了统计和分析[4-5]。根据文献[5]，GPS在投入运行以来，广播星历的精度一直在改进，到2006年，径向、切向和法向的日均方根误差分别达到0.6 m、1.5 m、0.9 m左右。

将星历误差在卫星-用户视线方向上投影，可换算成等效测距误差，它是星历偏差引发定位误差的主要原因。一些GNSS信号模拟器正是通过测距误差来间接地模拟卫星星历误差的[6-8]。也有模拟器在设计时则忽视了对星历误差的建模[9]，其他一些文献则没有对星历误差处理方法予以说明[7,10]。本文将从广播星历产生的过程出发，提出一种星历误差的模拟方法。

星历误差既然是通过对预测的(不精确)卫星坐标而产生的，那么，模拟器可以通过在星历拟合点处，人为地在卫星的“准确”坐标上加入误差量，再进行星历参数拟合，从而获得含有误差的广播星历。可以预期，通过控制加在各点在径向、切向和法向上的误差量，能够拟合出符合不同偏差分布的星历参数。

关于星历拟合算法，很多文献中都有提及。本文中的拟合算法，主要参考了文献[11]中第3、4部分。采用最小二乘拟合算法，利用差分法求解卫星坐标对各星历参数的偏导数；拟合初值的获取，可以由外推至星历参考时间toe的轨道根数直接转化而来。为了验证拟合算法的有效性，采用算例1进行测试。

1. 算例1

为验证拟合算法的有效性，将前一次外推的卫星坐标作为卫星的准确位置，选取星历参考时间toe=597 600 s，对toe前后两小时的卫星坐标进行拟合(采样间隔为300 s)，再利用拟合出的星历重新计算卫星坐标，与准确值对比，统计三维距离误差为0.065 8 m，拟合曲线如图2所示，可见拟合精度基本控制在0.1 m之内，拟合误差较小。

图2　星历拟合算法的三维误差

为验证星历误差模拟方案的有效性，设计算例2进行试验。

2. 算例2

在算例1中选取的所有拟合点上加入0.6 m的径向偏差、1.5 m的切向偏差，以及0.9 m的法向偏差，然后进行星历参数拟合。用拟合出的星历重新计算星历参考时间toe前后两小时内的卫星坐标，统计三维均方差和径向、切向和法向的误差。拟合结果如图3所示，拟合的三维均方根误差为1.847 5 m，径向平均误差为0.595 6 m，切向平均误差为1.498 1 m，法向平均误差为0.900 0 m，与设定的误差指标相吻合。

图3　引入星历误差后的拟合结果

算例2的试验结果表明，通过在各拟合点上引入径向、切向和法向上的误差，能够让拟合出的广播星历误差在3个方向上的偏差满足设定的指标。

四、结束语

本文针对GNSS卫星星座模拟器的两项关键功能提出了实现方案。首先，根据轨道力学公式，引入了卫星轨道根数的外推算法，有相关文献证明算法在较长时间的外推后，不会改变星座分布规律；基于此，本文提出了外推公式的另一种应用方法，利用外推的轨道根数来求解卫星的位置，而不是用于直接外推出播发星历。经验证，推算法求出的卫星轨迹曲线平滑，且在周期性变化规律上与实际卫星的运行情况相吻合。

另外，本文提出了一种星历误差的模拟方法。传统方法是将星历误差换算成等效的测距误差，是出于对星历误差的作用效果的考虑；而本文提出的方案，是出于对星历误差的实际来源的考虑而提出的。结合星历参数拟合算法，本文所采用的星历误差模拟方案，可以实现径向、切向和法向上星历偏差的多元化配置，且与实际场景更加相符。星历误差模拟算法配合轨道外推算法，使得星座模拟器的场景和参数配置更加灵活，模型仿真更接近真实情况。

致谢：本工作受到了上海市北斗导航与位置服务重点实验室和上海华测导航技术有限公司的资助，在此表示感谢。

参考文献：

[1]张硕, 寇艳红. GNSS 模拟器中频调制卡设计与实现[J]. 北京航空航天大学学报, 2009, 35(5): 555-558.

[2]张伯川, 常青, 张其善, 等. 高动态 GPS 卫星信号模拟器导航电文生成[J]. 北京航空航天大学学报, 2005, 31(3): 284-287.

[3]SENGUPTA P. Satellite Relative Motion Propagation and Control in the Presence of J2 Perturbations[D]. Texas：Texas A&M University, 2003.

[4]李征航, 丁文武, 李昭. GPS 广播星历的轨道误差分析[J]. 大地测量与地球动力学, 2008, 28(1): 50-54.

[5]WARREN D L M, RAQUET J F. Broadcast vs Precise GPS Ephemerides: a Historical Perspective[J]. GPS Solutions, 2003, 7(3): 151-156.

[6]DONG L, MA C, LACHAPELLE G. Implementation and Verification of a Software-based IF GPS Signal Simulator[C]∥National Technical Meeting.[S.l.]： ION，2004: 26-28.

[7]JULIEN O, ZHENG B, DONG L, et al. A Complete Software-based IF GNSS Signal Generator for Software Receiver Development[C]∥ION GNSS 17th International Technical Meeting of the Satellite Division.Long Beach：[S.l.]，2004: 2146-2157.

[8]WANG Y, ZHAO M, ZHONG J, et al. Design and Implementation of Programmable Multi-mode GNSS Signal Simulator[C]∥2010 12th IEEE International Conference on Communication Technology (ICCT).[S.l.]：IEEE, 2010: 865-868.

[9]YIN X, KOU Y, ZHANG Z. Design and Implementation of a Flexible Software-based GNSS IF Signal Simulator[C]∥Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2009).[S.l.]：ION，2001: 2229-2240.

[10]WON J H, KO S J, LEE J S. Design and Test Results of Software Based if Level GPS Signal Simulator[C]∥Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2004).[S.l.]：ION，2001: 305-315.

[11]陈刘成, 韩春好, 陈金平. 广播星历参数拟合算法研究[J]. 测绘科学, 2007, 32(3): 12-14.

引文格式： 王孟阳，应忍冬，刘佩林,等. GNSS星座模拟器关键问题研究[J].测绘通报，2015(3)：19-21.DOI:10.13474/j.cnki.11-2246.2015.0066

作者简介：王孟阳(1989—)，男，硕士生，研究方向为GNSS接收机及模拟器技术。E-mail:myw1313@gmail.com

基金项目：国家科技部863项目(2012AA12A209)；上海市科委科研计划项目(13511501200)

收稿日期：2014-02-25

中图分类号：P228.4

文献标识码：B

文章编号：0494-0911(2015)03-0019-03