一种新型激光测距定位系统交会角适用条件研究

张　超，李得海，章传银，秘金钟，宋志英

(1. 中国地震局第一监测中心，天津 300180； 2. 中国测绘科学研究院，北京 100830；

3. 山东科技大学，山东 青岛 266510； 4. 河北政法职业学院建设工程系，河北 石家庄 050061)

Study on Application Condition of Different Interaction Angle of

a New Laser Ranging Positioning System

ZHANG Chao，LI Dehai，ZHANG Chuanyin，BEI Jinzhong，SONG Zhiying



一种新型激光测距定位系统交会角适用条件研究

张超1,2,3，李得海2，章传银2，秘金钟2，宋志英4

(1. 中国地震局第一监测中心，天津 300180； 2. 中国测绘科学研究院，北京 100830；

3. 山东科技大学，山东 青岛 266510； 4. 河北政法职业学院建设工程系，河北 石家庄 050061)

Study on Application Condition of Different Interaction Angle of

a New Laser Ranging Positioning System

ZHANG Chao，LI Dehai，ZHANG Chuanyin，BEI Jinzhong，SONG Zhiying

摘要：介绍了一种与全球定位系统相结合的新型激光测距定位系统，从其基本原理出发，构建了其数据处理过程中相关平差模型及随机模型。首先从理论研究两测站不同平面交会角对系统平面定位精度的影响，然后组合试验中各测站的数据得出，平面交会角小于10°与大于165°时平面定位精度低，为系统不适用条件；交会角从10°~30°与150°~165°为困难条件；30°~150°为系统最佳条件。

关键词：测距定位；全球导航定位系统；最小二乘；测量平差

一、引言

本文介绍的新型激光测距定位系统，是由全球定位系统(GPS)、激光测距仪、罗盘等系统组合形成的新系统，即GPS激光测距定位系统[1]。该系统打破了全站仪只能在静态已知站进行测距定位的工作方式，能够在动态载体上获取目标点的三维坐标；同时解决了远距离、无棱镜和无控制网情况下的目标定位需求。虽然国内外一些机构对GPS与激光测距仪集成作过研究，但是这些系统对载体平台及仪器精度要求很高，而且造价相对昂贵[2-3]。相比较，该系统的要求则较低，但对数学模型及观测条件有一定的要求。本文对该系统的数据处理方法进行研究，结合试验验证理论推导的测量条件的正确性。

二、系统原理与数据处理方法

GPS激光测距定位系统主要由GPS定位、激光测距、三维数字罗盘、供电系统、掌上电脑、数据控制中心(实时质量控制模块、数据存储模块及目标粗略定位模块)等模块构成[4]。其基本原理如图1所示。

测站(Si)的坐标通过中国测绘科学研究院开发的Rover软件计算获取，仪器的姿态信息(测站到目标的方位角以及测站仪器的俯仰角)由系统的电子罗盘测量获取，测站到目标点的距离由系统的激光测距子系统测量获取。

图1　GPS激光测距定位系统基本原理

假设目标点的坐标为T(X,Y,Z)，每一测站的坐标为Si(xi,yi,zi)。根据空间前方交会原理即可求得目标点的三维坐标

(1)

式中，(x，y，z)为差分后计算的测站三维坐标；d为激光测距仪所测距离；β、α为罗盘所测的俯仰角与方位角；(X，Y，Z)为目标点坐标。

从式(1)可以看出，仅观测一站即可得到目标点的坐标。但是这样会造成测量误差不可探测，导致测量结果不可靠。为得到准确的目标点坐标必须进行多次观测，通过多余观测量来提高定位精度，即求解多点距离和姿态来确定目标点坐标。

根据上述基本原理，建立平差模型与随机模型，如下：

1. 函数模型

方位角误差方程为

(2)

高度角误差方程为

(3)

距离误差方程为

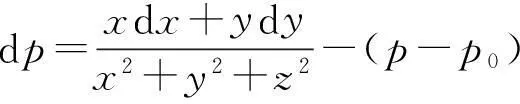
(4)

式(2)—式(4)中，x为横坐标；dx为横坐标改正数；y为纵坐标；dy为纵坐标改正数；ΔAz为方位角系统误差；Az为方位角观测值；Az0为方位角计算值；dAz为方位角改正数；z为竖直方向坐标；dz为改正数；ΔEl为高度角系统误差；El为高度角观测值；El0为高度角计算值；dEl为高度角改正数；p为距离观测值；p0为距离计算值；dp为距离改正数。

2. 随机模型

距离观测配权为

PL=L2/(a+bL)2

(5)

角度测量配权为

PL=1802/(επ)2

(6)

式中，a为测距离标定的加常数，单位为m；b为测距仪标定的乘常数，无量纲；ε为罗盘的测角标称精度，单位为(°)。

在测站坐标系(NEU)内，建立姿态、距离误差方程。将测站坐标转换为地心地固系(ECEF)，以目标点的ECEF位置改正数和罗盘高度角及方位角的系统误差为待估参数，再对观测方程线性化，组建法方程。利用最小二乘算法，迭代估计得到目标点坐标。但若最小二乘解不收敛，就无法求出目标点的坐标，这时可利用线性迭代的方法[5-7]来求解。

两站n次距离测量与目标定位平面精度的关系[8]为

(7)

两站n次方向交会精度评估公式为

(8)

可简单地对距离和方位交会角结果进行加权分析。若考虑距离因素分别以(1，1/s)为距离和方位交会结果配权,其中，两站n次距离和方位测量与目标定位平面精度的关系为

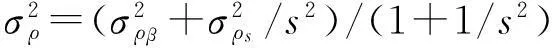
(9)

按照上述理论，假设4次重复交会目标点，做交会目标点平面精度随交会角2°~180°的变化图，如图2所示。

图2　距离方向4次交会目标点平面精度随交会角2°～180°的变化

由图2可以看出，平面定位精度与传统前方交会定位变化规律相吻合[9-10]。交会角小于10°的目标点，定位外符合误差达到10m，但结算结果仍向目标点收敛。交会角大于165°的两站观测目标，定位外符合误差也达到10m。结算误差偏大的原因为观测图形结构图形较差，导致估计结果明显大大受到观测噪声的扰动影响。

三、试验与结果分析

按照上述交会目标点定位平面精度变化的理论计算结果，以及该系统设计原理，针对不同交会角对该系统定位精度的影响程度，将试验场地选在临岸的海域，目标点架设在岸上不易被周围物体遮挡的地方，其三维坐标是利用网络RTK技术进行解算得到的，解算精度在厘米级[11-12]，满足试验要求。测站架设在航行的船上，并保证测量时测站间的交会角在0°～180°之间。在数据处理时，总体分为小于10°、10°～165°、大于165°三大类试验。

为了减弱因个别仪器自身的系统误差对定位精度的影响，采用了6台仪器进行测量试验，每台仪器同测站都处于相邻的区域，并且进行多次测量。

首先选取其中一台(编号006)的观测数据，其平面定位中误差见表1。

表1　006号仪器随交会角变化其平面定位中误差变化

从表1可以看出，角度小于10°与大于165°的平面定位中误差较在10°～165°之间的平面定位中误差大，说明定位内符合误差在10°～165°时较小，验证了理论分析的正确性。

再利用6台仪器的全部观测数据，在上述交会角条件下，定位精度统计见表2。

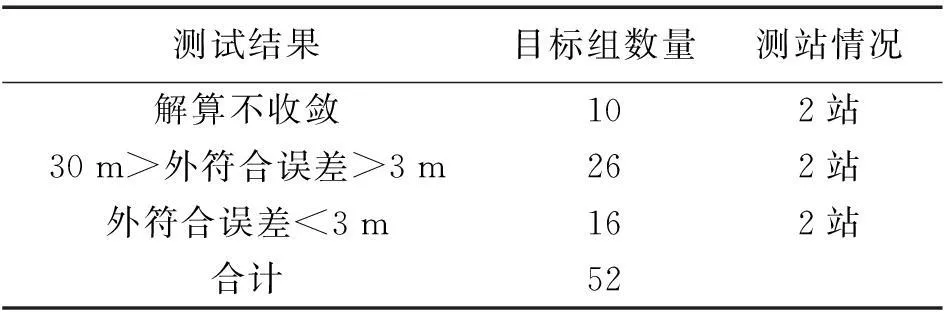
表2　观测数据在小于10°和大于165°时定位精度统计

统计表显示，在交会角小于10°和大于165°的情况下，由于图形结构差，目标初值计算受噪声影响较大，会造成迭代不收敛的情况，而且即使收敛，目标定位精度较差的情况在所有目标组数量中所占比例也很大。

对上述观测条件下的目标定位结果，求其相对于已知参考位置在N、E、U方向的偏差dN、dE、dU，得到目标定位的外符合误差分布离散情况，如图3所示。

图3　小交会角6台仪器(两站)目标定位外符合误差随交会角变化图

图3显示交会角小于10°的目标点，定位外符合误差大10 m，但结算结果仍向目标点收敛。交会角大于165°的两站观测目标点，定位外符合误差高达30 m，而且有20%的目标点解算结果不收敛。

交会角适用条件下定位数据选取为：交会角在10°～165°之间两测站观测数据。两测站条件下，目标定位的外符合误差随交会角变化情况如图4所示。

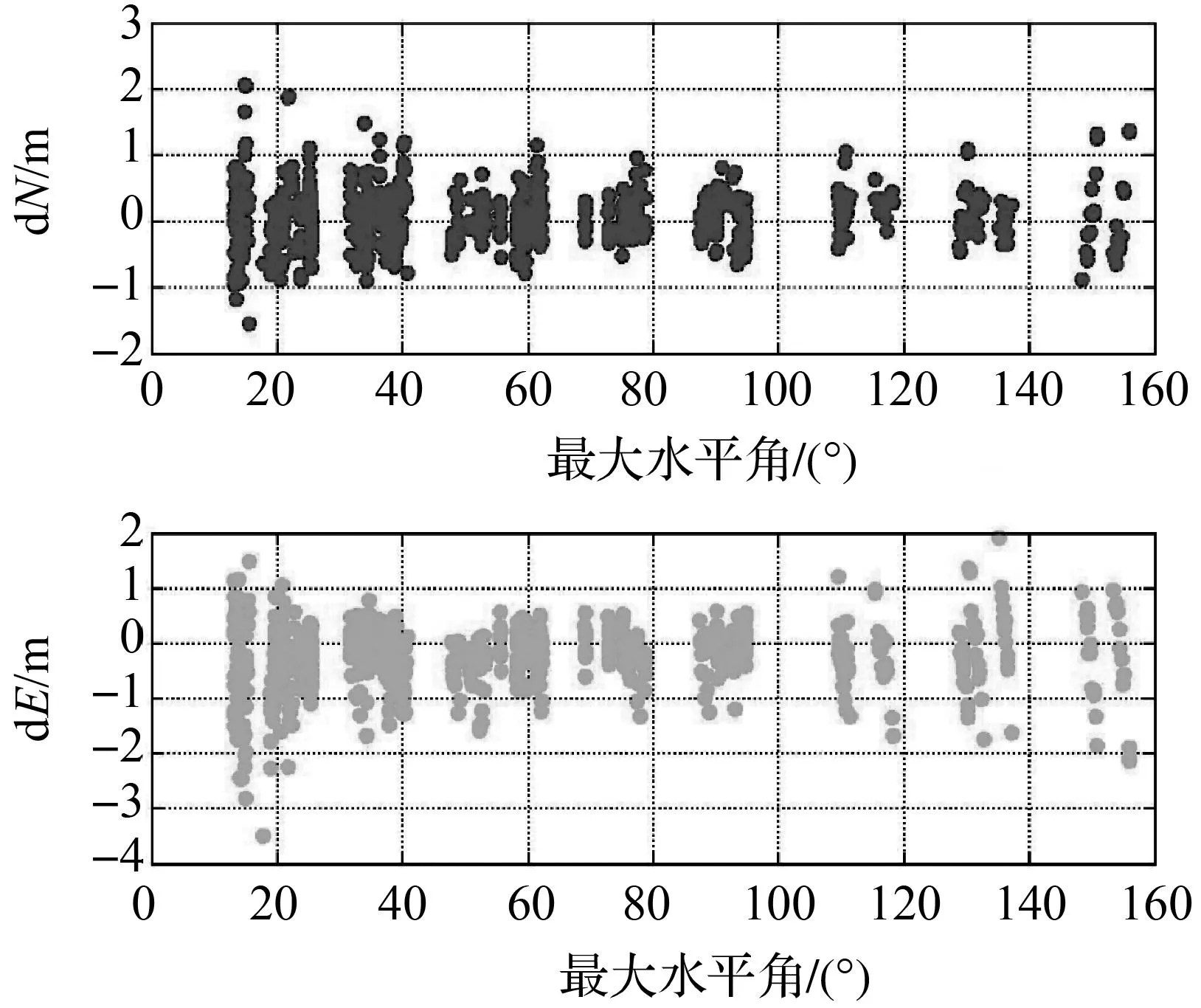
图4　交会角适用条件下6台设备(两站)目标定位外符合误差随交会角变化图

图4显示交会角为10°~165°的目标点，解算结果收敛正确，但10°~30°与150°~165°交会角范围内，定位精度较低。主要原因是30°~150°观测图形结构好，解算误差偏差小。

四、结束语

从上述试验结果可以得出，交会角小于10°或大于165°的观测条件为该系统不适用条件；交会角在10°~30°和150°~165°为系统困难但适用的条件；交会角在30°~150°为系统最佳适用条件。本文仅对不同交会角对该系统定位精度的影响进行了评估，选出了该系统的适用的最佳交会角范围，但观测距离和测站数目对定位精度的影响还有待研究。

参考文献：

[1]陈品馨. GPS激光测距定位系统关键技术研究与实现[D].北京：中国测绘科学研究院，2010.

[2]卢秀山，李清泉，冯文灏，等.车载式城市信息采集与三维建模系统[J].武汉大学学报：工学版,2003，36(3):76-80.

[3]邹晓亮.车载测量系统数据处理相关技术研究[D].郑州：信息工程大学，2011.

[4]谭瑞. GPS激光测距定位系统在无法到达区的研究[J].测绘科学，2013，38(2):135-136.

[5]黄昆学. GPS激光测距系统的算法研究及实现[D].青岛：山东科技大学，2010.

[6]李庆杨，王能超，易大义，等. 数值分析[M].武汉：华中科技大学出版社，2008.

[7]同济大学应用数学系. 线性代数[M].北京：高等教育出版社，2008.

[8]隋立芬，宋立杰. 误差理论与测量平差基础[M].北京：解放军出版社，2004.

[9]武汉大学测绘学院. 测量学[M].北京：测绘出版社,1980.

[10]张永军，张勇. 大重叠度影像的相对定向与前方交会精度分析[J].武汉大学学报：信息科学版，2005，30(2):126-130.

[11]HU G R, KHOO H S, GOH P C,et al. Development and Assessment of GPS Virtual Reference Stations for RTK Positioning[J].Journal of Geodesy,2003，77(5-6): 292-302.

[12]LANDAU H,VOKKATH U,CHEN X M.Virtual Reference Station Systems[J].Journal of Global Positioning Systems,2003,1(2):137-143.

引文格式： 张超，李得海，章传银,等. 一种新型激光测距定位系统交会角适用条件研究[J].测绘通报，2015(3)：16-18.DOI:10.13474/j.cnki.11-2246.2015.0065

作者简介：张超(1987—)，男，硕士生，研究方向为GNSS导航定位及数据处理。E-mail:zhangchao.87@hotmail.com

基金项目：科技部863重点项目(2011AA120503)；科技部科技支撑计划(2012BAB16B01)；科技部863计划(2013AA122501)；国家青年科学基金项目(41304030)

收稿日期：2014-01-23

中图分类号：P228.4

文献标识码：B

文章编号：0494-0911(2015)03-0016-03