拉曼激光相位噪声对原子干涉重力仪测量分辨力的影响

2015-02-17季俊云王宇

计测技术 2015年6期

关键词：锁相环

季俊云，王宇

(中航工业北京长城计量测试技术研究所计量与校准技术国防科技重点实验室，北京100095)

拉曼激光相位噪声对原子干涉重力仪测量分辨力的影响

季俊云，王宇

(中航工业北京长城计量测试技术研究所计量与校准技术国防科技重点实验室，北京100095)

摘要：原子干涉重力仪已获得当今g值测量的最高分辨力，使得其在前沿科学研究和精密计量中有广阔的应用前景，但其分辨力的提高受限于包括拉曼激光相位噪声在内的各种噪声。本文通过对拉曼激光相位噪声模型和原子干涉仪中噪声传递过程的研究，发现微波信号源贡献了拉曼激光相位噪声的主要部分；通过计算常见T，τ条件下拉曼激光相位噪声对干涉仪重力测量分辨力的影响，发现100～300 ms内T越大重力仪测量分辨力越高，其中在T=300 ms、τ=20 μs的条件下，单次测量时拉曼激光相位噪声对原子干涉仪相位波动的影响为19.6 mrad，相应对重力仪分辨力的影响为1.35 μGal(1 μGal=10-8m/s2)。

关键词：相位噪声；拉曼激光；原子干涉仪；锁相环

0引言

1991年Stanford大学的S.Chu小组利用冷原子喷泉和受激拉曼跃迁技术首次实现了原子干涉仪，其对于惯性力高度敏感，可用于测量加速度和转速，相应地可制成重力仪和陀螺仪。经过多年的发展，原子干涉重力仪的测量分辨力显著提高，性能已超过以FG-5为代表的传统重力仪，成为重力精密测量的有力工具，进一步拓展了其在导航定位、矿物勘探、引力波探测、广义相对论验证、引力常数测定等领域的应用。

原子干涉重力仪工作过程如下：真空腔中的三维磁光阱俘获并囚禁原子团，将其速度分布对应的温度降至μK量级；改变磁光阱参数使原子团上抛形成原子喷泉；上抛过程中，一系列微波与激光脉冲将原子团制备在磁不敏感的能态(F=1，mF=0)上，并选出速度分布与后续拉曼脉冲匹配的原子；在上抛顶点处，三对脉宽分别为τ，2τ和τ的反向拉曼脉冲依次与原子团作用，使得原子团在两个能态之间分束、反转与合束并发生干涉，该过程中需扫描拉曼激光的频率差以补偿重力导致的原子感受激光频率的多普勒频移，与拉曼耦合有关的光学相位印在了原子质心波函数中；拉曼脉冲结束后，探测脉冲与原子团作用并探测荧光大小，以此推算出不同能态原子布居概率；布居概率的波动反映干涉相位的变化，通过对干涉条纹进行处理可得重力加速度值[1-3]。

由原子干涉仪的结构及其实现过程可知，限制原子干涉仪测量分辨力提高的因素种类繁杂，如环境振动噪声、拉曼光相位噪声、原子散粒噪声及探测噪声、拉曼光光强噪声、拉曼光波前相差以及磁场导致的噪声等。其中振动噪声和拉曼光相位噪声为主要噪声源，对上述噪声的研究可指导重力仪测量精度的提高。

2012年，华中科技大学胡忠坤组设计的主动隔振系统的自然共振频率降低至0.016 Hz，可将0.1~1 Hz内竖直方向的振动噪声衰减40 dB，该系统用于其获得4.2 μGal/Hz1/2(100 s)重力测量短期灵敏度的实验[4-5]。2007年，法国LNE的F.Pereira Dos Santos等人研究了拉曼光传输延迟对重力测量灵敏度的影响，得出干涉仪相位抖动正比于反射路径长度(对应传输延迟)，3 ns传输延迟导致的激光频率噪声对干涉仪相位的影响为2.4 mrad(单次测量)[6]；2011年，该组研究发现原子横向运动导致的科里奥利加速度和拉曼光波前畸变对原子干涉重力仪测量不确定度的影响分别为0.4 μGal和4 μGal[7]。2014年，意大利LENS的G.M.Tino小组基于对冷却光强度抖动、探测光频率及强度抖动、拉曼光强度抖动和磁场抖动等对干涉仪噪声影响的研究，改进重力梯度仪并获得了3 μGal/Hz1/2(1 s)的差分重力测量短期灵敏度，进一步提高受限于仪器的量子投影噪声极限，他们还通过8000 s连续测量获得了0.05 μGal的差分重力加速度测量分辨力[8]。2015年，Stanford大学的M.A.Kasevich小组研制的70 cm基线长度的水平重力梯度仪获得4.2 μGal/Hz1/2的差分重力测量灵敏度，相应每台重力仪的测量灵敏度为3 μGal/Hz1/2，他们将其用于测定引力常数和验证牛顿平方反比定律[9]。

本文仅就拉曼光相位噪声角度，结合现有拉曼光产生方式，系统讨论其对于原子干涉重力仪测量分辨力的影响，并对原子干涉重力仪的研制给出建议。

1拉曼光噪声传递

1.1　拉曼激光相位与重力加速度

采用三能级的碱金属原子Rb作为敏感原子，调节双光子失谐Δ远大于|i〉态自然线宽Γ，能有效抑制自发辐射，从而等效为二能级原子体系，实现|a〉态到|b〉态的跃迁(图1)，δ12为拉曼光频差相对于共振频率的单光子失谐。

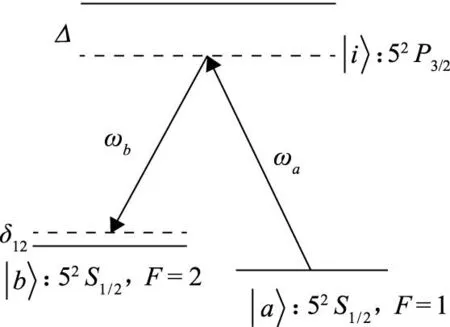
图1　Rb原子三能级体系

(1)

式中：M为演化矩阵；t0为作用初始时刻；t为作用后任意时刻；ΩR为拉比频率；φ为拉曼激光的相位差。脉宽τ=t-t0，故M也可表示成t0和τ的函数。假设拉曼光严格共振(δ12=0)且通过调节两束激光光强比为(ωab+Δ)/(ωab-Δ)以补偿交流斯塔克频移，则可得演化矩阵[1，10]。

M(t0，τ，Ωeff，φ)=

(2)

原子自由演化阶段，Ωeff=0，演化矩阵成为

(3)

类似可得自由演化阶段|a〉态和|b〉态分布概率不变。

图2　拉曼跃迁型原子干涉仪

原子干涉实验中，τ的大小需要根据实验测得的拉比振荡频率来确定，根据别的小组现有实验结果，本文首先取τ=20μs，T=100ms进行分析，对于反向拉曼脉冲，|keff|=|k1-k2|=1.61×107/m，此时有干涉仪相位ΔΦ=1.6×106rad，若需重力测量分辨力Δg/g达到10-9量级，相应要求干涉仪相位抖动在mrad量级。

1.2　拉曼激光相位噪声的传递

考虑拉曼激光相位抖动对重力测量的影响，假设拉曼光相位发生δφ的跳变，导致跃迁概率变化δP(δφ，t)，定义灵敏度函数：

(4)

式中：Φ为干涉仪相位；φ为拉曼激光相位。当Φ=π/2时，干涉仪对相位抖动最敏感，通常干涉仪工作在该位置，故

(5)

对(2)，(3)式描述的过程，可得灵敏度函数[12]为

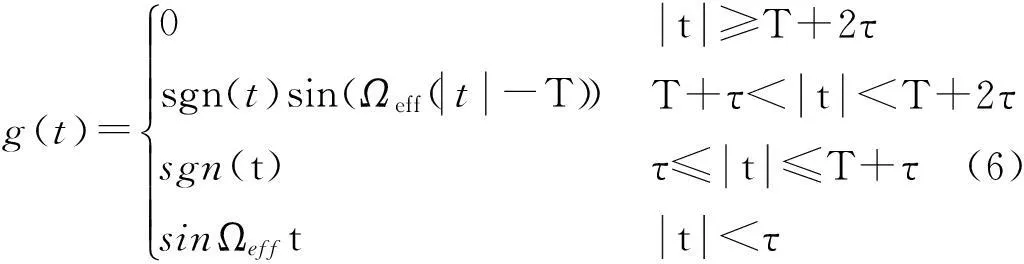
引入拉曼光相位正弦调制φ(t)=A0cos(ω0t+ψ)，则有干涉仪相位抖动：

(7)

式中：G(ω)为g(t)的傅里叶变换。对于随机分布的调制相位ψ，有δΦ的均方根值为

(8)

(9)

式中：SΦ(ω)为拉曼光相位噪声的功率谱密度。对于拉曼脉冲Ωeffτ=π/2，令ω=2πf，根据g(t)的傅里叶变换公式和超越函数积分可得

(10)

对于T=100 ms，τ=20 μs的情形，|H(2πf)|2图像如图3所示。

(a) 宽频双对数图

(b) 低频单对数图

图3拉曼光相位噪声传递函数(T=100 ms，τ=20 μs)

由(10)式可知，特定频率(f=k/(T+2τ))的拉曼光相位噪声并不影响干涉仪的相位，由图3知|H(2πf)|2的包络具有带通性质，低频截止频率∝1/T，高频截止频率∝1/τ，通带以外频率的噪声对干涉仪的影响可忽略，设计光锁相环时确保锁相带宽大于该高频截止频率。式(10)描述单次测量时拉曼光噪声的传递函数，对于多次连续重力测量，不妨设进行m次时长为Tc的单次测量，则噪声传递函数[10]变为

(11)

2拉曼光噪声模型

两束相位差恒定的拉曼激光通常由光锁相环实现，两束激光拍频探测，激光的频差与相位差转化为电信号的频率和相位，采用锁相环将该信号的频率与相位锁定至低相噪的参考信号源上，从而实现拉曼激光的锁定。图4为光锁相环简化框图，图5为其噪声传递模型，各器件噪声作为加性噪声[13]引入。其中ML(Master Laser)和SL(Slave Laser)分别为主、从激光器，主激光器事先经饱和吸收谱稳频(SAS，Saturated Absorption Spectroscopy)锁定至原子跃迁线对应的频率上；DDS(Direct Digital Synthesizer)为直接数字频率合成器，也即信号源；PD(Photoelectric Detector)为光电探测器；mixer为混频器；PFD(Phase Frequency Detector)为鉴频鉴相器；LC(Loop Controler)为环路控制器；Kd，F(s)，K0/s为PFD，LC和SL的传递函数。从mixer到Raman光输出为前向通路，从Raman光输出到mixer为反馈通路。

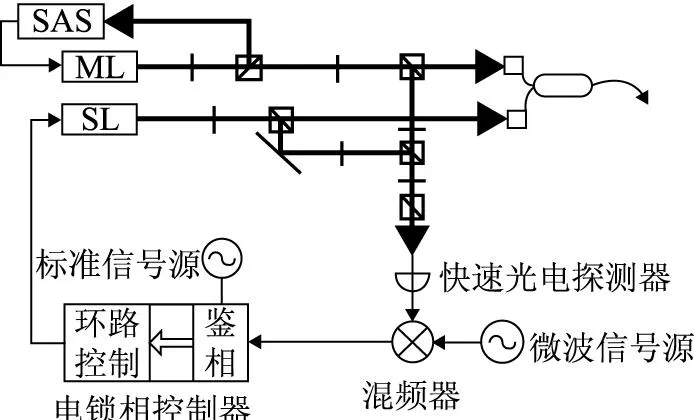
图4　光锁相环构成

图5　光锁相环噪声传递模型

该模型的噪声传递满足：

(12)

可得拉曼激光相位噪声为

(13)

式中：φRaman表示拉曼光相噪；φDDS，φPD，φmixer，φPFD，φLC，φbeat分别表示DDS信号源、光电探测器、混频器、鉴频鉴相器、环路控制器和拍频引入的相噪。H(s)=KdK0F(s)/[s+KdK0F(s)]为锁相环闭环传递函数，锁相环的直流增益KdK0通常需要设计得足够大，对于以半导体激光器作为压控振荡器的光锁相环，直流增益可达109量级，故可认为在锁相环带宽内|H(s)|=1，在其带宽外|H(s)|=0，故拉曼光拍频噪声不计入拉曼光相位噪声。根据功率谱密度的定义，由(13)式可知拉曼光相噪的功率谱密度为

(14)

相位噪声谱通常由随机相位噪声的连续谱与周期性相位噪声的离散谱组成，其形式一般可表示为[13，16]

(15)

式中：f为噪声频率相对载波的频偏；h0项为白噪声；h1/f项为闪烁噪声；h2/f2项为白噪声调制；h3/f3项为闪烁噪声调制；h4/f4项为随机游走噪声调制。在双对数坐标图中其为各分项的分段函数相连，根据不同器件可能会有缺省。

根据文献[17]归纳的锁相环各器件的噪声特性，可知在0.1~1 MHz频段内，ECL型鉴相器的噪声功率谱：SPFD=10-11/f；混频器的噪声功率谱：Smixer=10-14/f+10-17；环路控制器的噪声功率谱可忽略不计；根据文献[18]光电二极管的噪声模型和G4176-03数据手册，可得光电探测器的噪声功率谱：SPD=10-11.5/f。

DDS1采用E8257D，DDS2采用33250A，两者内部都采用了10 MHz时基晶振，晶振的噪声模型为[17]

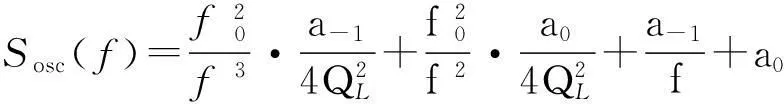
(16)

式中：f0为晶振频率；QL为晶振固有损耗。直接数字频率合成器DDS通过对高稳晶振进行数字分频得到任意频率，该过程中噪声传递满足[19]：

(17)

式中：fc为DDS输出载波频率。因此DDS的噪声模型与(16)式有同样形式，结合E8257D/UNX手册中的绝对SSB噪声谱可大致得到其载波为10 GHz的噪声谱表达式，其在6.795 GHz载波下的相噪优于式(18)。

DDS2为标准信号源33250A，其手册中关于相噪的表述为：载波为80 MHz时30 kHz带宽内噪声功率小于-47 dBc，载波为10 MHz时30 kHz带宽内噪声功率小于-65 dBc。对(18)式的相噪谱采用自适应递推牛顿-柯西法积分可得其在1~30 kHz内相噪声功率为-49.5 dBc，因此可以判断33250A在载波为80 MHz时的相噪与(18)式在同量级(1.78倍)，而载波为40 MHz时相噪更优。

实际设计电路时鉴频鉴相器后加放大电路可实现增益Kd2=10，将上述器件噪声谱代入(14)可得拉曼光相噪谱密度SRaman，其各器件噪声谱如图6所示。

图6　拉曼光相位噪声谱其各器件噪声谱

从图6可知，DDS信号源贡献了拉曼光相位噪声的主要部分。将(10)，(19)式代入(9)式并进行数值积分，调整积分精度直至结果误差可控，结果显示在T=100 ms，τ=20 μs条件下，0.1 Hz~1 MHz积分区间内原子干涉仪相位噪声满足：(σΦrms)2=6.09×10-5rad2，相应有σΦrms=7.8 mrad，拉曼激光相位噪声对单次重力测量分辨力的影响为Δg/g=4.94×10-9，对应Δg=4.84 μGal。

更改实验时的T，τ组合，权函数改变，相噪水平相应发生变化，根据常用T，τ值选取不同T，τ时拉曼激光相位噪声对重力测量分辨力的影响如表1所示。从表1可知，在100 ms到300 ms内T越大，拉曼激光相位噪声对测量分辨力影响越小；τ在10 μs以上增大时，对重力测量分辨力的影响变化不大。在T=300 ms时，拉曼激光相位噪声对单次重力测量分辨力的影响仅为Δg=1.35 μGal。作为比较，在T=150 ms、τ=40 μs时拉曼激光相位噪声对单次重力测量分辨力的影响为Δg=2.98 μGal，这一结果优于S.Chu小组的早期实验结果(T=160 ms，τ=40 μs时拉曼光高频相位噪声对单次重力测量影响为Δg=10.78 μGal[11])。

值得注意的是，E8257D在载波为6.895 GHz的实际相噪水平要要优于本文中所采用的数据(10 GHz)，同时根据(11)式，多次重力测量时噪声传递的权函数变小，因而拉曼光相位噪声对于重力测分辨力的限制有望进一步降低至10-10量级。然而，本文分析光锁相环的噪声模型时，所考虑的器件噪声还不是很完善，比如拍频后的低噪声放大器以及微波频率链中的耦合器、滤波器以及激光器本身的相位噪声没有纳入模型，同时还会受到锁相环固有噪声及光路的影响。

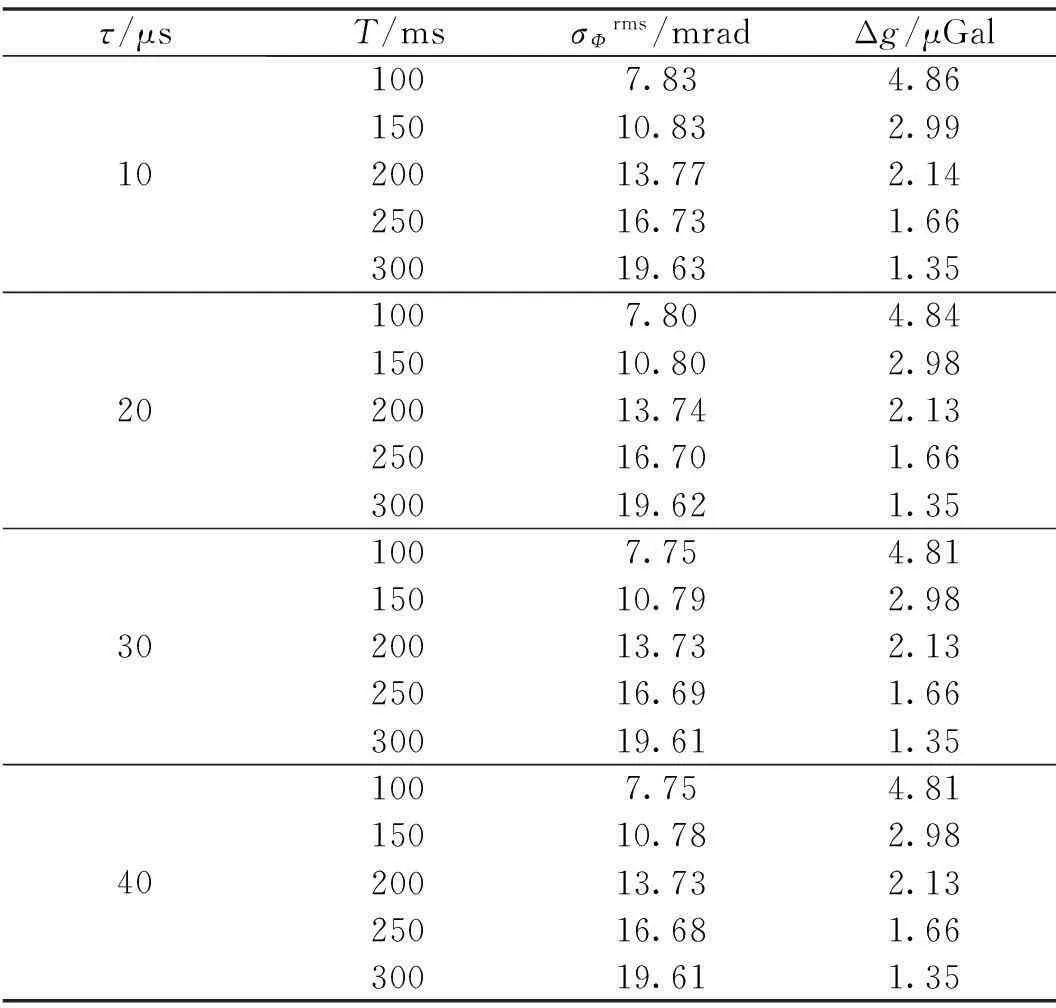
表1　不同T，τ条件下拉曼光相噪对重力测量分辨力的影响

3结论

限制原子干涉仪重力测量分辨力提高的因素很多，其中拉曼光的相位噪声直接影响原子干涉仪的相位抖动。本文仅就拉曼激光相位噪声对原子干涉重力仪测量分辨力影响的角度，系统分析了拉曼激光相位噪声的由来及其对于重力测量噪声的传递，通过计算不同T，τ条件下拉曼激光相位噪声对原子干涉仪相位的影响，得出在100 ms到300 ms范围内增大T可提高重力测量分辨力，而τ在10 μs到40 μs范围内变化对分辨力影响较小。其中在T=300 ms，τ=20 μs条件下，拉曼激光相位噪声对原子干涉仪相位的影响为19.6 mrad，对原子干涉重力仪单次重力测量分辨力的影响为Δg=1.35 μGal。同时通过本文的研究发现进一步突破该限制需要调研或研制更低相噪的DDS，上述这些结果可以指导原子干涉仪的样机研制与精度提高。

参考文献

[1] Torsten Petelski.Atom Interferometers for precision gravity measurements[D].Paris：Université Paris 6，2005.

[2] McGuirk J M，Foster G T，Fixler J B，et al.Se-nsitive Absolute Gravity Gradiometry Using Atom Interferometry[J].Physical Review A，2002，65(3)：033608.

[3] Kathryn Moler，Dacid S Weiss，Mark Kasevich，et al.Theoretical analysis of velocity-selective Raman transitions[J].Physical Review A，1992，45(1)：342-348.

[4] Zhou Minkang，Hu Zhongkun，Duan Xiaochun，et al.Performance of a cold-atom gravimeter with an active vibration isolator[J].Physical Review A，2012，86 (4)：043630.

[5] Hu Zhongkun，Sun Buliang，Duan Xiaochun，et al.Demonstration of an ultrahigh-sensitivity atom-interferometry absolute gravimeter[J].Physical Review A，2013，88 (4)：043610.

[6] Le Gouet J，Cheinet P，Kim J，et al.Influence of lasers propagation delay on the sensitivity of atom interferometers[J].The European Physical Journal D，2007，44(3)：419-425.

[7] Louchet-Chauvet A，Farah T，Bodart Q，et al.The influence of transverse motion within an atomic gravimeter[J].New Journal of Physics，2011，13(6)：065025.

[8] Sorrentino F，Bodart Q，Tino G M，et al.Sensitivity limits of a Raman atom interferometer as a gravity gradiometer[J].Physical Review A，2014，89(2)：023607.

[9] Biedermann G W，Wu X，Kasevich M A，et al.Testing gravity with cold-atom interferometers[J].Physical Review A，2015，91(3)：033629.

[10] Patrick Cheinet，Benjamin Canuel，Franck Pereira Dos Santos，et al.Measurement of the Sensitivity Function in a Time-Domain Atomic Interferometer[J].IEEE Transactions on instrumentation and measurement，2008，57(6)：1141-1148.

[11] Peters A，Chung K Y，Chu S.High-precision gravity measurements using atom interferometry[J].Metrologia，2001，38：5-61.

[12] LE Gouet J，Mehlstaubler T E，Kim J，et al.Limits to the sensitivity of a low noise compact atomic gravimeter[J].Appl.Phys.B，2008，92：133-144.

[13] Floyd M Gardner.锁相环技术[M].3版.姚剑清，译.北京：人民邮电出版社，2007.

[14] 孙步梁.高分辨率原子干涉重力测量实验研究[D].武汉：华中科技大学，2013.

[15] 吴彬.高精度冷原子重力仪噪声与系统误差研究[D].杭州：浙江大学，2014.

[17] Venceslav F Kroupa.Noise properties of PLL systems[J].IEEE Transactions on communications，1982，30(10)：2244-2252.

[18] Enrico Rubiola，Ertan Salik，Nan Yu.Flicker Noise in High-Speed p-i-n Photodiodes[J].Transacactions on Microwave theory and Techniques，2006，54(2)：816-820.

[19] Venceslav F.Kroupa.Close to the carrier noise in DDS[C]//Frequency Control Symposium.50th.Proceedings of the 1996.IEEE International.Piscataway，New Jersey：IEEE，1996：934-941.

Influence of Raman Laser Phase Noise on the Measurement Resolution of Atomic Gravimeter

JI Junyun，WANG Yu

(National Key Laboratory of Science and Technology on Metrology & Calibration，Changcheng

Institute of Metrology & Measurement，Beijing 100095，China)

Abstract：Atom interferometer gravimeter has realized state-of-the-art measurement of ‘g’，thus promising it with broad prospects in frontier scientific research and precision metrology.However，its resolution is limited by different sources of noises，such as Raman phase noise.This paper investigates the Raman phase noise model and its transfer process to the phase of atomic interferometer.We find that signal generator contributes the major part of the Raman phase noise.By calculating the contributions of Raman phase noise to the interferometric phase fluctuation under normal conditions of T & τ，we find that the measurement resolution raises as T increases in the range from 100 ms to 300 ms.For instance，we calculate a contribution of 19.6 mrad/shot to the interferometric phase fluctuation under the condition of T=300 ms & τ=20 μs，corresponding to an influence of 1.35 μGal(1μGal=10-8m/s2)on the resolution of atomic gravimeter in a single measurement circle.

Key words：phase noise；Raman laser；atomic interferometer；phase lock loop

作者简介：季俊云(1991-)，男，硕士研究生，主要从事拉曼激光稳频锁相研究；王宇(1978-)，男，博士，高级工程师，主要从事量子重力计量研究。

基金项目：中国航空工业集团创新基金资助项目(2012F30415R)；中国航空工业集团创新基金资助项目(2014F30443R)

收稿日期：2015-10-20；修回日期：2015-11-02

中图分类号：TB9

文献标识码：A

文章编号：1674-5795(2015)06-0014-06

doi：10.11823/j.issn.1674-5795.2015.06.04