Modelling of*solute transport in a filled fracture: Effects of heterogeneity of filled medium

DOU Zhi （窦智）, ZHOU Zhi-fang （周志芳）

School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, E-mail: Douz@hhu.edu.cn

Modelling of*solute transport in a filled fracture: Effects of heterogeneity of filled medium

DOU Zhi （窦智）, ZHOU Zhi-fang （周志芳）

School of Earth Sciences and Engineering, Hohai University, Nanjing 210098, E-mail: Douz@hhu.edu.cn

(Received June 22, 2013, Revised October 23, 2013)

In this paper, the developed lattice Boltzmann method (LBM) is used to model the solute transport in a filled fracture under a heterogeneous advective velocity field. The results of the developed LBM in modelling the solute transport are compared with the published experimental data. The numerically derived BTCs indicate that the distribution of the filled medium in the fracture has a significant effect on the characteristics of the BTCs, even with the same porosity. The heterogeneity of the filled medium is responsible not only for the heterogeneous advective velocity field but also for the early arrival and long tails of the BTCs. The long tailings of the BTCs increase their length with the increase of the duration of the input pulse. Furthermore, the BTCs obtained from the LBM simulations are well consistent with the two-region model (TRM). The fitting results show that the fractional mobile region varies with the distribution of the filled medium. The long tailings of the BTCs increase their length with the increase of the immobile region while the concentration peak value increases with the increase of the mobile region.

solute transport, heterogeneity, lattice Boltzmann method, two-region model, fracture

Introduction

The conventional solute transport theories in rock fractures were broadly applied in the fields of water resources, groundwater environment and nuclear engineering[1]. Most of these theories are based on the assumption of an ideal fracture structure geometry. The solute transport in a natural fracture is a challenging issue due to the extremely complex fracture geometry[2]. The studies of the solute transport in a heterogeneous filled fracture are few and far between. On one hand, the advective velocity field in the current numerical models is usually assumed to be uniform based on the Darcy’s law that cannot be used to simulate the inertial flow characteristics. On the other hand, a simple advection-dispersion equation (ADE) is not adequate for describing the breakthrough curve (BTC) characteristics in a heterogeneous filled fracture.

A heterogeneous filled single fracture means a single fracture in which a heterogeneous porous medium fills the void spaces. As known in cases of porous media[3,4], the pathway of the solute transport in this heterogeneous filled single fracture strongly depends on the filled medium patterns and it is bounded by fracture wall surfaces. Many classical theories on water flow and solute transport in fractures were investigated by numerical and experimental methods. Huang et al.[5]experimentally studied the effect of branch fractures on the solute arrival time and found that a longer filled branch fracture would lead to a shorter arrival time for the first concentration peak. Qian et al.[6]conducted well-controlled laboratory experiments to investigate solute transport in a single filled fracture under Non-Darcy flow conditions. They found that the water flow was well described by the Forchheimer or the Izbash equations and the Non-Fickian transport was dominated with early arrival and long tailings. A further experimental study was reported by Qian et al.[7]and it was revealed that the resulting BTCs can be better consistently fitted by a tworegion model than the ADE due to the non-uniform advective velocity field. This result indicates that the two-region model is capable of describing the solutetransport for the occurrence of the preferential pathway resulting from the non-uniform advective velocity field. The water flow and the solute transport in the heterogeneous filled fracture are governed by different mechanisms. A careful study of the effect of the heterogeneity on the two-phase flow in porous media was made by Cai and Yu[8]. The heterogeneity of the filled medium may lead to several preferential pathways in the solute transport. Moreover, the characteristics of the preferential pathway strongly depend on the spatial distribution of the heterogeneous filled medium. Thus, different distributions of the heterogeneous filled medium with the same porosity could lead to different preferential pathways and affect the solute transport. Hu et al.[9]investigated the influence of the heterogeneous porosity fields on the flow and solute transport processes. Their results indicate that the spatial variations of the porosity have a significant effect on the pathway of the injected solute plume. Cherblanc et al.[10]reported that there were particularly dual permeability structures composed of high- and low-permeability regions for the solute transport in heterogeneous porous systems. Fiori and Jankovic[11]reported that the heterogeneity had a considerable influence on the emergence of channeling patterns and the preferential pathway. Cai et al.[12]used a full transfixion single fracture to study the solute transport by the continuous injection method and found that the contact area of the filled medium had a significant effect on the BTC characteristics. However, their results are for a regular filled medium.

In order to study the influence of the characteristics of the filled medium on the water flow and the solute transport, the morphological techniques, the X-ray computed tomography, and the micro-tomography were used in many laboratory experiments[13]. However, these methods are difficult to implement, expensive, and time-consuming. Many numerical techniques, such as the self-affinity, the self-similarity, and the random algorithm, were employed to generate a medium with specific prosperities. In this paper, a non-repeated random series is used to generate a filled medium in the fracture with a given porosity.

A large number of numerical models were developed including the properties of the filled medium, and various physical, chemical, and biochemical mechanisms. However, on one hand, the filled medium in these models is assumed to be homogeneous in properties. On the other hand, the advective velocity field is assumed to be uniform or simplified. As a result, the numerical model of the solute transport is still limited in considering both the distribution of the filled medium and the properties of the advective velocity field. In the recent years, the lattice Boltzmann method (LBM), a specific finite difference discretization for the kinetic equation of the discrete velocity distribution function, has attracted a considerable attention due to its simple algorithm and the accuracy. The LBM is a powerful technique for computational modeling of a wide variety of complex fluid flow problems including single and multiphase flows in complex geometries. This method naturally accommodates various boundary conditions such as the periodic condition, the specific concentration and a constant velocity or pressure boundary. Zhang et al.[14]presented a developed LBM for the advection and the dispersion of solute in 3D variably saturated porous media. Zhang et al.[15]used the LBM to solve the ADE and the advection and the anisotropic dispersion equation (AADE). A similar study was reported by Zhou[16]. Anwar and Sukop[17]used the LBM to study the flow and the solute transport in the saturated Karst with consideration of the influence of the matrix rock. Dou and Zhou[18]investigated the influence of fracture roughness on solute transport based on LBM. However, the numerical model based on the LBM has not been used to investigate the flow and the solute transport in a heterogeneous filled fracture with consideration of the nonuniform advective velocity field.

The main objective of this paper is to investigate the solute transport in a heterogeneous filled fracture. Two LB equations are derived to model the water flow and the solute concentration field. The developed LBM is verified by a benchmark numerical case and the results are compared against the published experimental data. Subsequently, the model is applied to investigate the water flow and the solute transport in the heterogeneous filled fracture. Two distributions of the filled medium in the fracture with the same porosity are generated by the non-repeated random series. The resulting flow characteristics, the solute transport patterns, and the BTCs types with different input pulses are discussed and analyzed. Finally, the two-region model (the TRM - a physical non-equilibrium model) is successfully employed to fit the resulting BTCs.

1. Method

1.1 Coupling the flow and the concentration field with LBM

Two distribution functions are used to represent the flow and the concentration field, respectively. The evolution equation of each distribution function satisfies the following lattice Boltzmann equation with a single relaxation time,

where fi(X,t) is the fluid particle distribution function with velocityie at position X and time t, tΔ is the time step, τ is the dimensionless relaxation time, and ci(X,t) is the solute particle distribution function. In the two-dimensional nine-speed (D2Q9) model, the nine possible particle velocities are given by

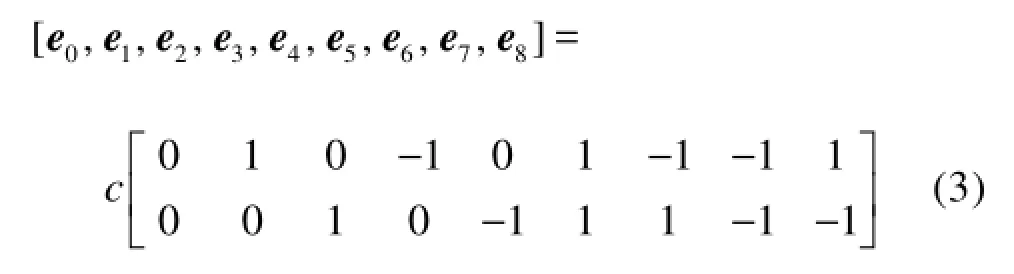
wheresc is the lattice sound speed. the weightssω, for the D2Q9 model, are given by

The macroscopic fluid density, the fluid pressure, and the solute concentration are given by

For different dimensionless relaxation times (τ and τ′) in Eqs.(1) and (2), the corresponding kinematic viscosity and diffusion coefficient are obtained by

Using the Compman-Enskog expansion, the Navier-Stoke equation can be recovered with the second-order accuracy from the lattice Boltzmann model for the fluid field (Eq.(1)). Similarly, the solute particle distribution function (Eq.(2)) can be recovered for the macroscopic ADE. Thus, the governing equations in the model that couples the flow and the concentration field are given by

In our simulations, any lattice node in the computational domain represents either a solid node or a fluid node. All simulations are implemented in ++C code. For the solid node, before the streaming step, a bounce-back algorithm in the collision step is used for the non-slip wall boundary condition in both concentration and advective velocity fields. Although the zero concentration boundary condition could be used for the solid node in the concentration fields, in this work, the bounce-back boundary condition is imposed based on the conservation of mass. For the advective velocity field, the periodic boundary condition is imposed at the inlet and outlet boundaries. In the continuous injection, the constant concentration and the zero concentration are assumed at the inlet and the outlet for the concentration field, respectively. The pulse injection is based on the continuous injection condition. After the continuous injection, the constant concentration boundary at the inlet is turned into the zero concentration boundary for the concentration field, while the boundary conditions for the advective velocity field are kept unchanged.

1.2 Two-region model

In the two-region concept, it is assumed that the water region can be partitioned into mobile (dynamic) and immobile (stagnant) regions. The TRM is based on the ADE with retardation (ADE-R). The solute transport is predominantly advective in the mobile domain but largely diffusive in the immobile domain. The early arrival of the solute is attributed to the preferential flow of the water through larger channels of the wetted pore space. In the mobile region, the solute is transported by an advection-dispersion process,while, in the immobile region, in a rate-limited diffusion process, the solute is exchanged with the mobile region. The 1-D governing equation of the ADE-R with the longitude dispersion coefficientLD is given as

where v is the average velocity and the dimensionless retardation factor R takes a value between zero and one. 1R＜ indicates the retardation during the solute transport. The linear and non-linear chemical reactions between the solute and the solid phase could cause the retardation. Thus, the retardation is considered as a result of the chemical reaction. However, in some cases, the retardation (1)R＜ also indicates that only a fraction of water participates in the solute transport process. The solute transport in the mobile region is mainly achieved through advection, while the water in the immobile region is not a main contributor to the solute transport. It is common to assume that both the hydrodynamic dispersion and advection of solutes cannot be observed in the immobile region. However, there is a solute exchange process between the immobile and mobile water, which is responsible for the physical non-equilibrium transport. Thus, the ADE-R with R＜1 can describe the fact that the occurrence of the immobile or dead region might retard the transport even without the chemical reaction. This retardation is only resulted from a physical non-equilibrium process. The classical analytical solution of Eq.(15) with0C being the injected concentration is given as[6]

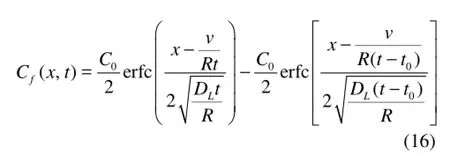
with the following initial and boundary conditions,

The single-region ADE-R is not adequate to describe the physical non-equilibrium solute transport due to the presence of the distinctive immobile or dead region. An alternative to the ADE-R is the tworegion model that assumes the ADE transport in the mobile region and the diffusion-controlled mass transfer between the mobile and immobile regions. The corresponding governing transport equations for the mobile and immobile regions in the absence of the solute adsorption are given as[19]

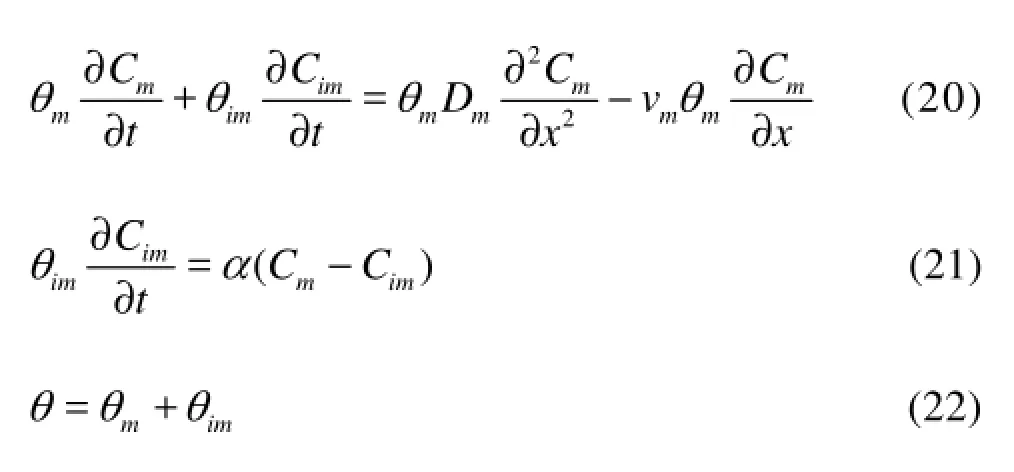
where θ and α are the water content and the mass transfer coefficient, respectively. The subscripts m and im indicate the corresponding variables for the mobile and immobile regions, respectively. The fractional mobile region is defined as β=θm/θ. From above equations, it can be seen that the area of the immobile region has a significant effect on the solute transport. In this work, the STANMOD 2.08 is used for fitting the resulting BTC into the two-region model.

Fig.1 Qualitative comparison of solute transport patterns obtained by the experiment and the simulation. The results from the experiment and the simulation are shown in the upper and down rows, respectively. The gray contour represents the fracture wall and the solute concentration is proportional to the gray scale

2. Results and discussions

2.1 Verification of the developed LBM

In order to verify the developed LBM, the results from a simple case of our simulation are compared against the experiment results reported by Cai et al.[12]. The experiment procedures can be found in the paper of Cai et al.[12]. Due to the limitation of the computerresource, a computational domain of 200×200 lu2representing a fully transfixion single fracture is used for an initial verification test of the developed LBM implementation. Depending on the structure of the fully transfixion single fracture in the experiment, the inlet and the outlet with 10 lu (see Fig.1) are set at the left and right sides of the computational domain, respectively. Initially, the whole fracture is saturated with pure water. Then, the solute is injected continuously by the constant concentration boundary imposed on the inlet. For the outlet, the zero concentration condition is used. For the periodic advective velocity field (with the flow direction from left to right), the Reynolds number is =120Re by adjusting the external body force. Figure 1 shows a qualitative comparison of the solute transport patterns between the current simulation and the previous experiment. It can be seen from Fig.1 that the solute transport patterns from the developed LBM are consistent with the patterns obtained by the experiment. Figure 2 shows a quantitative comparison of the BTCs between the simulation and the experiment. The results from the developed LBM are in a good agreement with those obtained by the experiment. In Fig.2, t is the dimensionless time.

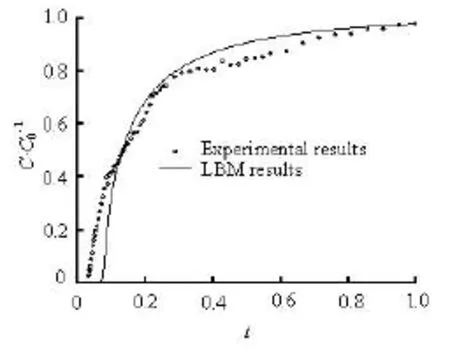
Fig.2 Quantitative comparison of BTCs from the experiment and simulation results

2.2 Distribution of the filled medium

The void space in the filled fracture is represented by a computational domain of 290×290 lu2. The inlet and the outlet with the same size (10 lu) are set at the left and right sides of the void space, respectively. Since the structure of the filled medium is not a concerned topic, the elementary solid node with a computational domain of 10×10 lu2is used to represent the filled medium. It should be noted that the elementary size for solid and void nodes are the same. In order to investigate the effect of heterogeneity of the filled medium on the solute transport, two different distributions of the filled medium in the fractures are generated by the non-repeated random series (see Fig.3). One distribution of the filled medium is regular and another distribution is heterogeneous. It should be noted that the same porosity is used for these two distributions of the filled medium in the fractures. The porosity in the total area of the void space Asis calculated by θ=(As-At)/As=0.76 with Atbeing the total area of the filled medium.

2.3 Flow characteristics

Different distributions of the filled medium in the fracture lead to different flow characteristics. A constant average flow velocity for different distributions of the filled medium in the fracture is achieved by adjusting the external body force. For all simulation cases, the constant average flow velocity takes a value of v =0.002375lu/ts by adding the external body force. It should be noted that the even though the external body force is constant, the resulting average flow velocity is different for different distributions of the filled medium. The water kinematic viscosity is ν=1/3(τ-0.5)=0.067 lu2/ts with τ=0.7. Thus, the Reynolds number for the fracture is =10Re. Here we assume that the advective velocity field is one of laminar flow. The inlet and outlet are at the left and right sides of the fracture, respectively. The periodic boundary condition is imposed on the inlet and outlet. If the average flow velocity difference in 5 000 ts is less than 0.1%, it is assumed that the advective velocity field reaches the final steady-state.

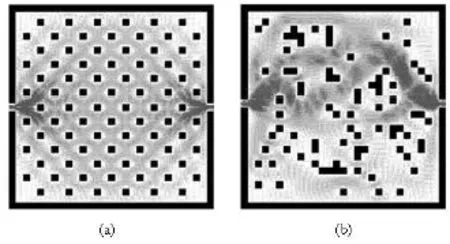
Fig.3 Advective velocity fields for different distributions of the filled medium with the same flow direction (from (a) to (b)). The black block represents the filled medium and the arrow line represents the flow line

Figure 3 shows the advective velocity field for different distributions of the filled medium. It is found that the distribution of the filled medium has a significant effect on the advective field. As expected, the velocity magnitudes near the inlet and outlet are much greater than those in other areas of the fracture. Thus, there are particularly dual-permeability regions in the fracture.

2.4 Solute transport

Several simulations are performed for different distributions of the filled medium. A small diffusion coefficient is used, D=3.3× 10-4lu2/ts . The solutefis injected at the left side of the fracture inlet when the advective velocity field reaches the final steady-state. The durations of the input pulse for the solute are 211 001 ts and 317 001 ts. The corresponding dimensionless pore volumes (PV) are PV=2 and PV=3, respectively. The effluent breakthrough curves are obtained at the outlet and normalized with respect to the inlet concentration.

Fig.4 Solute transport patterns in the heterogeneous filled fracture with the input pulse PV=2. The gray contour represents the filled medium and fracture wall. The black contour represents the pure water. The solute concentration is proportional to the gray scale

Fig.5 Solute transport patterns in the regular filled fracture with the input pulse PV=2

Figures 4 and 5 show the solute transport patterns in the heterogeneous and regular filled fractures with the input pulse PV=2, respectively. From Figs.4 and 5, it can be seen that in general, the pathway of the solute transport is strongly affected by the distribution of the filled medium. The advected and diffused front is non-uniform due to the distributions of the filled medium. With these distributions of the filled medium, two distinctive regions can be seen (the mobile and immobile regions). When the solute is injected at the inlet, the solute is transported preferentially by the advection. On one hand, while the solute is continuiously injected, a preferential pathway of the solute transport is formed. On the other hand, the fronts of the solute plume tend to be indistinct, indicating that the concentration of the fronts decreases. This is because of the variation of the local dispersion. When PV>2, the water begins to flush the fracture. The mobile region allows a quick invasion for the flushing water. However, there is a solute exchange between the immobile and mobile regions. In addition, there are some isolated residual solute regions after a duration of the input pulse. These isolated residual solute regions contribute to the long tailings of the BTCs.

Fig.6 BTCs for different distributions of the filled medium with the input pulse PV=2

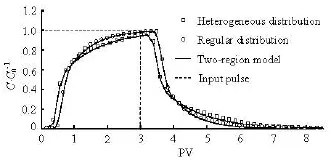
Fig.7 BTCs for different distributions of the filled medium with the input pulse PV=3

Figure 6 shows the BTCs curves for the corresponding results of Figs.4 and 5. These BTCs curves have three distinct features: a sudden rising, a central plateau, and a long tailing. The sudden rising is due to the advective region (the mobile region). Although the average velocity in the fracture is constant in all simulation cases, it can be seen from Fig. 6 that the solute front in the heterogeneous case moves to the outlet of the fracture faster than that in the regular case. This is because different distributions of the filled medium lead to different local advective velocities, even with the same average velocity. There is a stronger preferential pathway due to the fact that the heterogeneity in the heterogeneous case is greater than that in the regular case. The variation of the central plateaus of the BTCs shown in Fig.6 is due to the variation of β. The fraction of the mobile region varies with the distribution of the filled medium, even with the same porosity. However, if the duration of the input pulse becomes infinite, the normalized concentrations at the end of the central plateaus are very close to unity (seeFig.7). When the water begins to flush the fracture, the central plateau of the BTC still has a tendency to rise. The rise in the concentration greatly depends on the amount of the solute in the fracture after the duration of the input pulse. Long tailings can be seen in both heterogeneous and regular cases, as shown in Fig.6. As is known, the long tailing is resulted from the slow solute diffusion from the immobile region. From Figs.6 and 7, it is found that the distribution of the filled medium in the fracture has a significant effect on the rate of the solute diffusion between the immobile and mobile regions. The tailing in the heterogeneous case lasts longer than that in the regular case. In addition, it should be noted that the isolated residual solute regions that contribute to the long tailing of the BTC are observed in the heterogeneous case but not in the regular case.

In order to investigate the effect of the duration of the input pulse on the BTCs, the solute transport with two different durations of the input pulse, PV= 2 and PV=3, is simulated. Figures 6 and 7 show two different features of the BTCs. First, as the duration of the input pulse increases, the area of the central plateaus of the BTCs increases, due to the more injected solute. However, the central plateau in the heterogeneous case is still lower than that in the regular case, which means that the duration of the input pulse has little effect on the fraction of the mobile region. Second, the tailings of the BTCs are very sensitive to the duration of the input pulse. The more solute is injected, the longer a tailing is observed.

The BTCs obtained from LBM simulations are fitted to the two-region model shown as solid lines and the corresponding2R are over 98%. From Figs.6 and 7, it is found that the LBM simulations are very consistently fitted to the two-region model. The fractions of the mobile region obtained from the results of the parameter estimation for the two-region model are =β0.64 and 0.71 in the heterogeneous and regular cases, respectively. This indicates that the distribution of the filled medium is responsible for the variation of the fraction of the mobile region. This variation shows that a single porosity is not adequate to describe the properties of the filled medium in the fracture. Especially, the mobile region in the heterogeneous case is less than that in the regular case, which results in a lower concentration peak in the BTCs in the heterogeneous case. In addition, the long tailings of the BTCs increase with the increase of the immobile region (1)β-.

3. Conclusions

In this work, the developed LBM is used to simulate the solute transport in the heterogeneous filled fracture. Two different distributions of the filled medium are simulated by non-repeated random series. The advective velocity and the concentration fields are coupled by using two distribution functions of the LBM. The capability of the developed LBM in simulating the solute transport in fractures is tested by comparing with the published experimental data. The TRM is applied to explain the characteristics of the BTCs. Three distinct features of the BTCs (a sudden rise, a central plateau, and the long tailing) are captured well by the TRM. The BTCs obtained from LBM simulations are consistently fitted to the TRM.

It is found that the heterogeneity of the filled medium has a significant effect on the distribution of the advective velocity field. The mobile and immobile regions are observed, associated with the occurrence of the preferential pathway. The heterogeneity of the filled medium in fracture enhances the advective velocity of the preferential pathway. As a result, the solute transport in the heterogeneous case is faster than in the regular case. The tailing in the heterogeneous case lasts longer than that in the regular case, which is resulted from the slower solute exchange between the immobile and mobile regions in the heterogeneous case. The isolated residual solute regions after some duration of the input pulse contribute to the long tailings of the BTCs. In addition, the long tailings of the BTCs increase with the duration of the input pulse. However, the duration of the input pulse has little effect on the arrival time of the BTCs.

The two-region analytical model can consistently fit the BTCs. The fitting results show that the fractional mobile region B is different for the heterogeneous and regular distributions of the filled medium in the filled fracture, although with the same porosity. Thus, the fractions of the mobile region vary with the distributions of the filled medium, indicating that a single porosity is not adequate to describe the properties of the filled medium in fracture for the solute transport. Furthermore, the long tailings of the BTCs increase with the increase of the immobile region while the concentration peaks increase with the increase of the mobile region.

Acknowledgements

This study is also supported by China Scholarship Council (CSC) for the first author. We thank Dr. Cai Jin-long for providing his experimental data and photos.

[1] MONDAL P. K., SLEEP B. E. Virus and virus-sized microsphere transport in a dolomite rock fracture[J]. Water Resources Research, 2013, 49(2): 808-824.

[2] CAI J., HU X. and STANDNES D. C. et al. An analy-tical model for spontaneous imbibition in fractal porous media including gravity[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2012, 414(1): 228-233.

[3] CAI J., YU B. and ZOU M. et al. Fractal characterization of spontaneous co-current imbibition in porous media[J]. Energy and Fuels, 2010, 24(3): 1860-1867.

[4] LI Feng-bin, SHENG Jin-chang and ZHAN Mei-li et al. Evolution of limestone fracture permeability under coupled thermal, hydrological, mechanical, and chemical conditions[J]. Journal of Hydrodynamics, 2014, 26(2): 234-241.

[5] HUANG Y., TANG Y. and ZHOU Z. et al. Experimental investigation of contaminant migration in filled fracture[J]. Environmental Earth Sciences, 2013, 71(3): 1205-1211.

[6] QIAN J., CHEN Z. and ZHAN H. et al. Solute transport in a filled single fracture under non-Darcian flow[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 132-140.

[7] QIAN J., ZHAN H. and CHEN Z. et al. Experimental study of solute transport under non-Darcian flow in a single fracture[J]. Journal of Hydrology, 2011, 399(3): 246-254.

[8] CAI J., YU B. A Discussion of the effect of tortuosity on the capillary imbibition in porous media[J]. Transport in Porous Media, 2011, 89(2): 251-263.

[9] HU B., MEERSCHAERT M. M. and BARRASH W. et al. Examining the influence of heterogeneous porosity fields on conservative solute transport[J]. Journal of Contaminant Hydrology, 2009, 108(3): 77-88.

[10] CHERBLANC F., AHMADI A. and QUINTARD M. Two-domain description of solute transport in heterogeneous porous media: Comparison between theoretical predictions and numerical experiments[J]. Advances in Water Resources, 2007, 30(5): 1127-1143.

[11] FIORI A., JANKOVIC I. On preferential flow, channeling and connectivity in heterogeneous porous formations[J]. Mathematical Geoscience, 2012, 44(2): 133-145.

[12] CAI Jin-long, ZHOU Zhi-fang and HUANG Yong. Laboratory experiments on solute transport in a partial transfixion single fracture [J]. Journal of Hydrodynamics, 2011, 23(5): 570-579.

[13] DOU Zhi, ZHOU Zhi-fang and SLEEP B. E. Influence of wettability on interfacial area during immiscible liquid invasion into a 3D self-affine rough fracture: Lattice Boltzmann simulations[J]. Advances in Water Resources, 2013, 61(1): 1-11.

[14] ZHANG X., BENGOUGH A. G. and DEEKS L K. et al. A novel three-dimensional lattice Boltzmann model for solute transport in variably saturated porous media[J]. Water Resources Research, 2002, 38(9): 6-1-6-10.

[15] ZHANG X., BENGOUGH A. G. and CRAWFORD J. W. et al. A lattice BGK model for advection and anisotropic dispersion equation[J]. Advances in Water Resources, 2002, 25(1): 1-8.

[16] ZHOU J. A lattice Boltzmann method for solute transport[J]. International Journal of Numerical Methods in Fluids, 2009, 61(8): 848-863.

[17] ANWAR S., SUKOP M. C. Lattice Boltzmann models for flow and transport in saturated karst[J]. Ground Water, 2009, 47(3): 401-413.

[18] DOU Zhi, ZHOU Zhi-fang. Lattice Boltzmann simulation of solute transport in a single rough fracture[J]. Water Science and Engineering, 2014, 7(3): 277-287(in Chinese).

[19] FEEHLEY C. E., ZHENG C. and MOLZ F. J. A dualdomain mass transfer approach for modeling solute transport in heterogeneous aquifers: Application to the Macrodispersion Experiment (MADE) site[J]. Water Resources Research, 2000, 36(9): 2501-2515.

10.1016/S1001-6058(15)60459-0

* Project supported by the National Natural Science Foundation of China (Grant Nos. 41172204, 51109139), the Natural Science Foundation of Jiangsu Province (Grant No. BK2011110), and the Research Innovation Program for College Graduates of Jiangsu Province (Grant No. CXZZ11_ 0450).

Biography: DOU Zhi (1986-), Male, Ph. D., Lecturer