Flow and heat transfer characteristics around egg-shaped tube*

ZHANG Guan-min （张冠敏）, LENG Xue-li （冷学礼）, ZHOU Nai-xiang （周乃香）, SHI Yan-ping （师艳平）, LI Li-min （李利民）

1. School of Energy and Power Engineering, Shandong University, Jinan 250061, China, E-mail: zhgm@sdu.edu.cn

2. Shandong Urban and Rural Planning and Design Institute, Jinan 250013, China

3. Shanxi Fenxi Heavy Industry Co. Ltd. Technical Center, Taiyuan 030027, China

Flow and heat transfer characteristics around egg-shaped tube*

ZHANG Guan-min （张冠敏）1, LENG Xue-li （冷学礼）1, ZHOU Nai-xiang （周乃香）2, SHI Yan-ping （师艳平）3, LI Li-min （李利民）3

1. School of Energy and Power Engineering, Shandong University, Jinan 250061, China, E-mail: zhgm@sdu.edu.cn

2. Shandong Urban and Rural Planning and Design Institute, Jinan 250013, China

3. Shanxi Fenxi Heavy Industry Co. Ltd. Technical Center, Taiyuan 030027, China

(Received June 22, 2013, Revised January 16, 2014)

This paper studies the flow and heat transfer characteristics around a new type of egg-shaped tubes made up of a semicircle upstream and a semi-ellipse downstream, numerically and experimentally, for Reynolds numbers varying from 4 000 to 5 0000 based on the hydraulic diameter. These tubes have axis ratios, =ε1, 1.5, 2, 3, 4, and 5 with the major axis parallel to the mainstream. When =1ε, the tube is a circular one and when 1/=0ε, it is a flat plate. Numerical results show that the minimum value ofpC occurs at an angular position, which decreases as ε decreases, and the maximum value offC gradually increases with the increase of ε. Simulated results agree very well with those available in the existing literature. The egg-shaped tube has a higher favorable pressure gradient at its front and a lower adverse pressure gradient at its back, that helps the flow delay a separation from the tubes’ surface. Empirical correlations for each tube are obtained by numerical simulations relating the dimensionless heat transfer coefficient with the Reynolds Number and the Prandtl Number. The performance evaluation criterion (PEC) is used to analyze the level of the heat transfer enhancement for egg-shaped tubes. It is found that an egg-shaped tube with =2ε has the best overall heat transfer performance when Re＞11952.

heat transfer enhancement, egg-shaped tube, numerical simulation, flow resistance

Introduction

Circular tubes are widely used in heat exchange equipment because of the ease of production and its capability of withstanding a high pressure. However when the fluid flows across a circular tube, a large separation zone created by the boundary layer separation is developed at the rear of tube, which can result in large pressure drop losses, severe vibrations and even damages to the tube.

In recent years, non-circular tubes with a streamlined outer surface have attracted attentions in the context of saving energies[1-8]. A tube with a cross section of elliptic shape produces less flow resistance and higher heat transfer rates, and comparing with a circular tube, the drag coefficient is reduced by between 10% and 20%[9]. Smooth and fined elliptical tubes have been used widely in a variety of industries (i.e., electric power engineering, metallurgy, oil refining technologies, chemical industry and shipbuilding industry, etc.). The drop-shaped tube is another heat transfer element with high efficiency and energy saving properties. Its cross-sectional profile is shown in Fig.1, which is composed of two sections: circular arc and their tangents. Studies show that the convective heat transfer coefficient increases for the drop-shaped tube by 20%-30% as compared to a circular tube; the drag coefficient is only 30%-50% of that of a circular tube[10].

Nouri-Borujerdi and Lavasani[11,12], Horvat et al.[13]summarized the results of related studies concerning the pressure drag coefficient and the Nusselt number around a streamlined single tube or a tubebundle. They found that all noncircular tubes have small drag coefficients and high Nusselt numbers as compared to circular tubes with the same circumferential length.

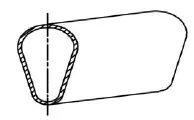
Fig.1 Drop-shaped tube

This paper proposes a new shape tube of easier production and higher pressure-bearing performance as compared with that of streamlined tubes mentioned in literature, which features an egg-shaped cross section composed of half a circle upstream and a semielliptic shape downstream. No mention is found of this new shape tube so far. In this paper, the characteristics of the flow and heat transfer around the new shape tube surface immersed in a thick, turbulent boundary layer are investigated both numerically and experimentally. Especially the influence of axis ratio, ε, on the heat transfer and the flow is determined for a better understanding of the mechanism and characteristics of the heat transfer enhancement of this new type tube.

1. Formulation and analysis

1.1 Physical model

The present analyses consider five infinitely long tubes with the egg-shaped cross section. The axis ratios, ε(≡L/ D), of these tubes are 1, 1.5, 2, 3, 4 and 5. To insure a same heat exchange area, they have a same circumference. The standard circular tube is represented by an axis ratio equal to 1. Figure 2(a) shows the cross-sections of the five tube shapes and the equivalent standard circular tube. Size parameters of the five tubes are listed in Table 1. L, D and S are the major axis, the minor axis of egg-shaped tubes and the distance along the body surface, respectively, as shown in Fig.2(b). For a proper comparison of the total drag and the heat transfer from egg-shaped tubes with different axis ratios, a suitable characteristic length is used in both the Reynolds and Nusselt numbers. The characteristic lengtheD is defined as the diameter of the equivalent standard circular tube.

As seen in Table 1, the cross sectional areas of the egg-shaped tube (1)ε＞ are smaller than that of the circular tube with an equal circumference, for example, the cross sectional area of tube E is only 52% of that of a circular tube with the same circumference. In other words, the heat transfer area of the tube’s outside part is much larger than that of a circular tube with the same cross sectional area. So the structure of the heat exchanger made of egg-shaped tubes can be more compact and the installation space needed is smaller.

1.2 Mathematical model

In order to simplify the numerical model, the following major assumptions are adopted in this study:

(1) Flow and heat transfer are two-dimensional and steady.

(2) Gravity and buoyancy lift is negligible.

(3) The thermo-physical properties of the air are constant and the local thermodynamic equilibrium is satisfied.

(4) Ambient temperature T∞is constant, and the flow is uniform with a constant velocity, U∞.

(5) The surface of tubes is smooth, and satisfies the no-slip velocity boundary conditions.

(6) In the case of an isothermal tube, the surface temperature of the wall is specified as wT with the radiation heat dissipation from the wall being neglected.

With the preceding hypotheses, the equations of continuity, momentum and energy for the two-dimensional incompressible flow around the tubes are, respectively, written as:

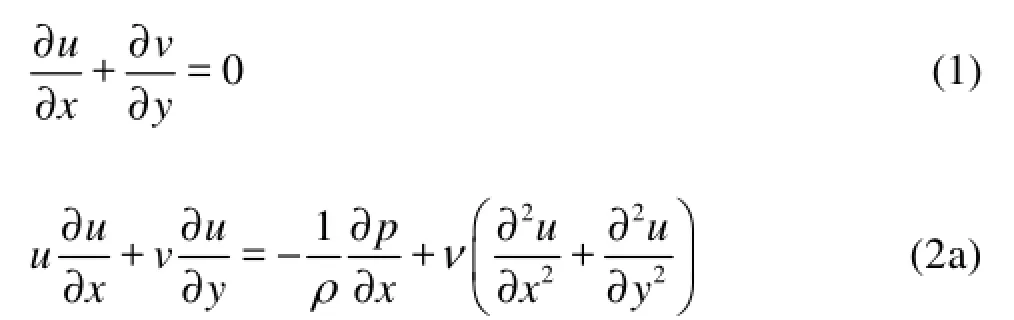
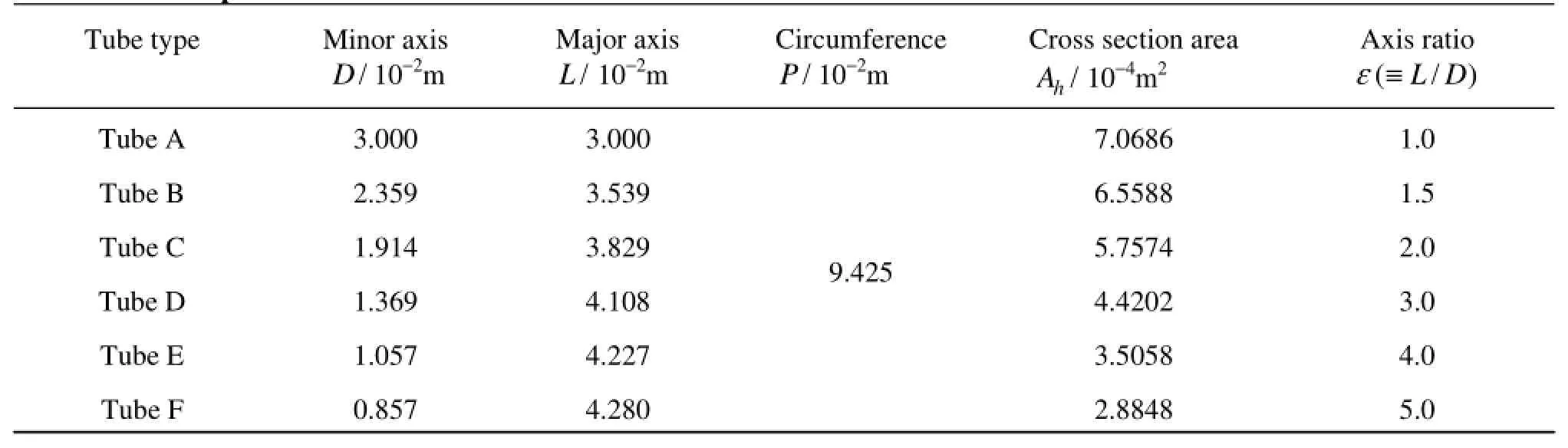
Table1 The size parameters for different tubes

where u, v are the component velocities in the -x and -y directions, respectively, ν, ρ, α and T are the kinematic viscosity, the density, the thermal diffusivity and the temperature of the air, respectively. Above equations are used to describe the turbulent flow problems, so the sympols u, v, p and T denote the instantaneous values of the corresponding pulsating physical quantities.

The RNG -kε turbulent model is selected for the turbulent calculation. The k equation and the ε equation in the RNG -kε model are as follows:

wherekG represents the generation of the turbulent kinetic energy due to the mean velocity gradients, 1Cε, C2εare the model constants and C1ε=1.42, C2ε= 1.68,ka and aεare the turbulent Prandtl number in the k equation and the ε equation, respectively, and Skand Sεare defined under practical conditions. Additional term Rεis the major difference between the RNG -kε model and the standard -kε model, which is given by

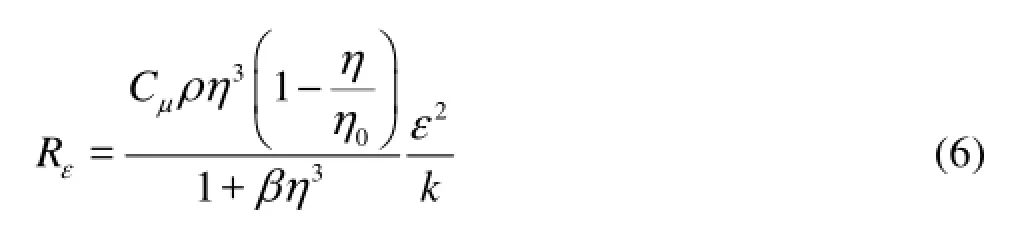
where η=Sk/ε, η0=4.38, β=0.012.

The RNG -kε model can produce a better response in the case of an instantaneous changing flow and a curved flow line with the function of additional term Rε, as compared with the standard -kε model. This is the reason why the RNG -kε model describes well the condition of a strong curved flow line, the vortex or rotating flow.

Fig.3 CFD Mesh of Tube C (tube with axis ratio, =2ε)

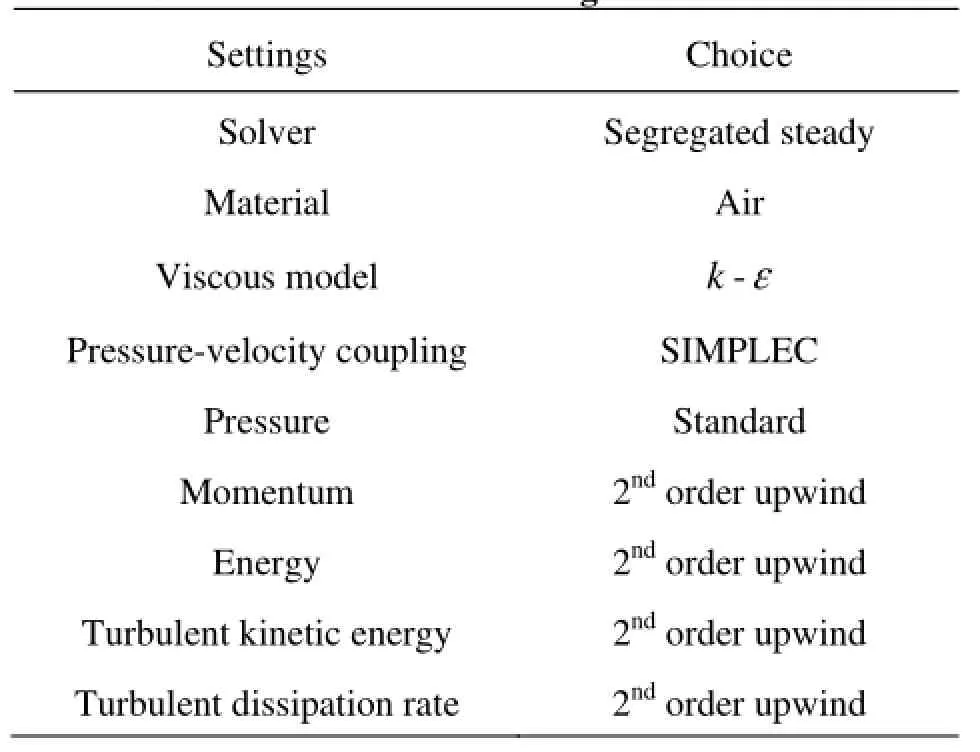
Table2 Numerical simulation settings

Fig.4 Wind tunnel system

1.3 Numerical resolution

1.3.1 Numerical methodologies

Equations (1)-(6), with the appropriate boundary conditions, are solved numerically by a commercial finite volume CFD code, Fluent. To minimize the effect of the far-field boundary conditions, the boundary of the computational domain must be placed sufficiently far away from the tube. A rectangular domain (lengh×width=40De×20De) is chosen to simulate the unbounded flow past the tubes in order to insure that the outer boundaries do not have any noticeable effect on the CFD simulation flow parameters. In the numerical model, a triangular mesh is used, and the area near the tube wall is carefully meshed by using a boundary layer technique to refine and minimize the grid size. This is necessary in order to observe the air flow around the tubes and to calculate the distribution of velocities and temperatures precisely near the wall. In Fig.3, the mesh of a tube with an axis ratio =2ε is illustrated.

Uniform incoming fluid velocity is set for the entry computation region. The range of the inlet velocity, U∞, is from 2 m/s to 24 m/s, with the inlet temperature, T∞, set as 293 K. Outer boundaries are set as adiabatic, with a no-slip boundary condition, and a constant surface wall temperature,wT, is equal to 353 K. The standard wall function method is adopted near the wall. Table 2 summarizes the simulation mode and the discretization conditions.

1.3.2 Mesh size independence and model validation

Several cases are tested with an increasing grid refinement to ensure that the solutions are independent of the mesh size. Four schemes to simulate a circular tube at Re=11952 are tested with a various number of grid elements (82 935, 95 408, 106 045 and 124 422 total grid elements). It is shown that the variation of the pressure coefficient,pC, for different grid schemes, is very small and the maximum relative error is only 1.78 %. So a grid scheme with 106 045 total mesh elements is chosen for use to optimize the computation time and the accuracy of the solution. In the same way, the mesh size independence for other egg-shaped tubes is tested.

From the studies of Zhukauskas and Ziugzda[14], the following correlation to calculate the dimensionless heat transfer for the flow around a circular tube is obtained

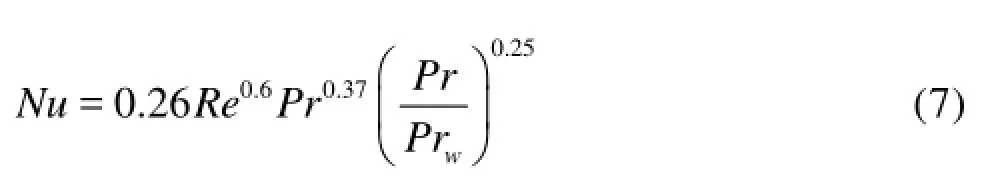
which is valid for Re=103-2× 105and where Nu= Deh/λ, Pr=ν/ α, Re=DeU∞/ν.

In order to validate the numerical model, the heat transfer of the circular tube is simulated, and an empirical correlation is obtained for the Reynolds number in the range Re=4 000-50 000 as

Comparing Eqs.(7) and (8), it is shown that the results of this study agree well with the results of Zhukauskas, indicating that the model and the method of the CFD simulation presented in this study is reasonable and reliable.

2. Experiment apparatus and technique

2.1 Experiment setup

A suction type wind tunnel constructed using acrylic resin boards is shown in Fig.4. Its test section cross section is 0.3 m×0.1 m.

A Pitot tube is mounted at the entrance of the test section to measure the velocity of the air. The pressure drop is determined by measuring the static pressure before and after the test specimen using a Testo 512 micromanometer connected to the pressure taps. The temperatures of the tube surface and the air in the test section are measured using copper-constantan thermocouples (Type T) calibrated by standard glass thermometers with a 0.01oC resolution.

The velocity detection using a Pitot tube is based on the Bernoulli’s equation

The mean air velocity in the test section can be obtained as

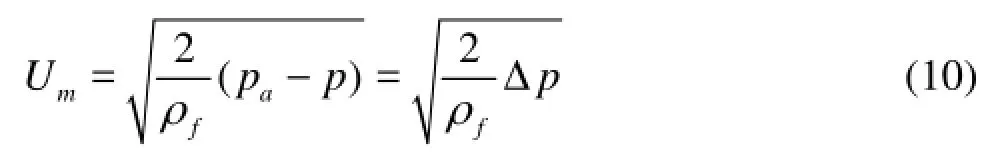
whereap is the stagnation pressure, p is the inlet pressure, fρ is the density of the inlet air,mU is the average velocity of the air in the test section.

Fig.5 Schematic diagram of the temperature measuring points on the tube surface and the air surrounded in the test section

The air temperature is measured at fourteen measuring points (numbered from 1 to 14), as shown in Fig.5, while the surface temperature of the tube is measured at eighteen points (numbered from 15 to 32).

The egg-shaped tubes made of cast aluminum (A, C, D, E) are tested experimentally using the same cross-section size as that used in the numerical simulation as shown in Table 1. The tube is electrically heated in order to produce the uniform heat flux boundary condition on the wall. Since the air flow is turbulent, the air is violently mixed there. Under the above condition, the influences of the uniform heat flux and the uniform wall temperature on the heat transfer can be considered as equivalent[15].

2.2 Data processing and reliability analysis

The experiments show that the air inlet temperatures of points from 8 to14 are nearly the same. That helps to define an effective heat transfer zone as shown by the dotted rectangle in Fig.5. The size of the dotted rectangle is 0.15 m×0.4 m. The heat absorbed by the air from the surface of the tube can be determined by calculating the enthalpy increase of the air between the inlet and the outlet.

where G, pc, outT and inT are the mass flowing through the effective heat exchange zone, the specific heat of the air, the outlet temperature and the inlet temperature, respectively.

The average temperatures of the inlet and the outlet of the air through the effective heat transfer zone can be calculated as follows:

The average temperature of the air in the test section can be calculated as

The average temperature of the tube surface can be calculated as

Then the average convective heat transfer coefficient on the air side can be obtained from the following equation

where the effective heat transfer area, A, of the tube is calculated as =APH, with P and H being the circumference of the cross section and the effective heating length of the tube, respectively,wT andfT are the average temperatures of the heated tube surface and the air in the test section, respectively.

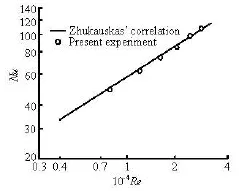
Fig.6 Comparison of Nusselt number of the experimental results and the empirical correlation of Zhukauskas

To assess the accuracy of the experiment results, the circular tube A with a diameter of 0.03 m and the effective heating length of 0.08 m is tested before evaluating the egg-shaped tube. Test results are compared with those in the literature. In Fig.6, a comparison of the experiment results between this study and the Zhukauskas’s correlation shows that the maximum deviation is 3.6%. This indicates that the results from this study agree well with an accepted empirical correlation, thus the feasibility and reliability of the measurement system is validated.

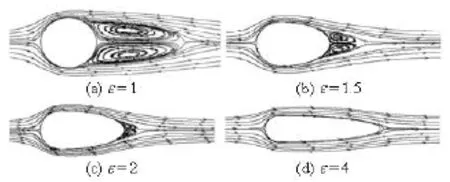
Fig.7 Comparison of streamlines for tubes of different axis ratios

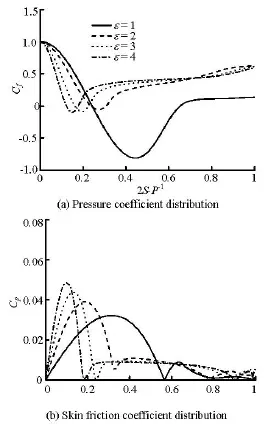
Fig.8 Pressure coefficient and skin friction coefficient of the tubes

3. Results and discussion

3.1 The characteristics of flow

The streamline diagrams at a Reynolds number of 31 872 for tubes with axis ratios of =ε1, 1.5, 2 and 4 are shown in Fig.7. It is clearly observed that the segregation point of the boundary layer moves backward when the axis ratio ε increases, and the segregation area is reduced. A pair of vortexes appears in the wake zone for the cases of =ε1, 2 and 3, with the size of the vortex gradually becoming smaller. When=4 ε the boundary layer has hardly any segregation and the wake zone almost disappears. This phenomenon suggests the varying of characteristics of the heat transfer and the fluid flow, when the air flows around the tubes with different axis ratios.

The pressure along the tube surface is expressed through a non-dimensional quantity,pC, known as the pressure coefficient. Since the distribution ofpC over tubes is symmetrical, only the pressure coefficient over a half surface of the tube is given in Fig.8(a). For different tubes, the value of allpC at the forward stagnation point is approximately equal to 1. Then it decreases along the circumference of the tube to reach a minimum value and then increases up to the rear stagnation point of the tube. The pressure coefficient, Cp, is strongly influenced by the axis ratio. At the frontal section, the pressure drop becomes sharper with the decrease of ε. The minimum value ofpC indicates the change from a favorable to an adverse pressure gradient over the tube surface. The minimum values ofpC occur at an angular position ofo80 for the circular tube. For elliptical tubes with 1ε＞, the minimum value ofpC takes place at a position angle smaller thano90, and as ε decreases, the angle necessary to provide the minimumpC decreases. For the case of the egg-shaped tube with =4ε, the higher favorable pressure gradient in the front of the tube and the lower adverse pressure gradient at the back of the tube help the flow to inhibit the separation.

The distributions of the skin friction coefficient Cffrom the forward stagnation point to the rear stagnation point of the tube, for tubes with differentε are plotted in Fig.8(b). The angular position of the maximum Cfshifts toward the forward stagnation point with the decrease of ε. A second zero value offC exists and indicates the boundary layer separation point from the tube surface, the location moves toward the rear stagnation point of the tube with the decrease of ε . The maximum value of Cf gradually increases with the increase of ε . A similar trend was reported by Schlichting[16] for values of ε including 1, 0.5, 0.25 and 0.125. Faruquee et al.[17] presented results for an elliptical tube for ε values of 0.75, 0.6, 0.5, 0.4 and 0.3.

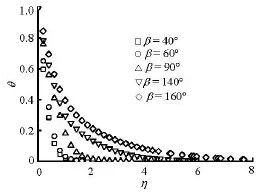
Fig.9 Distribution of the dimensionless excess temperature for an egg-shaped tube in the thermal boundary layer

Fig.10 Nusselt number distribution for different tubes

3.2 The characteristics of heat transfer

The dimensionless excess temperature variation for a tube with =2ε, at representative angular positions in the thermal boundary layer is plotted in Fig.9. The dimensionless temperature, θ, and the thermal boundary layer thickness increase with the increase of the position angle. The dimensionless temperature θ, is defined as follows

For different tubes at a Reynolds number of 31 872, the variations of the local dimensionless heat transfer coefficient along the wall of the tube are shown in Fig.10. It can be seen that the local heat transfer is influenced mainly by the thickness of the boundary layer of the flow, and that the heat transfer resistance increases with the development of the boundary layer. Therefore, the heat transfer coefficients are the largest at the forward stagnation point and then they decrease until the separation point of the boundary layer is reached. The separation point is shown as the lowest point of the curves in Fig.10, and going backwards from it, the heat transfer coefficient increases due to the occurrence of the vortex.

The variations of the average Nusselt number against the Reynolds number are shown in Fig.11 for tubes of different axis ratios. It is seen that the heat transfer performance of the egg-shaped tubes with= ε1.5, 2 and 3 is higher than that of a circular tube with =1ε, and the tube C with =2ε has the best heat transfer performance. When the Reynolds number is 3 984, the average Nusselt number of an eggshaped tube with =2ε is 13.8% higher than that of a circular tube, and 36.3% higher than that when the Reynolds number is 47 809. For the same Reynolds number and 2ε＞, the convective heat transfer coefficient decreases with the increase of ε, while at lower Reynolds numbers for 4ε≥, the Nusselt number of egg-shaped tubes is lower than that of a circular tube (=1)ε. That is because egg-shaped tubes with larger axis ratios allow the boundary layer to develop thicker, to generate a larger thermal resistance. Additionally, the separation point of the boundary layer moves backward, which reduces the influence of the vortex on the heat transfer enhancement.

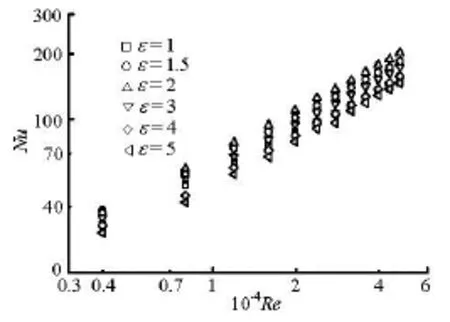
Fig.11 Variation of average Nusselt number against Reynolds number

From the simulation results, empirical correlations of dimensionless heat transfer coefficient for different tubes can be obtained:

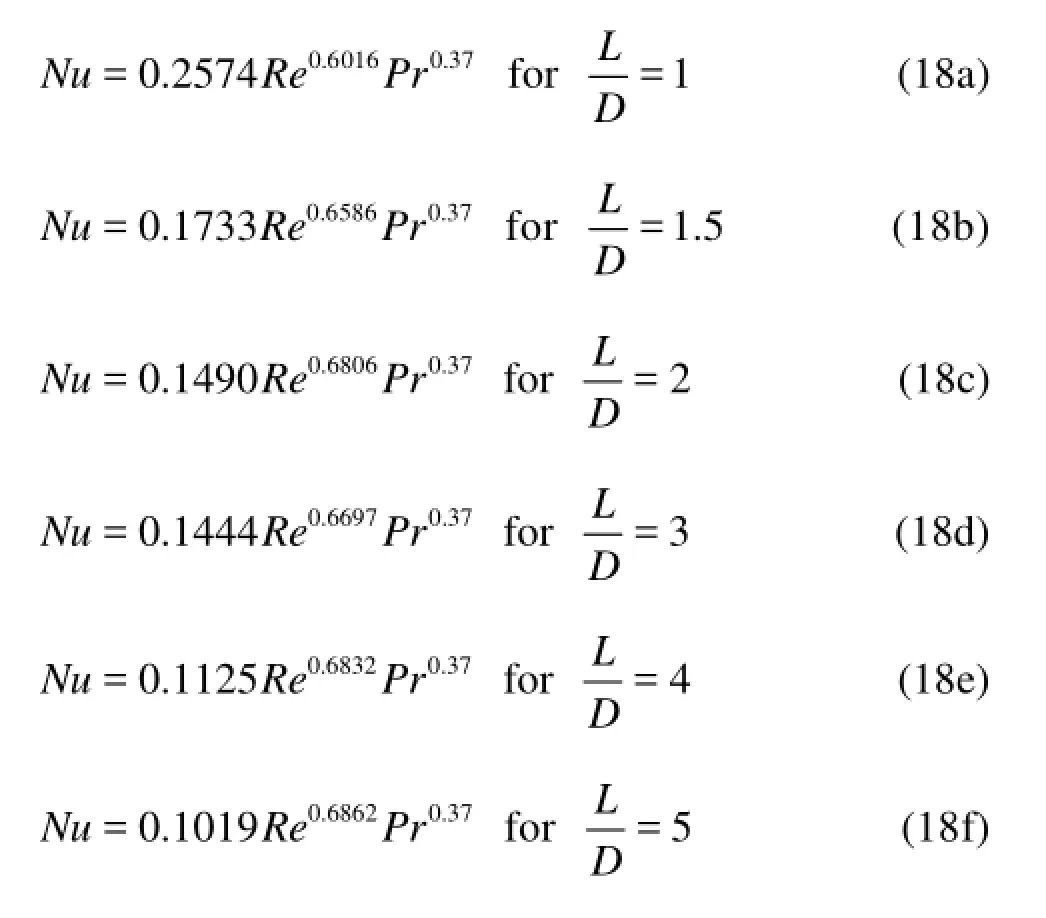
In the above formulas the characteristic dimensioneD is defined as the diameter of the equivalent circular tube for =1ε, whose perimeter is the same as that of other egg-shaped tubes. These results are for the Reynolds number in the range from 4 000 to 50 000.

3.3 Comprehensive evaluation

A performance evaluation criterion (PEC)[18]is adopted to evaluate the overall performance by using the heat transfer factor, j, and the resistance coefficient, f, and it can be defined as

where

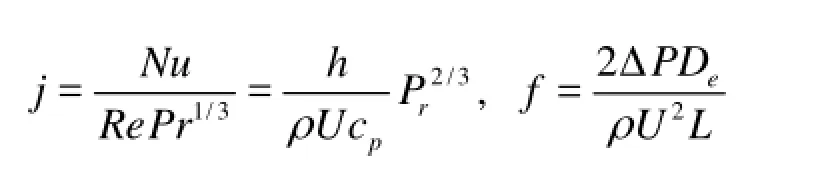
Figure 12 shows the variation of the PEC against the Reynolds number for different tubes. It is shown that the PEC of an egg-shaped tube (1)ε＞ is higher than that of the circular tube (=1)ε. The PEC of the egg-shaped tube with ratio ε of 2 is the best when 11952 Re＞, while the egg-shaped tube with ratio = ε3 has the best PEC when Re﹥11952 .

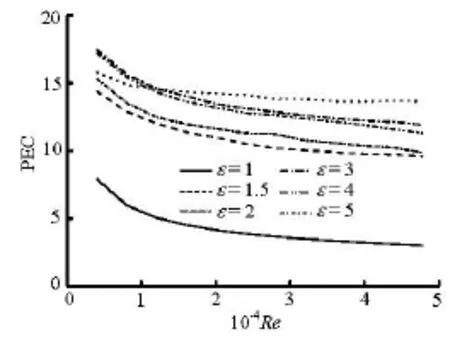
Fig.12 Variation of PEC against Reynolds number for different tubes

The variations of the PEC versus the axis ratio are shown in Fig.13 for different Reynolds numbers. It is found that the optimum shape of the tube varies with the Reynolds number. The PEC of an egg-shaped tube with 3.5ε≈ is the highest at the Reynolds numbers of 3 984, while for 2.2ε≈ the highest PEC is reached at the Reynolds number of 47 809. The highest point of the curve moves forward with Reynolds number increasing. In other words, the optimum value of the axis ratio ε of egg-shaped tubes decreases as the Reynolds number increases.

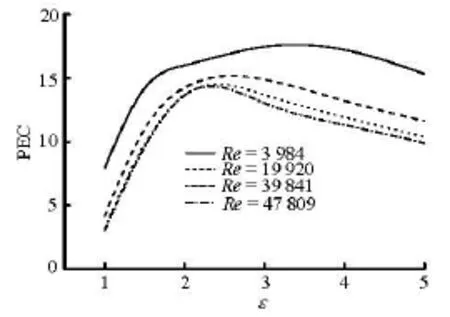
Fig.13 Variation of PEC against axis ratio for different Reynolds numbers

3.4 Reliability verification of study method

Experiment results for three different tubes with ε=2, 3 and 4 are shown in Fig.14. At a given Reynolds number, the egg-shaped tube with =2ε has the better performance of heat transfer than that of the other tubes, which agrees well with the numerical results. With other tubes’ results included, the largest difference between the experimental results and the numerical data is 4.1% (as shown in Fig.14).

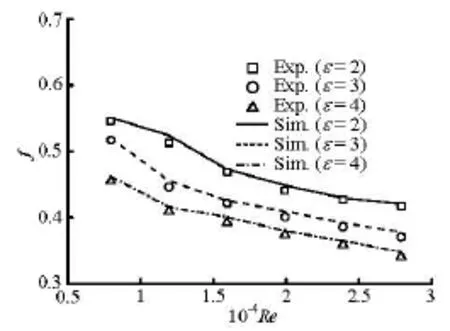
Fig.15 Comparison of the total drag coefficients for experimental and numerical results

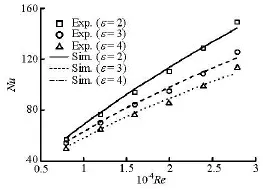
Fig.14 Comparison of average Nusselt number for experimental and numerical results

Experimental data for the variation of the totaldrag coefficients against the Reynolds number for egg-shaped tubes are shown in Fig.15. A comparison to the results from a numerical simulation is also given. The distribution of the experimental total drag coefficients agrees well with the numerical results. The totals drag coefficients decrease with the increase of the axis ratio ε for all tubes. Experimental drag coefficients are only slightly smaller than those obtained by numerical simulations.

The above discussion has verified the effectiveness and correctness of the numerical method employed in this paper.

4. Conclusions

The effects of the axis ratio ε on the flow and heat transfer characteristics around a new type eggshaped tube are investigated by both numerical simulations and experiments. The main conclusions are as follows:

(1) Streamline diagrams for tubes with different axis ratios are shown, and the wake size decreases as ε increasing.

(2) Egg-shaped tubes have a high, favorable pressure gradient at the front of the tube and a low, adverse pressure gradient in the back of the tube, which helps the flow in inhibiting an early separation. The position angle of the minimum value ofpC decreases as ε decreasing. The maximum value offC gradually increases with ε decreasing.

(3) The overall performance is evaluated by the PEC evaluation criterion and it is found that an eggshaped tube, with =2ε has the best overall performance when Re＞11952.

(4) To verify the effectiveness and correctness of the numeric model utilized, an experimental study is carried out for tubes with =ε1, 2, 3 and 4. Experimental results agree well with those of the numerical simulations.

[1] KHAN W. A., CULHAM R. J. and YOVANOVICH M. M. Fluid flow around and heat transfer from elliptical tubes: Analytical approach[J]. Journal of Thermophysics and Heat Transfer, 2005, 19(2): 178-185.

[2] MATOS R. S., VARGAS J. V. C. and LAURSEN T. A. et al. Optimization study and heat transfer comparison of staggered circular and elliptic tubes in forced convection[J]. International Journal of Heat and Mass Transfer, 2001, 44(20): 53-61.

[3] MATOS R. S., VARGAS J. V. C. and LAURSEN T. A. et al. Optimally staggered finned circular and elliptic tubes in forced convection[J]. International Journal of Heat and Mass Transfer, 2004, 47(6-7): 1347-1359.

[4] CASTIGLIA D., PAPADAKIS G. and BALABANI S. et al. An experimental and numerical study of the flow past elliptic cylinder arrays[J]. Proceedings of the Institution of Mechanical Engineers, Part C-Journal of Mechanical Engineering Science, 2001, 215(11): 1287-1301.

[5] CASSTIGLIA D. Fluid flow and heat transfer in unconventional tube bundle arrangements in crossflow[D]. Doctoral Thesis, London, UK: University of London, 2002.

[6] LI Z., DAVIDSON J. H.and MANTELL S. C. Heat transfer enhancement using shaped polymer tubes: Fin analysis[J], Journal of Heat Transfer, 2004, 126(2): 211-218.

[7] MOHARANA M. K., DAS P. K. Heat conduction through heat exchanger tubes of noncircular cross section[J]. Journal of Heat Transfer, 2008, 130(1): 011301.

[8] DUTTA A., SOM S. K. and DAS P. K. Film condensation of saturated vapor over horizontal noncircular tubes with progressively increasing radius of curvature drawn in the direction of gravity[J], Journal of Heat Transfer, 2004, 126(6): 906-914.

[9] BADR H., DENNIS S. and KOCABIYIK S. Numerical simulation of the unsteady flow over an elliptic tube at different orientations[J]. International Journal for Numerical Methods in Fluids, 2001, 37(8): 905-931.

[10] CHENG S., ZHAO Y. and CHEN G. Experimental study of heat transfer and flow resistance of air across a droplet-shaped tube[J]. Journal of Engineering Thermophysics, 1988, 9(4): 359-361.

[11] NOURI-BORUJERDI A., LAVASANI A. M. Experimental study of forced convection heat transfer from a cam shaped tube in cross flows[J]. International Journal of Heat and Mass Transfer, 2007, 50(13): 2605-2611.

[12] NOURI-BORUJERDI A., LAVASANI A. M. Pressure loss and heat transfer characterization of a cam-shaped tube at different orientations[J]. Journal of Heat Transfer, 2008, 130(12): 124503.

[13] HORVAT A., LESKOVAR M. and MAVKO B. Comparison of heat transfer conditions in tube bundle crossflow for different tube shapes[J]. International Journal of Heat and Mass Transfer, 2006, 49(5-6): 1027-1038.

[14] ZUKAUSKAS A., ZIUGZDA J. Heat transfer of a tube in crossflow[M]. New York, USA: Hemisphere Publishing, 1985.

[15] YANG Shi-ming, TAO Wen-quan. Heat transfer[M]. 4th Edition, Beijing, China: Higher Education Press, 2006, 244(in Chinese).

[16] SCHLICHTING H. Boundary-layer theory[M]. New York, USA: McGraw-Hill, 1979.

[17] FARUQUEE Z., TING D. S. K. and FARTAJ A. et al. The effects of axis ratio on laminar fluid flow around an elliptical tube[J]. International Journal of Heat and Fluid Flow, 2007, 28(5): 1178-1189.

[18] PROMVONGE P., EIAMSA A. S. Heat transfer enhancement in a tube with combined conical-nozzle inserts and swirl generator[J]. Energy Conversion and Management, 2006, 47(18-19): 2867-2882.

10.1016/S1001-6058(15)60458-9

* Project supported by the Science and Technology Development Planning of Shandong Province (Grant No. 2012GGX10421).

Biography: ZHANG Guan-min (1973-), Male, Ph. D., Professor

LENG Xue-li, E-mail: lengxl@sdu.edu.cn

Fig.2 Cross-sections of egg-shaped tubes