轨道车辆行李架托架的材料模型与实验修正
2015-02-16秦建忠姚春斌张智
秦建忠,姚春斌,张智 杰
(1.今创集团股份有限公司,常州 213 000; 2.天津航天瑞莱科技有限公司上海分部,上海 201100)
轨道车辆行李架托架的材料模型与实验修正
秦建忠1,姚春斌2,张智 杰2
(1.今创集团股份有限公司,常州 213 000; 2.天津航天瑞莱科技有限公司上海分部,上海 201100)
以行李架托架为例,采用双线性弹塑性模型,利用有限元方法对行李架托架强度进行了校核,比较直观地了解行李架托架的应力分布,并通过实验修正相关参数,为行李架托架后续分析提供了基础。
行李架托架;有限元;双线性弹塑性模型
概述
行李存放是旅客列车设计中的重要课题,合理解决行李存放也是体现旅客列车“人性化服务的重要标志”。在保证可靠安全的前提下,怎样在有限的空间内最大限度地满足旅客行李存放的需求,并且做到美观化、轻量化、模块化是行李架设计不断追求的目标。我国铁路旅客列车的行李存放一般有行李台、行李架和大件行李存放三种方式。其中行李架的设置最为普遍,广泛应用于普通客车和高速动车上[1]。其中行李架托架是支撑整个行李架和行李的关键部件,本文以行李架托架为例,利用有限元方法对行李架托架进行校核,并通过实验作验证对比和修正。

图1 行李架托架三维模型
行李架托架位于行李架两端,端部和车体接口相连,主要由两部分组成,端部铸件(ZL115-T5)和拉杆(6063-T5),其三维模型示意见图1。
1 双线性弹塑性模型
在金属弹-塑性大变形问题分析中,需要考虑材料的非线性。材料非线性又称为物理非线性,它研究的是金属塑性变形过程中应力与应变之间的非线性物理关系,即本构关系。常见金属材料的应力应变曲线如图2所示,简化而成的双线性弹塑性模型如图3所示。双线性弹塑性模型在弹性阶段其应力-应变曲线的斜率即为弹性模量,而在过了屈服点之后的塑性阶段斜率即为应变硬化模量,也是一个定值。
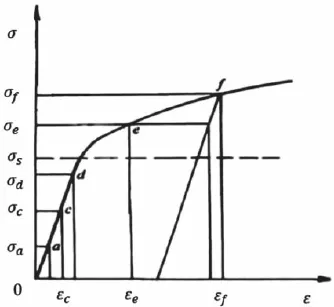
图2 某材料的应力-应变曲线

图3 双线性弹塑性模型的应力-应变曲线
2 行李架托架的破坏实验
为了考察行李架托架的静强度,本文进行了行李架托架的破坏实验。将试验件按照实际承载状态安装在工装上,通过气缸和加压板对行李架托架前端施加载荷,逐渐增大施加的压力,试验件开始发生形变直至断裂,同时记录下整个实验过程中的载荷数据。实验重复进行了三次,实验状态及系统示意见图4,三次实验的载荷曲线以及试验件的断裂状态见图5和图6,由此得到的行李架托架破坏时承受的极限力信息如表1所示。

表1 行李架托架的极限力信息

图4 行李架托架破坏实验
3 有限元分析
行李架托架的有限元模型通过MSC.Patran 2012创建,采用Tet4自由划分网格,单元的全局尺寸为3mm,最小尺寸为0.6mm,整个模型单元数共115671个。行李架固定端采用位移约束固定,并在前端受力曲面处施加1350N(三次破坏实验得到的加载极限的平均值)的均布载荷,有限元模型见图7。
由于行李架最终会发生破坏,所以在整个过程中的材料属性是非线性的,本文采用双线性弹塑性模型来模拟,并和单线性模型作对比。根据表2给出的材料属性,有限元分析时选用各向同性的弹塑性模型,对于拉杆型材,其原始硬化模量(Hardening slope)可取为1059MPa[2],屈服点(Yield Point)为130MPa;对于端部铸件,硬化模量也取为1059MPa,屈服点为280MPa,最终根据试验结果得到修正后的硬化模量为28000MPa。计算结果见表3,有限元应力云图见图8~图10。
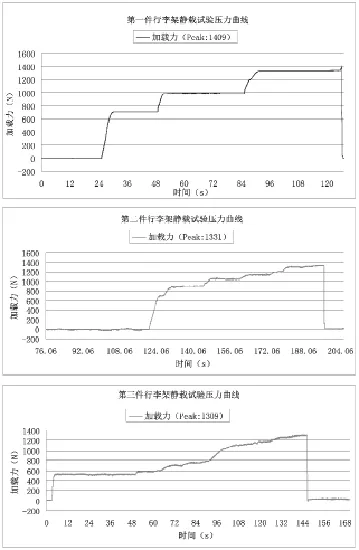
图5 三次行李架破坏实验的加载曲线

图6 三次行李架破坏实验的断裂位置

图7 行李架托架有限元模型
4 结论
行李架托架的破坏试验表明,当托架前端受力为1350N左右时,托架发生断裂破坏,断裂点一致都为拉杆和底架连接处靠近受力端一侧。

表2 材料属性
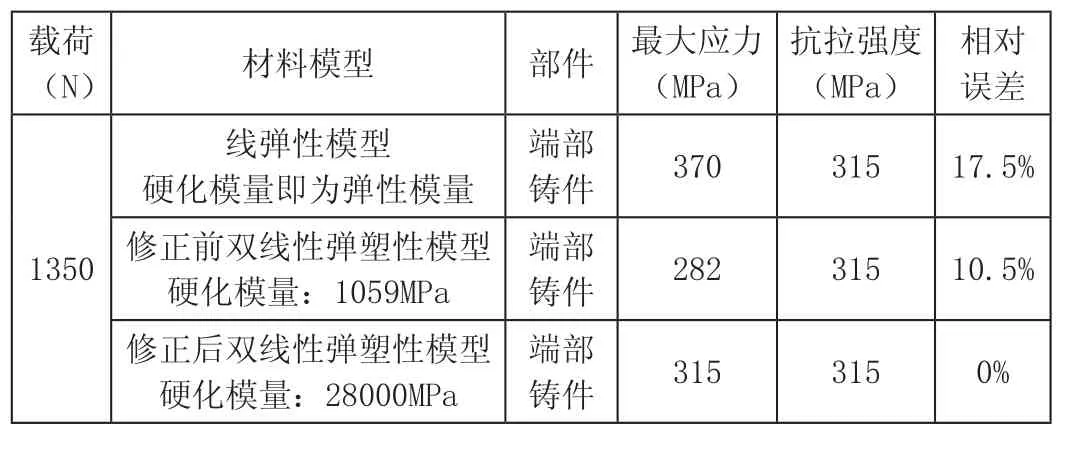
表3 有限元结果汇总

图8 线弹性模型的计算结果

图9 修正前的双线性弹塑性模型的计算结果

图10 修正后的双线性弹塑性模型的计算结果
有限元计算的结果表明,同样施加由于线弹性模型在屈服点之后的切线模量要大于真实的硬化模量,因此计算出的最大应力偏大,超过了材料的断裂极限;修正前的双线性弹塑性模型由于硬化模量的取值偏小,因此得到的最大应力偏小,小于材料的断裂极限;修正后的双线性弹塑性模型得到了与实验相一致的最大应力以及断裂位置。因此这个模型可以应用于相同试验件的其他有限元分析中。
[1] 陈贺久. 轨道车辆行李架结构强度分析[J]. 中国科技博览, 2014,(26):45.
[2] 范秀昌. 应变硬化模量确切意义与实验测法及其应用算例[J]. 天津大学学报, 1999,32(04):504-507.
[3] 范秀昌. 应变硬化模量的实验测量与计算[J]. 天津理工学院学报,1998,(1)1-4.
[4] 杨锋平. 屈服准则及切线模量修正的弹塑性计算模型[J]. 力学学报, 2010,(04):804-810.
[5] 张志平. 广义切线模量理论及其应用[D]:[博士学位论文]. 哈尔滨:哈尔滨工程大学. 2005.
秦建忠(1966.7-),大专(东南大学 机械铸造专业)、本科(南京大学 经济管理专业),工程师,主要研究方向:轨道交通产品可靠性。
姚春斌(1988.6-),本科(复旦大学 力学)、硕士(同济大学 力学),助理工程师,主要研究方向:测试技术,模态分析。
张智杰( 1988.4-),本科(北华航天工业学院机械设计及自动化),助理工程师。
The Material Model and Experimental Correction of Rail Vehicle Luggage Rack Bracket
QIN Jian-zhong1, YAO Chun-bin2, ZHANG Zhi-jie2
(1. KTK GROUP Co., Ltd., Changzhou 213000; 2.Tianjin Aerospace Ruilai Technology Co. Ltd., Shanghai 201100)
Taking the example of the luggage rack bracket, this paper uses the finite element method to check the strength of with bilinear elastoplastic model; then the stress distribution of luggage rack bracket is intuitively under stood. Finally, it corrects the harden slope according to the experiment result and provides the basis for the subsequent analysis of the luggage rack bracket.
luggage rack bracket; finite element; bilinear elastoplastic model
O341
A
1004-7204(2015)01-0021-04
