基于滑移率变化模型的ABS汽车制动距离计算

沈 晨，秦训鹏，刘昌业，何 东，吴天昊

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070;2.现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070;3.上汽通用五菱汽车股份有限公司，广西 柳州 545007)



基于滑移率变化模型的ABS汽车制动距离计算

沈 晨1,2，秦训鹏1,2，刘昌业3，何 东1,2，吴天昊1,2

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070;2.现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070;3.上汽通用五菱汽车股份有限公司，广西 柳州 545007)

为探讨新的ABS汽车制动距离计算方法，分析了汽车制动过程前、后车轮受力状况，建立了以各车轮滑移率余弦变化模型计算汽车制动距离的数学方法，在潮湿的混凝土路面上进行制动试验，应用Matlab软件仿真计算汽车在不同制动初速度下的制动距离。研究表明，仿真计算制动过程中车速和制动距离随时间的变化历程与试验测量值接近，制动时间和制动距离的计算值与测量值偏差较小，证明了计算模型的可靠性。

ABS汽车；滑移率；制动距离；制动时间；潮湿路面

汽车制动距离是指在一定制动初速度下，驾驶员从踩制动踏板开始至车辆停止时所驶过的距离，其直接影响着行车安全，是评价汽车制动性能的重要指标[1]。装备了ABS防抱死制动系统的汽车(以下简称ABS汽车)在制动时其前后车轮都处于边滚边滑状态，其制动距离的计算分析较车轮抱死拖滑时更为复杂。

对于ABS汽车制动距离的研究，国外有学者通过数值解析方法估算防抱死制动系统的制动距离，并对轮胎滚动三维动态模型进行了分析[2]。国内的研究通常通过系统仿真模拟建立轮胎和车辆的动力学或有限元模型来进行[3-4]，这种方法对模型精确度的要求较高，效率低。在利用理论公式计算ABS汽车制动距离方面，王润琪等利用能量守恒原理计算了车辆在平路和坡道上的制动距离[5]；熊五沅假设制动减速度呈线性变化或简单的三角函数变化进行分析[6]，这种直接对减速度变化进行拟合的计算方法缺乏理论依据，具有一定的局限性；同时，上述方法虽然便于制动距离的计算，却缺少试验支撑，与实际情况也存在一定的差距。

笔者通过分析制动过程中车辆的受力状况、滑移率与地面制动力的关系，以及ABS作用过程中车轮滑移率的变化特征，建立了基于车轮滑移

率变化值的车辆制动距离的简化计算模型，并将模型计算结果与实车试验数据进行对比分析，以验证计算模型的可靠性。

1 汽车制动距离数学模型的建立

1.1 汽车受力分析

图1是质量为M的汽车在水平路面上制动时的受力情形，FZ1和FZ2分别为地面对前、后轮的法向反作用力，FXb1和FXb2分别为前轮和后轮的地面制动力，G为汽车重力，h为汽车质心高度，a为汽车质心至前轴中心线的距离，b为汽车质心至后轴中心线的距离，L为汽车轴距，v为汽车行驶速度。汽车受力分析时，忽略了空气阻力、汽车的滚动阻力矩、旋转质量减速时产生的惯性力矩及车轮边滚边滑过程中产生的滚动力矩的影响。根据力的平衡条件，分别对汽车前轮和后轮接地点取力矩，可得：

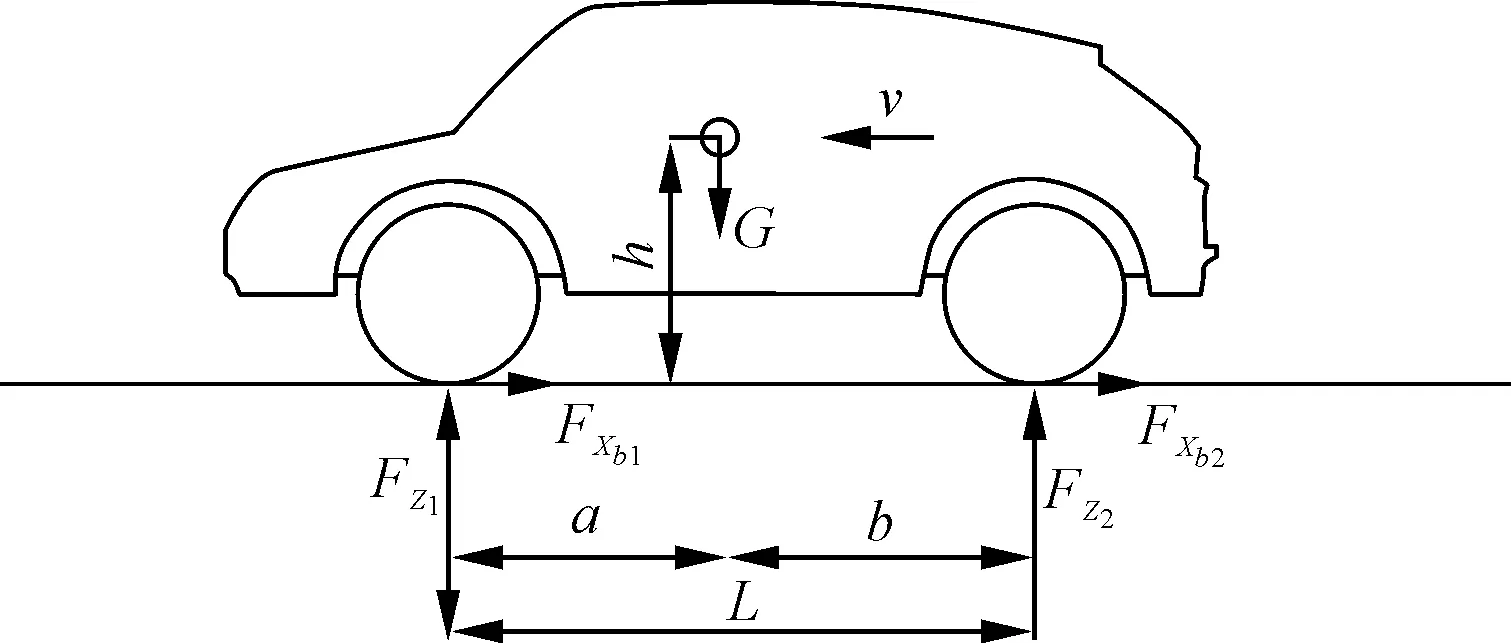
图1 制动时的汽车受力

(1)

对汽车行驶方向进行动力学分析，可得：

(2)

1.2 ABS汽车制动距离的计算

ABS汽车以v0为初速度紧急制动可以分为4个阶段，其制动过程示意图如图2所示，其中Fp和ab分别为制动过程中理想的踏板力和车辆减速度值。一般所指的制动距离包括制动器起作用和持续制动两个阶段中汽车驶过的距离，制动时间为两个阶段的时间之和，即制动时间ta=t2+t3。

图2 汽车制动过程示意图

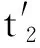
(3)

在持续制动阶段t3时间内，认为ABS处于工作状态，根据滑移率的变化特征[7]，取各车轮滑移率的变化为时间的余弦函数，前左、前右、后左、后右车轮的滑移率变化周期依次为T1、T2、T3、T4，各车轮的滑移率波动幅值分别为A1、A2、A3、A4，目标值均为A0，即可拟合得到各个车轮滑移率随时间t的变化公式为：

(4)

决定汽车制动距离的主要因素有制动器起作用时间、附着力及起始制动车速，同时，制动过程中受路面附着力限制的地面制动力起着决定性作用，其是使汽车制动而减速行驶的外力。附着系数的数值主要取决于道路的材料、路面的状况与轮胎结构、胎面花纹与材料，以及汽车运动的速度等因素，当行驶工况一定时，可将其取为定值。由于滑移率与制动力系数关系要用曲线才能精确拟合，计算量较大，不适宜实时控制，为了获得简单的解析解，用双直线来拟合，得到滑移率与制动力简化模型，如图3所示，定量关系式如式(5)所示。

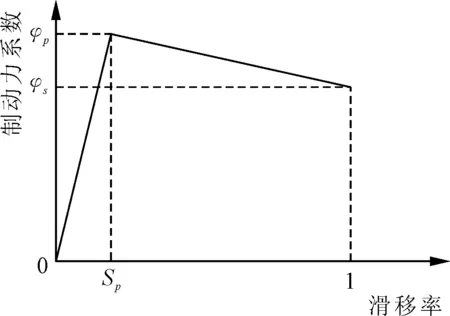
图3 滑移率与地面制动力简化模型

(5)

结合式(4)和式(5)，可得持续制动阶段各个车轮的制动力系数为：

(6)

制动力系数为地面制动力与垂直载荷之比，可得前后轮的地面制动力分别为：

(7)

再联立式(1)、式(2)和式(7)可解得车辆瞬时减速度为：

(8)

对式(8)积分可得到车速v为：

(9)

再对式(9)积分得到车辆行驶距离D为：

(10)

令v=0，解得持续制动时间t=t3,持续制动阶段的制动距离D2为：

(11)

联立式(3)和式(11)即可得到车辆总的制动距离为：

(12)

2 试验与计算结果对比分析

2.1 ABS汽车制动性能试验

参照《乘用车制动系统技术要求及试验方法》(GB21670-2008)的要求，设计制动试验方案，为了检验ABS的性能及能够提供较大的附着力，选择在潮湿的平直混凝土路面上进行试验，制动性能检测设备为VBOX数据采集系统，并在4个车轮上加装轮速传感器。试验分别以制动初速度50km/h、60km/h、72km/h、90km/h(理想状态)进行，每种试验将两种轮胎在同一路段进行测试，并取两次试验结果的平均值，以尽可能剔除轮胎对附着系数的影响。试验车辆为某微型车，制动器为前轮盘式、后轮鼓式。在制动试验前，还需注意以下几点准备工作。

(1)汽车油箱加至厂定容积的90%，加满冷却液和润滑剂，试验加载为200kg(驾驶员、1名试验员和仪器质量)。

(2)轮胎为经磨合后的新胎，胎压为厂定压力，绝对误差不超过10kPa。

(3)制动系统的部件按制造厂的规定进行装配和调整，制动过程中发动机脱开。

做好试验准备工作后，按照试验方案进行道路制动试验，试验环境及制动性能检测结果参数分别如表1和表2所示。

表1 试验环境

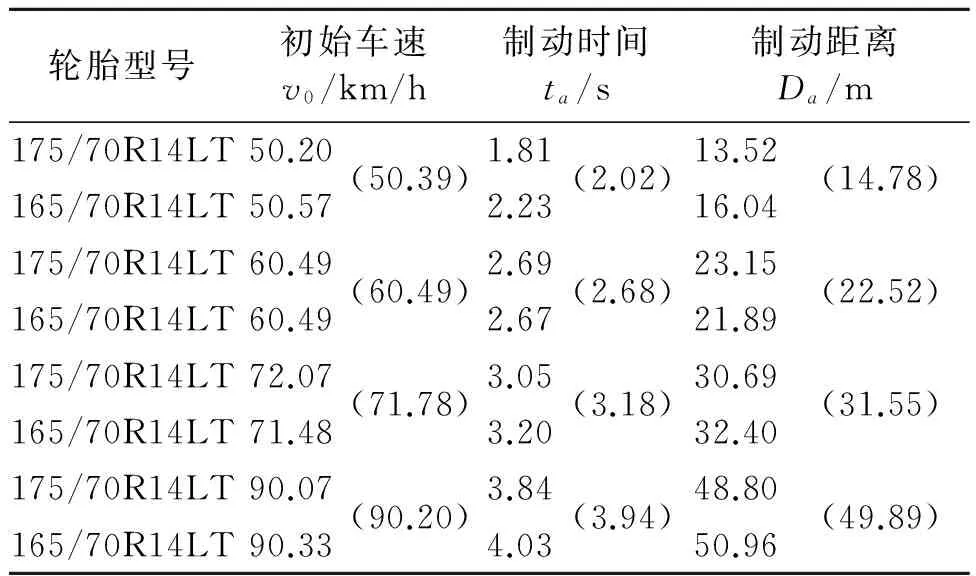
表2 制动性能检测结果参数

注：()内为两种轮胎试验结果的平均值

2.2 制动距离仿真计算

如图4所示为所采集的车辆以60km/h为初速度进行制动试验时两前轮和两后轮的轮速变化曲线，经过分析可认为其变化频率为定值，故当制动过程中车速单调减小时其滑移率的变化频率也为同一定值，与所提出的滑移率变化模型吻合，且此时两前轮之间和两后轮之间的滑移率变化特征可认为相同。取图4中各车轮轮速曲线波谷点，并对相邻两波谷点的时间间隔取平均值，即得到理想状态下前后轮滑移率变化的周期分别为0.16s和0.35s。一般情况下，车轮的滑移率为10%～30%时车辆能达到最佳的制动效果[8]，模型中选取20%作为ABS控制滑移率的目标值[9]，并由测量得到前后轮轮速变化的幅值和车轮滑移率变化范围，选定前后轮滑移率的幅值为10%和15%。由此得到滑移率变化的计算模型如图5所示，图5中时间范围为持续制动阶段开始的1s内,前后轮滑移率计算模型的公式为:

(13)

(14)

滑移率模型确定后根据上述制动器起作用阶段车速和加速度的变化特征，以及持续制动阶段车辆的速度v和行驶距离D的计算式，利用Matlab编写计算程序，对试验车辆制动过程中的速度和行驶距离进行计算。模型中的基本参数见表3。为方便与试验结果进行对比分析，仿真初速度为试验设定的初速度。模型中的滑动附着系数φs和峰值附着系数φp取各种潮湿混凝土路面上的平均附着系数的值，分别为0.7和0.8。

图4 轮速变化测试结果

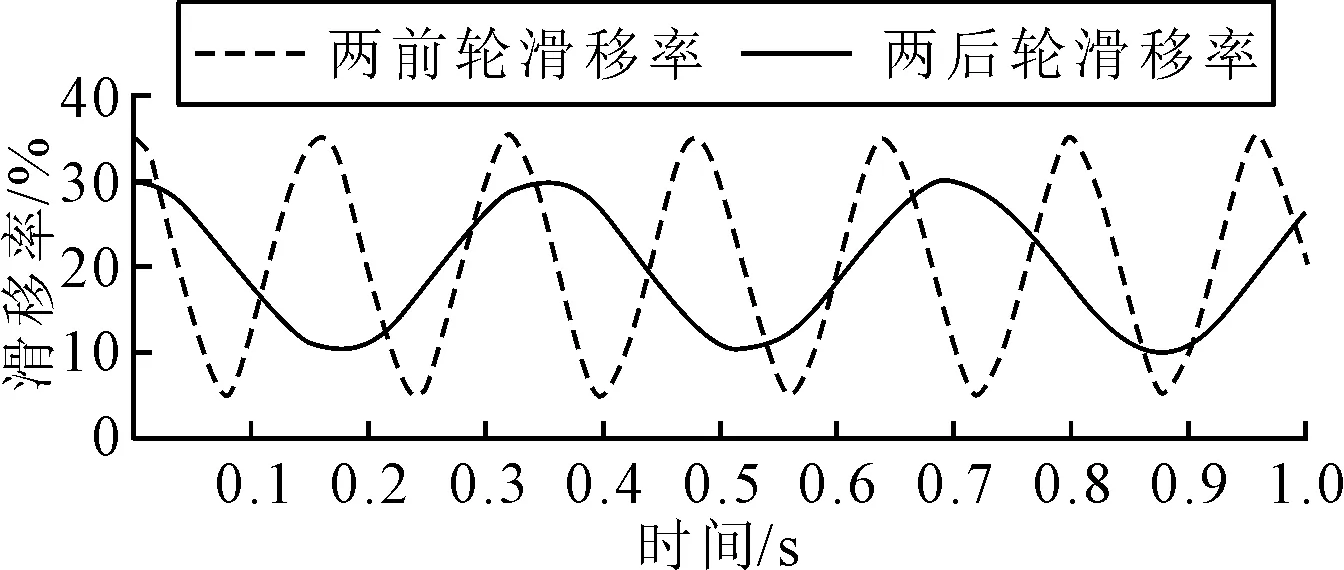
图5 滑移率计算模型

2.3 试验与计算结果对比

装载165/70R14LT轮胎的试验车辆在4种初始车速条件下制动过程中车速和行驶距离变化曲线的试验结果和计算仿真结果如图6所示，总的制动时间ta和制动距离Da的试验值与仿真计算值对比见表4。

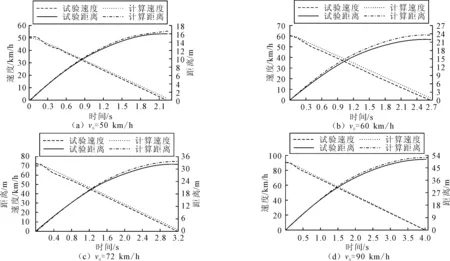
图6 不同初始车速条件下制动速度与距离的试验结果与计算结果对比

表4 计算结果与试验结果对比情况

由图6和表4可知，计算制动过程中车速和制动距离随时间的变化历程与试验测量值接近，制动时间和制动距离的计算值与测量值偏差较小，特别是当制动初速度较高时，实际制动距离变化与计算仿真结果吻合度较高。而由于路面附着系数和ABS控制滑移率变化的周期及范围随着不同路面条件和工况在一定范围内变化等因素的影响，导致汽车以不同制动初速度计算时与试验值出现一定的偏差，但依然在合理范围内。

3 结论

通过对车轮滑移率变化曲线进行拟合，提出了基于滑移率变化的车辆制动距离计算模型，根据实测值确定拟合的相关参数，用Matlab进行了仿真计算，并在潮湿的混凝土路面上进行不同初始车速下车辆的ABS制动试验，得到的结果与计算值较为吻合。在车速较高的情况下，不同车速制动距离的误差控制在7%以下。因此，笔者所提出的计算方法和建立的仿真模型较可靠，特别适用于较高车速的情况。

在获得ABS控制特性基础上，ABS车辆制动距离的计算方法可用于估算某一车型在不同路面状况下不同制动初速度紧急制动时的制动距离，模拟出不同路面状况的汽车制动效能情况。该滑移率模型和计算方法，可以为车辆ABS对滑移率控制的进一步研究提供参考，而且由于其在较高车速范围内准确度更高，其结果可为路面状况较差的路面，如湿滑路面的交通肇事责任认定提供判定依据，也可为路面限速提供参考。

[1] 余志生.汽车理论[M].北京：机械工业出版社，2009：89-129.

[2] CHO J R，CHOI J H，YOO W S，et al.Estimation of dry road braking distance considering frictional energy of patterned tires[J].Finite Elements in Analysis and Design，2006(42)：1248-1257.

[3] 王珂晟，宗磊强，曹琪，等.基于虚拟样机的战地越野车整车制动仿真分析[J].计算机仿真，2011,28(8)：342-347.

[4] 臧孟炎，陆波，陈玉祥.干燥路面上轮胎制动距离的FEM仿真[J].汽车工程，2011,33(2)：156-161.

[5] 王润琪，蒋科军.ABS汽车制动距离分析与计算[J].中南林学院学报，2005,25(2)：70-73.

[6] 熊五沅.ABS汽车制动性能模拟计算与评价研究[D].上海：华东交通大学，2012.

[7] 孙陈迪，过学迅，裴晓飞，等.基于Labcar的ABS控制器HIL测试[J].武汉理工大学学报(交通科学与工程版)，2014,38(6)：1358-1361.

[8] 郑太雄，马付雷.基于逻辑门限值的汽车ABS控制策略[J].交通运输工程学报.2010，10(2):69-74.

[9] 严运兵，吴浩，赵慧.汽车防抱死制动系统的鲁棒控制[J].汽车工程，2014，36(4)：453-458.

SHEN Chen:Postgraduate; School of Automotive Engineering, WUT, Wuhan 430070, China.

[编辑：王志全]

Braking Distance Calculation of ABS Automobiles Based on Variation Model of Wheel Slip Rate

SHENChen,QINXunpeng,LIUChangye,HEDong,WUTianhao

In order to put forward a new ABS automobile braking distance calculation method, the forces conditions of front and rear wheels during automobile braking process were analyzed. And a mathematical method was established to calculate the braking distance based on the cosine change model of wheel slip rate. Braking tests were carried out on the wet concrete road surfaces; and the MATLAB was applied to calculate the automobile braking distance under different primary braking speed. Experimental result shows that on the wet concrete road surfaces, the changing time history of speed and braking distance calculated by simulation matches well with that measured during test; the deviation between calculated value and the test value of braking time and braking distance is small; therefore, the calculation model is reliable.

ABS automobiles; wheels slip rate; braking distance; braking time; wet pavement

2015-07-07.

沈晨(1991-)，男，湖北孝感人，武汉理工大学汽车工程学院硕士研究生.

湖北省科技支撑计划基金资助项目(2012BAA08001);湖北省自然科学基金资助项目(2013CFA136).

2095-3852(2015)06-0865-05

A

U462.32

10.3963/j.issn.2095-3852.2015.06.044