基于Matlab的C2,C3类气体压缩机功率求解

沈顺成，何 博，黎章杰

(武汉理工大学 机电工程学院，湖北 武汉 430070)



基于Matlab的C2,C3类气体压缩机功率求解

沈顺成，何 博，黎章杰

(武汉理工大学 机电工程学院，湖北 武汉 430070)

对于传统功率计算不适合C2，C3类压缩机在临界参数附近工作时的问题，通过对比态原理和一系列实际气体状态方程，推导出绝热指数k值的公式并推出更具普遍性的功率计算关系式，并通过Matlab编写出计算程序，成功运用到C2，C3类压缩机的功率求解上。

C2和C3类压缩机;绝热指数；Matlab；功率求解

某石油化工厂的乙烯增压压缩机投入实际生产后出现超负荷运行状况，压缩机额定功率为870 kW，驱动机额定功率为1 000 kW，然而压缩机实际运行功率为1 149 kW，出现32%误差。基于此，笔者用对比态原理、实际气体Lee-Kesler状态方程、starling状态方程、Soave-Redlish-Kwang (RKS)方程和维里方程等基本状态方程推导出功率计算中关键性的温度绝热指数的求解方法，这不仅可以解决查表法误差大、应用范围小的问题，而且由此可以推出适用更广的功率计算关系式。借助Matlab画出压缩机运行中温度、压缩性系数和绝热指数的变化图，并求解出理论总功率，不仅解决C2，C3类压缩机在功率求解上的空白，而且能形象直观地了解和研究压缩机运行中不同气体、不同工况下各指数的变化关系。

1 绝热指数k的公式推导

经过一系列演算[1]可得出过程指数与气体常数、气体比热、气体压缩性系数、温度的关系式：

(1)

令：

(2)

则式(1)可变为：

(3)

由式(3)可知，要求出温度绝热，就必须先求出压缩性系数Z和X之值。目前求Z值方法有很多，其中Lee-Kesler方程在0.3≤Tr≤4,0≤Pr≤10，范围内可使用,基本满足所有工程实际，尤其适用于非极性和轻微极性气体及其混合物。对 C1到C6的烷烃及乙烯、丙烯、氮、二氧化碳和苯气体的计算，在宽温度和压力范围内其计算出的压缩因子Z的偏差为：过热汽≤0.94%，饱和蒸汽≤1.02%[2]。L-K方程[3]如式(4)所示：

(4)

式中:Z为待求气体的压缩性系数；Z0为简单流体的压缩性系数；ZR为参考流体的压缩性系数；ω为待求气体的偏心因子；ωR为参考流体的偏心因子。简单流体是指Ar等球形结构分子的气体，参考流体用正辛烷(C8H18)，其ωR=0.397 8。

在一定温度和压强下，ZR和Z0可以通过维里方程迭代求得，如下：

(5)

(6)

(7)

(8)

通过查表可查出实际待求气体的偏心因子ω，由于Z计算十分复杂，笔者采用迭代解法，为了表述方便，不妨将该气体在某一温度T、压强P下压缩性系数Z的迭代解设为Z(T,P)，当T，P已知时其为一确定值。

由式(2)可知，要求X，必须得到一个实际气体Z与T的关系式，笔者采用对轻烃类适用性强、精度高的RKS状态方程进行X的计算。RKS状态方程[4]为：

(9)

(10)

(11)

(12)

m=f(w)=0.480+1.57w-0.176w2(13)

其中,Ωa=0.427 48,Ωb=0.086 64。

基本实际气体状态方程为：

Pv=ZRT

(14)

(15)

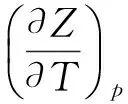
将X，Z代入式(3)即可求出某一温度、压强下的温度绝热指数：

(16)

2 功率公式推导

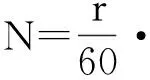
图1 压缩机工作时实际循环图

要精确地表示出绝热指数随时间的变化关系是极其困难甚至是不可能的，因为某些实验数据[6]表明，在极其微小的时间段内，绝热指数甚至出现上下波动的情况。但是宏观上看，绝热指数k的变化规律[7]还是可知的，为了画出C2，C3类气体压缩时的ab和cd段实际变化曲线，笔者作出以下假定：在一极小段的压强变化内气体的绝热指数是不变的，以此求解出功率p。即当n无穷大时，p～p+p/n的压强变化范围内，绝热指数k是不变的。

已知进气压力为Ps，排气压力为Pd，将压强变化分为相等的n个区间，假定每个压力区间内绝热指数是不变的，则每个区间的压力变化量为：

(17)

那么第i个区间的起始点压力为:

Pi=Ps+(i-1)ΔP

(18)

当i=1时，即起始点处，此时P1=Ps，T1=Ts，则第一个区间的绝热指数k1可按式(16)求出：

(19)

已知温度变化公式为：

(20)

第一个区间结束处温度即为第二个区间起始温度，即：

(21)

则第二个区间的绝热指数为：

(22)

通过每个区间起始点压力算出每个区间起始温度，然后依次算出每个区间的绝热指数:

(23)

(24)

对于每个区间，再根据式(25)和第一个区间起始点体积V1，可以依次算出每个区间的起始点体积Vi,如式(26)所示。

Pi-1Vi-1ki-1=PiViki-1=const

(25)

(26)

已知每个区间起始点压强和体积，根据式(25)可以把每一个区间在压缩机工作时的P-V循环图表示出来，这样就可以画出n个小段连接出来的ab曲线，同理可以画出cd曲线，然后通过Matlab就可以计算出abcd包围的面积，从而求解出总功率。

3 Matlab编程求解

由上述压缩因子Z、过程量X和总功率N的求法可知，其计算量很大，且部分运用到数值分析、多元隐函数，必须借助计算机来进行计算。Matlab是一套高性能的数值计算和可视化软件，因此笔者采取Matlab编程来进行求解和仿真验算，简化的计算流程图如图2所示。

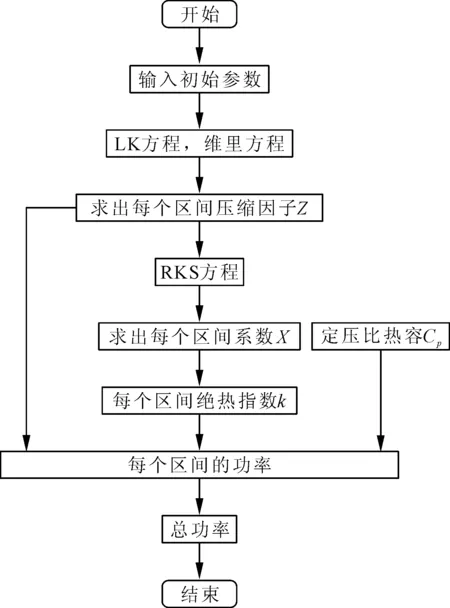
图2 简化的计算流程图

以乙烯压缩机进行验算，乙烯压缩机全负荷状态下的基本数据如表1所示。

传统功率计算式[8]为：

表1 乙烯压缩机全负荷状态下的基本数据

(27)

运行程序，输入初始参数，压强等分数n取100时运行结果如图3所示。程序计算的功率值N=1 072 917.207,即算出的设计功率约为1 073 kW，与1 149 kW的误差只有6.6%，可见笔者提出的功率求解公式相比于传统计算公式精确度提高了很多。但n取值较大时，程序运行时间较长。当n=100时，运行时间已超过1 min。

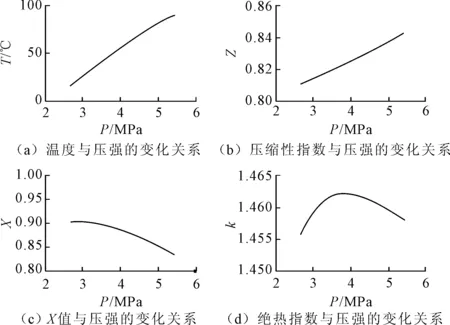
图3 乙烯各参数变化图

由于总功率是由各小区间功率相加得到，需要求n次积分，其计算量大，故笔者利用Matlab对折线ab进行拟合，得到一条光滑曲线，那么只需求一次积分即可求出总功率。修改程序后再次运行，得运行结果N=1 072 917.497，并仿真出循环示意图，如图4所示。其中ab、cd表示拟合后的曲线，可见拟合后的功率基本没变，且大大缩短运算周期。

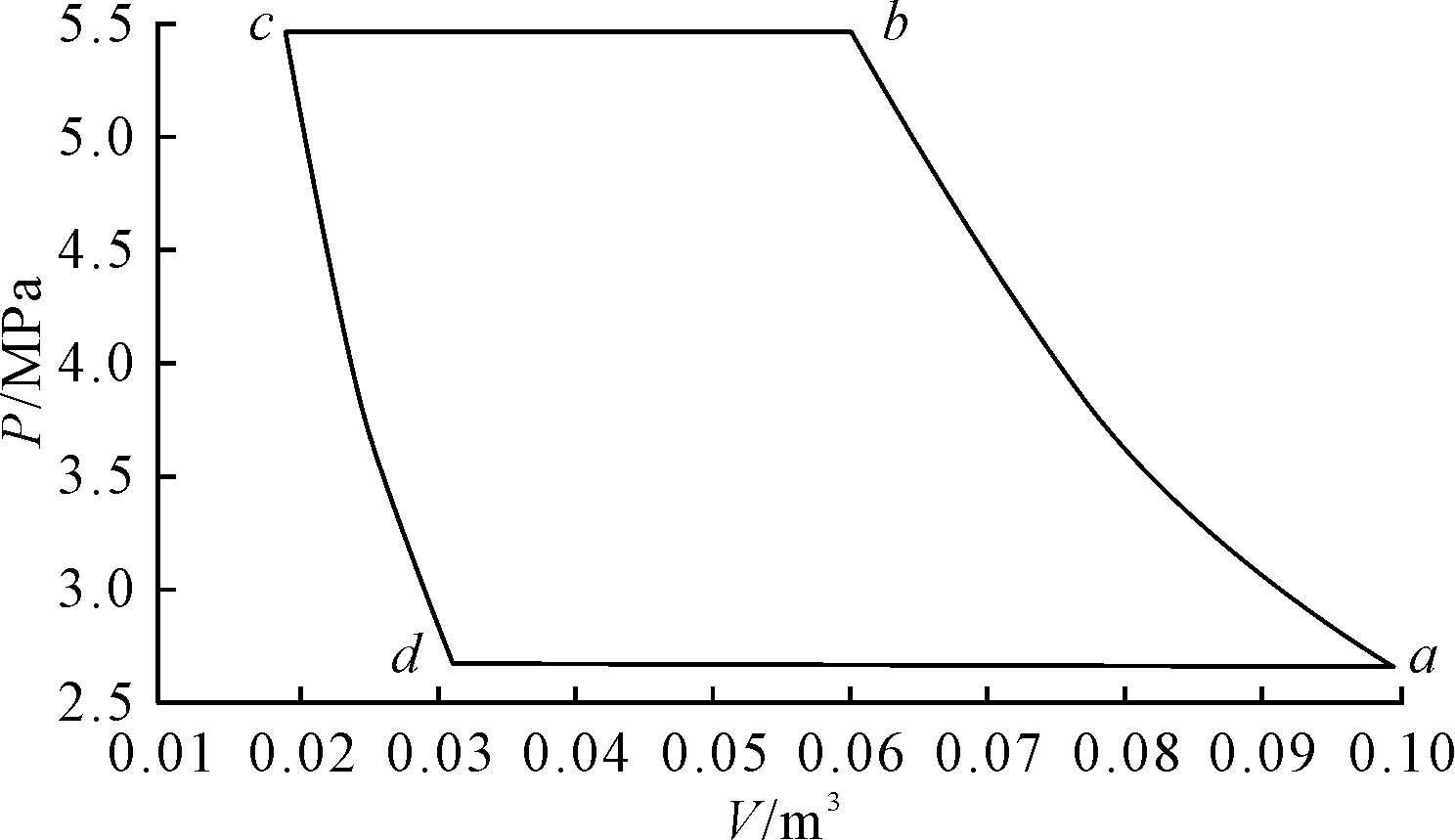
图4 乙烯压缩循环示意图

由式(9)～式(15)可知，临界参数、对比态参数(Tr，Pr)对X有着决定影响，乙烯压缩机运行时恰好是在乙烯的临界温度和临界压强附近工作，X值会大于0，从而导致绝热指数k比零度时的绝热指数要大，最终导致实际功率比按传统功率计算的设计功率要大[9]。

为了验证笔者所提功率求解方法的正确性，把同是临界参数附近工作的C2、C3类气体(如乙烷)带入程序，输入相同的初始参数运行，得到图5所示乙烷参数变化图和图6所示功率计算指示图，功率N=1 075 719.662，而按传统功率计算公式计算出的功率约为850 kW，可以得到与前所述相同的结论。

图5 乙烷各参数变化图

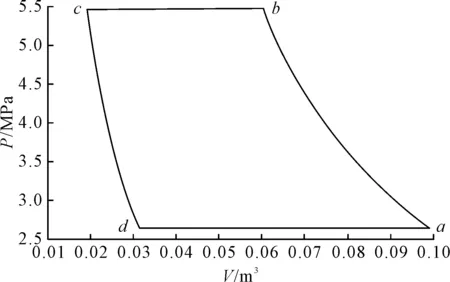
图6 乙烷功率计算指示图

通过公式推导可知，笔者所提功率公式也适用非C2,C3类气体，以氮气、氢气为例，假定入口温度为20 ℃，入口压强为2.5 MPa，出口压强为5.0 MPa，用传统公式计算的功率和笔者方法解出的指示功率如表2所示。

由表2可知，对于介质不在临界参数附近工作的压缩机，笔者方法解出的功率与传统功率解相对误差的绝对值不到1%，可见笔者所提出的功率求解法更具普适性。同时氢气和氮气各参数变化也完全符合实际情况，如图7和图8所示。

表2 传统公式与笔者方法解出指示功率对比

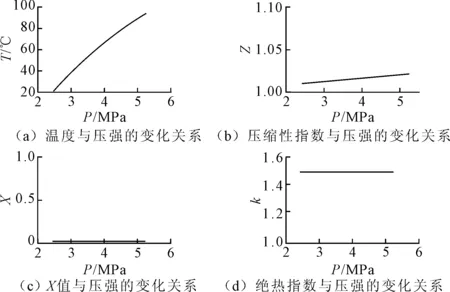
图7 氢气各参数变化图

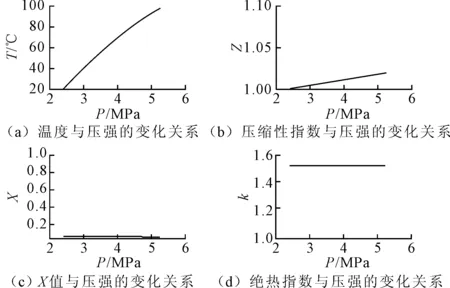
图8 氮气各参数变化图

4 结论

传统功率计算认定气体的绝热指数是不变的，如氢气、氮气、空气等非C2，C3类气体取0 ℃测得的绝热指数计算功率的误差较小[10]，但传统功率公式并不适合所有气体，C2，C3类气体压缩机在临界参数附近工作时，工作温度和压强皆在临界参数附近，当工作温度高于0 ℃时，绝热指数较传统公式在0 ℃测得的绝热指数会大很多，而且有一定的波动，仍以0 ℃时的绝热指数来进行计算，会导致设计功率偏小。笔者推导出的功率解法，并不只适用于C2，C3类气体，而是对所有气体都适用。不仅能很较地解决传统功率公式不适合C2、C3类压缩机的难题，而且可以避免传统公式计算中查图表选取Z、k值的误差，其精度也比传统功率计算公式高。

[1] 郁永章.活塞式压缩机[M].北京：机械工业出版社,1982：12-57.

[2] 李珍华，缪玲梅.实际气体压缩因子的应用[J].上海化工,2014，39(3)：7-10.

[3] 苏洛养.三参数法求气体压缩性系数的计算机解[J].压缩机技术,1990,100(2)：21-25.

[4] 王东宇,李岳,王淑兰.R-K-S方程在压缩因子计算中的应用[J].化学工业与工程技术,2001,22(5)：32-36.

[5] 林梅,孙嗣莹.活塞式压缩机原理[M].北京：机械工业出版社,1987:16-34.

[6] 张勇，陈浩，杨金.天然气压缩机多变过程指数的研究[J].机械,2008，35(1):27-33.

[7] 王君,李强,李娟娟.往复压缩机气体压缩热力过程研究[J].流体机械,2008(1)：22-25.

[8] 活塞式压缩机编写组.活塞式压缩机设计[M].北京：机械工业出版社,1974：22-53.

[9] 石玉美，孙嗣莹.超高压乙烯的热力学参数计算[J].流体机械,1994(11):22-29.

[10] 冯全科.往复式压缩机指示功率计算公式的精度分析[J].压缩机技术,1989，95(3)：13-15.

SHEN Shuncheng:Assoc. Prof.; School of Mechanical and Electric Engineering, WUT, Wuhan 430070, China.

[编辑：王志全]

C2and C3Gas Compressor Power Solution Based on Matlab

SHENShuncheng,HEBo,LIZhangjie

In consideration of that the traditional power calculation is not suitable for the C2，C3 compressor near the critical parameters problems, we introduced a formula of adiabatic index k and a more general power calculation formula through a series of real gas state equation and the theorem of corresponding states. And the power of C2 C3 compressor can be successfully solved out by the Matlab calculation program.

C2C3compressor; adiabatic index; Matlab; power solution

2015-07-02.

沈顺成(1959-)，男，湖北武汉人，武汉理工大学机电工程学院副教授.

武汉高新技术开发基金资助项目(2014010101010010).

2095-3852(2015)06-0832-05

A

TH457

10.3963/j.issn.2095-3852.2015.06.037