基于压缩感知的稀疏重构DOA估计算法
2015-02-16包晓蕾曲行根王卓英
包晓蕾,曲行根,王卓英
(1.上海电子信息职业技术学院 通信与信息工程系,上海 201411;2.哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
基于压缩感知的稀疏重构DOA估计算法
包晓蕾1,曲行根2,王卓英1
(1.上海电子信息职业技术学院 通信与信息工程系,上海 201411;2.哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
基于空间目标分布的稀疏特性和压缩感知理论思想,提出一种基于奇异值分解的多测量梯度投影稀疏重构(SVD-MGPSR)算法,将多目标DOA估计转化为一个稀疏信号重构问题。首先利用阵列流形建立的过完备原子库对信号进行联合稀疏表示,然后对压缩采样后的信息矩阵进行奇异值分解,可以明显降低运算量,最后基于MGPSR算法对稀疏信号进行重构,从而实现DOA估计。相对于已有算法,该算法不仅在低信噪比、小快拍数条件下测向均方误差较小,而且能够对相干信号进行正确估计,具有较高的测向精度和角度分辨率。仿真实验验证了该算法的有效性。
压缩感知;DOA估计;奇异值分解;梯度投影
目标信号波达方向(direction of arrival, DOA)估计一直是阵列信号处理领域中的一个重要研究方向,在通信、雷达和医学成像等领域有着广泛的应用[1]。目前,国内外学者已经提出了大量有效的DOA估计算法,其主要分为两大类:一类是基于波束形成的测向方法,如由BURG提出的最大熵谱估计法(maximum entropy spectral estimation method, MEM)[2]和CAPON提出的最小方差无失真响应估计法(minimum variance distortion response, MVDR)[3]等;另一类基于子空间的测向方法,如由SCHIMIDT提出的多重信号分类(multiple signal classification, MUSIC)算法[4]和ROY等提出的旋转不变子空间(estimation of signal parameters via rotational invariance techniques, ESPRIT)算法[5]等。然而,基于波束形成的算法虽然克服了阵列孔径限制,但估计分辨率不高且受噪声影响较大;基于子空间的算法具有高分辨率,但对于相干信号由于信号协方差矩阵会出现失秩现象,故无法有效估计。
近几年一种新颖的压缩感知(compressing sensing, CS)[6]理论已广泛应用于图像分析、信号处理等领域,受到了学者们极大关注。CS理论是指可以用远低于奈奎斯特采样定理要求的采样速率对可压缩或可稀疏信号进行非自适应采样,然后通过求解凸优化问题恢复信号。
由于可以将空间进行网格划分并且实际目标角度仅占较少单元,故目标在空间域是稀疏的。基于上述思想,可以将压缩感知应用到DOA估计中[7-8],文献[9]提出一种利用混合l2,0范数(JLZA-DOA)优化算法来近似求解联合稀疏问题,从而对信号进行DOA估计。文献[10]采用梯度投影稀疏重构(gradient projection for sparse reconstruction, GPSR)算法重构信号,该算法梯度约束条件过于严格并且只适应于单快拍系统,在低信噪比条件下均方误差较大。针对上述问题,笔者提出一种新的基于奇异值分解(singular value decomposition, SVD)的多测量梯度投影稀疏重构(SVD-MGPSR)算法。该算法首先基于阵列流型矩阵建立的过完备原子库构造稀疏基矩阵,构造稀疏信号模型,采用满足约束等容条件(restricted isometry property, RIP)[11]的随机矩阵进行时域压缩采样,然后对压缩采样后的信息矩阵进行奇异值分解,最后采用新算法重构稀疏信号矩阵,完成DOA估计。笔者采用的奇异值分解方法进行信号降维处理可以得到低维信号子空间,运算量明显降低并且能够提高抗噪声能力。与已有的MUSIC算法、MVDR算法和文献[9]中提到的JLZA-DOA算法相比,该算法不仅能够对相干信号正确测向,而且在低信噪比、小快拍数条件下测向均方误差较小,具有较高的角度分辨力及更优的测向性能。
1 压缩感知
CS理论原理:信号若是可压缩性的或稀疏性的,可以通过与变换基不相关的测量矩阵将高维信号投影到低维信号上,再求解凸优化问题,从少量投影值中重构原始信号。其由3个核心部分构成:信号稀疏表示、测量矩阵的设计和信号重构算法[12]。
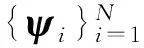
(1)
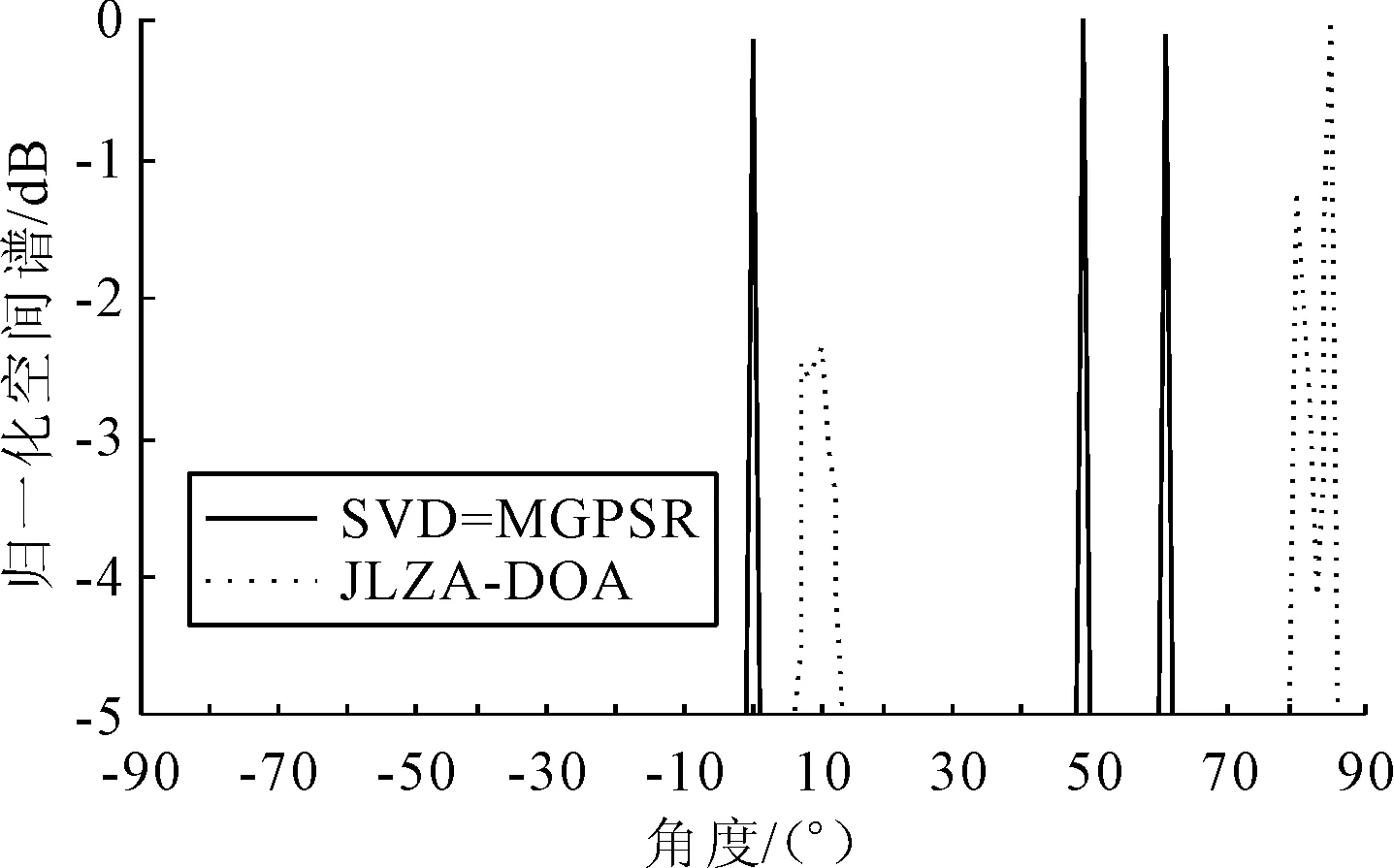
其中,α=[α1,α2,…,αN]T是信号x在正交基矩阵Ψ的表示系数,因此α和x是信号的等价表示。若系数矢量α只含有K(K 在CS理论中,信号稀疏表示之后,将信号压缩投影到M×N的测量矩阵Φ上得到投影值y=[y(1),y(2),…,y(M)]T,其中M y=Φx=ΦΨα=Θα (2) 其中,Θ=ΦΨ是M×N的感知矩阵,也称之为CS的信息算子[13]。CS理论的关键部分就是从这M个投影值中重构出长度为N的稀疏信号或信号的系数矢量。求解式(2)是一个欠定问题,一般来讲无确定解,但研究表明:对于一个稀疏信号,当Θ满足RIP条件时可以通过求解l0范数问题精确重构原始信号: ‖α‖l0s.t.y=Θα (3) ‖α‖l1s.t.y=Θα (4) 2.1 接收信号模型 设各向同性的N个阵元构成一个均匀线阵,有K个远场信号sk(t),k=1,2,…,K分别以方向θi,i=1,2,…,K入射到该线阵,则第n个阵元接收信号为: n=1,2,…,N (5) 式中:nn(t)为第i个信号在t时刻的噪声;τni为第i个信号到达第n个阵元相对于参考阵元的时延;gni为第n个阵元对第i个信号的增益。各阵元是同向的,并且阵元之间不考虑通道不一致性、互耦等因素,阵元增益可以归一化为1。这里令第一个阵元为参考阵元,则相对于参考阵元的延时可以描述为τni=(n-1)dsin(θi)/c,式中d为均匀线阵阵元间隔。假设阵元接收到的是中心频率为ω0的窄带信号,则第n个阵元接收信号为: nn(t) n=1,2,…,N (6) 将式(6)写成矢量形式如下: X(t)=AS(t)+N(t) (7) 式中:X(t)=[x1(t),x2(t),…,xN(t)]T为N维接收数据矢量;S(t)=[s1(t),s2(t),…,sK(t)]T为K维信号矢量;N(t)=[n1(t),n2(t),…,nN(t)]T为N维噪声矢量;A=[a(θ1),a(θ2),…,a(θK)]为N×K维阵列流型矩阵。 2.2 过完备原子库建立 根据阵列流形结构建立过完备原子库。原子库结构需要尽可能地逼近信号结构,并能用尽可能少的原子最佳线性表示信号,由此可建立如式(8)所示的过完备原子库的原子: i=1,2,…,P (8) X=ΨZ+N (9) 其中,Z为信号S在原子库的稀疏系数矩阵。 2.3 联合稀疏模型 系统快拍数为L,第i次快拍数接收的信息矢量为yi,稀疏系数矢量为zi,噪声矢量为ni,且满足均值为零方差为σ2的复正态分布,根据CS理论可得: Y=ΦX=ΦΨZ+ΦN=ΘZ+ΦN (10) 3.1 联合稀疏模型SVD处理 针对降低运算量和复杂度的要求,基于子空间思想对接收到的信息矩阵进行SVD降维处理,提取信号子空间。传统的子空间算法对协方差矩阵进行特征分解时要求信号不相关,当信号相关时,协方差矩阵会出现损秩,降低测向性能。笔者在不要求信号是否相关的条件下,对式(10)的信息矩阵进行降维处理: Y=UΣVH=[USUN]Σ[VSVN]H (11) 式中:U和V是正交矩阵;矩阵Σ对角线元素按照由大到小排列,即σ1≥σ2≥…≥σK≥σK+1≥…≥σM。信号子空间矩阵US由K个大奇异值对应的左奇异向量组成,而噪声子空间UN由其余M-K个小奇异值对应的左奇异值向量组成。在信源数已知的条件下进一步推导可得M×K维的信号子空间US=YS=UΣΒK=YVΒK,其中,ΒK=[IK0]H,IK为K×K维单位矩阵,0为K×(L-K)维零矩阵。同时可得ZS=ZΣΒK,NS=NΣΒK,由此代入式(11)可得降维表示式: YS=ΘZS+ΦΝS (12) 由式(12)可知,通过SVD处理信息,矩阵由M×L维降为M×K维,尤其在大快拍数条件下,求解式(12)可以显著降低运算时间,并且由初等列变换得到的ZS与系数矩阵Z具有相同的稀疏特性,故求解式(12)是具有可行性的。另外,从上述分析可知,SVD分解实质是一个信号分量累积的过程,使得在低信噪比的条件下也具有较好的估计性能。 3.2 SVD-MGPSR算法 传统的GPSR算法是利用拉格朗日乘法将式(4)改写成如下无约束凸优化问题: (13) 其中,τ(>0)称为拉格朗日因子或者正则因子。引入正则因子的目的是在抑制噪声干扰和稀疏特性上有效均衡。目标函数中l2范数项表征重构信号与原始信号能量差值,来抑制噪声的影响,而l1范数项表征重构信号的稀疏度。通过将zS中的值分为同维数的正部分u和负部分v,即ui=(zSi)+、vi=(-zSi)+,i=1,2,…,N,可以把式(13)转化成标准的边界约束二次规划(bound-constrained quadratic programming, BCQP)问题: 首先,SVD-MGPSR算法的目标函数如式(15)所示: (15) (16) (17) 根据矩阵求迹运算性质可将式(17)进一步化简为: (18) (19) (20) 笔者仿真针对远场窄带信号模型,与已有的MUSIC算法、MVDR算法和JLZA-DOA算法进行比较,来验证笔者SVD-MGPSR算法的性能。仿真中,空间信号随机采样均采用16个阵元的均匀线阵,阵元间距为半波长,信号幅度服从零均值、方差为1的复高斯变量,且与复高斯白噪声互不相关。SVD-MGPSR算法中测量矩阵采用随机高斯矩阵,且参量τ定义为: 利用均方根误差作为估计的性能指标,DOA估计均方根误差定义为: 实验1 假设空间3个非相干信号分别以θ1=0°、θ2=49°和θ3=61°方向入射,信噪比为3 dB,快拍数L=100,比较SVD-MGPSR算法与其他3种算法的归一化空间谱。图1给出了4种算法的归一化空间谱图,从图1中可以看出:SVD-MGPSR算法比其他3种算法具有较窄的主瓣宽度和较低的旁瓣,其空间谱类似于针状,具有较高的角度分辨率,且旁瓣没有波动现象,噪声对新算法测向性能影响较小。 图1 非相干信号空间谱 实验2 假设空间入射角度分别为θ1=49°和θ2=61°的两个非相干信号。图2为各算法在快拍数L=100和信噪比SNR=-5 dB:10 dB条件下,每个信噪比做50次蒙特卡洛实验时DOA估计均方根误差变化情况;图3为在SNR=15 dB和快拍数L=25:5:50情况下,每个快拍数做50次蒙特卡洛实验时4种算法的均方根误差变化情况。从图2和图3可以看出:在低信噪比、小快拍数条件下SVD-MGPSR算法和JLZA-DOA算法的均方根误差明显小于MUSIC算法和MVDR算法,具有较高的测向精度,能够保证在低信噪比、小快拍数条件下的测向性能;当信噪比足够高、快拍数足够大时各算法均方根误差相差不大具有相近的测向性能。 实验3 考虑空间3个相干信号,入射角度分别为θ1=0°、θ2=49°和θ3=61°,信噪比为3 dB,快拍数L=100,由于MUSIC算法和MVDR算法对相干信号失效,故只比较JLZA-DOA算法和SVD-MGPSR算法对相干信号的测向能力,图4给出了相干信号时两种算法的归一化空间谱图,从图4可以看出,JLZA-DOA算法对于相干信号不能正确测向,而SVD-MGPSR算法能够较强地分辨信号且信号相干性对测向影响不大,表现出对相干信号具有较强的DOA估计能力。 图2 均方根误差随信噪比变化曲线 图3 均方根误差随快拍数变化曲线 图4 相干信号空间谱 笔者在压缩感知框架下建立了联合稀疏信号模型,采用奇异值分解进行信号降维处理能明显降低计算量;与已有算法相比,新算法不仅能在低信噪比、小快拍数条件下完成高精度估计,而且也可以对任意相干信号进行有效估计,具有较高的测向精度和角度分辨率。 [1] DAI J S, XU W C, ZHAO D A. Real-valued DOA estimation for uniform linear array with unknown mutual coupling[J]. IEEE Trans on Signal Processing, 2012,92(9):2056-2065. [2] BURG J P. Maximum entropy special analysis [C]∥Proc of the 37th Meeting of the Society of Exploration Geophsicists.[S.l.]:[s.n.],1967:1213-1213. [3] CAPON J. High-resolution frequency-wave number spectrum analysis [J].Proc IEEE, 1969,57(8):1408-1418. [4] SCHIMIDT R O. A signal subspace approach to multiple emitter location and spectrum estimation [D]. Stanford: Stanford University, 1981. [5] ROY R,KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques [J]. IEEE Trans on Acoustics Speech and Signal, 1986,37(7):984-995. [6] DONOHO D L. Compressed sensing [J]. IEEE Trans on Information Theory, 2006,52(4):1289-1306. [7] YANG Z, XIE L H, ZHANG C S. Off-grid direction of arrival estimation using sparse bayesian inference [J]. IEEE Trans on Signal Processing, 2013,61(1):38-43. [8] 贺亚鹏,李洪涛,王克让,等.基于压缩感知的高分辨DOA估计[J].宇航学报,2011,32(6):1344-1349. [9] MD M H, KAUSHIK M. Direction-of-arrival estimation using a mixedl2,0norm approximation [J]. IEEE Trans on Signal Processing, 2010,58(9):4646-4655. [10] FIGUEIREDO A T, ROBERT R D, WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems [J]. IEEE Journal of Selected Topics in Signal Processing, 2007,1(4):586-597. [11] STROHMER T. Measure what should be measured: progress and challenge in compressive sensing[J]. IEEE Trans on Signal Processing Letters, 2012,19(12):887-893. [12] 林波.基于压缩感知的辐射源DOA估计[D].长沙:国防科技大学,2010. [13] 石光明,刘丹华,高大化.压缩感知回顾与展望[J].电子学报,2009,37(5):1070-1081. [14] SHISHKIN S L. Fast and robust compressive sensing method using mixed hadamard sensing matrix [J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2012,2(3):353-361. [15] BARZILAI J, BORWEIN J. Two point step size gradient methods [J]. IMA Journal of Numerical Analysis, 1988,8(1):141-148. BAO Xiaolei:Lect.; School of Communication and Information, Shanghai Technical Institute of Electronics & Information, Shanghai 201411, China. [编辑:王志全] Sparse Reconstruction DOA Estimation Algorithm Based on Compressive Sensing Theory BAOXiaolei,QUXinggen,WANGZhuoying Based on the sparse property of the spatial targets distribution and the idea of compressive sensing (CS) theory, a multi-measurement gradient projection for sparse reconstruction algorithm based on singular value decomposition (SVD) was proposed, in which a multi-targets DOA estimation problem can be translated into a sparse signal reconstruction problem. Firstly, the signal was joint sparse representation by establishing an over-complete atom dictionary according to array manifold matrix. Then, SVD of information matrix of compressive sampling was done to reduce the amount of computation greatly. Finally, the sparse signal was reconstructed based on multi-measurement vectors gradient projection for sparse signal reconstruction algorithm so as to achieve DOA estimation. Compared with existing algorithm, the proposed algorithm not only has a smaller mean square error in the low SNR but also is able to correctly estimate the coherent signal. Moreover, it offers higher direction finding precision and angular resolution. The simulation results verify its effectiveness. compressive sensing; DOA estimation; SVD; gradient projection 2015-08-25. 包晓蕾(1981-),女,山东烟台人,上海电子信息职业技术学院通信与信息工程系讲师. 上海市教育委员会教育发展基金资助项目(09CGB06). 2095-3852(2015)06-0827-05 A TN911 10.3963/j.issn.2095-3852.2015.06.036

2 基于CS理论的信号模型
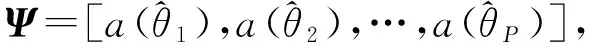
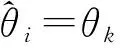
3 信号重构算法
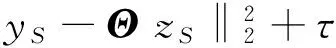
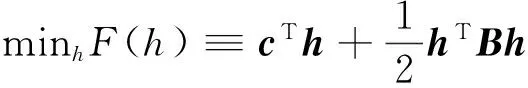
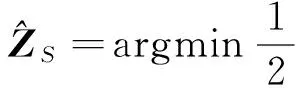
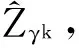

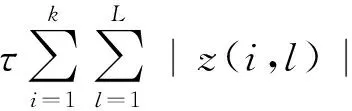
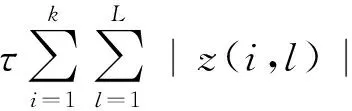
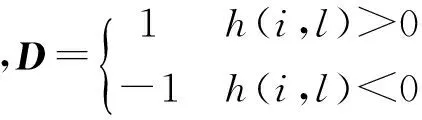
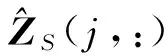
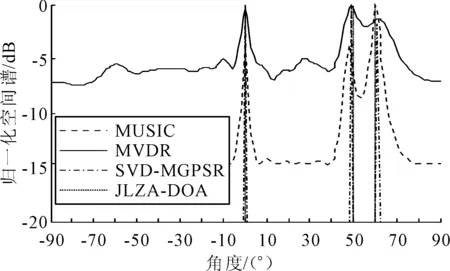
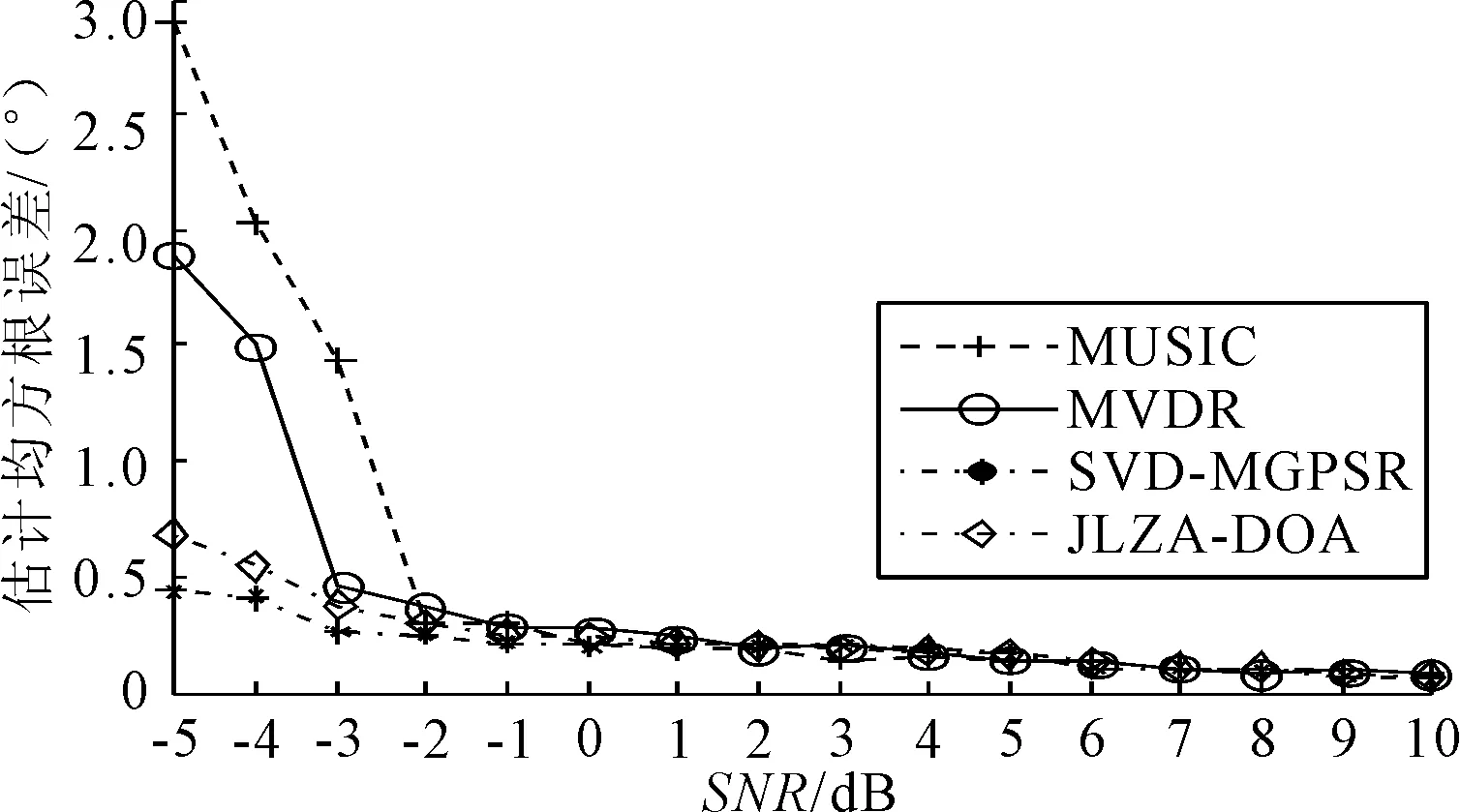
4 仿真分析
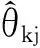
5 结论
