基于集对分析与NSGA-II的工程项目多目标优化

翟 瑞，张云宁，陈国伟，赵迎亮

(1.河海大学 商学院，江苏 南京 211100；2.江苏省电力设计院有限公司，江苏 南京 210000；3.南京城建集团，江苏 南京 210000)



基于集对分析与NSGA-II的工程项目多目标优化

翟 瑞1，张云宁1，陈国伟2，赵迎亮3

(1.河海大学 商学院，江苏 南京 211100；2.江苏省电力设计院有限公司，江苏 南京 210000；3.南京城建集团，江苏 南京 210000)

工程项目进度、成本和质量三者是对立统一的，工程项目的多目标优化着重于求解三者的和谐统一。以工程项目施工过程中的进度、成本和质量水平阈值为约束条件，运用集对分析法为建筑工程多目标优化问题的处理构建了柔性的建模框架;利用NSGA-II算法求解多目标优化模型，得到多目标优化的Pareto最优解集;通过实际算例验证了该算法在解决工程项目多目标优化问题中的可行性和有效性。

工程项目;多目标优化；集对分析；Pareto解集；NSGA-II算法

进度、成本和质量是工程项目的三大控制目标，这三大目标不是完全相容的，甚至是相悖的[1]。多目标优化的理想状态是在资源得到均衡充分利用的情况下达到工期最短、成本最低及质量最优。BADU等基于工程的质量水平、持续时间和成本之间呈线性关系的假设，分别针对质量、成本和工期建立了3个线性规划模型来研究三者之间的平衡关系[2]。马超等将风险作为优化目标，建立了优化TCQR多目标模型，并通过MOEA/D算法进行求解[3]。陈勇强等利用Pareto最优原理对工程项目优化调度问题进行求解[4]。

笔者基于集对理论，考虑工程项目施工过程的成本型指标和效益型指标，建立多目标的集对联系度模型，为进度、成本和质量的优化构建柔性建模框架，再运用NSGA-II算法求解多目标的优化模型最优解。

1 基于集对分析的多目标优化模型

集对分析理论(set pair analysis,SPA)最早是在1989年由我国学者赵克勤[5]提出的一种新的系统分析方法，主要是针对系统中的确定、不确定信息从同异反3个方面定量分析两个集合之间的相互联系、影响和转换，并通过联系度μ=a+bi+cj定量地描述集合在研究背景下的同异反联系程度大小。a表示两个集合的同一程度，c表示对立程度，a+c就代表这两个集合的确定度；b表示两个集合的差异度，即系统的不确定度；差异度系数i的取值范围为[-1,1]，对立度系数j按照一定概率取值-1,0或者1。其中a,b,c满足a+b+c=1的归一化条件。

1.1 工程项目多目标集对联系度分析

将工程项目成本目标、进度目标和质量目标分为经济型指标和效益型指标，各资源配置计划的效益也可以具体量化为完成关键作业的经济型水平和效益型水平。

在实际优化过程中，可以选择智能算法或者以往工作经验来确定工程项目的施工作业多目标优化方案，但由于不确定性因素的存在不能使最终的多目标优化达到最优状态，而集对分析法利用联系度可以将确定性和不确定性在同一个系统中进行统一辩证处理，为工程项目多目标优化问题的处理构建柔性的建模框架。

对于经济型指标最劣与最优水平分别记作WU和WV，最低与最高值可以从项目内部或外部根据项目实际目标和客观条件来确定，亦可由式(1)和式(2)确定：

(1)

(2)

式中：M为工程项目所包含的关键作业数量；Nj为参与第j项关键作业的资源配置计划；Fjk为资源配置计划k完成第j项关键作业的成本值。 实际优化方案I的经济指标为：

(3)

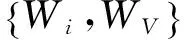
(4)

式中:同一度aWi和对立度bWi表示建筑工程优化方案经济型指标的优劣程度，aWi=S/N,bWi=P/N；差异度cWi表示评价指标的不确定性，cWi=F/N；i是取值范围为[-1,1]的差异度系数;j为对立度系数,一般取-1；N为集对Wi、WV在建筑工程成本、质量、进度多目标优化问题背景下的特性数总和，其中在S个特性上Wi、WV是共同的；有P个是Wi、WV相对立的特性，在F=N-S-P个特性上Wi、WV的关系是不确定的。

与经济型指标相反，效益型指标越大对整体目标优化越有利，设效益型指标最劣与最优水平分别为BU和BV，计算公式为:

(5)

(6)

其中，Bjk为施工班组k完成第j项分类分项工程的效益值。

实际优化方案I的效益指标为:

(7)

则实际方案I的经济成本集对{Bi,BV}联系度为:

(8)

1.2 工程项目多目标优化集对联系度模型

对经济型指标和效益型指标分别进行集对联系度分析之后，以工程质量、进度和成本阈值作为约束条件构建多目标贴合度模型：

(9)

(10)

(11)

s.t.Qi≥Qth

(12)

Ei≥Eth

(13)

Ci≤Cth

(14)

Qth≥0,Eth≥0,Cjk≥0

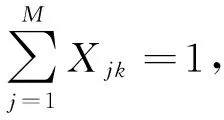
式(9)～式(11)分别为在相对确定条件下的质量、进度和成本的优化目标，即三者的贴合度最大。ΘQi、ΘEi、ΘCi分别为质量贴合度、进度贴合度和成本贴合度；aQi、aEi、aCi分别为质量、进度和成本的同一度程度；cQi、cEi、cCi分别为质量、进度和成本的对立度程度；Qi、Ei、Ci分别为施工过程中的实际施工质量水平、进度和成本，Qi、Ei、Ci必须都满足最低的施工质量可靠性阈值、最低效率阈值和最大预算成本阈值的约束条件。

2 基于NSGA-II的建筑工程多目标优化

2.1 NSGA-II算法

在建立了工程项目多目标优化模型之后，为了提高优化系统的鲁棒性，需要采用有效的算法来寻求在该研究背景下的最优方案集。

SRINIVAS和DEB在1995年提出了非支配排序遗传算法(nondominated sorting genetic algorithms，NSGA)[7]，NSGA优点在于利用非支配分类程序将多目标简化成一个适应度的函数。

2000年印度科学家在此基础上提出了改进的快速非支配排序遗传算法NSGA-II[8]，定义了拥挤距离概念来对某个点周围的解密度进行估计，采用拥挤距离比较算子来代替复杂的参数适值共享方法。

笔者通过NSGA-II算法来实现工程项目多目标贴合度的优化，寻找在该特定问题背景下同一度大、对立度小的最佳方案集。NSGA-II算法的优化过程是根据工程项目施工指标和各资源配置计划的施工标准数据得到工程项目质量、成本和进度参数的阈值范围，再以不同资源配置计划行程的活动模式为决策变量，在给定的约束阈值条件下，实现施工的质量、成本和进度指标的多目标优化。

2.2 NSGA-II算法基本流程

NSGA-II算法依据小生境密度比较算子使得Pareto元素扩展到整个Pareto域中，使种群的多样性得到保证；同时引进精英政策，扩大了采样空间，也使整个系统的效率和鲁棒性得到提高。带精英策略的NSGA-II算法流程图如图1所示。

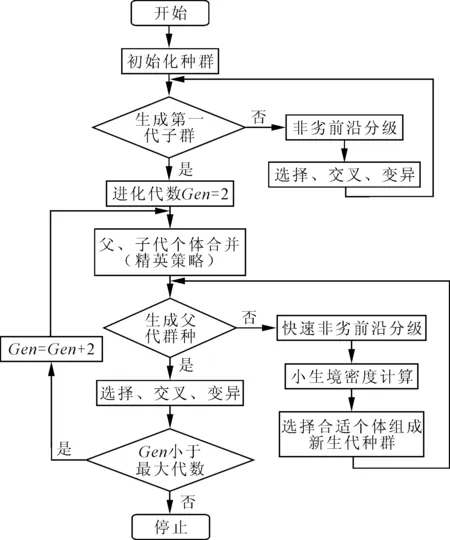
图1 NSGA-II算法流程图

(1)种群初始化，随机生成规模为N的初始种群。

(2)非劣前沿分级后进行选择、交叉和变异之后生成第一代子代种群。

(3)对合并后的二代父、子代种群进行快速非劣前沿分级。

(4)对非劣前沿分级层结果中的个体进行小生境密度计算，再依据小生境密度和非劣前沿关系选取适合的个体组成新的父代种群。

(5)对新生成的父代种群进行选择、交叉和变异操作生成新的子代种群。

(6)重复步骤(3)～步骤(5)，直到达到预先设定的迭代次数，即可获得多目标优化问题的Pareto最优解集。

3 算例分析

为验证集对分析与NSGA-II算法相结合对建筑工程多目标优化的资源配置问题解决的有效性和可行性，对某个实际大桥的主墩群桩基施工过程进行分析研究。主墩群桩基施工GERT的随机网络模型如图2所示。

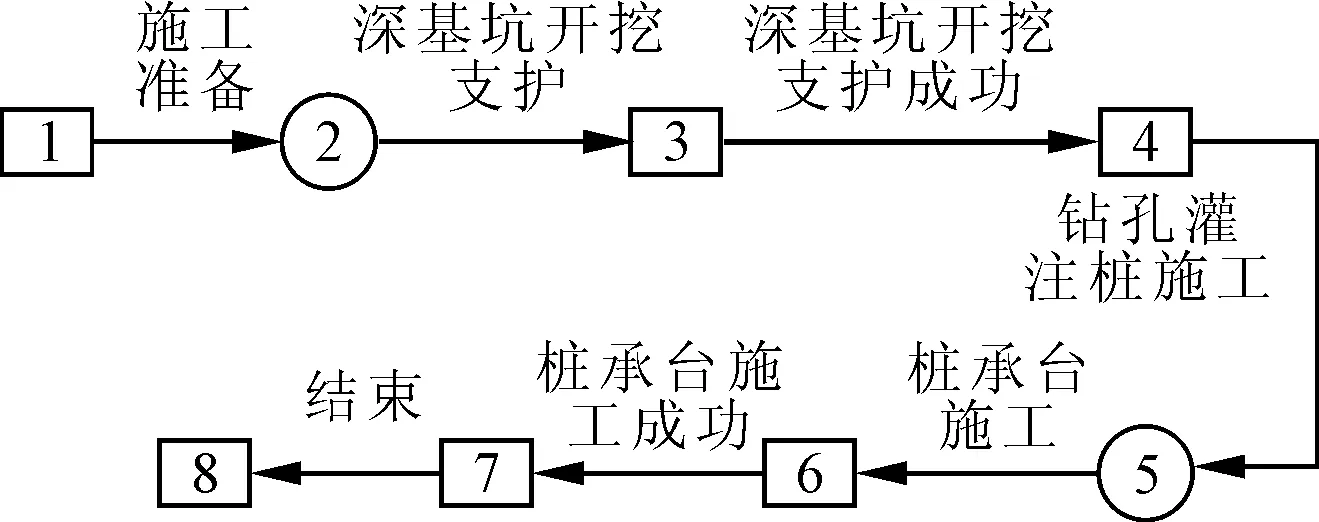
图2 主墩群桩基施工GERT的随机网络模型

根据主墩群桩预先拟定的施工方案、进度计划和预估成本，在对施工现场实际情况进行分析的基础上，采用专家调查法对该工程的工期和费用各参数进行估计，数据如表1所示。

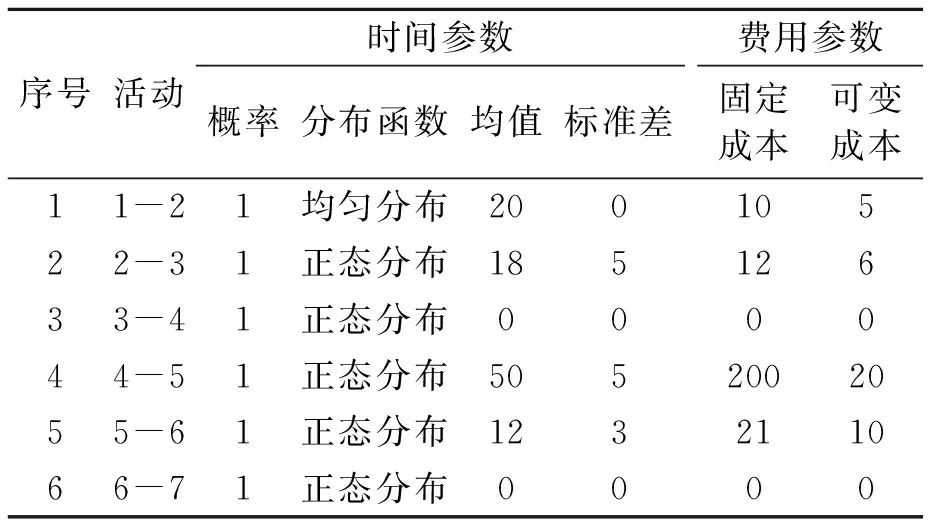
表1 关键作业时间和费用参数估计表

利用水晶球软件对主墩群桩基总工期和总费用进行模拟分析,计算结果如表2所示。由于主墩群桩基施工的各项工作是相互独立的，可先求出各单项工作的局部优化，进而合并优化子集以求得全局最优解集。在运用NSGA-II算法对施工作业进行优化调度时，需对经济型指标和效益型指标分别设置上、下限约束以确保多目标优化的准确性及优化结果的合理性。主墩群桩基施工各项活动的质量、进度和成本参数约束范围如表3所示。

表2 各活动节点工期及费用模拟值

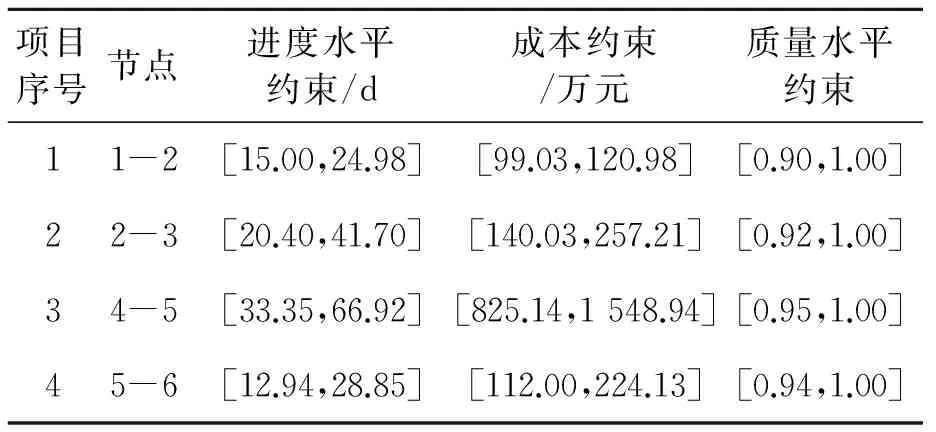
表3 主墩群桩基施工各项活动参数范围

工程项目中各活动因为资源配置方案的差异而形成不同的活动模式，从而产生不同的目标效果。算例中的决策变量为活动模式，用mi表示活动i的模式数量为m个，多目标优化需要从活动i的mi个模式中选择一个j(j=1,2,…,mi)作为决策变量，使得最终的资源配置方案能够使目标优化的目标方程最优，即达到质量、进度和成本的贴合度最高。各资源配置使用模式量化后相对应的质量水平、进度水平和单位成本如表4所示。

针对多目标优化模型和算例数据，利用Matlab7.0软件进行NSGA-II算法的实现，求得各活动模式的非支配最优解组合,如表5所示。

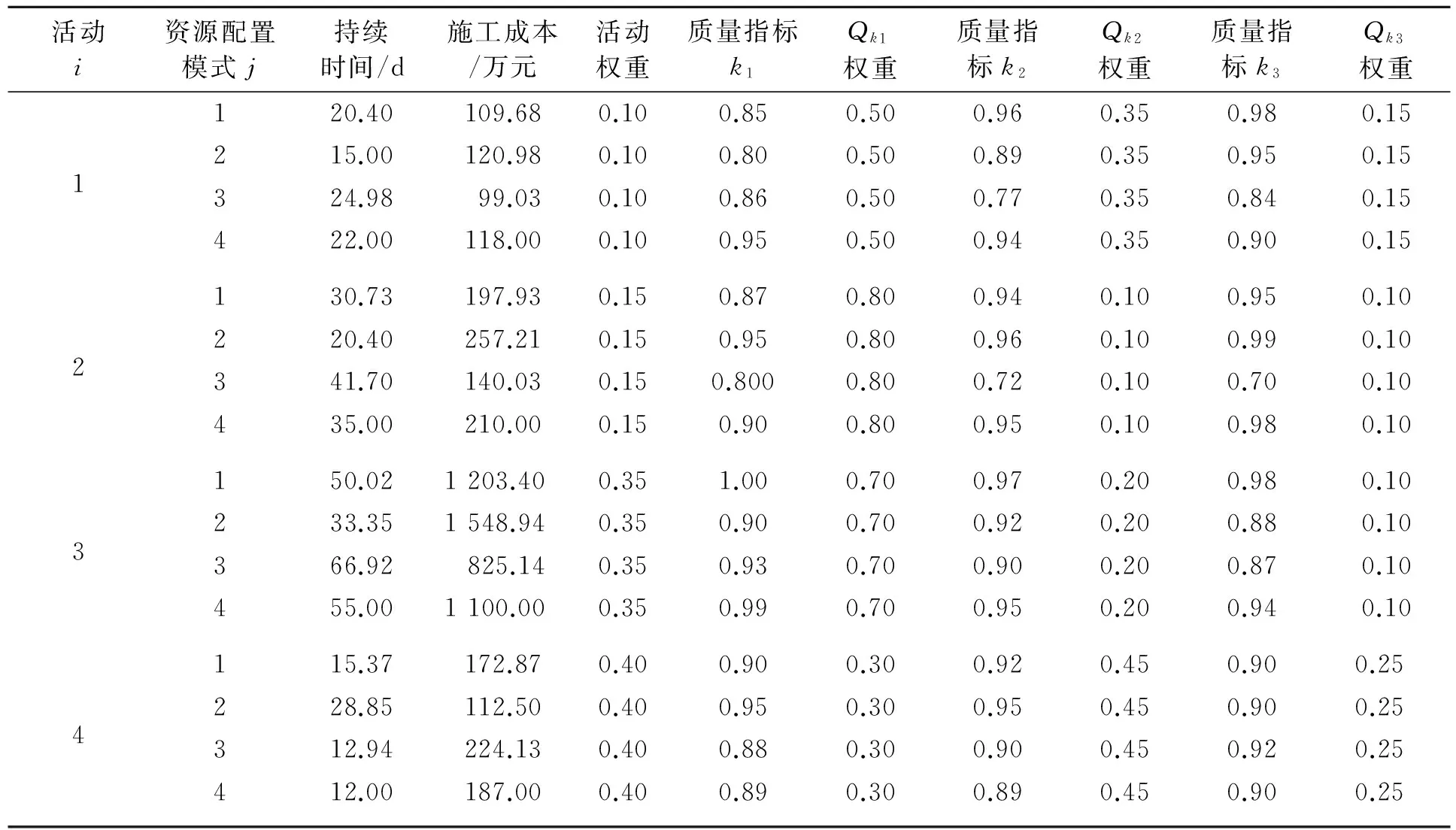
表4 各资源配置使用模式参数数据

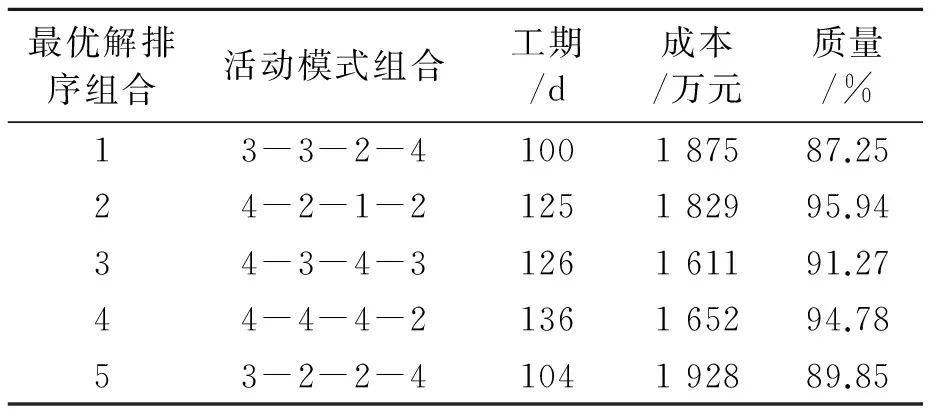
表5 多目标优化非支配最优解组合

表5给出了主墩群桩基施工的5组最优解组合，与传统的遗传算法如粒子群和蚁群算法等相比，NSGA-II算法克服了多目标优化方案解的唯一性，管理者可以根据实际施工过程中的具体要求选择不同的资源配置模式。在资源配置计划调度问题研究中，NSGA-II算法中的遗传操作参数对最终的计算结果影响很小，相比其他传统算法具有较高的鲁棒性。种群规模及进化代数参数设置可根据具体问题进行从小到大的逐步调整，得到的结果具有稳定、足够多且分布均匀的Pareto解集前端，NSGA-II算法具有更好的简便性与精确性，为工程项目多目标优化问题的处理构建了柔性的建模框架。通过NSGA-II算法得出的5组非支配最优组合均能满足集对分析法建立的多目标优化函数，达到质量、进度和成本3个方面的贴合度最高。

4 结论

通过集对分析法对工程项目质量-进度-成本的多目标优化进行了集对联系度的建模，为消除不同指标之间的耦合，利用NSGA-II算法对多目标优化问题进行了求解，有利于提高工程项目资源配置计划的合理性和科学性。NSGA-II算法给出了在相对确定研究背景下的所有最优解集合，可方便决策者根据实际作业需求和施工参数要求对优化结果进行选取。算例结果表明，运用集对分析法和NSGA-II算法解决工程项目多目标优化问题是可行且有效的。

[1] 李雪淋，王卓甫.基于向量评价遗传算法的工程项目多目标优化[J].水运工程，2007(11):9-12.

[2] BADU A J G，SURESH N. Project management with time，cost and quality considerations[J].Eurapear Journal of Operational Research，1996,88(2):320-327.

[3] 马超，张松，李玉东，等.考虑风险的大型工程项目多目标均衡优化[J].计算机工程,2013,39(2):270-278.

[4] 陈勇强，高明，张连营.基于遗传算法和Pareto排序的工期-费用-质量权衡模型[J].系统工程理论与实践，2010,30(10):1774-1780.

[5] 赵克勤.集对分析及其初步应用[M].杭州：浙江科学技术出版社，2000:45-101.

[6] WILLIS H L，ENGEL M V. Optimization applications to power distribution[J]. IEEE Computer Applications in Power,1995,8(4):12-17.

[7] SRINIVAS N,DEB K. Multi-objective optimization using non-dominated sorting in genetic algorithms[J]. Evolutionary Computation,1995,2(3):221-248.

[8] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II[J]. Parallel Problem Solving from Nature PPSN VI Lecture Notes in Computer Science,2000(1917):849-958.

ZHAI Rui:Postgraduate; School of Business, Hohai University, Nanjing 211100, China.

[编辑：王志全]

Project Multi-objective Scheduling Optimization Based on Set Pair Analysis and NSGA-II

ZHAIRui,ZHANGYunning,CHENGuowei,ZHAOYingliang

The three main objectives of the project are schedule, cost, and quality, which are the unity of opposites. The optimization of the multi-objectives of the project focuses on seeking the harmony of the three of them. Constrained by the threshold level of the project schedule, cost and quality, a flexible modeling framework was constructed for the construction of multi-objective optimization problem by set pair analysis method. Then NSGA-II algorithm was used to solve the model of multi objective optimization in order to get multi-objective optimization of Pareto optimal solution set. Finally, a practical example was given to verify the feasibility and effectiveness of the algorithm in solving multi-objective optimization project problems.

project; multi-objective optimization; set pair analysis; Pareto solution set; NSGA-II algorithm

2015-04-31.

翟瑞(1993-)，女，安徽芜湖人，河海大学商学院硕士研究生.

校企合作科研基金资助项目(1063-51063213).

2095-3852(2015)06-0735-05

A

TU712.1

10.3963/j.issn.2095-3852.2015.06.016