基于备用覆盖的应急服务设施选址问题研究

万 波，万 敏

(1.江汉大学 教务处，湖北 武汉 430056；2.江汉大学 数学与计算机科学学院，湖北 武汉 430056)



基于备用覆盖的应急服务设施选址问题研究

万 波1，万 敏2

(1.江汉大学 教务处，湖北 武汉 430056；2.江汉大学 数学与计算机科学学院，湖北 武汉 430056)

当重大灾害事件发生时，需要调动大量应急服务设施投入到救援工作中，备用覆盖是提高应急服务设施调度效率，改进设施可达性的有效方法。在考虑传统的最大覆盖基础上，综合考虑首次覆盖人口最大化、备用覆盖人口最大化和非覆盖范围内总的旅行成本最小化3个目标，建立了基于备用覆盖的应急服务设施选址模型。以武汉市某区急救中心选址为例，利用FGP方法将模糊的多目标问题转化为确定的单目标问题，并利用LINGO求解。结果表明，FGP方法是一种求解基于备用覆盖的应急服务设施选址模型的有效方法。此外，还对FGP的3种常用方法求解效率进行了比较与分析。

备用覆盖；模糊目标规划；应急服务；设施选址

应急服务设施选址是应急管理领域的核心，其已成为选址问题研究的重要分支[1-2]。当重大灾害事件发生时，需要调度大量的应急服务设施开展救援工作，从而尽量避免人员伤亡和财产损失。对应急服务设施进行科学规划与合理布局，提高调度效率，满足公众对应急服务设施服务均等化、高质量的需求具有重要意义[3]。

传统的选址问题包括覆盖问题、中心问题及中位问题。在应急服务设施选址领域，覆盖问题是研究和讨论最多的问题。经典的覆盖问题包括集合覆盖问题(SCLP)与最大覆盖问题(MCLP)。扩展的覆盖问题包括备用覆盖、逐渐覆盖及合作覆盖等。应急服务对设施在规定时间内的可达性和服务能力要求较高，需要服务设施对需求点提供备用覆盖，以保证其服务能力，同时提高系统调度效率。因此，备用覆盖已广泛应用于应急公共服务设施选址领域。DASKIN等首先提出了备用覆盖的概念，允许在覆盖范围内的设施对其他需求点提供应急服务，并对EMS系统车辆选址问题进行了研究[4]。HOGAN等提出了两个备用覆盖模型：BACOP1和BACOP2。BACOP1是在传统的集合覆盖基础上考虑了被两次覆盖的需求最大化；BACOP2是在最大覆盖基础上考虑了两次覆盖需求最大化[5]。ARAZ等将BACOP2进行扩展，考虑了最小化非覆盖范围内的旅行距离[6]。ERDEMIR等引入备用覆盖的概念，对地面和空中医疗设施联合选址问题进行了研究[7]。葛春景等针对重大突发事件应急响应的特点，在满足基本覆盖要求的同时，对重要的需求点进行多重覆盖，建立了满足不同服务质量水平下的多重覆盖模型(MQCLP)[8]。肖俊华等基于备用覆盖和渐近覆盖等思想，建立了应急物资储备库多级覆盖选址模型，并利用遗传算法求解[9]。付德强等考虑储备库的建设成本、重要地区的备用覆盖等因素，建立了应急储备库多目标选址模型，并利用NSGA-Ⅱ求解[10]。

笔者研究了一类基于备用覆盖的应急服务设施选址问题，在传统的最大覆盖基础上，综合考虑备用覆盖及非覆盖范围内总的旅行成本目标，建立了相应模型。考虑到应急服务设施选址问题目标期望值的不确定性，笔者引入模糊目标规划方法对基于备用覆盖的应急服务设施选址问题进行求解。

1 模型的建立

1.1 模糊目标规划

随着应急设施选址问题研究的不断深入，传统的确定性选址理论已不能满足需要，不确定性、随机性选址问题越来越引起研究者的重视。模糊理论作为定量决策与定性决策的桥梁，用于处理非明确定义的准则与标准的度量方法，被引入应急设施选址领域[11]。ZADEH将模糊集理论引入目标规划中，提出了模糊目标规划(fuzzy goal programming，FGP)方法。其基本思路是构造隶属度函数，利用隶属度函数刻画各目标与目标期望值之间的关系[12]。

对于求最小目标值和求最大目标值而言，线性隶属度函数定义分别如式(1)和式(2)所示,其几何形式分别如图1和图2所示。

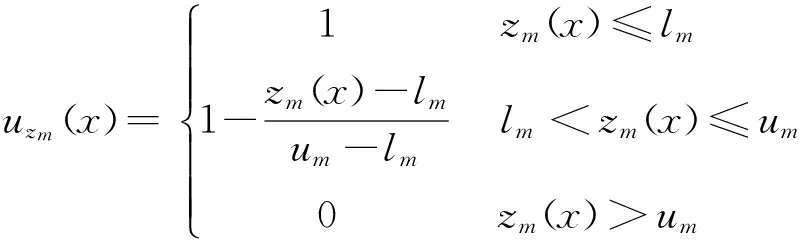
(1)

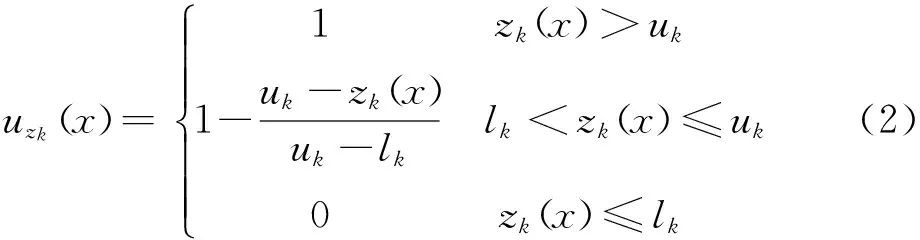
图1 线性隶属度函数uzm(x)几何形式

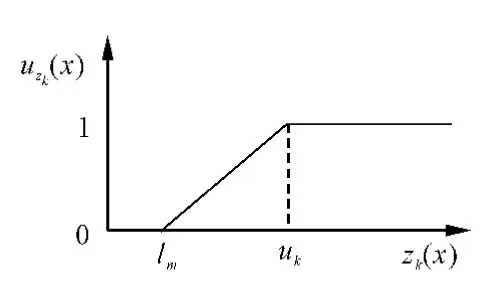
图2 线性隶属度函数uzk(x)几何形式

1.2 有关符号定义

笔者使用的相关符号定义如下：I为需求点集合，I={i|1,2，…,n}；J为设施候选点集合，J={j|1,2，…,k}；R为覆盖半径；hi为需求点i的需求量；kj为位于点j设施的服务能力；B为设施点的数量约束；dij为需求点i到设施点j的距离；aij的取值规则为如果dij≤R,则aij=1；否则aij=0；eij的取值规则为如果dij>R,则eij=1；否则eij=0；Fi的取值规则为如果需求点i被覆盖一次，则Fi=1；否则Fi=0；Si为需求点i被至少覆盖两次的人口份额。此外，将决策变量定义如下：zij为源于需求点i的需求分配给j点的份额；yj的取值规则为服务设施定位于j点，则yj=1；否则yj=0。

1.3 基于备用覆盖的应急服务设施选址模型

笔者建立了一个基于备用覆盖的应急服务设施选址模型(ESFLMBC)。该模型综合考虑了首次覆盖人口最大化、备用覆盖人口最大化，以及非覆盖范围内总的旅行成本最小化3个目标。该模型同时考虑了设施的服务能力约束及设施点的数目约束等条件[13]。

(3)

(4)

(5)

(6)

Si≤Fi,∀i∈I

(7)

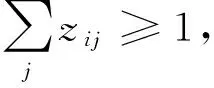
(8)

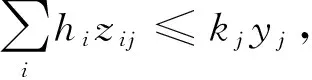
(9)

(10)

Fi∈{0,1},∀i∈I

(11)

Si∈[0,1],∀i∈I

(12)

zij∈[0,1],∀i∈I,∀j∈J

(13)

yj∈{0,1},∀j∈J

(14)

其中:式(3)为首次覆盖的人口最大化；式(4)为备用覆盖的人口最大化；式(5)为非覆盖范围内总的旅行成本最小化；式(6)表示确定可覆盖需求点的设施数量；式(7)表示当首次覆盖出现的情况下才存在备用覆盖；式(8)表示每个需求点所产生的需求均得以满足；式(9)表示分配给一个设施点的总人口数不超过该点设施的服务能力，同时保证需求仅仅分配给有设施的选址点；式(10)为设施点的数目约束；式(11)和式(12)分别对中间变量Fi和Si进行定义，其中，Si可以不为整数，说明允许第二次覆盖为部分覆盖，其目的是保证尽可能多的点可获得二次覆盖，从而提高系统的运作效率；式(13)和式(14)分别对决策变量zij和yj进行定义。

2 求解算法

2.1 常用的FGP方法

常用的模糊目标规划方法有FGP-C(经典的FGP)、FGP-W(加权的FGP)和FGP-P(带优先级的FGP)3种。

(1)FGP-C。ZIMMERMANN将辅助变量λ引入模糊目标规划，建立了FGP-C模型[14]：

maxZ=λs.t.uZk(x)≥λk=1,2,…,mgj(xi)≤bjj=1,2,…,Jxi≥0i=1,2,…,n0≤λ≤1

(2)FGP-W。TIWARI等给出了FGP-W模型，wk表示第k个目标的权重，模型如下[15]：

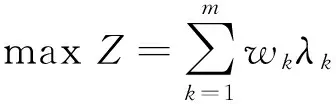
(3)FGP-P。CHEN等给出了FGP-P模型。设存在4个目标，其优先级为：λ1≥λ3,λ4≥λ3,λ3≥λ2，则FGP-P模型如下[16]：

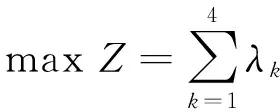
2.2 求解过程

笔者利用模糊目标规划(FGP)的方法将基于备用覆盖的应急服务设施选址模型转化为确定的单目标的模型，然后利用LINGO求解。以FGP-W为例，将求解算法分成两个部分。先利用LINGO求出每个目标的上下界，即可给出每个目标的隶属度函数[17]。再利用FGP-W方法，将多目标问题转化为单目标问题，使用LINGO求解。

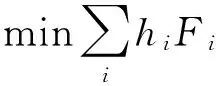
(2)利用FGP-W，将多目标问题转化为单目标问题求解。将uz1(x)、uz2(x)和uz3(x)作为约束条件加入FGP-W模型中，并将式(6)～式(14)代入，可得如下模型，并使用LINGO求解。

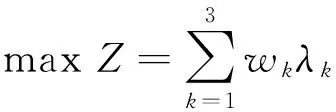
同理，运用LINGO可求得FGP-C和FGP-P方法相应的解。

3 案例分析

笔者以武汉市某区急救中心选址为案例进行分析。根据该区的地理位置与人口分布状况，将居民点聚类成50个需求点，即I={i1，i2，…，i50}，设施候选点集合与居民点集合一致，即J=I={i1，i2，…，i50}。假设需要建立10个急救中心，每个急救中心的服务能力kj=1 000人。hi为50个居民区的需求人口数。由于dij、hi数据量大，在此不一一列出。假设覆盖半径R=1.5 km。利用LINGO11软件，分别求出每个目标的上界与下界：{u1,l1}={0,7 343}，{u2,l2}={0,4 670}，{u3,l3}={10 296 478,204 095 006}。根据线性隶属度函数定义，可得3个目标的隶属度函数为：

将u1(x)、u2(x)、u3(x)代入FGP-W模型，可得：

0≤λk≤1,k=1,2,3

另外，加上约束条件式(6)～式(14)。

用LINGO求解以上模型，其结果如表1所示。同理可得FGP-C，FGP-P方法的求解结果。选取传统的多目标问题求解方法，即线性加权法WLM进行求解，以便与FGP方法的求解效果进行比较。这4种方法的求解结果如表1所示。

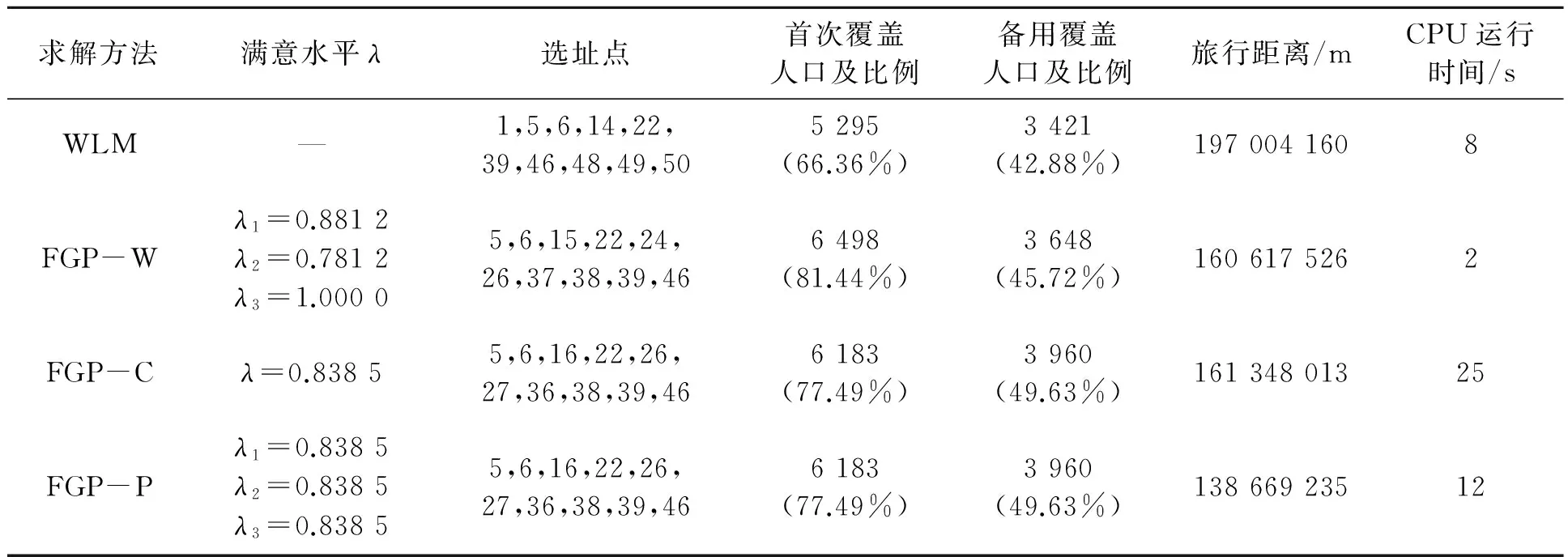
表1 各种方法求解结果

注：WLM与FGP-W求解方法中的w1=0.6,w2=0.3,w3=0.1。

(1)FGP与WLM比较。由表1可以看出，FGP-W、FGP-C、FGP-P与WLM相比，其首次覆盖的人口、备用覆盖的人口均大于WLM，非覆盖范围内的旅行距离均小于WLM，也就是说，FGP 3种方法的3个目标值均优于WLM。其原因在于模糊目标规划确定了各目标的上下界，虽然是模糊的，但可在各自范围内进行调整与优化，以寻求较为满意的解，这比WLM指定各目标的权重更切合实际情况，因而能够达到较好的求解质量。此外，从CPU运行时间来看，FGP的3种方法均比WLM快。因此，相比传统的WLM方法而言，FGP方法是一种求解多目标问题的高效率、高质量的方法，特别是在目标期望值不确定的情况下，求解优势更加明显。

(2)FGP各方法比较。就FGP-W与FGP-C而言，FGP-W的首次覆盖的人口及比例均比FGP-C高，同时，非覆盖范围内的旅行距离比FGP-C要小，但备用覆盖的人口及比例比FGP-C要低，这说明FGP-W通过牺牲第二目标而获得了较好的第一目标与第三目标，体现了各目标之间的背反规律。

就FGP-C与FGP-P而言，前者的总体满意水平λ=0.838 5，后者的3个目标的满意水平为λ1=λ2=λ3=0.838 5，两者的满意水平完全相同，体现在目标函数上第一、第二目标值完全相同，其设施选址点也完全一样。但FGP-P的第三目标值更优，这是由于FGP-P规定了各目标的优先级，从而导致决策变量zij不同。两者相比较而言，如果看重第三目标，宜选择FGP-P模型。

就FGP-W、 FGP-C与FGP-P三者比较来看，在所求的第一目标值结果中，FGP-W的结果最优。原因在于FGP-W确定了第一目标的权重w1=0.6，其权重明显高于第二和第三目标。同时，从CPU运行时间来看，3种方法中FGP-W的运行时间最短。因此，对于重视第一目标，需提高首次覆盖人口及比例，同时考虑CPU运行效率的情况下，可利用FGP-W求解。对于重视第二目标，需提高备用覆盖人口及比例，可采用FGP-C或者FGP-P模型。从CPU运行时间来看，FGP-W和FGP-P相对于FGP-C而言，均有明显的提高，其中，FGP-W的运行时间最短。如果是在重视第二目标的同时，兼顾CPU运行效率的话，宜选择FGP-P模型。

4 结论

笔者研究了一类基于备用覆盖的应急服务设施选址问题，综合考虑了传统的首次覆盖的人口最大化、备用覆盖的人口最大化及非覆盖范围内系统总的旅行成本最小化这3个目标，建立了相应模型。以武汉市某区急救中心选址为例进行案例分析，利用FGP方法将多目标问题转化为单目标问题，并利用LINGO求解。研究结果表明，FGP方法是一种有效求解基于备用覆盖的应急服务设施选址模型的方法，能够生成更为客观灵活的满意解。同时，笔者对FGP各方法的求解进行了比较与分析，为决策者在不同的环境下有选择性地采用FGP方法提供了参考意见。

[1] 张铱莹.多目标应急服务设施选址与资源配置问题研究[J].中国安全科学学报,2011,21(12):153-158.

[2] 陆相林,侯云先.基于设施选址理论的中国国家级应急物资储备库配置[J].经济地理,2010,30(7):1092-1095.

[3] 李双琳,马祖军,郑斌,等.震后初期应急物资配送的模糊多目标选址-多式联运问题[J].中国管理科学,2013,21(2):144-151.

[4] DASKIN M S, STERN E H. A hierarchical objective set covering model for emergency medical service vehicle deployment[J].Transportation Science,1981(15):137-152.

[5] HOGAN K, REVELLE C S. Conception and applications of backup coverage[J]. Management Science, 1986(32):1432-1444.

[6] ARAZ C, SELIM H, OZKARAHAN I. A fuzzy multi-objective covering-based vehicle location model for emergency services[J].Computers & Operations Research, 2007(34):705-726.

[7] ERDEMIR E T, BATTA R, ROGERSON P A, et al. Joint ground and air emergency medical services coverage models: a greedy heuristic solution approach[J]. European Journal of Operational Research, 2010,207(2):736-749.

[8] 葛春景,王霞,关贤军.重大突发事件应急设施多重覆盖选址模型及算法[J].运筹与管理,2011,20(5):50-56.

[9] 肖俊华,侯云先.应急物资储备库多级覆盖选址模型的构建[J].统计与决策,2012(23):45-48.

[10] 付德强,王旭,张伟.基于NSGA-Ⅱ的应急储备库多目标选址决策模型及算法研究[J].运筹与管理,2014,23(4):64-69.

[11] 张宗祥,杨超,陈宗武.基于服务质量的多目标逐渐覆盖问题[J].公路交通科技,2013,30(10):93-146.

[12] ZADEH L A. Fuzzy sets[J]. Information and Control,1965,8(3):38-53.

[13] 万波.公共服务设施选址问题研究[D].武汉:华中科技大学,2012.

[14] ZIMMERMANN H J. Fuzzy programming and linear programming with several objective function[J].Fuzzy Sets and System,1978(1):45-55.

[15] TIWARI R N, DHARMAR S, RAO J R. Fuzzy goal programming:an additive method[J].Fuzzy Sets and Systems,1987(24):27-34.

[16] CHEN L H, TSAI F C. Fuzzy goal programming with different importance and priorities[J].European Journal of Operation Research,2001,133(5):48-56.

[17] 赵娟,陈华友.基于模糊需求的多产品供应商选择的多目标规划模型[J].模糊系统与数学,2011,25(4):148-155.

WAN Bo:Assoc. Prof.; Dept. of Academic affairs, Jianghan University, Wuhan 430056, China.

[编辑：王志全]

Location of Emergency Service Facilities Based on Backup Coverage

WANBo,WANMin

When disasters happen, it is necessary to put a wide variety of emergency services into the rescue work. The backup coverage is an efficient method to enhance the dispatching efficiency of emergency service facilities and it can improve the accessibility of facilities. Based on the traditional maximum coverage location model, a location model was established for emergency service facilities based on the backup coverage with the complex goals including the backup coverage and the total travel cost without the coverage area. An emergency center location problem in a district in Wuhan was analyzed. The fuzzy multi-objective problem was transferred into the certain single-objective problem by FGP method and LINGO soft was used to solve the problem. The result shows that FGP is an efficient method for the solution to the model. The solution efficiency of the three common methods of FGP was analyzed and compared with each other.

backup coverage; fuzzy goal programming; emergency services; facility location

2015-04-28.

万波(1972-)，男，湖北汉阳人，江汉大学教务处副教授;博士.

国家自然科学基金资助项目(71172093).

2095-3852(2015)06-0730-05

A

O22

10.3963/j.issn.2095-3852.2015.06.015