基于博弈论与改进TOPSIS的工程评标方法

王望珍，李金瑾

(武汉大学 土木建筑工程学院，湖北 武汉 430072)



基于博弈论与改进TOPSIS的工程评标方法

王望珍，李金瑾

(武汉大学 土木建筑工程学院，湖北 武汉 430072)

引入一种基于博弈论的组合赋权方法和使用灰色关联度改进TOPSIS法的排序方法对投标方案进行评价，并通过实例验证了该方法的有效性。该方法克服了传统TOPSIS法中出现的由于两方案的正、负欧氏距离相等而不能有效排序的缺陷，对进一步完善评标体系具有一定的参考价值。

评标方法；博弈论；灰色关联；TOPSIS法

随着招标工作的开展，传统的评标方法呈现很多的缺陷，为了在招标工作中做出正确的决策，不少学者对评标方案优选进行了研究。目前主要的评标方法有层次分析法[1]、模糊综合评价法[2]、价值工程法[3]、BP神经网络[4-5]等。层次分析法虽然能对评价方案进行系统分析，但该方法中定性的成分较多；模糊综合评价法对那些模糊的并且不容易量化的问题有较强的适用性，但在一定的情况下会出现超模糊现象，使评价效果不佳；价值工程法为评标提供一种定量分析方法，但该方法需要比较详尽的数据信息，才能得出准确的结果，因此在实际运用上难度较大；BP神经网络评标模型，虽然降低了权重确定中的主观影响，但该方法需要一定的数据支撑，并且评价精度不高。笔者在已有评价指标的基础上，引入博弈论的组合赋权方法，使指标权重的确定更科学、合理，再运用灰色关联度和逼近理想解的排序方法对各投标方案进行评价，最后通过工程实例验证了该方法的有效性。它不但能够反映各备选方案在距离上与理想方案的接近性，还能够通过几何曲线的形状来反映与理想方案的接近程度，对工程项目评标具有一定的指导作用。

1 评价指标权重的确定

确定指标权重的方法主要有以下3类：①主观赋权法，主要凭借专家的知识和经验来确定指标权重[6]，权重值的确定能结合评价对象的实际情况，但容易受专家知识经验不足、个人偏好的影响；②客观赋权法，主要根据原始数据之间的关系，通过一定的数学方法来确定权重，客观性较强，但有时会与实际情况偏离；③组合赋权法，可以实现主、客观赋权法的优势互补，使权重结果既结合专家意愿又忠于数据本身。因此，笔者采用AHP确定主观权重，信息熵法确定客观权重 ，并引入基于博弈论的组合赋权法确定综合权重。

1.1 主、客观权重的确定

层次分析法是一种多目标决策方法，它把一个复杂问题通过层层分解的形式，将组成因素按支配关系分为目标层、准则层和指标层等几个基本层次[7]。通过定性指标模糊量化，综合方案数据和专家意见，科学地确定指标权重。熵值可以度量系统的无序性、随机性。信息熵法就是通过判断评价指标离散程度的大小来确定权重。离散程度越大，该指标在评价中的权重越大[8]。

1.2 基于博弈论的组合赋权法

博弈论是在综合考虑不同行为主体的行动集之后，研究该决策活动优化策略的方法。通过博弈论来确定综合权重，就是在不同权重方法确定的权重向量集里，寻找不同评价指标之间的一致或妥协，使可能的权重与各个基本权重的偏差达到最小化[9]。该方法比一般将主客观权重简单加权平均更科学、合理。其基本步骤如下：

(1)假设使用S种方法对评价指标进行赋权，得到S个指标权重向量，可以构造一个基本权重集U={u1,u2,…，uS}，记这S个向量的任意线性组合为：

其中，αk为权重系数，且αk>0。

(2)对S个线性组合系数αk进行优化，从而使u与各uk的离差极小化，即：

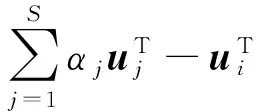
然后求出式(1)的最优化一阶导数条件:

(2)

则式(2)对应的线性方程组为：

(3)

(3)根据式(3)求出(α1,α2,…,αS)，对其进行归一化处理：

(4)

最后得出综合权重为：

(5)

2 评标模型的建立

TOPSIS法是多目标决策分析中的一种有效方法，由于该方法几何意义简单明了，在方案优选问题中应用广泛。但传统的TOPSIS法存在缺陷：它不能评价距正理想解和负理想解相等的点所在线上的方案，因为该情况下评价方案的贴近度相等，TOPSIS法不能得出哪个方案较优。传统的TOPSIS法是从距离方面来反映各评价方案与理想方案的接近程度，不能很好地反映方案内部各因素变化趋势与理想方案之间的区别[10]；而灰色关联法是从形状相似性反映各评价方案与理想方案的接近程度[11]，可以弥补这一缺陷。因此笔者引进一种灰色关联改进的TOPSIS决策方法，使得方案排序更合理。决策模型构建过程如下：

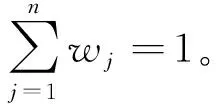
(2)指标矩阵标准化。 按照式(6)和式(7)对原始指标矩阵X=(xij)m×n进行规范化处理，得到无量纲化指标矩阵Y=(yij)m×n。

对于效益型评价指标，则为：

(6)

对于成本型评价指标，则为：

(7)

(3)计算加权标准化指标矩阵：

Z=(zij)m×n

(8)

其中，zij=wjyij。

(4)确定正理想解z+与负理想解z-:

(9)

(10)

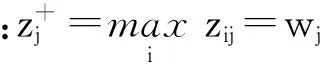
(11)

(12)

(6)计算各方案与正理想解和负理想解的灰色关联矩阵R+和R-：

(13)

(14)

其中，ρ∈(0,1)为分辨系数。

(7)计算各方案与正理想解和负理想解的灰色关联度r+和r-:

(15)

(16)

(17)

(18)

(19)

(20)

(9)计算相对贴近度：

(21)

(22)

(23)

其中,e1，e2反映决策者对位置与形状的偏好程度，e1+e2=1，e1与e2由决策者的偏好决定。

(11)相对贴近度排序。根据δi的大小进行方案优劣排序，δi越大，表示该方案越贴近正理想方案，方案越优；反之方案越劣。

3 工程实例分析

某建筑工程进行公开招标，经过资格预审，共有5家合格的投标单位，分别记为A、B、C、D、E。结合该工程的实际情况，所构建的评价指标体系由7个指标构成，其中工程报价、施工工期、类似工程累计施工面积、企业财务状况直接采用投标书上的相关数据；施工组织设计、质量保证体系、投标人及项目经理业绩则通过专家打分使定性指标定量化。各投标单位的评标数据如表1所示。

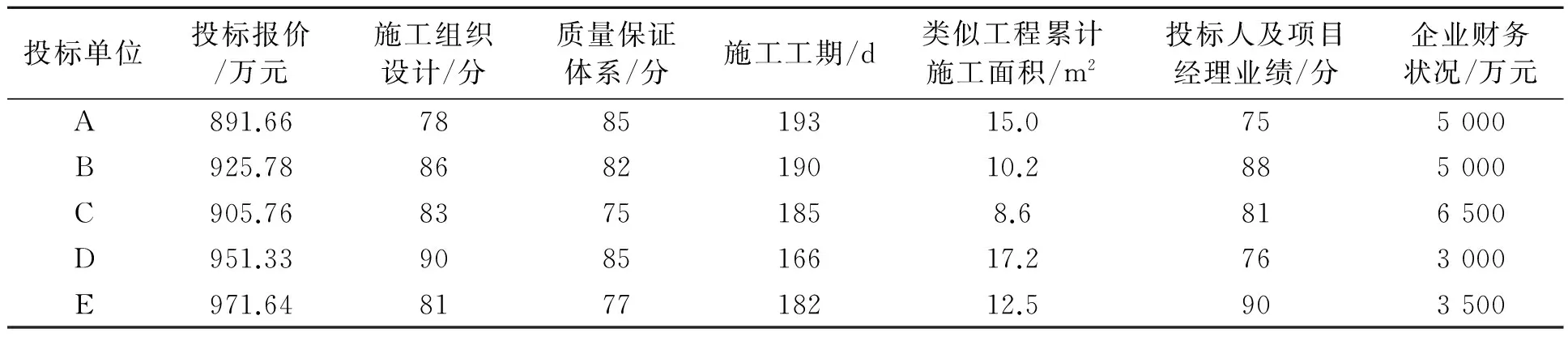
表1 投标单位评标指标数据表

(1)权重计算。采用文献[12]的层次分析法和熵权法确定主客观权重，然后根据式(3)～式(5)得到组合权重w=(0.380 3,0.132 9,0.067 0,0.139 5,0.074 1,0.108 8,0.099 1)。

(2)根据表1构建原始矩阵：

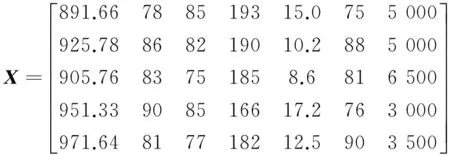
(3)根据式(6)和式(7)对原始矩阵X进行无量纲化，得标准化指标矩阵Y：

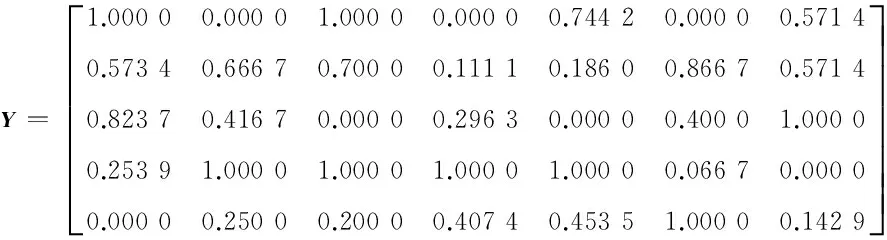
(4)根据式(8)计算加权标准化矩阵Z：

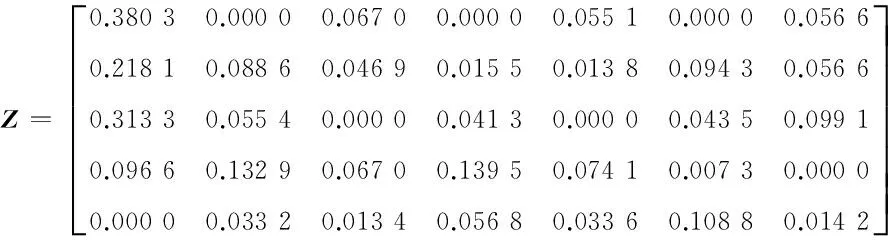
(5)计算欧氏距离和灰色关联度。根据式(9)和式(10)分别确定加权标准化矩阵Z的正理想解和负理想解：Z+=[0.380 3,0.132 9,0.067 0,0.139 5,0.074 1,0.108 8,0.099 1]，Z-=[0,0,0,0,0,0,0]。采用式(11)和式(12)计算各评价方案到正、负理想解的欧氏距离：d+=(0.226 1,0.221 6,0.065 3,0.317 2,0.416 1)，d-=(0.394 2,0.264 8,0.338 6,0.237 7,0.133 0)。再根据式(13)和式(14)得到各方案与正、负理想解的灰色关联矩阵分别为：

然后根据式(15)和式(16)得到各评价方案与正、负理想解的灰色关联度：r+=(0.600 0,0.547 6,0.486 9,0.726 2,0.488 8)，r-=(0.647 9,0.527 4,0.634 3,0.506 4,0.652 4)。

(6)计算相对贴近度。根据式(17)～式(20)对欧氏距离和灰色关联度进行无量纲化处理得：D+=(0.543 4,0.532 6,0.156 9,0.762 3,1.000 0)，D-=(1.000 0,0.671 7,0.859 0,0.603 0,0.337 4)，R+=(0.826 2,0.754 1,0.670 5,1.000 0,0.673 1)，R-=(0.993 1,0.808 4,0.972 3,0.776 2,1.000 0)。根据式(21)和式(22)分别计算关于欧氏距离和灰色关联度与正理想解的接近度：T+=(0.647 9,0.557 8,0.845 6,0.441 7,0.252 3)，S+=(0.454 1,0.482 6,0.408 1,0.563 0,0.402 3)。然后根据式(23)计算相对贴近度，取e1=e2=0.5，则δ=(0.551 0,0.520 2,0.626 9,0.502 4,0.327 3)。

(7)根据相对贴近度，得到的排序结果为C>A>B>D>E。笔者的排序结果与传统TOPSIS法排序结果一致，验证了改进方法的有效性，该方法克服了传统TOPSIS法的缺陷。

4 结论

笔者在已有评价指标的基础上，引入基于博弈论的组合赋权法，将层次分析法和信息熵法得到的权重进行组合，与简单的线性加权相比，该方法更加科学合理。改进了传统TOPSIS法在工程评标中的不足，构建了灰色关联逼近理想解的方法，有利于完善工程项目评价方法体系。

[1] 樊胜军.层次分析法在建设工程评标中的应用[J].西安建筑科技大学学报,2003(8):35-38.

[2] 刘亚丽.工程项目招标评标方法研究[D].天津：天津大学,2003.

[3] 李霞.基于价值工程的工程量清单计价模式评标方法研究[D].天津：天津大学,2008.

[4] 吴高莉.建设工程施工项目评标决策支持系统研究[D].武汉：武汉理工大学,2006.

[5] 周丹.建设工程施工招标评标系统方法的研究[D].大连：大连理工大学,2005.

[6] 郑绍羽,李素芹.混合型指标基坑支护方案优选的改进TOPSIS法[J].中国安全科学学报,2014(5):19-20.

[7] 李俊玲.河流健康评价指标体系及权重模型研究[D].南京:河海大学,2008.

[8] 陈伟,夏建华.综合主客观权重信息的最优组合赋权方法[J].数学的实践与认识,2007,37(1):17-22.

[9] 路遥,徐林荣,陈舒阳,等.基于博弈论组合赋权的泥石流危险度评价[J].灾害学,2014,29(1):194-200.

[10] 李彦斌,于心怡,王致杰.采用灰色关联度与TOPSIS法的光伏发电项目风险评价研究[J].电网技术,2013,37(6):1514-1519.

[11] 尹清雨.基于TOPSIS法和灰色关联分析的多属性决策方法研究[D].重庆：重庆师范大学,2011.

[12] 杨宝臣,陈跃.基于组合赋权TOPSIS模型的项目评标方法研究[J].电子科技大学学报(社科版),2011(1): 8-9.

WANG Wangzhen:Assoc. Prof.; School of Civil Engineering, Wuhan University, Wuhan 430072, China.

[编辑：王志全]

Project Evaluation Method Based on Game Theory and Improved TOPSIS

WANGWangzhen,LIJinjin

As projects just run for one time, the level of uncertainty in construction projects is much higher than that in other economic activities. For the construction unit, selecting one suitable contractor by a reasonable method is of great importance. A combination weighting approach based on game theory was introduced and, a sorting method of TOPSIS improved by gray correlation was utilized to evaluate the bid schemes. Verification by practical examples shows that the method is an effective method for evaluation. This method overcomes the problem in traditional TOPSIS method that sequencing problem arisen by identical distances of positive and negative Euclidean in two schemes cannot be solved effectively. It has guiding significance to perfect the evaluation system.

bid evaluation; game theory; gray correlation; TOPSIS method

2015-05-18.

王望珍(1968-)，女，湖北武汉人，武汉大学土木建筑工程学院副教授;博士.

教育部国家科技支撑计划基金资助项目(2014BAL05B00).

2095-3852(2015)06-0726-04

A

TU12

10.3963/j.issn.2095-3852.2015.06.014