一种抗蛇行减振器控制系统在高速动车组中的仿真应用
2015-02-15刘永强廖英英杨绍普赵志宏
刘永强, 廖英英, 杨绍普, 赵志宏
(1.石家庄铁道大学 机械工程学院,河北 石家庄 050043;2.石家庄铁道大学 土木工程学院,河北 石家庄 050043;3.河北省交通安全与控制重点实验室,河北 石家庄 050043;4.石家庄铁道大学 信息科学与技术学院,河北 石家庄 050043)
0 引言
列车在直线上高速运行时为了避免蛇行失稳,大多数情况下要求车体与构架间的纵向阻尼越大越好,而曲线通过时又要求纵向阻尼不能过大,以保证列车的安全性能。因此,在列车的历次提速过程中,横向稳定性和曲线通过性能一直都是难以解决的矛盾。工程师们不断优化悬挂参数和转向架结构,以协调两者间的关系最终实现整体均衡。但参数和结构优化所能达到的效果并非是永无止境的,当优化达到一定的程度后,横向稳定性与曲线通过性之间的矛盾将成为列车运行速度进一步提高的主要瓶颈[1-3]。
国内外专家学者针对横向稳定性和曲线通过性间的矛盾问题,提出了多种解决方案,如径向转向架[4-5]、倾摆式车体[6-7]、独立旋转车轮[8-9]、参数优化[10-11]等。这些方案虽然可以有效缓解这一矛盾,提高列车的整体动力学性能,但不能彻底地解决横向稳定性和曲线通过性能之间的根本矛盾。
本文提出一种抗蛇行减振器控制系统,可实现直线轨道和曲线轨道之间抗蛇行减振器阻尼系数的变化,使之在直线轨道上运行时采用较大的抗蛇行阻尼以保证车辆的横向稳定性能,而在通过曲线时切换为较小的阻尼来保证车辆的安全性能。采用ADAMS-Matlab联合仿真技术对该控制系统在高速动车组中的应用进行了仿真,以期解决列车横向稳定性与曲线通过性之间的矛盾问题。
1 高速动车组建模
利用铁道车辆动力学软件ADAMS/Rail建立某型300 km 级高速动车组模型,其中转向架模型和整车模型如图1和图2所示,模型考虑了车体、构架、轮对和轴箱的纵移、横移、沉浮、侧滚、点头和摇头共90个自由度,主要参数见表1。将动车组转向架模型中的抗蛇行减振器实体替换为作用力函数的形式,将作用力的大小定义为抗蛇行减振器阻尼系数c与减振器两端点间相对速度的乘积,其中阻尼系数c为状态变量形式。

图1 动车组转向架模型

图2 动车组整车模型

表1 动车组模型主要参数
2 横向稳定性与曲线通过性之间的矛盾
为了对比不同抗蛇行阻尼系数c时的车辆横向稳定性和曲线通过性能,分别计算c=0、5×104、1×105、5×105、1×106、5×106N·s/m 时车辆直线运行时的线性失稳速度和曲线通过时的最大脱轨系数。直线运行时采用350 km/h的速度运行在德国高干扰谱轨道上。曲线轨道的曲线半径为7 000 m,轨道超高为150 mm,车辆运行速度为250 km/h。
利用ADAMS/Rail计算线性失稳速度和最大脱轨系数的方法参见文献[12],仿真计算结果如图3和图4所示。当列车运行速度超过线性失稳速度时,蛇行运动幅值接近轮轨间隙,轮轨间发生剧烈的碰撞,将威胁到列车的运行安全。因此线性失稳速度越高,表示车辆的横向稳定性越好。列车通过曲线时的最大脱轨系数能直接代表该列车的安全性能,最大脱轨系数值越小,表明曲线通过性能越好、列车运行越安全。为了对比的一致性,将脱轨系数值取倒数后,与线性稳定速度一并进行归一化处理,如图5所示。从图5中可以看到,车辆的横向稳定性和曲线通过性是一对矛盾,两者随阻尼系数的变化趋势完全相反。因此,同时改善横向稳定性和曲线通过性能十分困难,而参数优化方法只能通过折中的办法确定阻尼系数。
3 抗蛇行减振器控制策略
车辆在不同线路上运行时最佳抗蛇行阻尼系数会有所不同,如在直线上运行时为了减小蛇行运动幅值要求阻尼系数越大越好,而在曲线轨道上运行时为了保持一定的姿态通过曲线,则要求阻尼系数不能过大。那么如果存在一种控制方法,能在直线和曲线线路间将动车组抗蛇行阻尼系数切换为不同的值,那么就有可能彻底解决横向稳定性和曲线通过性之间的矛盾。根据这一思路提出一种抗蛇行减振器控制系统,通过设定合理的状态指标,自动判断列车是在何种线路状况下运行,从而调整抗蛇行阻尼系数的大小,使之同时保证最优的车辆横向稳定性和曲线通过性能。
从图3可知,抗蛇行阻尼系数越大,车辆的横向稳定性越好,但真实情况下抗蛇行减振器可提供的阻尼力不可能无限大。考虑到目前国内外技术的允许范围,阻尼系数取最大极限值1×107N·s/m。为了准确找出曲线通过时的最优阻尼系数,设置抗蛇行阻尼系数取值范围为[1×1052×106],步长取值为1×105N·s/m。采用ADAMS/Rail进行仿真,仿真结果如图6所示。

图3 线性失稳速度随阻尼系数的变化
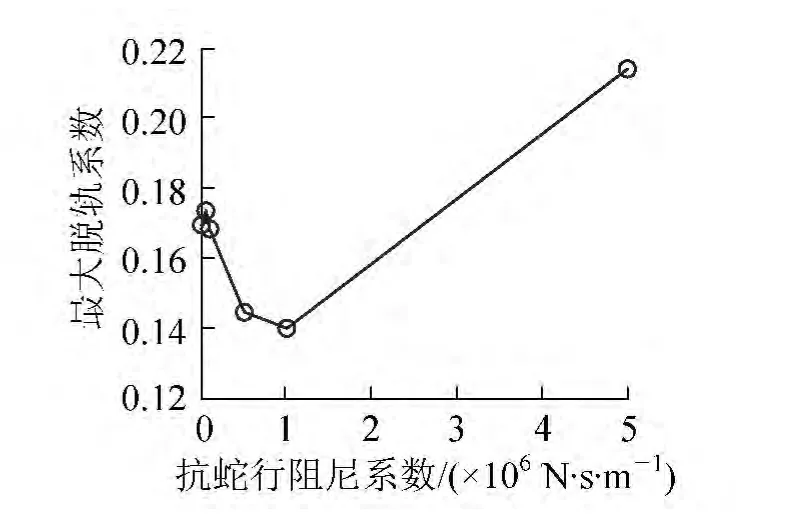
图4 最大脱轨系数随阻尼系数的变化
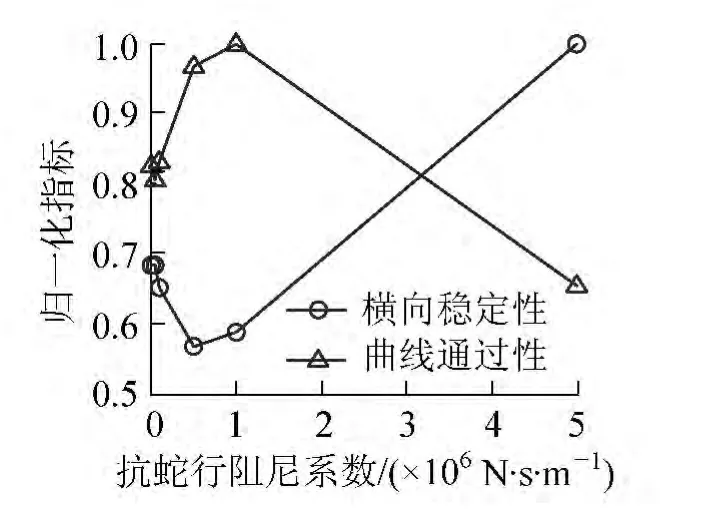
图5 车辆横向稳定性与曲线通过性

图6 曲线通过时抗蛇行阻尼系数优化
从图6中可知,曲线通过时脱轨系数最小时的阻尼系数为6×105N·s/m,将此数值作为动车组运行在曲线上时的最优阻尼系数。理想情况下,抗蛇行减振器控制系统执行在直线轨道运行时取大值,在曲线轨道运行时取小值的策略。那么该控制策略中用来判断直线和曲线线路的切换参数将是至关重要的。当高速动车组通过曲线时,由于存在曲线超高,车体左右两侧垂向位置会发生变化。图7为动车组以250 km/h匀速通过曲线半径为7 000 m,轨道超高为150 mm 的线路时的车体两侧高度差变化与直线轨道运行情况的对比。直线轨道采用德国高干扰谱,车速为350 km/h。从图7中可以看到,与直线轨道运行相比,通过曲线时车体侧滚非常明显,车体两侧垂向相对位移可高达80 mm。因此,可以将车体两侧高度差作为控制系统中曲线轨道的判据,切换阈值取为10 mm,以避免直线运行时轨道激扰造成的误判。
根据以上分析,该动车组模型的抗蛇行减振器控制策略可表示为

式中,cs为控制器输出的阻尼系数;c1和c2分别是在直线轨道和曲线轨道上运行时的最佳阻尼系数;Δy为车体两侧垂向相对位移。
4 基于联合仿真技术的抗蛇行减振器控制系统仿真分析
在ADAMS中建立动车组一系列状态变量,如构架质心摇头角、轮对横移量、车体横向加速度、轮轨间横向及垂向作用力等,将这些变量定义为输出变量。将之前定义的阻尼器阻尼系数定义为输入变量。将ADAMS中的高速动车组模型导入到Matlab/Simulink软件中,搭建高速动车组抗蛇行减振器控制系统,如图8所示。控制器的表达式如式(1)所示,它的两个输入变量分别是车体两侧侧壁中心点的垂向位移,输出为调节后的抗蛇行阻尼系数。
为了考察抗蛇行控制的效果,设置轨道为光滑轨道,曲线半径2 200 m,模拟动车组以200 km/h的速度通过曲线,仿真步长0.005 s,时长30 s。图9~图12分别为在无控制和有控制下高速动车组曲线通过时的脱轨系数、轮重减载率、轮轴横向力和轮轨垂向力。

图7 直线与曲线轨道上车体两侧垂向相对位置

图8 高速动车组抗蛇行减振器控制系统
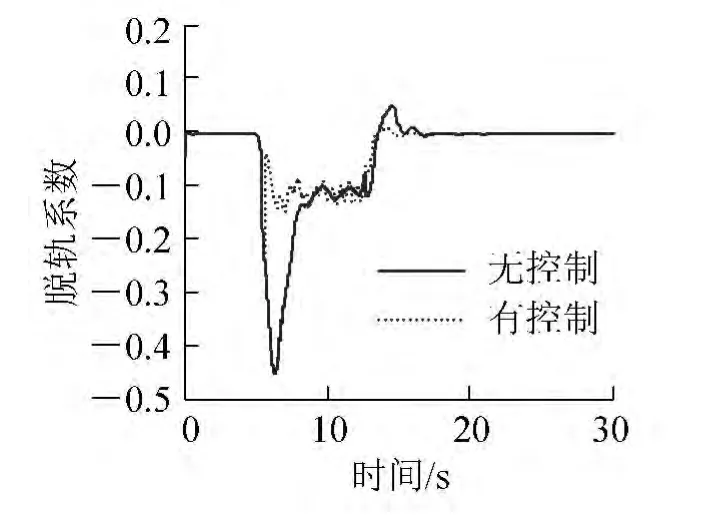
图9 抗蛇行控制下模型曲线通过时的脱轨系数

图10 抗蛇行控制下曲线通过时的轮重减载率
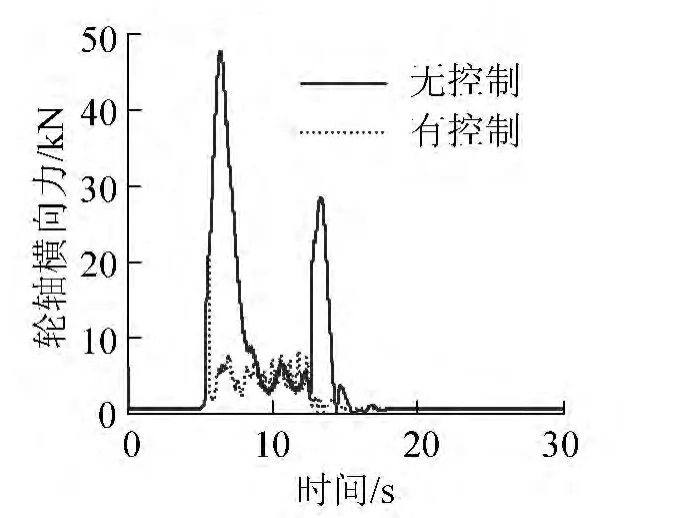
图11 抗蛇行控制下模型曲线通过时的轮轴横向力

图12 抗蛇行控制下模型曲线通过时的轮轨垂向力
从图9~图12中可以看到,与无控制相比,抗蛇行控制可以大大降低动车组曲线通过时的安全性指标,最大通过系数由0.45降到了0.24,降幅达47%。轮重减载率由0.47降到了0.3,降幅约36%。最大轮轴横向力从47.5 kN 降到了20.9 kN,降低了56%。轮轨间最大垂向力从105.9 kN 降到了97.8 kN,降低了7.6%。另外,经过在直线轨道上进行仿真计算,发现有控制与无控制效果相同,这是因为在直线轨道上两者的抗蛇行阻尼系数相等。在硬件实现方面,抗蛇行减振器控制系统输入所需的车体两侧高度差可由空气弹簧高度控制阀和压差阀直接获得,不需要额外的传感器设备,所以很容易实现。
5 结论
针对高速动车组横向稳定性与曲线通过性之间的矛盾,采用ADAMS-Matlab联合仿真的方法研究了抗蛇行减振器的控制问题,使得动车组在直线轨道上采用较高的阻尼系数,在通过曲线时调整为较低的阻尼系数。仿真结果发现,在不影响横向稳定性的前提下,抗蛇行减振器控制系统使得动车组通过曲线时的安全性指标大大降低,最大脱轨系数、轮重减载率、轮轴横向力和轮轨垂向力降幅分别降低了47%、36%、56%和7.6%,极大地提高了高速动车组的曲线通过性能。
[1]Polach O,Kaiser I.Comparison of methods analyzing bifurcation and hunting of complex railVehicle models[J].Journal of Computational and Nonlinear Dynamics,2012,7(4):1-8.
[2]刘建新,王开云.抗蛇行减振器对机车运行平稳性的影响[J].交通运输工程学报,2006,6(4):1-4.
[3]Simson SA,Cole C.Simulation of traction curving for active yaw-force steered bogies in locomotives[J].Proceedings of the Institution of Mechanical Engineers Part F-Journal of Rail and Rapid Transit,2009,223(1):75-84.
[4]马卫华,罗世辉,王自力.径向转向架机车垂向振动问题分析[J].机械工程学报,2007,43(4):65-69.
[5]Matsumoto A,Sato Y,Ohno H.Curving performance evaluation for active-bogie-steering bogie with multibody dynamics simulation and experiment on test stand[J].Vehicle System Dynamics,2008(46):191-199.
[6]罗仁,曾京.摆式列车主动倾摆控制的数值仿真研究[J].铁道学报,2006,28(5):28-34.
[7]Chli J.Prediction of displacement induced by tilting trains running on ballasted tracks through measurement of track impact factors[J].Engineering Failure Analysis,2013(31):360-374.
[8]池茂儒,张卫华,曾京,等.独立轮对柔性耦合径向转向架的导向特点[J].中国铁道科学,2007,28(5):93-97.
[9]Chao Y,Kwak J.Development of a new analytical model for a railway vehicle equipped with independently rotating wheels[J].International Journal of Automotive Technology,2012,13(7):1047-1056.
[10]郝建华,曾京,邬平波.铁道客车垂向随机减振及悬挂参数优化[J].铁道学报,2006,28(6):35-40.
[11]He YP,Mcphee J.Optimation of curving performance of rail vehicles[J].Vehicle System Dynamics,2005,43(12):895-923.
