导航卫星非差精密定轨测站选取策略分析

党金涛 郭东晓 李建文 魏 勇

1 信息工程大学导航与空天目标工程学院，郑州市科学大道62号，450001

20世纪70年代，随着GPS的建成运行，GNSS卫星精密定轨技术开始起步与发展［1］。自1993年IGS成立以来，GNSS卫星定轨精度得到不断提高［2］。为了促进GNSS的融合与发展，全球连续监测评估系统（international GNSS monitoring and assessment system，iGMAS）应运而生，其跟踪网数据对GNSS卫星精密定轨定位将作出新的贡献。目前，IGS和iGMAS全球观测网站点已经超过500个，如何利用较少的测站数据，提高计算效率，并能达到足够高的定轨精度，显得至关重要。为此，本文深入研究非差精密定轨的数据处理方法，兼顾测站数量、观测数据质量以及测站地理分布，提出了一种完善的测站选取策略。为验证该策略的有效性，结合GPS实测数据，开展精密定轨实验，并初步分析了GPS定轨精度。

1 数据处理方法与策略

1.1 处理方法及策略

观测量采用伪距和相位非差消电离层组合，并对伪距进行相位平滑。基本观测方程为：

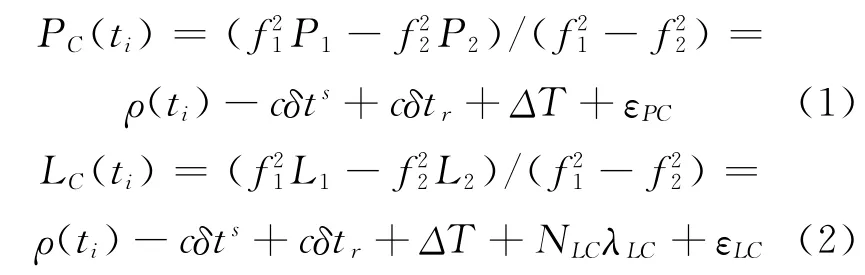
式中，P1、P2表示伪距观测量，L1、L2表示相位观测量，f1、f2表示双频载波的两个频率，ρ（ti）表示ti时刻的星地几何距离，c表示光速，δts和δtr分别表示卫星钟差和接收机钟差，ΔT表示对流层延迟，NLC表示消电离层组合相位的模糊度，λLC表示消电离层组合相位波长，εPC和εLC表示多路径效应、观测噪声及其他未模型化误差。对于未能模型化的误差，通过参数估计吸收［3］。

参数估计时，首先预消除历元参数（钟差参数），轨道解算完成后，再回代求解钟差参数［4］。对于对流层参数，干、湿分量分别处理，前者利用Saastamoinen模型进行改正，后者每2h 分段线性估计。地球自转参数和测站坐标采用IGS最终解并固定。由于非差模糊度与接收机和卫星的初始相位偏差不可分离［5］，模糊度参数采用浮点解。

1.2 数量质量控制策略

数据质量控制策略是否完善直接关系到定轨结果的好坏。在定轨过程中，首先采用TurboEdit自动编辑算法对非差数据进行预处理，并对伪距进行相位平滑［6］。

正常情况下，大部分的粗差和周跳可以得到很好的剔除和修复。对于没有修复的周跳，将定义新的弧段，并设置新的模糊度参数［7］。对未探测到的周跳与粗差观测值，在参数估计模块的残差编辑过程中进行处理。载波相位平滑后的伪距用于接收机时钟同步，同时利用伪距定位结果进一步剔除坏的测站［8］。数据迭代清理采用加权验后残差分析的方法。在残差编辑过程中，进一步剔除问题卫星和测站，并对较大的残差设置阈值（第一次取为20mm，第二次取为6mm）用于标记坏的观测历元。整个数据处理流程如图1所示。

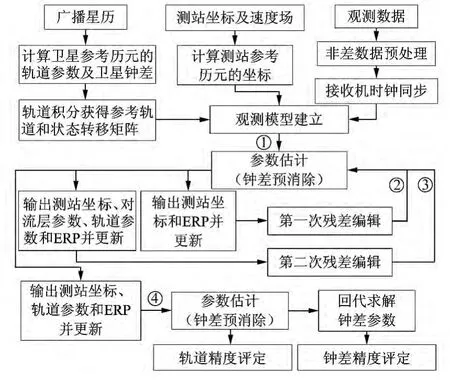
图1 数据处理流程Fig.1 Flow chart of data processing

1.3 测站选取策略

为分析测站地理分布对轨道误差的影响，可从观测方程进行推导。观测方程可简化表达为：

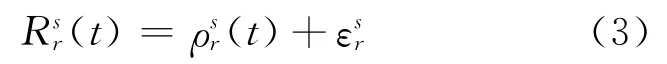
其中，t为观测历元，表示卫星s至测站r的真实几何距离，表示伪距或相位观测量，表示观测模型的所有误差。

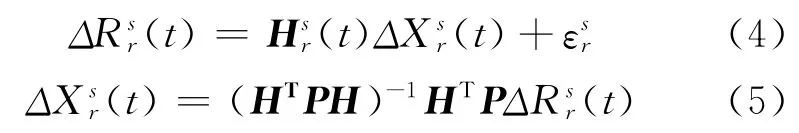
其中，P为权矩阵；H为设计矩阵，即，如式（6）所示：

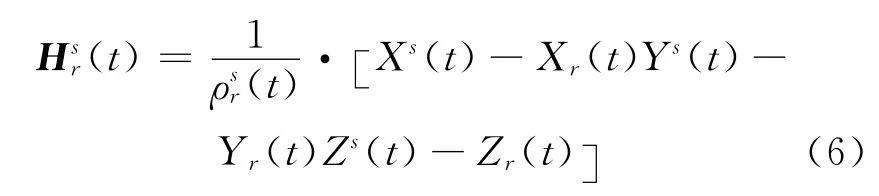
考虑到k个测站时，Hsr（t）如式（7）所示：

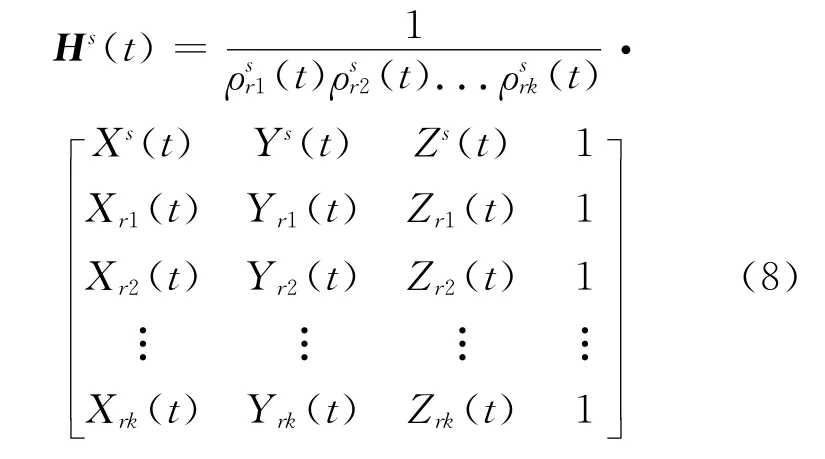
式（7）化简可得式（8）：采用位置精度衰减因子PDOP 来衡量轨道位置的精度，如式（9）所示。因此，只需关注HTPH，为讨论简便，假定P＝I，分析HTH矩阵即可。

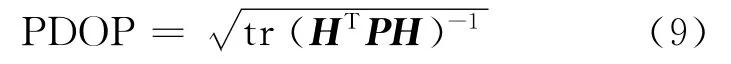
当k＝3时，Hsr（t）的行列式值可化简为：

从式（10）可以看出，当V越大时，｜Hs（t）｜和HTH的值越大，PDOP 值也就越小。同样，当k＝N时，可将观测网分成［N／3］＋1个子网，每个子网Hsr（t）均满足式（10）的性质。进而，根据分网平差与整体平差等价的原理［10］，整网Hsr（t）也满足式（10）的性质，即在保证卫星可见性及测站数据质量的前提下，测站之间的基线越长，地理分布越均匀、越开阔，定轨精度越高。因此，完善的测站选取策略对定轨精度有着重要影响。同时，更少的冗余测站，可以极大提高定轨的计算效率，并保证足够高的定轨精度。

改进后的测站选取策略，兼顾数据质量和测站地理分布，并能根据最大使用测站数合理划分经纬度格网，自动选取最优的测站集合。当最大测站数k＝N时，全球格网经纬度按进行划分，整个测站选取流程如图2所示。其中，数据有效率等于数据预处理前实际观测历元数与数据预处理后有效观测历元数之比。

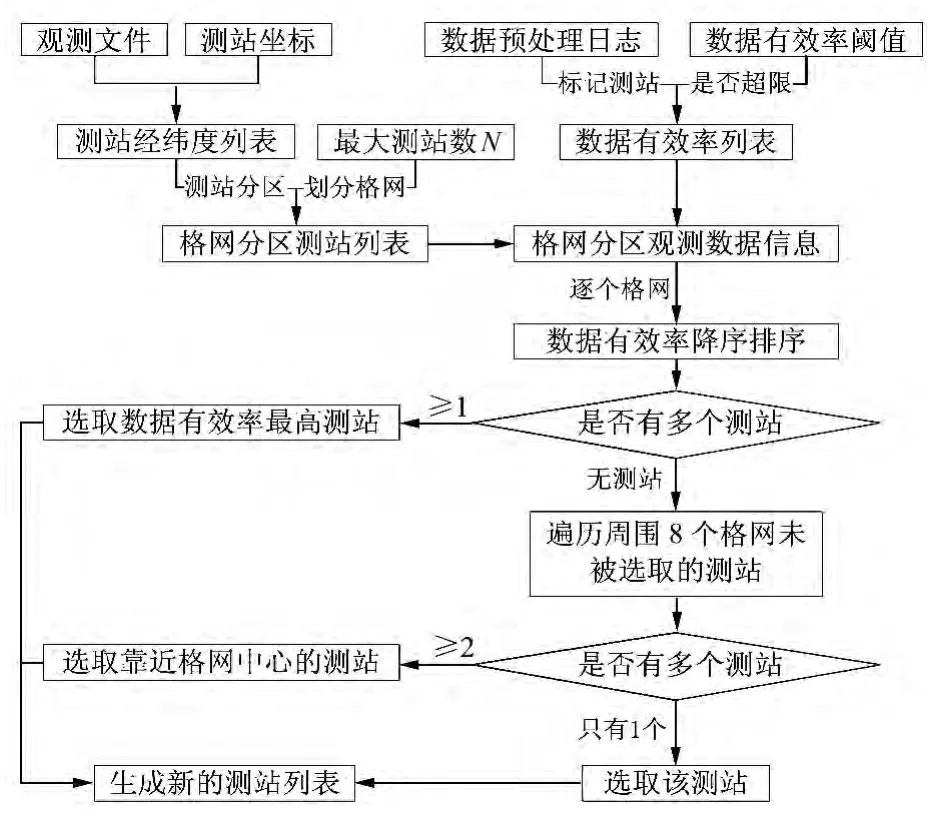
图2 测站选取流程Fig.2 Flow chart of station selection

2 算例分析

观测数据采用IGS 全球观测网和11 个iGMAS跟踪站，时间为2014年121～123d（年积日）。为验证测站选取策略的有效性，设计了3种不同方案，分别选取30、40、50个全球均匀分布的测站进行GPS精密定轨实验。同时，为了对比以上3种方案的定轨精度，也分别选取30、40、50个测站进行定轨实验，但不顾及测站分布，仅按照测站数据质量高低选站。

计算单天弧段解完毕后，又进行了3d弧段的法方程叠加，将得到的3d最终解与IGS最终轨道产品互差，并统计径向、切向、法向以及3D位置偏差的均方根。3d最终解定轨精度统计结果分别如图3～5所示。可以看出，3种方案的定轨精度都具有以下特征：测站均匀分布时的定轨精度明显优于未考虑测站分布时的定轨精度；径向轨道精度明显要优于切向和法向。其中，切向轨道精度最差，这是因为动力学定轨中，切向上的一些摄动力模型难以进一步精化。

图3 方案1最终解统计Fig.3 The final result statistics of scheme 1

从图3可以看出，在测站均匀分布时，方案1在径向、切向、法向位置偏差的均方根分别为2.17、4.63、3.25cm，3D 均方根误差为6.06cm；而未考虑测站分布时，3D 均方根误差为11cm 左右。方案1仅用30个测站，定轨精度就可以达到6cm，说明测站地理分布的合理性。但是，由于使用的测站较少，参数估计时的冗余观测条件较少，不能取得很好的定轨精度。

从图4可以看出，在测站均匀分布时，方案2在径向、切向、法向位置偏差的均方根分别为1.25、2.66、1.87cm，3D 均方根误差为3.48cm；而未考虑测站分布时，3D 均方根误差为8cm 左右。方案2较方案1增加了10个测站，定轨精度就可以达到3.5cm，较方案1定轨精度提高非常显著，说明在测站均匀分布的情况下，增加一定数量的测站可以提高定轨精度。

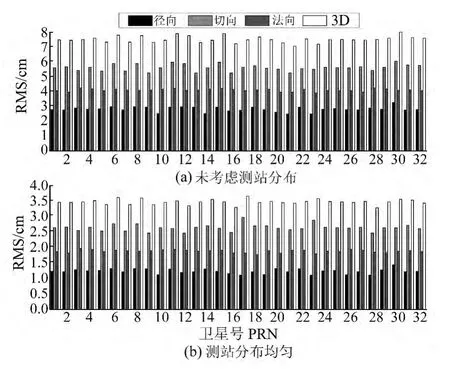
图4 方案2最终解统计Fig.4 The final result statistics of scheme 2

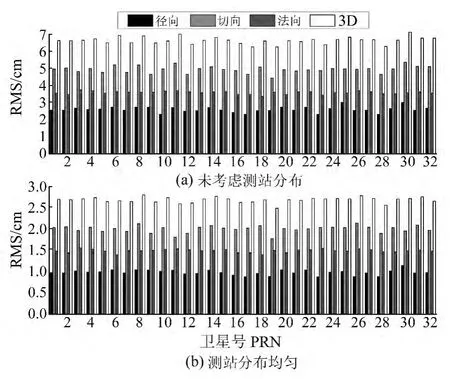
图5 方案3定最终解统计Fig.5 The final result statistics of scheme 3

从图5可以看出，在测站均匀分布时，方案3在径向、切向、法向位置偏差的均方根分别为0.98、2.08、1.50cm，3D 均方根误差为2.75cm。目前IGS最终轨道产品的精度为2.5cm，因此，定轨结果与IGS最终轨道产品精度基本相当。而未考虑测站分布时，3D均方根误差为7cm 左右。方案3较方案2 增加了10个测站，定轨精度可以提高0.73cm。需要说明的是，在200个测站数据全部参与解算的情况下，GPS定轨精度也在2.8cm 左右。因此，基于改进后的测站选取策略，超过50个测站对GPS定轨精度提高基本没有贡献。

同时，表1给出了方案3使用50个均匀分布测站时法方程叠加前后3d解的对比结果。从表1可以看出，法方程叠加后3d解的轨道精度都有0.15cm 左右的提高。这是因为在法方程叠加前，3个单天解都是独立解算的，在单天轨道弧段邻接处是不连续的。在定轨弧段邻接处，采取每12h调节1次伪随机脉冲加速度，进行3d法方程叠加后，可以得到3d连续平滑的轨道。

表1 法方程叠加前后结果统计／cmTab.1 The statistics before and after normal equation stacking／cm

3 结 论

1）在保证卫星可见性及测站数据质量的前提下，测站之间的基线越长，地理分布越均匀、越开阔，定轨精度越高。

2）基于改进后的测站选取策略，选取50个左右的测站，GPS定轨精度可以达到与IGS最终轨道产品精度基本相当的水平。超过50个的测站对GPS定轨精度提高基本没有贡献。

3）改进后的测站选取策略可以自动选取全球均匀分布的测站，避免了手动选取测站的麻烦。同时，也避免了冗余测站参与解算，提高了计算效率，并能达到足够高的定轨精度。

致谢：感谢全球连续监测评估系统（iGMAS）信息工程大学分析中心对本文工作的帮助和支持！

［1］Yunck T P，Wu S C，Wu J T.Strategies for Sub－Decimeter Satellite Tracking with GPS［J］.PLANS’86－Position Location and Navigation Symposium，1986（1）：122－128

［2］Kouba J.A Guide to Using International GNSS Service（IGS）Products［J］.International GNSS，2009，4（3）：106

［3］施闯，赵齐乐，楼益栋，等.卫星导航系统综合分析处理软件PANDA 及研究进展［J］.航天器工程，2009（4）：64－70（Shi Chuang，Zhao Qile，Lou Yidong，et al.PANDA：Comprehensive Processing Software for Satellite Navigation Systems and Its Research Progress［J］.Spacecraft Engineering，2009（4）：64－70）

［4］楼益栋.导航卫星实时精密轨道与钟差确定［D］.武汉：武汉大学，2008（Lou Yidong.Research on Real－Time Precise GPS Orbit and Clock Offset Determination［D］.Wuhan：Wuhan University，2008）

［5］李敏.多模GNSS融合精密定轨理论及其应用研究［D］.武汉：武汉大学，2011（Li Min.Research On Real－Time Precise GPS Orbit and Clock Offset Determination［D］.Wuhan：Wuhan University，2011）

［6］Blewitt G.An Automatic Editing Algorithm for GPS Data［J］.Geophysical Research Letters，1990，17（3）：199－202

［7］潭冰峰，袁运斌，刘腾，等.基于全球IGS 数据分网确定GPS 卫星轨道［J］.大地测量与地球动力学，2014，34（1）：84－87（Tan Bingfeng，Yuan Yunbin，Liu Teng，et al.Precise Orbit Determination of GPS Navigation Constellation Based on Clusters Method Using Global IGS Station Observations［J］.Journal of Geodesy and Geodynamics，2014，34（1）：84－87）

［8］Lichten S M，Border J S.Strategies for High Precision Global Positioning System Orbit Determination［J］.Journal of Geophysical Research：Solid Earth（1978－2012），1987，92（B12）：12 751－12 762