对高中数学教学中实施“ 翻转课堂”的思考

马 睿

（宁夏石嘴山市师资培训中心）

“ 翻转课堂”（The Flipped Classroom）也称“ 颠倒课堂”。2007 年起源于美国佛罗里达州落基山的一个山区学校，随即迅速兴起于美国各地。2010 年左后，中国引入翻转课堂教学理念和模式，因其突破传统课堂局限、满足学生的个性化需求、结合现代信息技术等优势受到教育界的广泛热捧。“ 翻转课堂”在宁夏的发展相对滞后，但也因此更有利于借鉴各地已有的经验，对“ 翻转课堂”做出理性的思考。

一、翻转课堂的实质与内涵

所谓翻转课堂，就是在信息化环境中，课程教师提供以教学视频为主要形式的学习资源，学生在上课前完成对教学视频等学习资源的观看和学习，师生在课堂上一起完成作业答疑、协作探究和互动交流等活动的一种新型的教学模式。

二、传统课堂与翻转课堂教学设计对比

以《函数单调性》为例。

（一）传统课堂教学设计（简案）

1.创设情境，引入课题

实例：观察课件中2008 年8 月8 日（北京奥运会开幕式举办）一天24 小时内气温随时间变化的曲线图，请你根据曲线图说说气温的变化情况？

问题1：观察下列函数图象，请你说说这些函数有什么变化趋势？

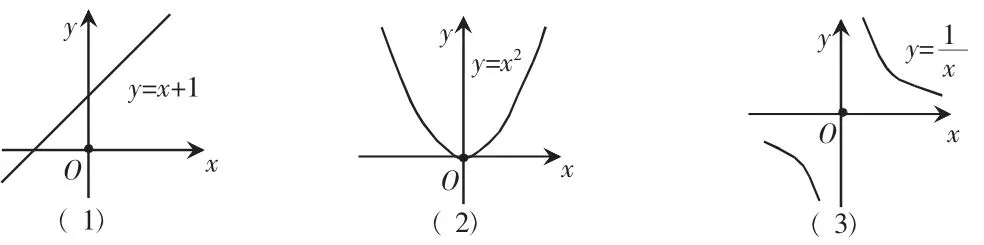
2.引导探索，生成概念

问题3：（1）以二次函数f（x）=x2在区间上［0，＋∞）的单调性为例，如何用数学符号描述函数图象的“ 上升”特征，即y 随x 的增大而增大”？

利用几何画板在函数图象上任找一点，当点在函数图象上“ 按横坐标（即自变量）增大”的方向移动时，观察点的纵坐标（即函数值）的变化规律，让学生思考、讨论得出，若x1＜x2，则必须有y1＜y2）在几何画板中作出二次函数f（x）=x2图象，回答下列问题：

（2）已知a＜x1＜x2＜b，若有f（a）＜f（x1）＜f（x2）＜f（b）能保证函数在区间上递增吗？

（3）已知a＜x1＜x2＜x3＜b，若有f（a）＜f（x1）＜f（x2）＜f（x3）＜f（b），能保证函数在区间上递增吗？

（4）已知a＜x1＜x2＜＜x3＜x4…＜b，

若有f（a）＜f（x1）＜f（x2）＜f（x3）＜f（x4）…＜f（b）能保证函数在区间上递增吗？

问题4：如何用数学语言准确刻画函数y=f（x）在区间D 上递增呢？ 请你试着用数学语言定义函数y=f（x）在区间D 上是递减的。

3.学以致用，理解感悟

例1：判断题

（二）翻转课堂教学设计（简案）

1.课前任务设计

（1）观察2008 年8 月8 日（北京奥运会开幕式举办）一天24小时内气温随时间变化的曲线图，体会在某些时段气温升高，某些时段气温降低。

（2）从网络中搜集一些生活中的例子（如股票的盈亏），观察所搜实例的曲线图中自变量变化时，函数值的大小是如何变化的？体会函数在不同区间上的变化差异，将结果和同学分享。

（3）自学1.3.1 函数的单调性完成下列任务：

①给出函数单调性的数学语言。

②概括证明函数单调性的步骤。

③完成课本上第30 页的探究。

④完成练习中第32 页的2、3、4 题，上传给教师。

⑤记录下学习中的疑问、困惑上传给教师。

2.课上任务设计

（1）小组讨论已搜集生活实例以及对函数单调性数学语言的理解。请小组代表上台展示精选实例，描述函数值的大小是如何随自变量的变化而变化的，并用自己的语言给出函数单调性的定义。

（2）练习以下题目：

③函数f（x）=x2+ax 在（-1，+∞）是增函数，那么a 的取值范围是？

（3）小组讨论展示自己总结的函数单调性的证明方法与步骤，小组代表上台讲解，教师给予补充总结。

（4）练习以下题目，课本第39 页A 组2、3；B 组1（1）。

（5）总结：学生发言学到了什么？ 什么地方还有疑问？ 还想学什么？

三、翻转课堂实践中的思考

1.以上两个教学设计均从现实情景出发，让学生直观感受气温的变化，从实际问题中抽象出函数的模型。翻转课堂的教学设计更是利用网络资源，让学生体会到数学与实际问题息息相关。但如何从实际问题中抽象出数学模型，对高中数学的学习是一个难点，教学中应注意对这个问题进行引导。传统课堂中，教师用引导性的语言，如“ 函数是表达现实世界中数量之间变化规律的一种数学模型”等语言，引导学生将气温变化的直观认识过渡到函数的增减，有效培养了学生的数学思维。翻转课堂中对学生在此处能力的要求较高，以至很多学生直接忽略了此点。

2.函数单调性这一节课有两个认知冲突，一是利用函数图象可以直观判断出函数的单调性，为什么要学习数学符号语言？二是如何通过研究特殊函数的单调性归纳出一般的函数单调性的定义。

对第一点，传统课堂教学设计利用有些函数单从图象无法精确得到单调区间的知识障碍，让学生体会数形结合思想，自主体验学习新知的必要性。对第二点，抓住新旧知识间的内在联系，设置一系列问题，让学生充分参与定义的符号化过程，有效地突破了教学难点。而在翻转课堂中，由于利用微视频授课的局限性，缺少教师和学生之间思维的碰撞，概念的形成也缺少过程性。即便在微视频中也利用问题串的形式，但由于学生观看视频时习惯一味地观看而缺乏思考，往往会忽视过程，只重结果。

3.较传统课堂设计的三道题目而言，翻转课堂中由于学生有了前置学习和基础练习，所以课堂上有更多的精力总结、提高，且能给予学生更多的展示结果的机会，因此，更有利于发展学生的发散思维，享受成功的喜悦。但笔者认为针对不同程度的学生，利用课本上的题目培养学生对概念理解的严谨性，也是非常必要的，在题目的解答过程中，有时也要发挥好教师的示范功能。

综上所述，为发展学生数学思维，提高数学素养，在数学课堂教学中应注重问题的提出、概念的形成、数学思想方法的体验都需由学生亲历，切勿让多媒体资源和设备代替了学生的思维过程。翻转课堂和传统课堂在教育功能上各有优势，翻转课堂的实践要注意适时性、合理性，在融合传统课堂教学模式优势的基础上进一步发展，方能设计出完美的翻转课堂。

钟晓流，宋述强，焦丽珍.信息化环境中基于翻转课堂理念的教学设计研究［J］.开放教育研究，2013（02）：58-63.