立式储罐基础沉降与变形后的可靠度评价
2015-02-15赵楠楠大庆油田设计院
赵楠楠 大庆油田设计院
立式储罐基础沉降与变形后的可靠度评价
赵楠楠 大庆油田设计院
针对基础沉降和变形后的立式储罐,采用大型有限元软件进行分析,对储罐地基的沉降过程进行仿真,并且对储罐的可靠度进行分析研究。运用有限元模型,分析地基土体的渗透系数、压缩模量、加载天数和泊松比等因素对沉降和变形的影响,以及孔隙压力的变化。用验算点的超平面代替极限状态曲面进行分析,没有考虑到极限状态曲面的凸凹性,当极限状态方程的非线性程度较高时,误差非常大。随机数初始值的改变对失效概率有影响,但是通过增加抽样次数,可以减小这种影响,使所得到的失效概率满足工程的需要。
立式储罐;地基沉降;底板应力;底板沉降;可靠度
立式储罐是输油系统中的重要生产设备,其内多储存易燃易爆、具有对环境产生污染的介质,一旦发生安全事故将造成严重的经济损失,并对生态环境造成严重的破坏。针对基础沉降和变形后的立式储罐,采用大型有限元软件进行分析,对储罐地基的沉降过程进行仿真,并且对储罐的可靠度进行分析研究。
1 可靠度评价内容与方法
针对立式储罐基础沉降和变形的特点,进行可靠度评价研究。
运用ADINA有限元分析软件建立有限元模型。地基单元选用三维实体单元(3—D solid);储罐底板单元选用壳单元;接触单元选用接触面(contactor surface)和目标面(target surface)共同建立接触对。
(1)采用大型有限元软件,对储罐地基的沉降过程进行了数值模拟,分析地基土体的渗透系数、压缩模量、加载天数和泊松比等因素对沉降和变形的影响,以及孔隙压力的变化[1]。同时,分析地基在欠固结情况下储罐的沉降过程。
(2)分析储罐底板的变形和沉降量,以及储罐底板的径向应力和环向应力。储罐底板的径向应力在靠近底板边缘和中心位置出现了最大拉应力,储罐底板的环向应力值没有明显的变化。
(3)根据储罐的沉降量,建立储罐的功能函数,采用改进的一次二阶矩法和蒙特卡罗法求解储罐的可靠度,并且对这两种方法的分析结果进行对比分析。
2 地基沉降分析
(1)渗透系数不影响地基沉降的最终沉降量,对于同一压缩模量的地基,土体渗透性越小,地基的沉降越缓慢;土体的渗透系数对软地基的影响大。
(2)对于压缩模量大的地基,在加载期间,地基沉降可以认为是线性的,而且固结沉降和次固结沉降的时间比较短[2]。
(3)加载速度不影响地基沉降的最终沉降量。
(4)泊松比影响地基的最终沉降量,地基的压缩模量一定时,泊松比越大,地基的最终沉降量越小。
(5)压缩模量影响地基的最终沉降量,地基的压缩模量越大,地基最终沉降量越小。
(6)在相同荷载作用下,压缩模量越大,土体的有效应力就越大,孔隙压力就越小。
3 底板变形及应力分析
不同底板坡度的储罐,地基弹性模量为5E6Pa、 1E7Pa、和2E7Pa时,对由于地基沉降引起储罐底板的变形、沉降量、径向应力、环向应力进行有限元分析[3],得出以下结论:
(1)随着储罐底板坡度增加,底板的变形加大,底板要承受较大的变形。
(2)储罐底板的最大、最终沉降量不是在储罐底板的中心位置,这是因为储罐底板在设计时有坡度,在底板的中心形成圆锥,从而提高了中心的刚度,导致中心的沉降量受到了影响。
(3)储罐底板的径向应力在边缘处和中心处出现了应力的极值,在边缘处的径向应力为最大值,其他位置的径向应力曲线平缓。
(4)储罐底板的环向应力变化不明显。随着储罐底板向下起锥面的坡度加大,位于底板边缘附近出现了最大值,所以在这个位置径向应力也出现了最大值,容易出现三向受拉的情况,导致储罐底板的脆性破坏。
(5)地基正常固结和欠固结情况相比,储罐底板的变形形状相似,沉降量增加幅度大。所以在设计时要特别注意地基土体的欠固结情况。
4 可靠度分析
用一次二阶矩法求储罐底板的可靠度,在设计验算点p∗(h∗,γ∗,B∗,E∗)将功能函数进行Taylor基数展开,仅保留线性项,有

而可靠性指标表示为
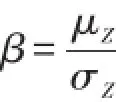
设计验算点的坐标为

改进的一次二阶矩法的计算步骤:①假定p∗(设h∗=μh,γ∗=μγ,B∗=μB,E∗=μE);②求cosθh,cosθγ,cosθB,cosθE;③求β;④求新的p∗;⑤以新的p∗重复步骤②~④,直到最后两次算出的β值之差小于允许误差。
将采用改进的一次二阶矩法计算的失效概率和采用蒙特卡罗法计算的失效概率对比可得,两者的结果相差很多,有的相差几个数量级。但是在多数情况下,能够得到比较好的结果。这是因为改进的一次二阶矩法在计算可靠度时,对功能函数在验算点展开成Taylor基数,保留一次项。用验算点的超平面代替极限状态曲面进行分析,没有考虑到极限状态曲面的凸凹性,当极限状态方程的非线性程度较高时,误差非常大。随机数初始值的改变对失效概率有影响,但是通过增加抽样次数,可以减小这种影响,使所得到的失效概率满足工程的需要。
[1]孙建刚,王振,袁朝庆.储罐隔震设计简化分析方法[J].地震工程与工程振动,2001,21(2):157~160.
[2]孙建刚,郝进锋.储液罐液-固耦联振动固有特性有限元分析[J].大庆石油学院学报,1998,22(3):96~100.
[3]孙建刚,张丽,袁朝庆.立式储罐基础隔震动力反应特性分析[J].地震工程与工程振动,2001,21(3):140~144.
(栏目主持杨军)
10.3969/j.issn.1006-6896.2015.5.007
