基于流-热耦合模型的土石坝渗流热监测研究

吴志伟，宋汉周

（1.河海大学 地球科学与工程学院，江苏 南京 210098；2.东北电力设计院，吉林 长春 130033）

1 引言

渗流监测一直是土石坝安全监测的重要内容之一。通过监测土石坝渗流状态，能够预测渗流发展趋势、估算渗漏量、探查渗流异常部位、评价土石坝的运行状况。根据观测资料分析结果，拟定除险加固措施，保证土石坝的安全运行。常规的土石坝渗流监测技术包括渗透压力观测和渗流量观测[1]，此外，还可以采用一些辅助手段，如电法、天然及人工同位素示踪法、热监测技术等。

通过温度测量确定土石坝渗流性状的研究偶见报道，特别是近年来发展起来的分布式光纤测温技术（distributed fiber optic temperature sensor system，简称DTS），给土石坝热监测提供了有利的技术手段，克服了点式温度传感器测量坝体温度场的不足[2－3]。分布式光纤测温系统快速商品化，其性能指标也在逐渐提高，温度测量精度与传统温度计一致，空间分辨率已小于1 m，且光纤铠装使其能够适应复杂的外部环境。分布式光纤测温系统作为一种先进的测温手段，其环境适应能力、耐久性和测量精度均能满足土石坝温度场监测的基本要求。国内在景洪水电站[4]、长调水电站[5]、西龙池水库[6]等水电工程中都有相关应用报道。测量渗漏发生前后的温度差异来定位渗漏发生的位置，集中渗漏会引起坝体局部的温度场分布改变，通过对光纤周围介质温度场的分析，可以确定坝体发生渗漏的部位。而且基于分布式光纤传感技术的温度测量资料，能够用来计算渗流流速，文献[7]在此方面开展了一些尝试性的理论和试验研究。

土石坝热监测技术的理论基础是岩土体中渗流场与温度场（流-热）的耦合作用，介质中的水分运移控制着温度场的分布，反之，温度场的时空分布能反演渗流场特征。对于土石坝，坝体浸润线以上的非饱和带占有重要的比例，非饱和渗流影响着热量传递过程，土石坝渗流热监测的背景温度场是与大气温度相关的周期性波动温度场。理论上，分布式光纤热传感器可以测试得到研究对象的温度时空分布特征，该温度资料受多种因素影响，特别是周期性波动气温的影响。为了提取反映库水渗漏所引起的温度场响应特征，有必要深入研究运行期坝体温度场的特征，而现有研究还多是基于经验的定性分析[8]。

本文根据土石坝温度场的基本特征，建立土石坝饱和-非饱和渗流场与温度场耦合数学模型。以典型二维心墙土石坝渗流场与温度场数值模拟作为算例，模拟天然条件下此类坝的坝体渗流场和瞬态温度场特征，并模拟库水集中渗漏情形下该瞬态温度场的响应。其成果可为土石坝渗流热监测技术的应用提供参考。

2 数学模型

土石坝饱和-非饱和瞬态渗流场采用Richards方程描述：

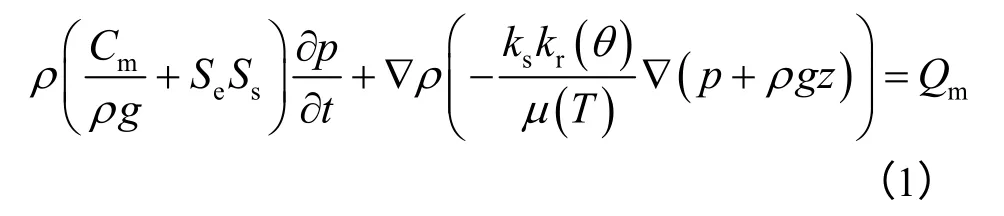
式中：p为压强；g为重力加速度；ρ为水的密度，这里假设为常量；μ（T）为水的动力黏度，μ（T）=0.000 024 14 ×10（247.8/（T+133.16）），为温度T 的函数；z为计算点位置高程；θ为含水率，在饱和带其数值等于孔隙度；Cm为容水度，是水分特征曲线斜率的负倒数；Se为土壤的相对饱和度；ks为介质饱和渗透率；kr（θ）为非饱和带相对渗透率（0≤kr（θ）≤1），是含水率θ 的函数；Ss为弹性贮水率；Qm为水流源汇项；▽为拉普拉斯算子。

温度场采用热对流传热方程[9]描述：

式中：T为地下水温度；λeq为等效导热系数；ceq为等效比热容；ρeq为等效密度；cw为水的比热容；ρw为水的密度；Qs为热量源汇项；u为水的平均流速，在数值上u=v /θ。

式中：DH为水动力弥散系数；αT为横向弥散度；αL为纵向弥散度；vi为i 方向流速矢量；δij为克里格常量，当i=j时为1，否则为0；为流速矢量的大小。

非饱和带土壤水分特征曲线采用Van Genuchten 模型[10]（简称VG 模型）来描述：

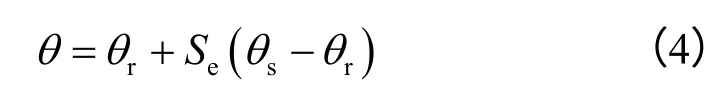
式中：Se为土壤相对饱和度；θr为残余含水率；θs为饱和含水率。其中 Se为

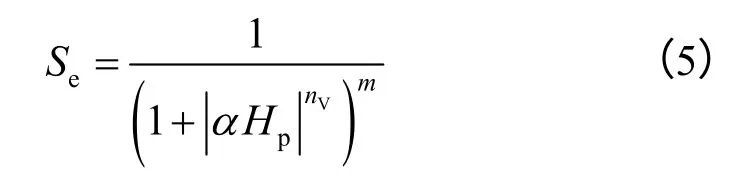
式中：Hp为压力水头，Hp=pw/rw，在非饱和带等于负压水头Hc，其中，pw为压强，rw为水的重度；α、nV、m为VG 模型参数，α为水分特征曲线进气值的倒数，nV为水分特征曲线坡度的指示参数，也是反映土壤孔隙分布的参数，通过拟合土壤水分特征曲线得到，m=1-1/nV。土壤容水度Cm和相对渗透率 kr分别采用下述经验公式表示：

岩土体的等效热参数遵循体积平均定律，即

式中：下标s为固体颗粒，w为水，g为空气；n为多孔介质的孔隙度，若孔隙处于饱和状态，则θ=n，方程退化为饱和含水层对流传热方程。

由于土体饱和状态的导热系数与干燥状态的导热系数差异巨大，非饱和岩土体的等效导热系数eqλ采用Lu 模型[11]确定。由饱和-非饱和渗流场模型得到计算区域的含水率分布状态，由此确定非均质的参数空间分布。Lu 模型主要参数如下：

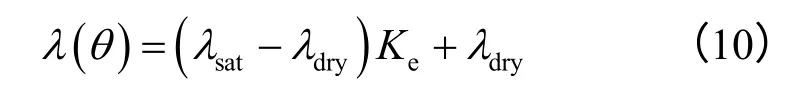
式中：λsat为饱和土体导热系数；λdry为干燥土体导热系数；Ke为插值系数。

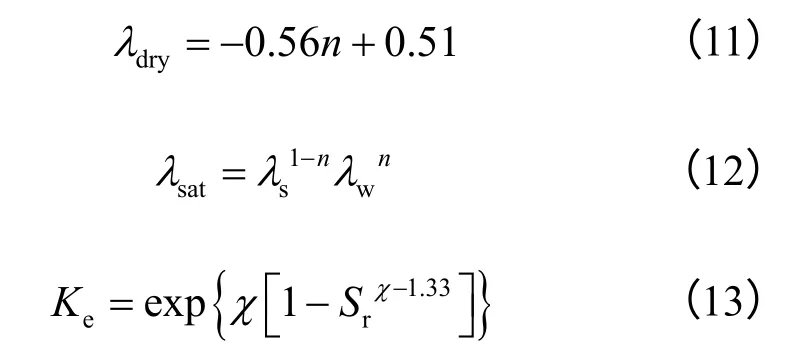
式中：λs为土壤介质的导热系数，由石英含量（q）及其导热系数（λq=7.7 W/(m·℃)）和其他矿物的导热系数（λ0）得到，即，其中：λ0=2.0 W/(m·℃)（q ＞0.2）；λ0=3.0 W/(m·℃)（q≤0.2）；Sr为饱和度；χ 对于砂土、壤土、黏土分别为1.05、0.9、0.58。常数1.33为形状参数。

地表温度随时间周期性变化规律的傅里叶级数函数[12]为

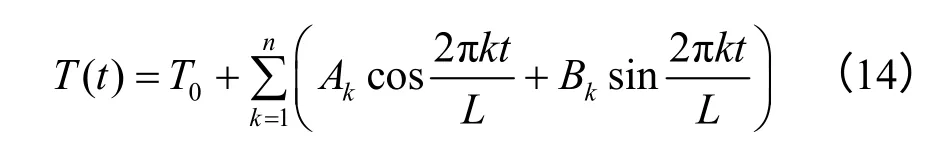
式中：T0为周期内的平均地表温度；k为傅里叶级数的阶数；Ak和 Bk为有限傅里叶级数的系数；L为时间周期，也称第一谐波周期，如一天或一年。

上述模型比较真实地反映了土石坝所处的热-流状态，主要体现在：（1）考虑了温度场的对流传热过程；（2）考虑了非饱和带对渗流和传热过程的影响；（3）非饱和带传热参数是非均质的；（4）考虑了周期性波动气温的影响。该模型是强耦合过程，求解采用COMSOL Mutiphsic 软件，通过修改相关模块，能够实现饱和-非饱和渗流场与温度场耦合模型的有限元求解。

3 某土石坝双场耦合数值模拟

3.1 模型设定

基于上述数值模型，通过数值试验，说明土石坝饱和-非饱和瞬态渗流场与温度场耦合特征。

3.1.1 几何模型

采用的典型土石坝剖面参照湖北大山背水库土石坝[13]坝体给出，并做适当改动，使其具有普遍性。该心墙土石坝坝体结构如图1 所示，坝顶宽为7 m，坝顶高程为108.12 m，坝高为23.2 m，坝体填筑材料假设为粉质黏土；心墙顶高程为106.32 m，顶宽2.0 m，坡度均为1:0.15，心墙材料为黏土。坝体上游坡度为1:2.25，下游坡度为1:2.0；坝体排水体采用褥垫式水平排水，排水褥垫层高为2 m，宽为30 m，排水体的材料为砾石。

为说明集中渗漏对坝体温度场的影响，假设心墙在某时刻形成0.02 m 宽的微细水平裂纹，该心墙裂纹距坝底10.08 m，其渗透特性参照排水褥垫层给出。

图1 心墙土石坝几何模型Fig.1 Geometric model of a clay core embankment dam

3.1.2 计算参数

参照相关文献，给出计算模型的渗流场及温度场计算参数，如表1 所示。其中，非饱和渗流参数参照文献[14－16]给出，其他渗流场参数及温度场参数取经验值。热弥散度均取0.01 m；空气和水的热传导系数分别取0.024 W/(m·℃)和0.58 W/(m·℃)；空气和水的质量热容分别取1 005 J/(kg·℃)和4 186 J/(kg·℃)；空气和水的密度分别取1.205 kg/m3和1 000 kg/m3。

3.1.3 边界条件与初始条件

对于饱和-非饱和渗流场，上游坝体A-B-C为定水头边界，水头为104.92 m；下游D-E 边界为定水头边界，水头为86.92 m；其他边界为零通量边界。

对于温度场，A-B 边界取为定温度边界，参照文献[17]，按华中地区水库平均水温10℃取值；底部边界E-A为绝热边界；B-C-D-E 边界与大气接触，具有季节波动，按日平均气温取值。这里采用该地区气温散点资料（资料来源：中国气象科学数据共享服务网），由式（14）拟合得到该地年气温波动模型。取5 阶傅立叶级数就可以满足精度要求，该地年气温回归模型系数分别为：T0=17.737 2、A1=-12.053 7、B1=-3.703 7、A2=-1.231 0、B2=-0.291 5、A3=-0.272 1、B3=-0.486 5、A4=-0.049 7、B4=0.252 0、A5=-0.105 2、B5=-0.180 8。因此，得到年平均气温为17.74℃，采用此模型可以确定各时刻的气温波动。

表1 土石坝瞬态传热模型计算参数Table 1 Parameters of transient heat transfer simulation

渗流场初始条件假设压力水头为0，温度场假设初始温度为年平均气温。

3.1.4 计算工况与时间离散

首先，计算瞬态温度场，模拟蓄水之后饱和-非饱和渗流及其对温度场的影响，评价土石坝温度场的季节波动特征；然后，假设土石坝心墙形成缺陷，发生集中渗漏，通过数值模型，分析该集中渗漏对土石坝渗流场及温度场的影响。

基于上述工况假设，设置第1个计算时间区段为6 a（2 190 d），之后发生集中渗漏，集中渗漏计算时间为200 d，取时间步长为1 d。

3.2 模型计算结果与分析

3.2.1 坝体饱和-非饱和渗流场

各时段坝体渗流场压力水头分布如图2 所示。黏土心墙防渗体的渗透性极低，等压线密集，地下水渗流流速十分缓慢，坝体浸润线（图中零压力线）穿过心墙后急剧降低。心墙前坝体在库水的作用下，其压力水头为水平状分布。坝体浸润线以上形成非饱和带，非饱和带主要分布在心墙后的下游坝体。非饱和带饱和度由坝体浸润线至坝体外表面逐渐减小，在基质吸力的作用下，存在部分地下水越过坝体浸润线运移至非饱和带。

由图2 可知，坝体浸润线与排水褥垫层的上表面高程基本一致，说明穿越心墙的库水主要通过排水褥垫层排出坝体，单宽排水量约为0.36 m3/d。因此，在常规土石坝坝身构造条件下，心墙能有效降低坝体浸润线，穿越心墙的水量较小，而这部分渗漏库水能通过排水褥垫层排出，心墙防渗体和排水褥垫层排水体能有效保证土石坝的运行安全。

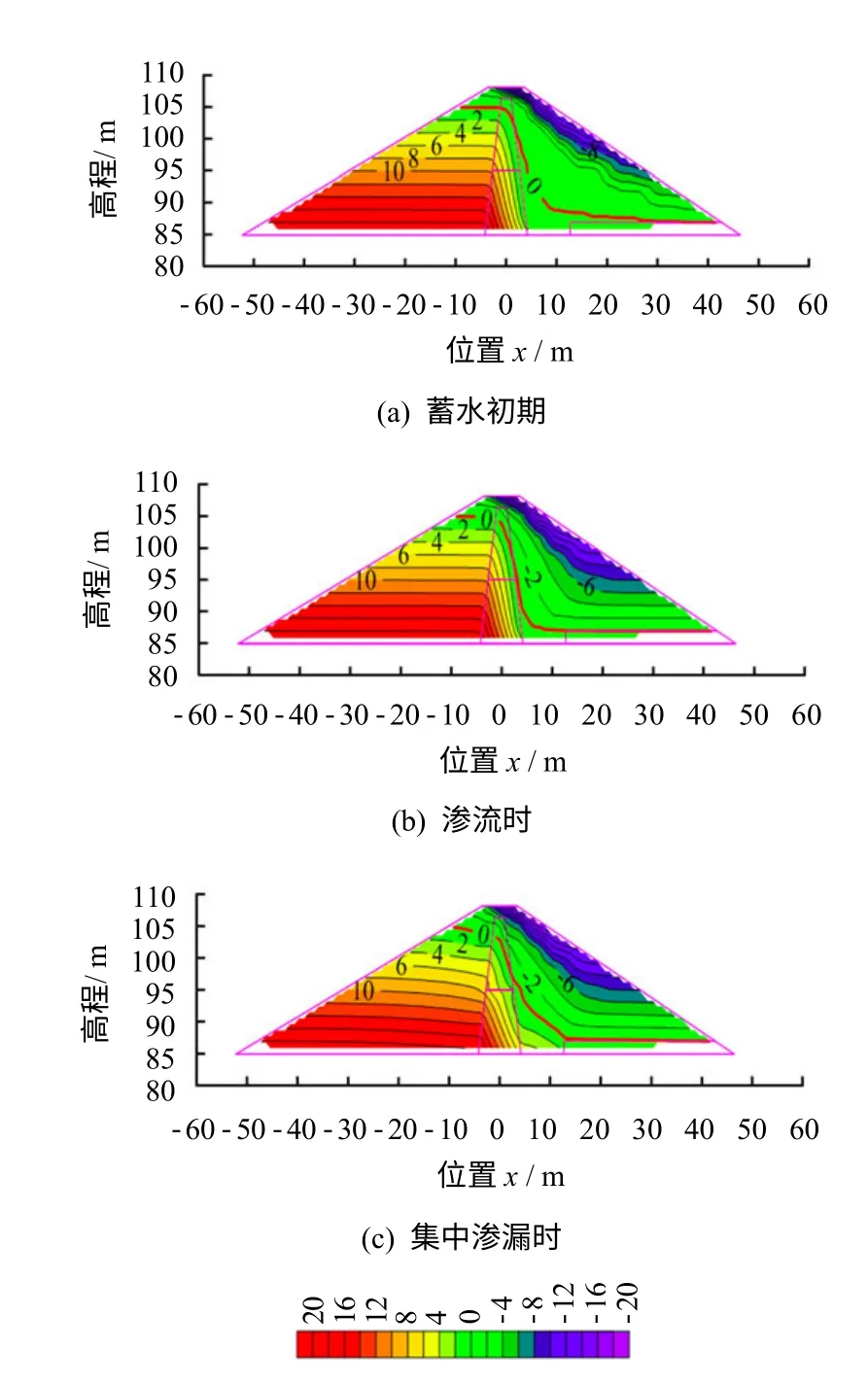
图2 不同时刻坝体压力水头分布图Fig.2 Pressure head distributions along profile at different times

各时段坝体压力水头分布不尽相同，由于假定计算开始时坝前库水即达到最大库水位，那么蓄水初期心墙后坝体浸润线（见图2(a)）略高于渗流稳定时的状态。渗流稳定时，坝体浸润线如图2(b)所示，穿过心墙后急剧降低，下游浸润线的高程与排水褥垫层基本相同。而心墙发生集中渗漏之后，集中渗漏的单宽渗漏量约为8.3 m3/d，渗漏的库水在心墙后聚集，坝体浸润线明显升高，使部分非饱和带转化为饱和带，如图2(c)所示。

3.2.2 坝体瞬态温度场季节波动

水库蓄水后，温度较低的库水在坝体内部形成稳定渗流，对流传热作用影响着坝体温度场。模型计算结果能得到渗流传热稳定之后的坝体温度场季节波动，这里给出一年中夏季、秋季、冬季典型时刻的坝体温度场分布，如图3 所示。其中夏季为日均气温最高的时刻，秋季为日均气温等于年平均温度的时刻，冬季为日均气温最低的时刻。

图3 坝体温度场季节波动Fig.3 Temperature distributions at different seasons

根据图3 可把坝体温度场分为季节波动特征不同的两个区域：心墙上游受低温库水影响，坝体温度与库水温度基本一致，在10℃左右，且季节变化不明显；心墙下游的非饱和带温度场受气温影响较为显著，且热传递过程受非饱和土体的阻滞，坝体内部温度的季节波动小于坝体表面，坝体内部温度波动范围约在11℃～15℃。背水坡面下部6 m以浅的范围内，温度的季节波动特征最为显著。在时间域上，当日均气温高于10℃时，如夏季与秋季，由背水坡面到坝体内部温度逐渐降低，而夏季温度梯度较大，等温线较密集，秋季温度梯度较小，等温线较稀疏。冬季气温降低，在坝体内部形成逆温区，坝体内部温度高于坝体表面。

综上所述，低矮土石坝等挡水建筑物的温度场受坝体渗流和气温的影响，库水及气温是两个重要热源，饱和带的温度受库水渗流控制，非饱和带主要受气温控制，具有季节波动特征。可见在开展土石坝热监测、温度示踪等方法研究时，应考虑坝体温度场的季节波动。

4 集中渗漏条件下瞬态温度场的响应

土石坝热监测技术可观测其温度场是否存在时空分布异常，温度示踪探测技术是通过测温查明土石坝是否存在集中渗漏，上述方法均假设土石坝的异常渗漏导致坝体温度场发生改变。为说明集中渗漏条件下坝体温度场的响应，假设心墙发生集中渗漏，渗漏部位距坝底10.08 m，计算时长为200 d，时间步长为1 d，由此得到集中渗漏条件下坝体温度场的畸变。

同一时刻无集中渗漏和发生集中渗漏的坝体温度场对比如图4 所示。无集中渗漏时（见图4(a)），坝体温度场由心墙前库水的低温区逐渐过渡到坝体表面的高温区，等温线较为均一；而发生集中渗漏后（见图4(b)），心墙前库水通过集中渗漏带渗漏进入非饱和带，将温度较高的表层库水带入集中渗漏带，心墙前形成等温线较密集的温度突变带，越过集中渗漏带的低温库水使心墙后坝体温度降低，气温影响深度相应地变小。

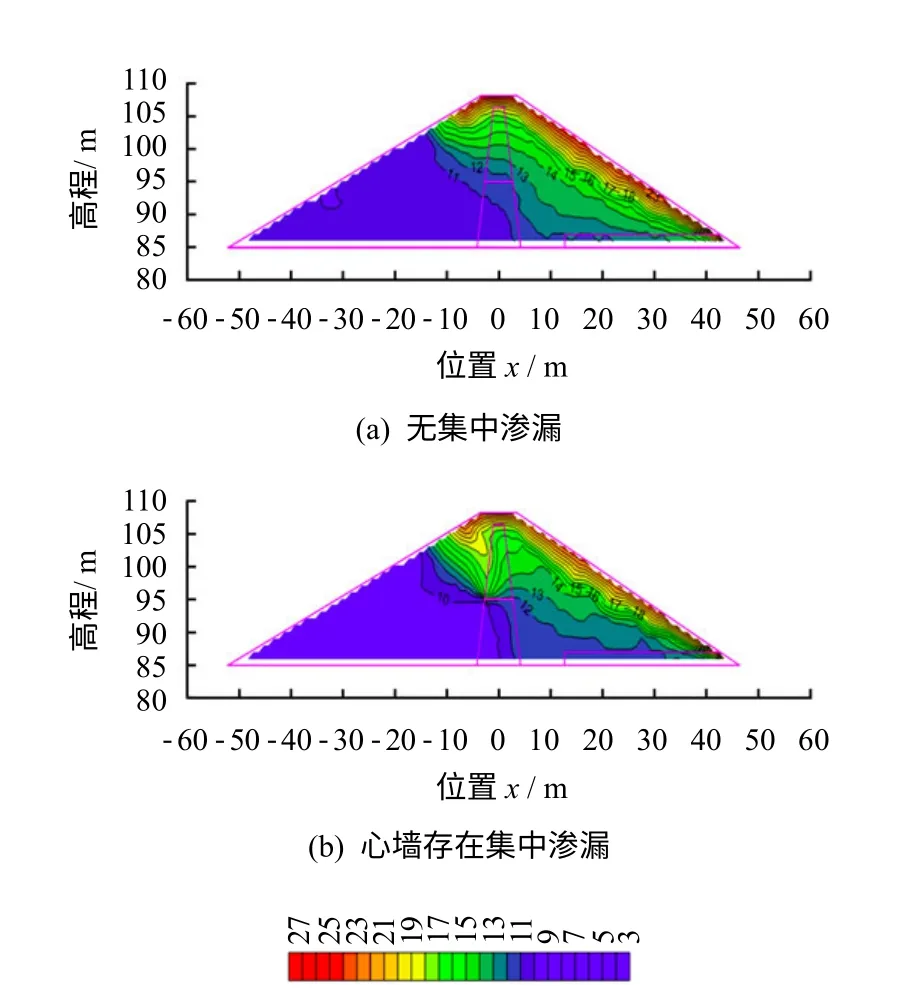
图4 集中渗漏对坝体温度场的影响Fig.4 Temperature field of dam influenced by concentrated leakage

因此，集中渗漏将使低温库水主要通过集中渗漏带流入下游，低温库水所经过的路径范围内，通过对流传热改变周围温度场的空间分布。土石坝测温资料所表现出的温度时空分布在一定程度上受集中渗漏的影响，可以通过测温来反演渗流场。

心墙集中渗漏带出口处的流速及温度时序曲线（如图5 所示）反映出在计算时刻2 191 d，开始发生集中渗漏，流速增大到1.33×10-3m/s。在集中渗漏之前，出口处心墙的温度小幅波动；而发生集中渗漏后，该点温度发生突变，骤然降低，经过40 d左右，其温度与库水水温基本一致；而后受气温影响，该点温度逐渐增大。由此可见，温度时序数据的突变点能有效指示发生集中渗漏的时间，温度场对集中渗漏的响应较为敏感。

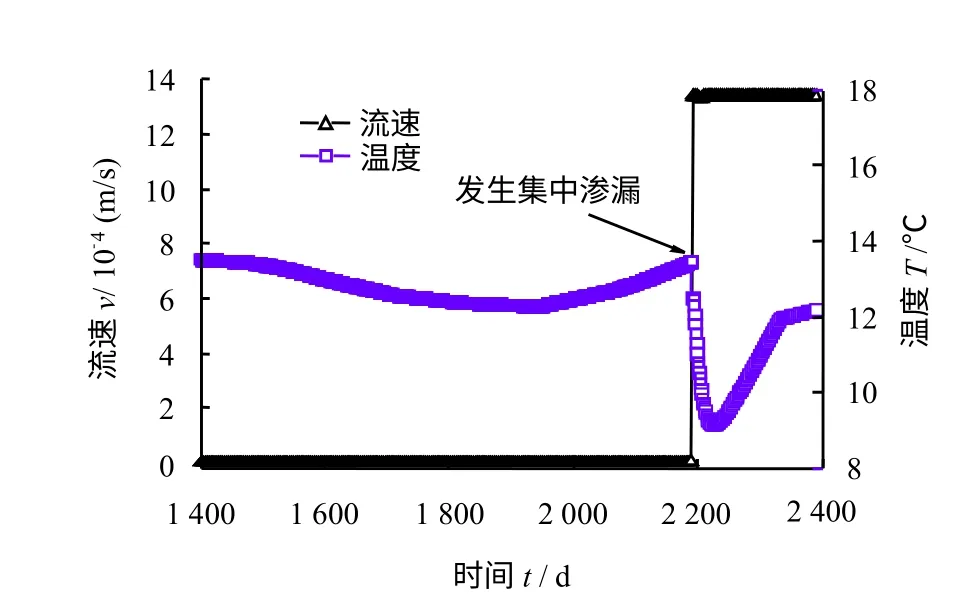
图5 心墙裂纹处流速及温度时序曲线Fig.5 Curves of leakage velocity and temperature time series near core crack

若假设在心墙下游坡面敷设分布式光纤测温传感器，就可以实时测量心墙的温度分布，集中渗漏发生之后不同时刻心墙下游坡面的温度曲线如图6所示。集中渗漏带附近的坝体温度在渗漏发生之后1 d 即显著降低，并在随后的数天内仍降低，但降幅变小。由于分布式光纤测温传感器能精确定位测点位置，那么利用该曲线能有效确定渗漏发生的部位，从而评价坝体渗漏部位的时空分布。

综上，当土石坝发生集中渗漏时，坝体渗流场的改变会引起坝体温度场的改变，温度场的时空分布能够作为渗流场特征的表征。假若采用温度传感器，特别是分布式光纤测温传感器来测量坝体温度场分布时，测量结果能用来分析渗漏部位，确定渗漏发生的时空分布。

图6 集中渗漏时心墙下游坡面温度曲线Fig.6 Curves of temperature distributions along core wall while leaking

5 结论

（1）建立了土石坝饱和-非饱和瞬态渗流场与温度场（流-热）耦合模型，考虑了热对流、热传导和热扩散效应，温度边界按周期性气温考虑，且相关参数按非线性考虑，如流体黏度的热效应、导热系数与含水率相关等。其模型假设与边界条件更加接近真实情况，仿真结果更接近土石坝温度场的真实状态。

（2）以典型二维心墙土石坝渗流场与温度场耦合数值模拟作为算例，计算结果表明：温度场受坝体渗流和气温的共同影响，库水及气温是两个重要热源，饱和带的温度受库水渗流控制，非饱和带主要受气温控制，具有季节波动特征。

（3）数值模拟结果还表明：若土石坝心墙发生集中渗漏，渗漏通道附近岩土体的温度主要受库水影响；若在心墙上敷设分布式光纤传感器，很容易捕捉到渗漏点位置及渗漏发生的时刻。因此，采用渗流热监测技术在理论上可以反映渗流场的时空分布特征。

（4）本文采用数值模拟技术从理论上说明了分布式光纤测温方法的优越性，而该技术的应用研究还处在起步阶段，需加强理论模型、敷设技术、信息化管理和资料处理等方面的研究。

[1]宋汉周.大坝环境水文地质研究[M].北京:中国水利水电出版社,2007.

[2]肖衡林,鲍华,王翠英,等.基于分布式光纤传感器技术的渗流监测理论研究[J].岩土力学,2008,29(10):2794－2798.XIAO Heng-lin,BAO Hua,WANG Cui-ying,et al.Research on theory of seepage monitoring based on distributed optical fiber sensing technology[J].Rock and Soil Mechanics,2008,29(10):2794－2798.

[3]陈江,张少杰,闵兴鑫,等.热脉冲法监测集中渗漏的模型试验[J].岩土力学,2010,31(9):2729－2735.CHEN Jiang,ZHANG Shao-jie,MING Xing-xin,et al.Model experiment for concentrated leakage monitoring by heat pulse method[J].Rock and Soil Mechanics,2010,31(9):2729－2735.

[4]徐卫军,侯建国,李端有.分布式光纤测温系统在景洪电站大坝混凝土温度监测中的应用研究[J].水力发电学报,2007,26(1):97－101.XU Wei-jun,HOU Jian-guo,LI Duan-you.Application research on temperature monitoring in concrete of Jinghong hydropower station by distributed optical fiber temperature measurement system[J].Journal of Hydroelectric Engineering,2007,26(1):97－101.

[5]秦一涛,刘剑鸣,夏旭鹏,等.分布式光纤温度监测系统在长调水电站的应用实践[J].大坝与安全,2004,(1):45－48.QIN Yi-tao,LIU Jian-ming,XIA Xu-peng,et al.Distributed optical fiber temperature monitoring system and its application[J].Dam&Safety,2004,(1):45－48.

[6]牛栋,张义,王敦厚,等.分布式光纤测温系统在西龙池水库监测渗流[J].山西水利科技,2009,(2):4－6.NIU Dong,ZHANG Yi,WANG Dun-hou,et al.Monitoring seepage flow in Xilongchi reservoir by distributed fiber optic temperature sensor system[J].Shanxi Hydrotechnics,2009,(2):4－6.

[7]肖衡林,张晋锋,何俊.基于分布式光纤传感器技术的流速测量方法研究[J].岩土力学,2009,30(11):3543－3547.XIAO Heng-ling,ZHANG Jin-feng,HE Jun.Research on measuring method of flow velocity based on distributed optical fiber sensing technology[J].Rock and Soil Mechanics,2009,30(11):3543－3547.

[8]吴志伟,宋汉周.地下水温度示踪理论与方法研究进展[J].水科学进展,2011,22(5):733－740.WU Zhi-wei,SONG Han-zhou.Temperature as a groundwater tracer:Advances in theory and methodology[J].Advances in Water Science,2011,22(5):733－740.

[9]HEALY R W,RONAN A D.Documentation of computer program VS2DH for simulation of energy transport in variably saturated porous media[R].Denver:U S Geological Survey Information Center,1996.

[10]VGENUCHTEN M T H.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J].Soil Science Society of America Journal,1980,(44):892－898.

[11]LU Sen,REN Tu-sheng,GONG Yuan-shi.An improvedmodel for predicting soil thermal conductivity from water content at room temperature[J].Soil Science Society of America Journal,2006,71(1):8－14.

[12]陈晓冬,金旭,管彦武.长春地区地表温度日变、年变对地温测量的影响[J].地球物理学进展,2006,21(3):1008－1011.CHEN Xiao-dong,JIN Xu,GUAN Yan-wu,et al.The influence of daily and annual variation of the surface temperature on near-surface temperature survey[J].Progress in Geophysics,2006,21(3):1008－1011.

[13]孔德丽,石自堂.土石坝非饱和渗流参数分析[J].中国水运,2010,10(2):91－96.KONG De-li,SHI Zi-tang.Parameters analysis of unsaturated seepage of earth dam[J].China Water Transport,2010,10(2):91－96.

[14]CARSEL R F,PARRISH R S.Developing joint probability distributions of soil-water retention characteristics[J].Water Resources Research,1988,24(5):755－769.

[15]于玉贞,林鸿州,李荣建,等.非稳定渗流条件下非饱和土边坡稳定分析[J].岩土力学,2008,29(11):2892－2898.YU Yu-zhen,LIN Hung-chou,LI Rong-jian,et al.Stability analysis of unsaturated soil slope under transient seepage flow state[J].Rock and Soil Mechanics,2008,29(11):2892－2898.

[16]谌宏伟,陈鸿汉,何江涛,等.北京市永定河冲洪积扇沙砾层非饱和水力学参数估计[J].水文地质工程地质,2008,(5):64－67.CHEN Hong-wei,CHEN Hong-han,HE Jiang-tao,et al.Estimation of unsaturated hydraulic parameters of sand and gravel of alluvial-proluvial fan of Yongding River in Beijing[J]Hydrogeology&Engineering Geology,2008,(5):64－67.

[17]朱伯芳.库水温度估算[J].水利学报,1985,(2):12－21.ZHU Bo-fang.Prediction of water temperature in reservoirs[J].Journal of Hydraulic Engineering,1985,(2):12－21.