弧焊机器人焊接马鞍型焊缝运动过程仿真

何佳斌 吴志生 李乐乐

（太原科技大学焊接技术研究所，太原，030024）

0 引言

马鞍型空间曲线是一种典型的、复杂的空间曲线，在焊接马鞍型焊缝的实际生产中，焊枪沿着焊缝的位置移动也伴随着姿态变化，其位姿变化轨迹较复杂。本文针对Motoman-UP6 型弧焊机器人实现焊接马鞍型焊缝的轨迹运动仿真，这对研究机器人自动化焊接空间曲线焊缝起指导作用[1]。

Motoman-UP6 型弧焊机器人是典型的三维开环链式机构的工业机器人，具有六个串联转动关节轴，如图1 所示，分别为S 轴、L 轴、U 轴、R 轴、B 轴和T 轴，并且在其工作空间内，可以实现工具末端点（TCP）的任意空间位置与姿态。

图1 Motoman-Up6 弧焊机器人

1 机器人三维建模及结构描述

1.1 机器人三维建模

在对机器人实体三维建模时，可以简化机器人模型中对运动仿真不影响的细节部分，只要保证机器人模型的外部轮廓以及关节位置和机器人实体一致，其运动学仿真结果与实际运动学结果就是等价的。

通过以上思想，这里对机器人模型进行合理的简化，减少模型的零件数，利用三维建模软件Solidworks 建立整个机器人各构件的实体模型，包括基座、转台、大臂、拐杆、小臂、末端和焊枪。然后，通过各构件之间转动关节的约束定义，得到UP6 型弧焊机器人装配体模型如图2 所示，弧焊机器人结构尺寸如图3 所示。

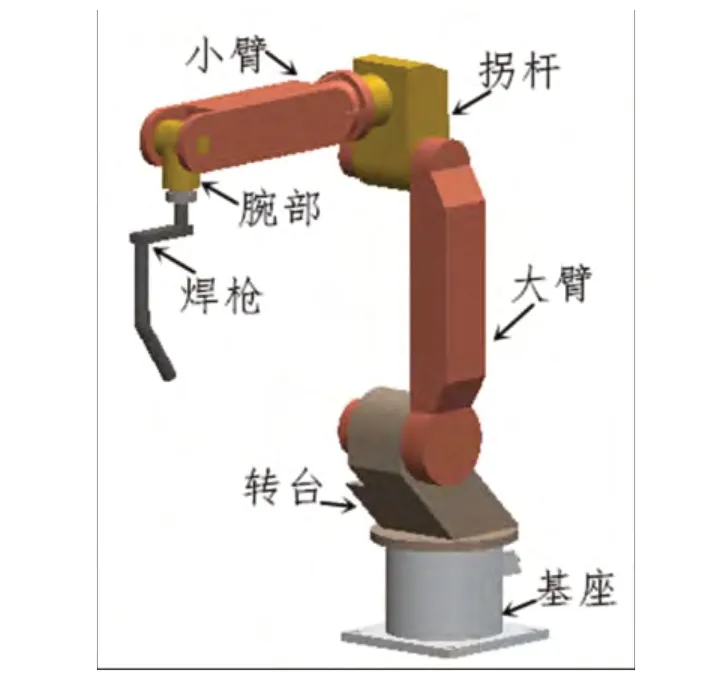
图2 UP6 弧焊机器人装配体模型

图3 UP6 弧焊机器人结构尺寸

1.2 机器人结构描述

在机器人运动学中，机械臂可以看成是由一系列连杆通过关节连接而成的一个运动链，需要通过定义某些参数来具体描述这个运动链。采用修正后的Denait-Hartenberg（D-H）理论[2]，本文将轴S、轴L、轴U、轴R、轴B和T 轴（如图1 中所示）分别标记为轴1-轴6，并且将基座、转台、大臂、拐杆、小臂、腕部和焊枪（如图2 中所示）分别标记为连杆0-连杆6。

用连杆长度 ai−1（关节轴i -1和关节轴i 之间公垂线的长度，由关节轴i -1指向关节轴i）和连杆转角 （按右手定则绕 ai−1从关节轴i -1到关节轴i 的角度）作为描述连杆i -1的参数，

节轴i 同向）关节角度θi（按右手定则绕关节轴i 从α i−1

用连杆偏距 di（αi−1和 αi之间公垂线的距离，与关

到 αi的角度）作为描述关节轴i 的参数，其中对于运动

链的末端连杆， ai−1和αi−1习惯设置为0，即 a0=a6= 0，α0=α6= 0。在这里提出了D-H 参数的方向性，其主要是为了后面建立连杆坐标系提供方便，并能够直接引入

表1 Motoman-UP6 机器人的D-H 参数表

1.3 机器人连杆坐标系建立

机械臂相邻连杆之间的空间关系是通过固接的连杆坐标系之间的空间关系来描述，首先需要在每个连杆上定义一个固接的连杆坐标系，其建立规则如下[2]：

1）坐标系{i}的iZ 轴沿关节轴i 由公垂线 1ia−指向公垂线ia （当id =0 时，iZ 垂直于 1ia−和ia 所在的平面）;

2）坐标系{i}的 iX 轴沿公垂线ia 由关节轴i 指向关节轴 1i+ （当 ia =0 时，iX 垂直于iZ 和 1iZ+所在的平面）;

3）坐标系{i}的原点位于公垂线 ia 与关节轴i 的交点处，坐标系{i}的iY 轴可由其他两个按右手定则得到。

图4 所示为UP6 机器人各连杆坐标系，连杆坐标系{0}-连杆坐标系{6}依次固接在机器人基座、转台、大臂、拐杆、小臂、腕部上，图中X0方向与Z0方向构成了坐标系{0}，其中Y0方向按右手定则得到，后面连杆坐标系同理。固连在基座上的连杆坐标系为{0}，它是一个固定不动的坐标系，为了简便，通常设定当1θ =0°时，坐标系{0}与坐标系{1}重合，同理，固连在机器人腕部的连杆坐标系为{6}，取 =0°时，连杆坐标系{5}的X5轴与连杆坐标系{6}的X6轴重合。

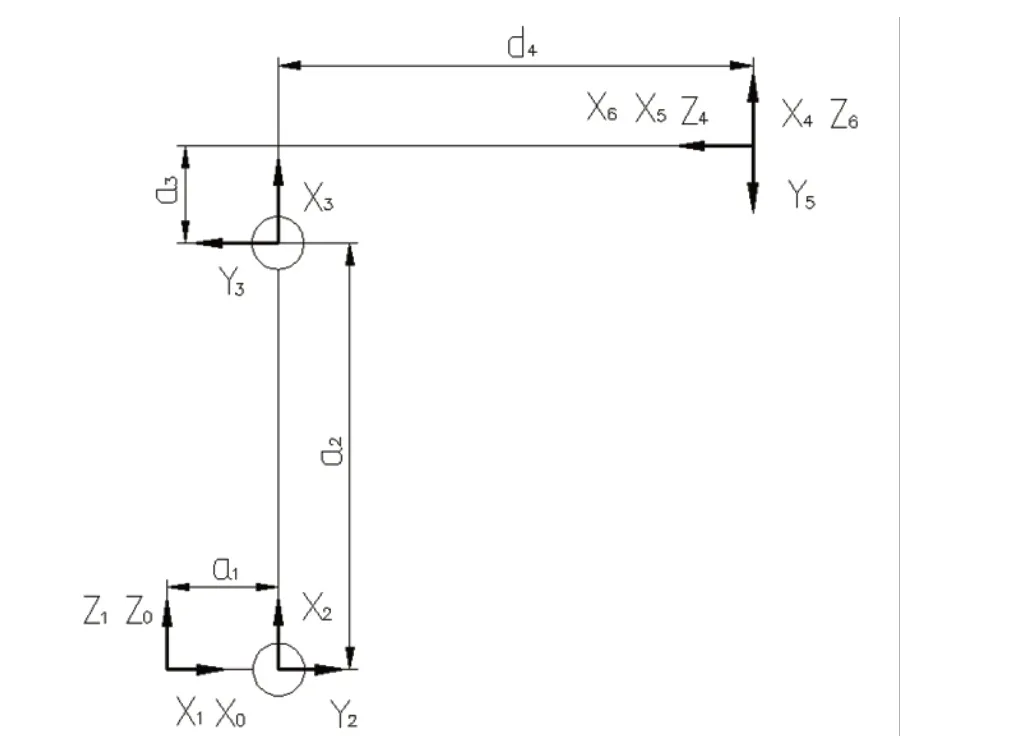
图4 UP6 机器人连杆坐标系

2 机器人运动学

利用以上的四个D-H 参数，关节角度iθ 、连杆偏距连杆转角 ai−1和连杆长度 构建出连杆坐标系{i}相对于连杆坐标系{i-1}的变换矩阵[2]：

式（1）中 icθ 表示的是cosiθ ，isθ 表示的是siniθ下式同；

故由上面的机器人D-H 参数可以得到各个相邻连杆坐标系之间的变换矩阵，如下式（2）-式（7）所示。

所以，可以得到连杆坐标系{6}相对于连杆坐标系{0}的变换矩阵为：

06T 是

关于6 个关节轴角的函数，可以根据各关节角度θi计算出固接在腕部的连杆坐标系{6}相对于固接在基座的连杆坐标系{0}的位置和姿态。

3 焊缝坐标系建立

本文中焊接工件为两个垂直相交的的圆管，其半径分别为100mm（r）和200mm（R），如图5 所示。焊缝坐标系（表示为坐标系{Hi}，0 ≤i ≤n，n 为空间曲线离散点个数）是用来描述空间曲线焊缝的。坐标系{Hi}的坐标原点和基轴轴向分别表示的是焊枪末端沿着焊缝运动在i 时刻的位置及姿态，X 轴表示焊缝曲线的切线方向，也即焊枪的前进方向，Z 轴表示焊缝曲线的法线方向，也即焊枪的轴向。图中坐标系{G}表示的是工件中心坐标系。

图5 焊缝坐标系

在工件中心坐标系{G}中，建立空间曲线方程为：

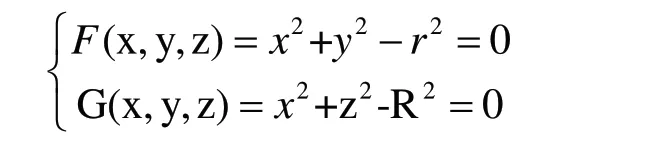
利用Matlab 将该焊缝轨迹的数学模型提取出来，并将其轨迹曲线均匀离散化处理后，计算出每个离散点的位置及姿态，即构成焊缝坐标系。

焊缝坐标系{Hi}相对于工件中心坐标系{G}位姿矩阵可表示为[3]：

3.1 位置计算

各离散点的位置计算，也即焊缝坐标系{Hi}原点位置计算。

在Matlab 中绘制该马鞍型焊缝轨迹线，得到如图6所示马鞍型焊缝方向矢量中的黑色曲线。

3.2 姿态计算

各离散点的姿态计算，也即焊缝坐标系{Hi}基轴轴向计算。

方向向量 ∶焊枪前进方向，为空间焊缝曲线的切线方向，即图6 中蓝色箭头线所示；

方向向量 ∶焊枪轴线方向，为焊缝曲线法平面与两个圆管曲面所成曲线的切线夹角的平分线方向，如图6 所示，黄颜色箭头线为曲线法平面与圆管R 所成曲线的切线方向，粉红色箭头线为曲线法平面与圆管r 所成曲线的切线方向。

在Matlab 中执行以上运算过程的编程，得到其焊缝坐标系{Hi}（0 ≤i ≤100）如图7 马鞍型焊缝坐标系。

图6 马鞍型焊缝方向矢量

图7 马鞍 型 焊 缝 坐 标系

4 机器人转换方程建立及Matlab 逆解计算

4.1 机器人转换方程建立

机器人逆运动学是在已知工具坐标系相对于基坐标系的期望位置与姿态，计算一系列满足期望要求的关节角度。只要通过运动学方程推导出腕部连杆坐标系{6}相对于基座连杆坐标系{0}的变换矩阵06T，即可利用Matlab中的Robotic toolbox 求解出机器人各关节角。

由于在当工具末端处于目标位姿时，工具末端坐标系{7}与焊缝坐标系{Hi}将重合，如图8 所示为弧焊机器人系统坐标系转换，图中坐标系{S}为工作台坐标系，其相对于基座坐标系{0}固定不动。从而构建机器人运动学方程如式（10）所示，等式左边为工具末端的连杆坐标系{7}相对于基座坐标系{0}的变换矩阵，等式右边为焊缝坐标系{Hi}相对于基座坐标系{0}的变换矩阵。

图8 弧焊机器人系统坐标系转换

所以得到：

式中 T06表示机器人腕部坐标系{6}相对于基座坐标系{0}的转换矩阵；

T67表示工具末端坐标系{7}相对于机器人腕部坐标系{6}的转换矩阵；

TS0表示工作台坐标系{S}相对于基座坐标系{0}的转换矩阵；

TGS表示工件坐标系{G}相对于工作台坐标系{S}的转换矩阵；

THGi

表示焊缝坐标系{Hi}相对于工件坐标系{G}的转换矩阵。

经过转换，得到：

由于工作台坐标系{S}相对于基座坐标系{0}的位姿是固定不变的，所以0ST为已知矩阵，同理SGT 和67T也是已知的。本文在计算中有：

4.2 Matlab 逆解计算

利用Matlab 中的Robotics Toolbox 建立UP6 机器人数学模型，并求其对应位姿逆解[4]，在逆解之前可以通过验证：

时，得到其轴坐标分别为[0 –pi/2 0 0 pi/2 0]和[0.35 -1.22 0.52 0.70 -3.84 1.05]，并得到机器人各轴位姿图形[5]如图9、图10 所示，可以看到其逆解可靠。

建立机器人模型及其求逆程序如下：

L1=link([0 0 0 0],'modified');

L2=link([-pi/2 150 -pi/2 0],'modified');

L3=link([pi 570 0 0],'modified');

L4=link([-pi/2 130 0 -640],'modified');

L5=link([pi/2 0 pi/2 0],'modified');

L6=link([pi/2 0 0 0],'modified');

r=robot({L1 L2 L3 L4 L5 L6});

r.name='Motoman-UP6';

T=0sT*sgT*ghT*(67T)^-1;

q=ikine(r,T,[0 pi/2 0 0 -pi/2 0]);

图9 Matlab 机器人逆解1

图10 Matlab 机器人逆解2

5 机器人焊接计算机仿真

利用Solidworks 中的Motion 插件进行机器人运动仿真实验， 将Matlab 中所得各关节坐标输入到Solidworks 建立的机器人模型6 个关节中，关节坐标通过样条曲线插值拟合，使关节运动平稳。如图11 所示为5s 内机器人关节轴角随时间变化散点图，图中每个星点、散点表示的是该时刻对应的各关节轴角值。关节角1-5 的散点在整个仿真时间内均呈现周期性的弦曲线分布，且周期均为5s，在结束时刻各轴回到初始角度，整体来看轴角散点在曲线的极点时刻都分布较密集，而在曲线极点的过渡时刻分布较稀疏。关节角6 的散点从0°-360°以2.5s 为周期呈现规律性波动上升，散点分布均匀。

图11 机器人轴坐标随时间变化曲线

如图12 所示为弧焊机器人焊接马鞍型焊缝仿真过程帧图，在整个仿真过程中焊枪末端点（焊丝端点）始终与焊缝轨迹点保持协调吻合，焊枪的轴线方向（焊枪坐标系{7}的Z 轴方向）始终沿焊缝轨迹点的Z 轴方向，焊枪的前进方向（焊枪坐标系{7}的X 轴方向）也始终沿焊缝轨迹点的X 轴方向。

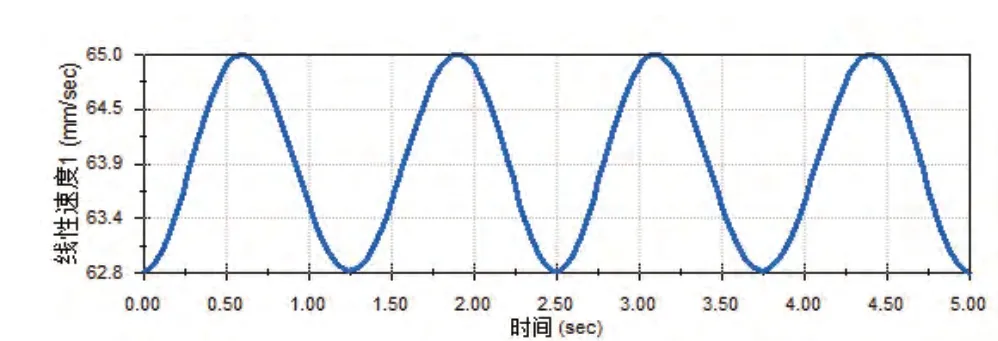
图14 焊枪末端仿真过程线性速度变化曲线

图15 焊枪末端仿真过程线性加速度变化曲线

图12 弧焊机器人焊接马鞍型焊缝仿真帧图

如图13-图15 所示焊枪末端仿真过程中的位移、速度及加速度随时间变化曲线，其变化也均呈周期性。

图13 焊枪末端仿真过程线性位移变化曲线

6 结论

1）为了实现模型关节角度方向与实体关节角度方向相一致，连杆坐标系Z 轴方向须按照右手定则确定，这对于运动仿真的真实性非常重要。引用修改后的D-H 参数法，并提出了D-H 参数的方向性，这对于后面建立连杆坐标系十分方便，在建立运动学方程时可以直接引用John. J. Craig 提出的连杆变换矩阵 。

2）机器人Motion 运动仿真轨迹跟数学模型一致，证明所建的运动学方程与焊缝坐标系正确，并通过数据点间的样条曲线插值拟合，完成了数据点间的平稳过渡，所得轨迹圆滑无棱角，联合Matlab 的Robotic toolbox 逆解计算以及Solidworks 的三维仿真，完成了机器人从运动控制到模型运动的整个过程，这对后期实现离线编程与仿真有重要作用。

[1] 陈光伟.导管架焊接接头空间轨迹规划研究[D].天津：天津工业大学,2010.

[2] Craig J J.机械人学导论[M].北京∶机械工业出版社,2006.

[3] 刘永,王克鸿,杜姗姗,等.弧焊机器人空间焊缝焊接参数与姿态规划研究[J].南京理工大学学报,2003,27(2)∶144-147.

[4] 任福深,陈树君,殷树言,等.管道插接焊缝位置及焊枪位姿建模[J].焊接学报,2008,29(11)∶33-36.

[5] 左富勇,胡小平,谢珂,等.基于Matlab Robotics 工具箱的SCARA 机器人轨迹规划与仿真[J].湖南科技大学学报,2012,27(2)∶41-44.

[6] Corke P I.A Robotics Toolbox for Matlab[J].IEEE Transactions on Robotics and Automation,1996(1)∶24-32.?