基于股价跳跃限制的高管股票期权激励定价研究

刘 井 建， 焦 怀 东， 付 杰

（1.大连理工大学 经济学院，辽宁 大连116024；2.大连理工大学 证券期货研究中心，辽宁 大连116024）

近年来，股票期权逐渐成为我国上市公司普遍采用的高管激励手段之一［1］。当公司业绩表现较好时，股票期权的内涵价值随着股价上升而增大，提高了高管的预期报酬水平；当公司业绩不佳时，股价下跌，股权内涵价值降低甚至为零，从而使高管这一未定薪酬和公司业绩（价值）存在高度的敏感性，达到实现激励高管提高公司业绩（价值）的目的［2］。股权激励价值的评估是高管薪酬合约设计的基础。研究者一直不断探索新的股权价值定价模型与方法，使之能够最大程度地反映股权激励的真实内在价值。最为常用的模型当数Black－Scholes（BS）资产定价模型，它认为资产（如股票）价格运动遵循一种扩散过程，后来研究者证实并引入了跳跃过程。

国内外学者对股票期权的定价方兴未艾，最早可追溯到Bachelier的投机交易理论，他开创性地使用随机游走的思想描述股票价格的运行轨迹，得出到期日期权价值的期望公式［3］。由于随机游走可能得出股价为负的情形，在现实中股价却不会出现负值，进而试图采用对数正态分布描述股价分布，尽管规避了股价为负的情形，但这仍然存在许多争议。在随机游走的扩散模型的基础上，为了描述股价的剧烈波动现象，后来引入了跳跃的思想。早在1976年Merton提出了正态跳跃扩散模型，采用几何布朗运动描述系统风险引起的股价波动，引入Poisson过程刻画非系统风险引起的价格跳跃，并基于跳跃幅度服从正态分布的假设，得出了欧式期权定价的公式［4］；Amin提出了弱收敛于带跳跃的连续股价过程的离散化模型，将离散的跳跃扩散过程代替几何布朗运动描述股价的变动，并运用倒推方法推导出期权定价公式［5］；胡素华、张世英和张彤将跳跃因子引入抛物线扩散模型，得出了资产价格的抛物线跳跃扩散模型［6］。

立足于扩散和跳跃的理论假设，研究者进行了许多拓展研究。马超群等假定股票价格行为服从混合过程，并基于BS模型得出了看涨期权定价公式［7］；张静等在假定资产价格服从跳跃扩散过程的基础上，给出了具有固定敲定价格的算术平均亚式期权价格的下界表达式［8］；马宇超等构建了带均值回归项的跳跃扩散模型，并运用上证指数进行参数估计和数值分析，结果表明该模型更好地模拟了中国股市的变动［9］。后来引入了定义在概率空间上的随机Lévy过程描述股价运动。例如，Geman等推导得出了基于Lévy过程描述股价波动的期权定价公式［10］；Nowak和Romaniuk提出了基于Lévy过程的带模糊参数的欧式期权定价模型［11］。

由于金融市场波动性和信息不完全，期权定价模型中的一些参数难以准确描述，许多研究引入了模糊集理论。例如，Chrysafis等通过模糊估计BS模型中的波动率提出了基于模糊环境的期权定价模型，但和资产价格的实际波动偏差较大［12］；Xu和Wu采用了模糊集理论和随机理论描述金融市场的不确定性，提出了欧式期权定价的模糊正态跳跃扩散模型［13］。此外，关于模糊环境下欧式期权定价的双指数跳跃扩散模型［14］、数值模型等也得到了进一步的研究［15］。

在通常的研究假设中，标的股票价格服从几何布朗运动且范围是无界的，然而，即使在欧美证券交易市场中，股票的价格并不总是无约束的自由运动，尤其是我国股票市场存在涨跌停板制度，这一制度限制导致股票交易价格的波动是有界的，不再满足传统股权定价模型关于股价运动无界的假设，因此有必要引入股票涨跌停的边界和概率分布。本文即在基于股价遵循随机布朗运动的扩散过程基础上，考虑到我国资本市场的涨跌停限制的制度设计，并将之引入股价的跳跃过程，提出了股价跳跃限制的股票期权价值定价模型，以我国实施股权激励的公司为样本，对定价模型进行模拟并和传统的BS定价模型的评估结果进行比较分析，以验证定价模型的适用性。

一、股权激励特征与BS定价模型

1.股权激励的特征

授予高管的股票期权和一般的可交易的期权存在许多异同点。相同之处如股权执行价格一般依据标的股票在一定时期的价格水平确定，无风险利率则参照相同期限的银行利率或国债到期收益率；不同之处在于高管激励股权的流动性较差，行权条件较为严格，最为显著的是预期寿命和波动率难以确定。

授予高管激励股权的解冻期与行权期并不相同，解冻期一般要早于行权日，因此高管激励股权在寿命期内具有美式期权的特征。此外，高管激励股权普遍还具有等待期权的特征，因此为了计算出较为可靠的寿命期，一般利用行权日期和取消概率进行估算。若公司曾实施股权激励计划，可以借鉴历史等待期和行权份额对股权寿命的影响进行评估；否则参考类似公司的行为推算寿命期。一般来说，高管激励股权的期望寿命大于等待期，并且基于理性人的假设，在现实实践中波动率越高，行权的时间可能越早［16］。

标的股票的预期波动率决定了未来损益的分布，波动率的轻微变化都会对股权价值产生明显的影响。在无股利分红的条件下，预期波动率通常根据股票历史价格进行估计，采用股票价格的标准差计量。对于复杂的情形，一般根据类比法进行假设和估算。类比法是通过对现实情形和历史数据进行比较估计，但估计值和实际值仍可能出现较大的偏差，尤其对于新上市的公司股票，估计波动率难度更大。当然，传统的参数复制带来的误差与模型选择、真实测度的漂移项以及真实状态变量等存在紧密的关系［17］。

不难发现，高管激励股权价值定价的关键是确定未知参数，寿命期相对容易测度，但最难描述的核心变量是波动率，而如何科学地描述股价的运动特征，是估计波动率的基础。我们将在传统的扩散－跳跃的资产定价模型的基础上，考虑我国存在涨跌停板限制的约束制度，将这一特征嵌入并构建高管激励股权价值的定价模型。

2.股权Black－Scholes定价模型

假定股票价格S服从几何布朗运动，则有：

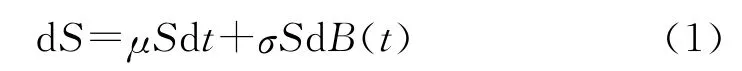
其中，漂移项或股票收益率μ和波动率σ为常数，B（t）为标准的布朗运动。

假设V表示金融衍生产品如期权的价值，它是关于标的股票的价格和时间的函数，根据伊藤引理，则有：

在无套利空间的前提下，可以构造一个投资组合，使其期望报酬率与无风险资产的报酬率相等，从而得出著名的BSM偏微分方程式：

偏微分方程（3）根据不同的边界条件，可以计算出以S为标的资产、不同形式的金融衍生产品的价值。如果假设边界条件符合欧式看涨期权的边界条件，即：在到期日时，收益函数为V（S（T））＝max｛S（T）－K，0｝，则其金融衍生产品的价值表示为：

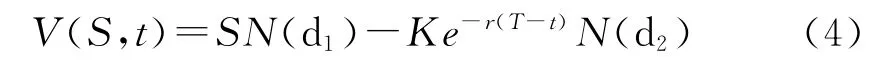
二、股价跳跃限制定价模型

传统的期权定价方法是基于标的资产价格运动，是连续的扩散过程，然而现实情形中却存在跳跃现象，这一特征在连续的扩散过程中却未体现。我国证券市场和欧美市场在交易制度上的差异之一是涨跌停板制度，如A股股票的涨跌停板限制是10%，ST类股票的涨跌停板限制是5%，而这一制度约束为跳跃限制提供了实践依据，因此需要对跳跃临界幅度或阈值限制进行定义。将股价发生涨停或跌停时视为跳跃，且股价跳跃是有限制的。本文定价模型可以在股价遵循几何布朗运动的基础上，加入随机的限制性跳跃，开展对股权定价模型的研究。

1.基本假设

假设在无摩擦、无套利的金融市场中，仅存在两种可连续交易的证券：第一为无风险债券，记作B，价格满足dBt＝rBtdt；第二为股票，价格过程S（t）满足随机微分方程：

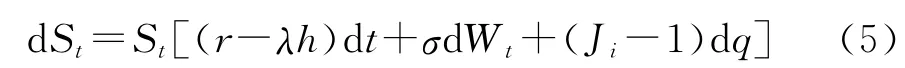
其中，r为无风险利率，σ为股价未发生跳跃时的波动率，均为常数。dq是一个Poisson过程，即在很小的时间间隔dt中，q发生一次跳跃的概率为λdt，不发生跳跃的概率为1－λdt，λ是单位时间内发生跳跃的次数；｛Ji｝i≥1是在正实数区间上平方可积且独立同分布的随机变量，表示股票价格发生跳跃的幅度。假定均定义在风险中性概率空间（Ω，F，Ft，P）且相互独立，则Ft是由Wt、｛Ji｝i≥1及dq联合生成的σ－代数流。

跳跃过程的（Ji－1）Stdq可以解释为：在Poisson过程的某一随机时刻，发生了一次（Ji－1）的跳跃，资产价格由原来的St变为（Ji－1）St，随机变量J服从对数正态分布，即lnJ～N（μj，），h＝E（J－1）＝选择合适的等价鞅测度，可以使期权的均衡价格等于未来收益折现值的数学期望，而价格过程S（t）也可在该测度空间下定义，且相应的性质并未发生改变。

进一步的，lnJ是指St在t时刻发生跳跃的幅度，由于股价扩散过程与跳跃过程是相互独立的，因此扩散过程中lnJ的取值是无差异的，lnJ的分布可进一步简化为三点分布，即当标的股票涨停时取值为0.1，跌停时取为－0.1，令前两种情况出现的概率分别为p和q，其他情形出现的概率为1－p－q，取值均为0，相关取值可以通过股票高频交易的历史数据分析获得。

2.定价模型

根据Ito－Skorohod随机微分方程解的结构可知，式（5）的解为：

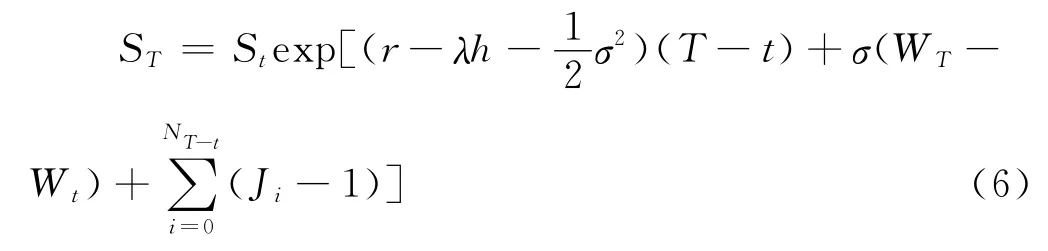
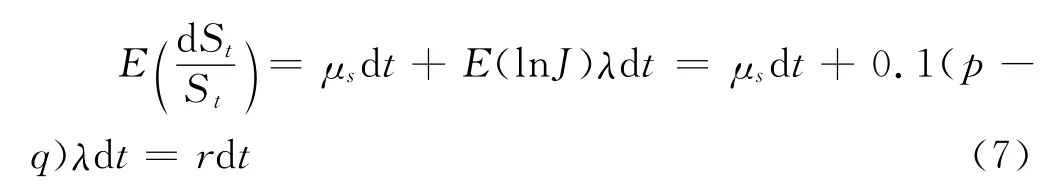
当μs＝r－0.1（p－q）λ时，股票价格满足风险中性的条件，式（6）可改写为：

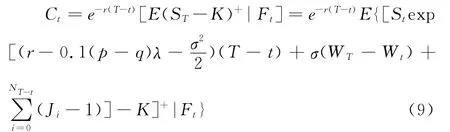
假设在未来时期（t，T］期间，共发生了n次跳跃，表示为q（t，T］＝n，根据独立性条件可知，将这一条件限制加入式（9）后，并不影响结果的变化，进一步转换为：

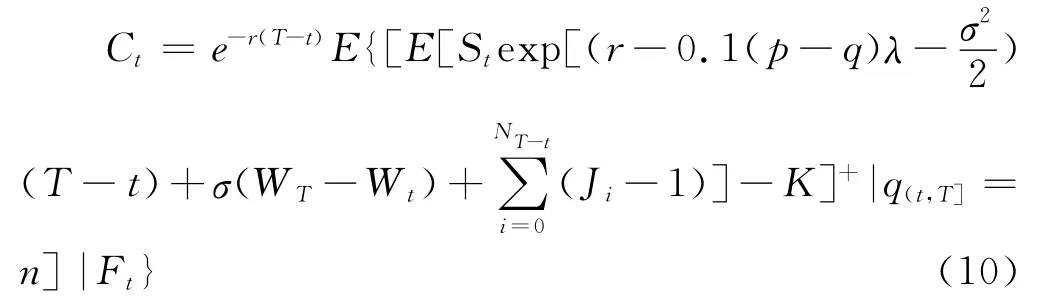
因为发生跳跃的次数服从Poisson分布且与股价的扩散过程相互独立，则有：

理论上讲，随着时间窗口选择长度的增加，可观测到的跳跃点越多，根据Lindberg－Lévy中心极限定理，独立同分布、且数学期望和方差有限的随机变量序列之和是以标准正态分布为极限，由先前的假设可得：

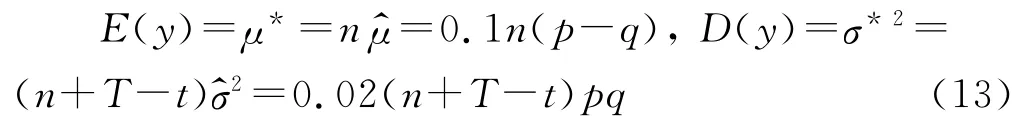
因此有：

综上可得期权在t时刻的价值Ct可以表示为：

三、模型仿真与结果分析

1.数据来源

通过高管激励股权价值的扩散－涨跌停跳跃限制的定价模型，得出了股权价值与标的股票价格之间的函数关系。利用锐思（Resst）数据库关于股票交易价格的高频数据，选取2008～2012年公布并实施股票期权激励计划的公司，共有沪深两市235家上市公司。进一步地，利用Matlab 2010软件，将2008年1月1日至2009年6月30号的股票交易价格数据作为训练样本，然后应用训练的轨迹对2009年7月1日至2010年12月31号的股票运动价格和期权价值进行模拟，交易数据采用日交易数据。

2.模拟结果分析

以中兴通讯（000063）为例，2008年1月1日至2009年6月30日期间中兴通讯股票共有364个交易日，出现涨停板3次（分别是2008年9月19日、2008年11月17日和2008年11月19日），跌停板4次（分别是2008年1月2日、2008年10月8日、2008年10月9日和2008年10月27日），因此对应公式中的参数p＝4／364，q＝3／364，n＝7，λ＝7／6。这里按照季度计算，6个季度共发生7次停板。

2008年一年期定期存款利率为2.25%，为应对金融危机带来的冲击，我国推行了4万亿的经济刺激政策，与此同时CPI不断上升，利率也表现出上浮的趋势。按照一般的处理方法，通常采用一年期定期存款利率为无风险利率，为方便计算，假定无风险利率为3%。2008年1月至2009年6月中兴通讯股票价格的波动率为11.3%。由于模拟的是数据离散化的过程，因此从标准正态分布中抽取随机数作为波动率放大或缩小的倍数，再从三点分布中抽取是否发生跳跃过程的参数，代入式（14），就能获得股价与期权价值的运动路径。模拟股价与期权价值走势见图1，其中波动较大的是期权价格曲线，波动较小的是股票价格曲线。期权价值曲线波动大的原因是由于期权价格曲线的坐标的步长较小。表1是其中的一条路径，最后所得的价格为21.44，这个数值可以认为是6个时间间隔（季度）股票价格运行的一种可能的轨迹。当然，随着随机取样的差异，轨迹也会发生变化。为了降低随机取样差异引起的大幅波动，本文模拟了50次然后取平均值作为最终结果，基本考虑了价格变化的各种分布状况。在加入我国特殊的股票价格涨跌停板制度后，相较于传统的BS定价模型计算的结果，模拟结果都比BS模型计算的结果要小，根据Merville等学者的研究结论［18］，BS定价模型对离散度较高的看涨期权普遍存在高估的可能，并且Armstrong和Vashishtha等研究者也证实了这一结论［2］。

图1 中兴通讯模拟价格走势

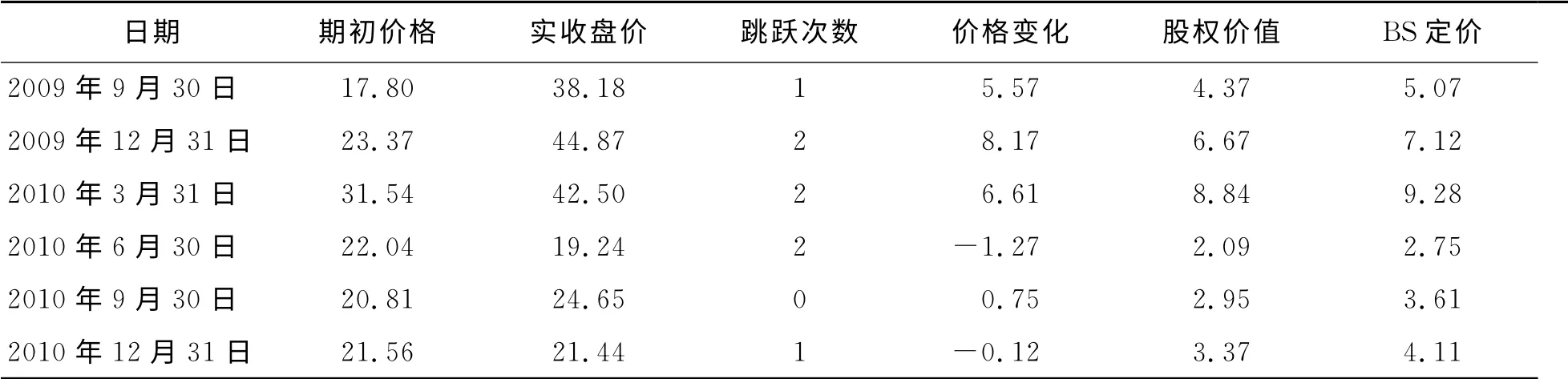
表1 r＝0.3，σ＝0.35，ΔT＝0.25时股价模拟

后期我们随机选取了其他实施股权激励公司的股票进行模拟，都得出了类似的结果，即模拟结果相较于BS模型要小。对于任何期权价值的准确估计，目前大都是以BS定价模型为基准，尽管存在一定的局限性，但是当前仍然缺乏更为可靠的替代模型，即当高管激励股权在市场进行交割时，股权价值仍是依据传统的定价模型。因此，本文提出的股票期权定价模型也是以BS定价模型为基准，引入我国特殊的涨跌停板制度，试图对股权激励价值进行更为科学合理的定价。

四、研究结论与建议

本文将我国证券市场的涨跌停制度引入到期权定价模型中，得出了如式（14）表示的期权定价公式，通过数值模拟的方法对模型计算出的期权价值与BS模型理论值进行比较，所得出的期权价值显著低于BS模型值，对于高管激励股权的价值评估具有一定的借鉴作用。就方法而言，在传统的扩散－跳跃的股权定价模型的基础上，引入我国的涨跌停板限制，创新性地运用三点概率分布刻画这一特征，从而将我国证券市场的制度特征模型化；不足的是，在实际操作中，由于选择训练的样本窗口与模拟窗口的期间差异，股票市场不断受到外部环境变动引发的冲击，与传统的模拟方法类似，利用样本数据训练出的趋势进行预测不可避免存在一定的偏差，但结论较为符合当前关于BS模型存在价值高估的观点。

实施公司高管股票期权已成为当下较为流行的激励方式，如何评估其真实价值的相关研究仍然较少，即使是广泛采用的公允价值定价法，也亟需科学的测算模型［19］，由此本文结合我国证券市场涨跌停板制度对期权价值进行研究。然而，我国期权市场还处于起步阶段，中金所正在运行的期权模拟交易盘中依然运用的是传统BS模型的理论值，因此以BS期权定价模型为基础的定价方法对实践操作具有重要的作用，但是许多投资者对期权类衍生品还较为陌生，对于以期权为标的的结构化产品了解更为有限，在操作过程中缺乏足够的理性，这往往导致市场价格偏离于理论价格。因此，构建适用于我国证券市场特征的定价模型并进行推广应用，对我国公司实施高管股权激励合约设计以及期权市场交易等具有重要的借鉴意义。

［1］MERCHANT K A，VAN DER STEDE W A，YU Z.Performance measurement and incentive compensation：an empirical analysis and comparison of Chinese and western firms’practices［J］.European Accounting Review，2011，20（4）：639－667.

［2］AMSTRONG C S，VASHISHTHA R.Executive stock options，differential risk－taking incentives，and firm value［J］.Journal of Financial Economics，2012，（104）：70－88.

［3］BACHELIER L.Louis Bachelier’s Theory of Speculation：The Origins of Modern Finance［M］.Princeton：Princeton University Press，2011.34.

［4］MERTON R C.Option pricing when underlying stock returns are discontinuous［J］.Journal of Financial Economics，1976，3（1－2）：125－144.

［5］AMIN K I.Jump diffusion option valuation in discrete time［J］.Journal of Finance，1993，48（5）：1833－1863.

［6］胡素华，张世英，张彤.资产价格的抛物线跳跃扩散模型［J］.系统工程理论与实践，2006，（3）：1－10.

［7］马超群，陈牡妙.标的资产服从混合过程的期权定价模型［J］.系统工程理论与实践，1999，（4）：42－47.

［8］张静，何春雄，郭艾.跳跃－扩散模型下亚式期权的定价［J］.系统工程，2010，（12）：96－99.

［9］马宇超，陈敏，蔡宗武.中国股市权证定价的带均值回归跳跃扩散模型［J］.系统工程理论与实践，2010，（1）：14－21.

［10］GEMAN H.Pure jump lévy processes for asset price modeling［J］.Journal of Banking ＆Finance，2002，26（7）：1297－1316.

［11］NOWAK P，ROMANIUK M.Computing option price for lévy process with fuzzy parameters［J］.European Journal of Operational Research，2010，201（1）：206－210.

［12］CHRYSAFIS K A，PAPADOPOULOS B K.On theoretical pricing of options with fuzzy estimators［J］.Journal of Computational and Applied Mathematics，2009，223（2）：552－566.

［13］XU W，WU C，XU W.A jump－diffusion model for option pricing under fuzzy environments［J］.Insurance：Mathematics and Economics，2009，44（3）：337－344.

［14］ZHANG L，ZHANG W，XU W.The double exponential jump diffusion model for pricing European options under fuzzy environments［J］.Economic Modelling，2012，29（3）：780－786.

［15］THAVANESWARN A，APPADOO S S，FRANK J.Binary option pricing using fuzzy numbers［J］.Applied Mathematics Letters，2013，26（1）：65－72.

［16］BETTIS J C，BIZJAK J M，LEMMON M L.Exercise behavior，valuation，and the incentive effects of employee stock options［J］.Journal of Financial Economics，2005，76（2）：445－470.

［17］郑振龙，刘杨树.衍生品定价：模型风险及其影响［J］.金融研究，2010，（2）：112－131.

［18］MERVILLE L J，PIEPTEA D R.Stock－price volatility，mean－reverting diffusion，and noise［J］.Journal of Financial Economics，1989，24（1）：193－214.

［19］杨春梅，梁朝晖.基于多重期权法的中国可转债价值研究［J］.大连理工大学学报（社会科学版），2014，35（3）：50－55.