A Split Least-squares Characteristic Procedure for Convection-dominated Parabolic Integro-diferential Equations
2015-02-13GUoHUIANDFUHoNGFEI
GUo HUI AND FU HoNG-FEI
(College of Science,China University of Petroleum,Qingdao,Shandong,266580)
Communicated by Ma Fu-ming
A Split Least-squares Characteristic Procedure for Convection-dominated Parabolic Integro-diferential Equations
GUo HUI AND FU HoNG-FEI
(College of Science,China University of Petroleum,Qingdao,Shandong,266580)
Communicated by Ma Fu-ming
In this paper,we combine a split least-squares procedure with the method of characteristics to treat convection-dominated parabolic integro-diferential equations.By selecting the least-squares functional properly,the procedure can be split into two independent sub-procedures,one of which is for the primitive unknown and the other is for the fux.Choosing projections carefully,we get optimal orderH1(Ω) andL2(Ω)norm error estimates foruand sub-optimal(L2(Ω))dnorm error estimate forσ.Numerical results are presented to substantiate the validity of the theoretical results.
split least-square,characteristic,convection-dominated,convergence analysis
1 Introduction
We consider the following convection-dominated parabolic integro-diferential equations:
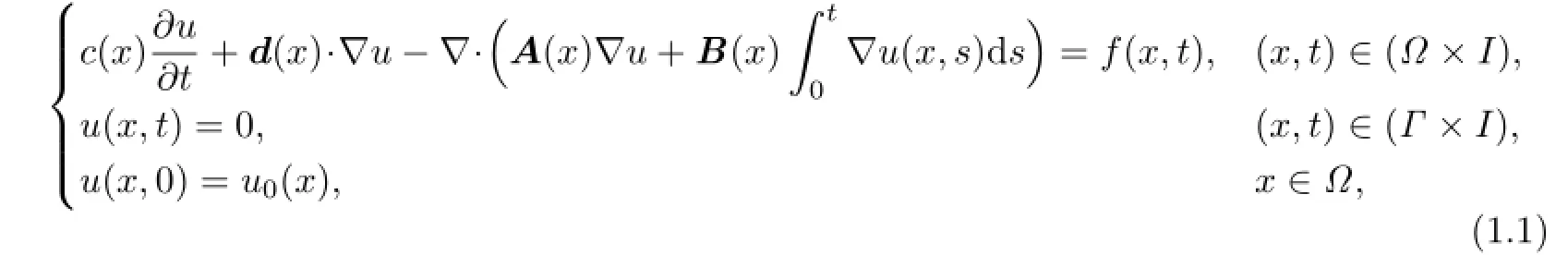
whereI=(0,T]is the time interval,Ωis a bounded polygonal domain inRd,d=2,3,with a Lipschitz continuous boundaryΓ,dis the space dimension.d(x)=(d1(x),···,dd(x))T.A(x)=(aij(x))d×d,B(x)=(bij(x))d×dare bounded,symmetric and positive defnite matrices,i.e.,there exist positive constantsa∗,a∗,b∗andb∗such that
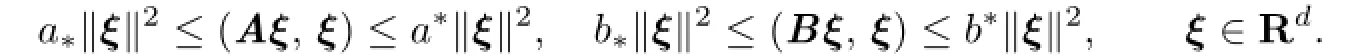
We make the following assumptions:there exist positive constantsk1,k2such that

We also assume thatΩisH2-regular:forf∈L2(Ω)the solution of the following problem
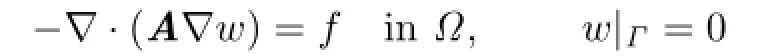
exists and‖w‖2≤K‖f‖.
This model arises from many physical processes in which it is necessary to take into account the efects of memory due to the defciency of the usual difusion equations(see [1-2]).As we all know,the numerical simulation of convection-dominated problems requires special treatment.Generally,they either smear sharp physical fronts with excessive numerical difusion,or introduce nonphysical oscillations into numerical solutions.The method of characteristic has proved efective in treating convection-dominated problems(see[3-4]).
We have introduced the least-squares method for such equations whenA,Bare proportional to a unit matrix in[5].The least-squares fnite element procedure has two typical advantages as follows:it is not subject to Ladyzhenskaya[6],Babuˇska[7],Brezzi[8]consistency condition,so the choice of approximation spaces becomes fexible,and it results in a symmetric positive defnite system.However,it usually needs to solve a coupled system of equations for conventional least-squares fnite element procedure,which brings to difculties in some extent.We only get the optimal orderH1(Ω)norm error estimate foruin[5].
In[9-10],a kind of split least-squares Galerkin procedure was constructed for stationary difusion reaction problems and parabolic problems.The purpose of this paper is to combine the split least-squares procedure with the method of characteristics for convectiondominated parabolic integro-diferential equations.The most advantage of the scheme is: by selecting the least-squares functional properly,the resulting procedure can be split into two independent symmetric positive defnite sub-schemes.One of sub-procedures is for the primitive unknown variableu,which is the same as a stand Galerkin characteristic fnite element procedure and the other is for the introduced fux variableσ.By carefully choosing projections,we see that the method leads to the optimal orderH1(Ω)andL2(Ω)norm error estimates foruand sub-optimal(L2(Ω))dnorm error estimate forσ.
The paper is organized as follows.In Section 2,we formulate the procedure.The convergence theory on the algorithm is established in Section 3.In Section 4 we give the numerical experiment.
As in[11],we assume that the problem(1.1)is periodic withΩ.In this paper we useWk,p(k≥0,1≤p≤∞)to denote Sobolev spaces(see[12])defned onΩwith a usual norm‖·‖Wk,p(Ω),andHk(Ω),L2(Ω)with norms‖·‖k=‖·‖Hk(Ω),‖·‖=‖·‖L2(Ω),respectively. For simplicity we also useLs(Hk)to denoteLs(0,T;Hk(Ω)).The inner product(·,·)is both used for scalar-valued functions and vector-valued functions.Throughout this paper, the symbolsKandδare used to denote a generic constant and a generic small positive constant,respectively,which may appear diferently at diferent occurrences.
2 Split Characteristics Least-squares Procedure
Introduce two function spaces
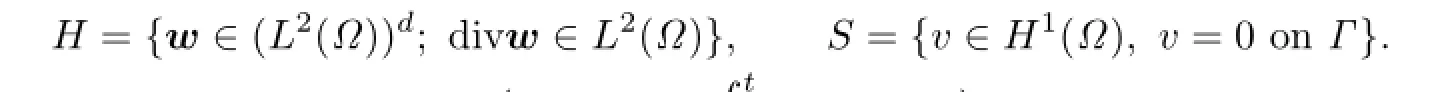
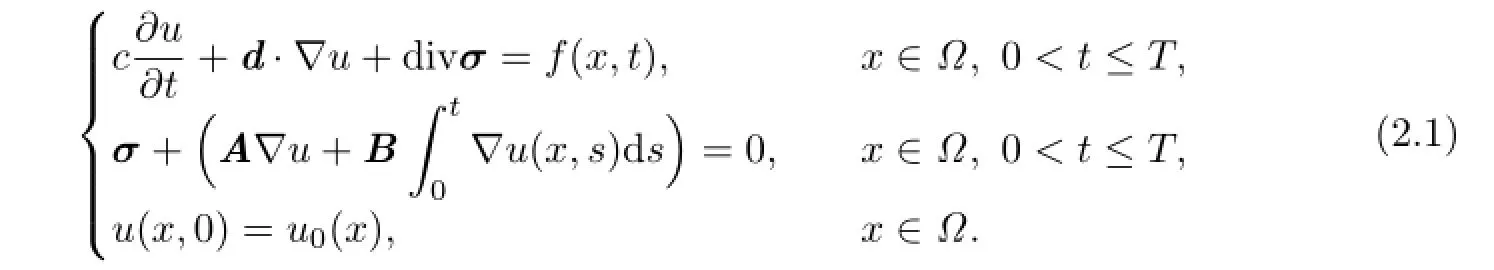
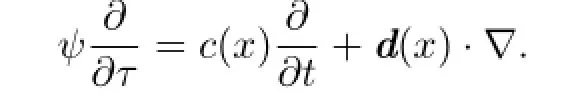
(2.1)can be put into the form
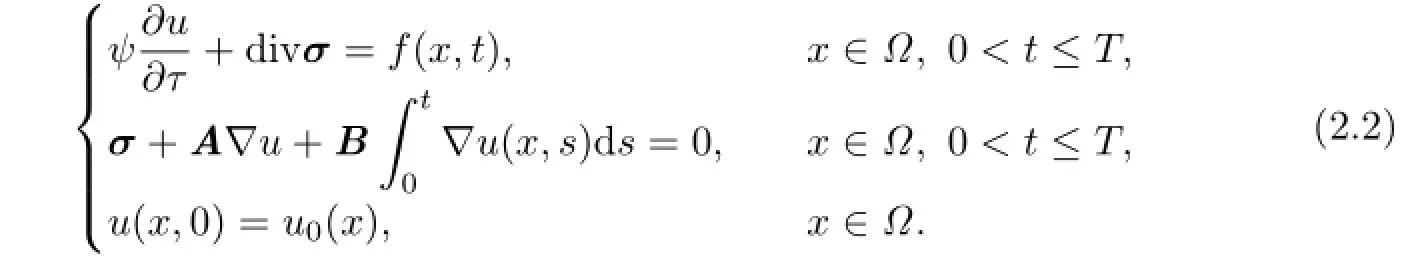
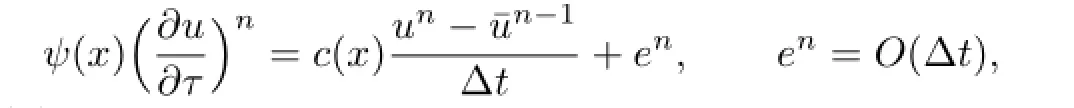
We can rewrite the system(2.2)as the following semi-discrete system:
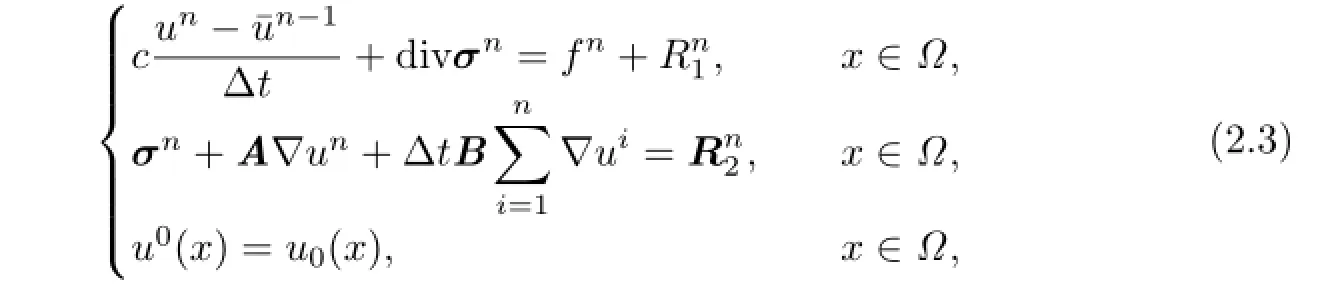
where
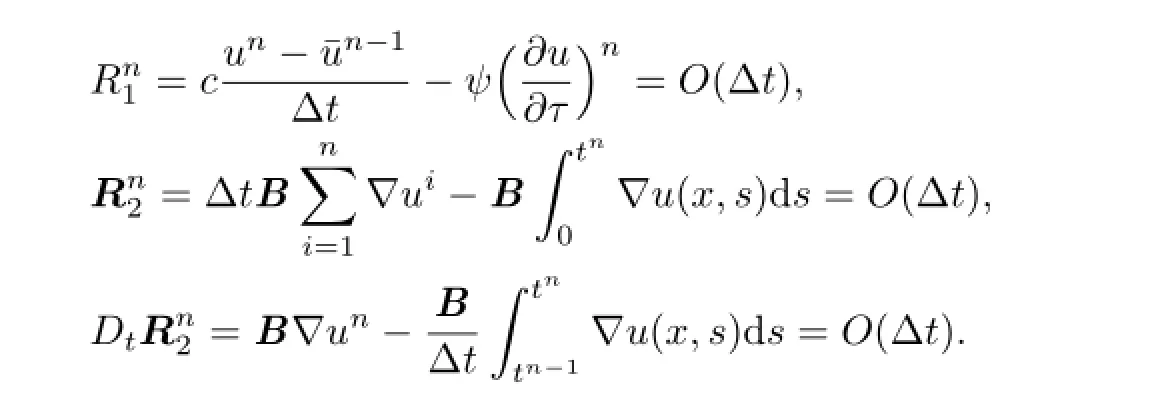
Equivalently we have that
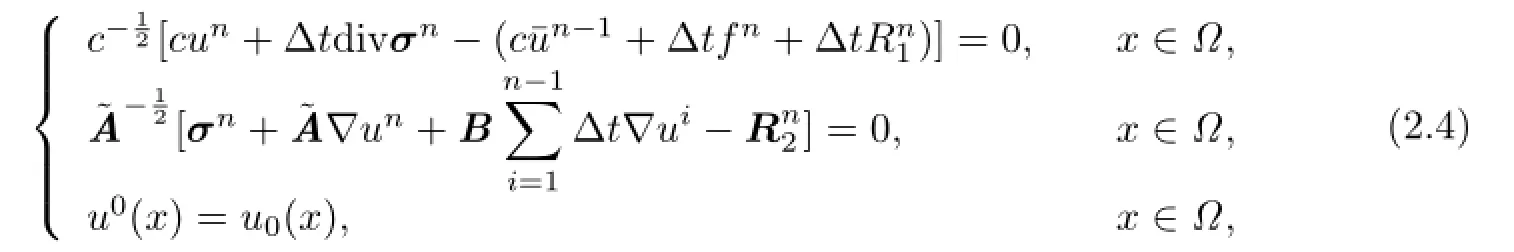
where~A=A+ΔtB.
Defne the minimization functionalas
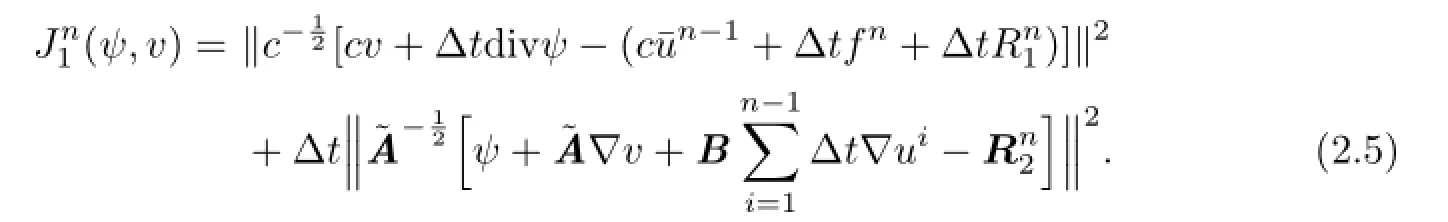
Then the least-squares minimization corresponding to(2.4)is:fnd(σn,un)∈H×Ssuch that
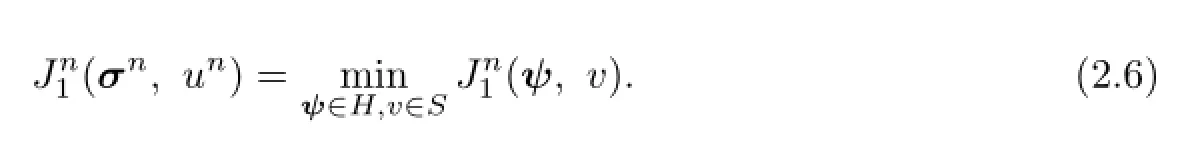
The weak formulation of(2.6)is:fnd(σn,un)∈H×Ssuch that
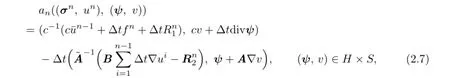
where the bilinear formanis defned as
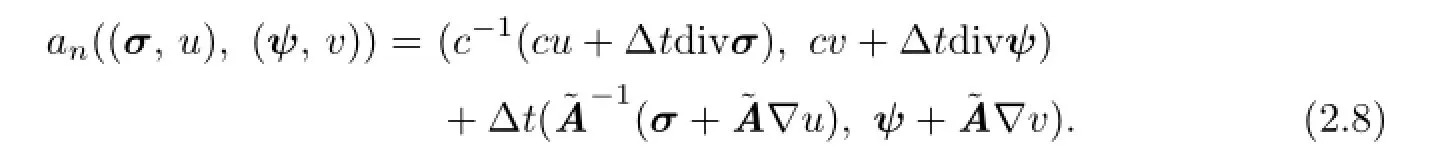
LetThσandThube two families of fnite element partitions of the domainΩ,which are identical or not.Lethσandhube mesh parameters.Based onThσandThu,we construct the fnite element spacesHhσ⊂HandShu⊂Swith the following approximation properties: there exist integersk≥0,l≥1 such that
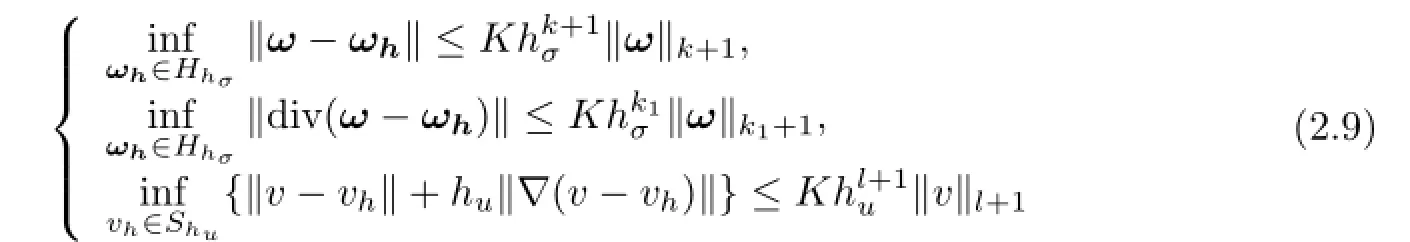
Omitting the time truncation error terms in(2.7),we defne the following least-squares procedure with the method of characteristics.
Scheme I.Given an initial approximationwhichis defned in Section 3,we seeksuch that
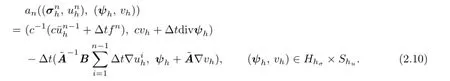
Remark 2.1Scheme I is still a conventional least-squares characteristic mixed fnite element scheme.Now we discuss the bilinear formanin the following lemma,which leads to a decoupled system.
Lemma 2.1For any(σ,u),(ψ,v)∈H×S,we have that
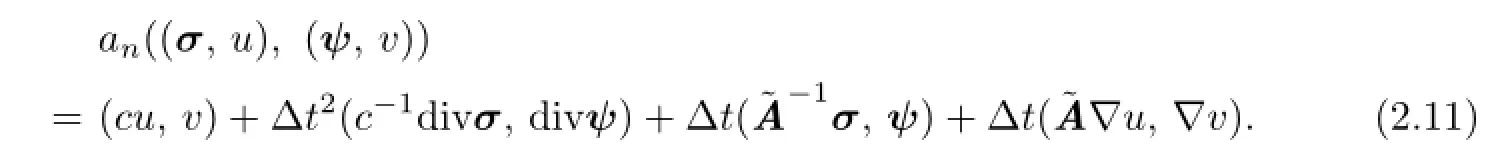
Proof.A direct calculation shows that
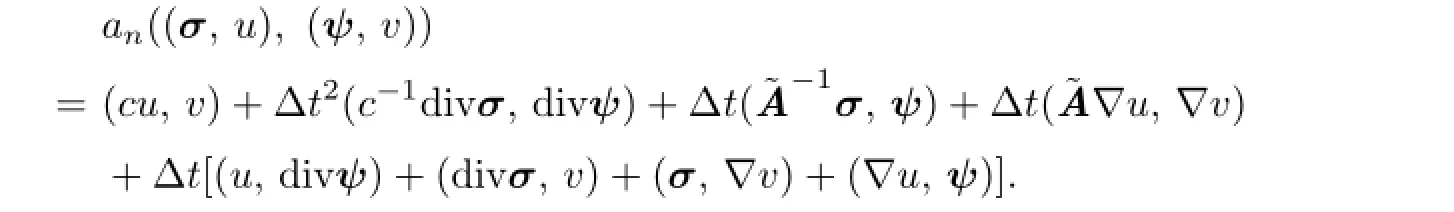
By applying Green’s formula we have
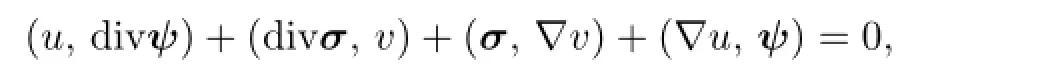
which completes the proof of(2.11).
Now,we can derive the split least-squares characteristic fnite element method.
Scheme I′.Letψh=0 andvh=0 in(2.10),alternatively.By using Lemma 2.1,we have the equivalent form of Scheme I
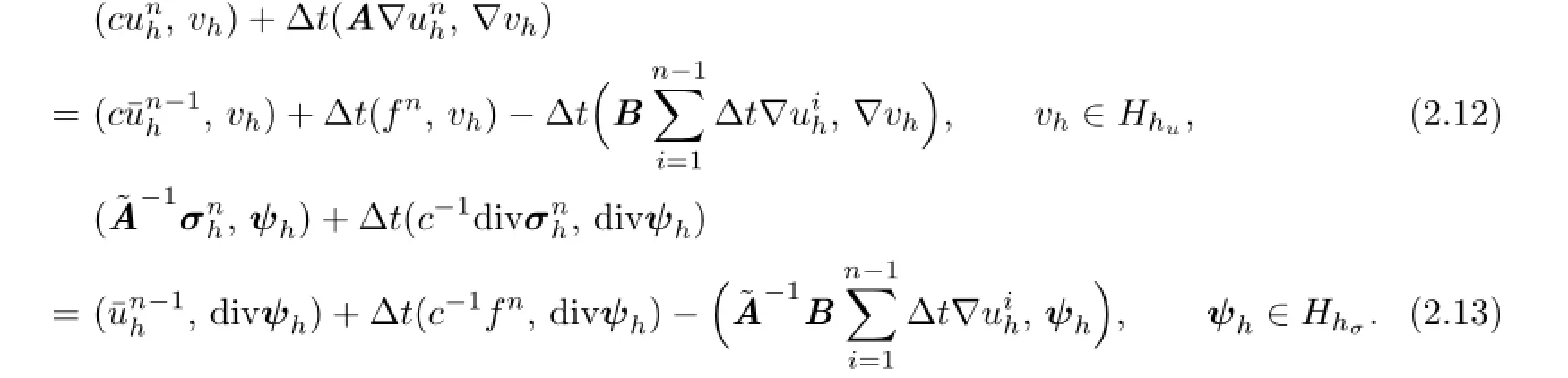
Remark 2.2It is obviously that Scheme I′is a process in whichuhandσhcan be solved separately.Moreover,the sub-procedure(2.12)is the same as a fully discrete Galerkin Characteristic fnite element procedure for the problem(1.1).
Remark 2.3Lemma 2.1 also tells us that the bilinear forman(·,·)is continuous and positive defnite inH×S.So it follows from Lax-Milgram theorem that Scheme I′has a unique solution.
3 Convergence Analysis
In this section,we analyze the convergence of the procedure.For this purpose we introduce some projection operators frst.
From the approximate property of fnite element spaces we know that there exists a vector-valued function Qσ∈Hhσsuch that
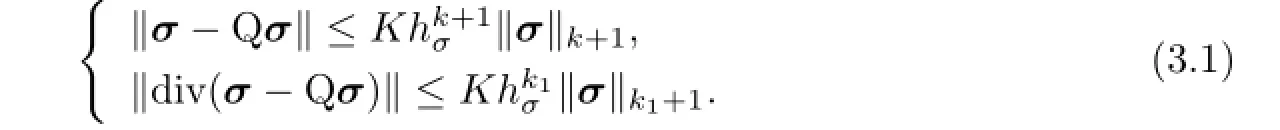
Forun∈S,we defne its elliptic projectionRun∈Hhusuch that
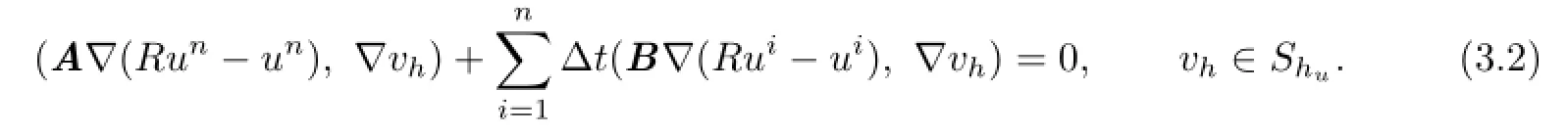
Lemma 3.1There exists a positive constant K independent of the discretization param-etersΔt,h
σand husuch that for s=0,1 {
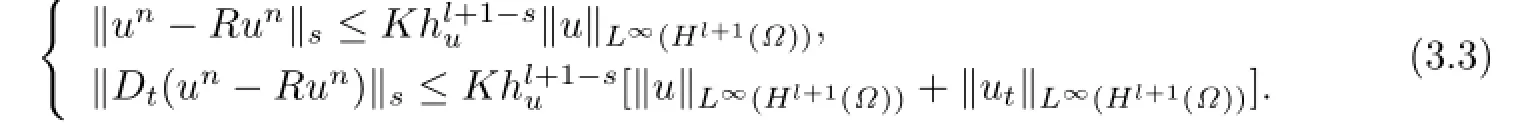
Lemma 3.2[3]Let q∈L∞(L2).Then

1and k2.
Lemma 3.3[3]If η∈L∞(L2)and¯η(x)=η(x-g(x)Δt),where g and g′are bounded,then

We are able to demonstrate our main result for the scheme.
Theorem 3.1Let(σ,u)be the solution of(2.1)andbe the solution of Scheme
I′.Suppose that the solution of(2.1)has regular properties that u,ut∈L∞(Hk+1),σ=0,1,
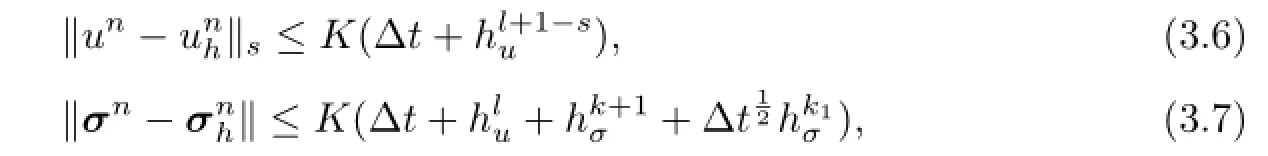
where the constant K is dependent upon T and some norms of the solution(σ,u),and independent of the mesh parameters hu,hσandΔt.
Proof.We prove(3.6)frst.Lettingψ=0 in(2.7)and using Lemma 2.1,we have
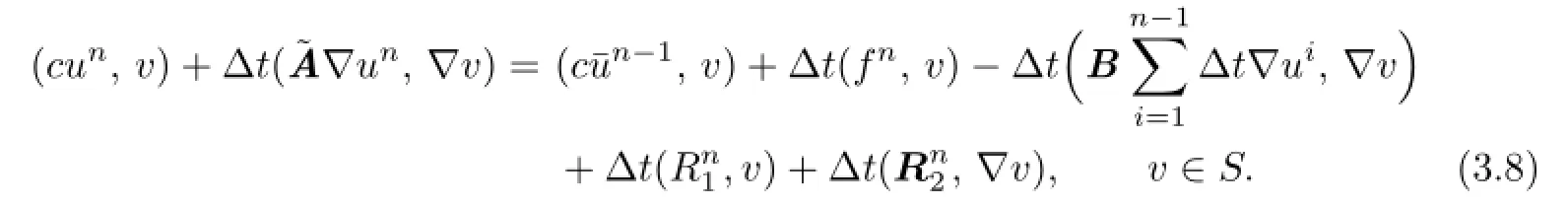
Subtracting(3.8)from(2.12),we obtain
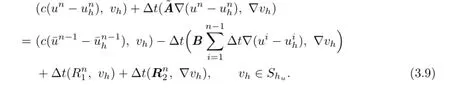
Writeun-unh=un-Run+Run-unh=ρn+θn.Since the estimates ofρnare known, we need to fnd only the estimates ofθn.From(3.9)we see thatθnsatisfes the following error equation
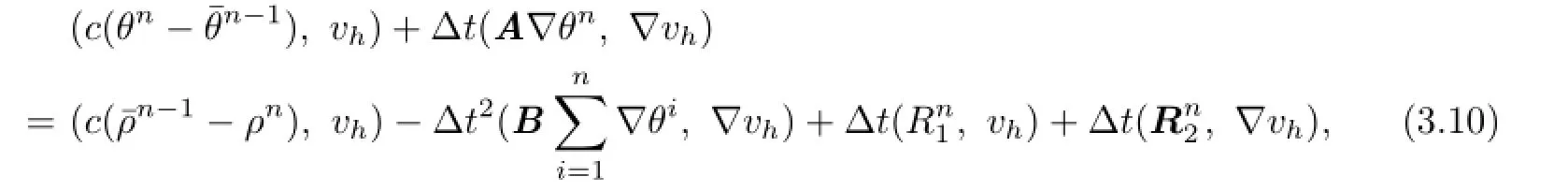
where we have used the equation
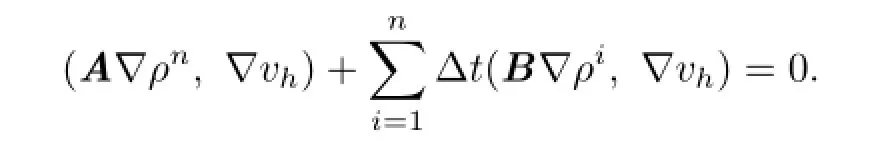
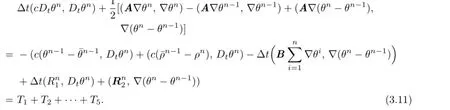
Settingin(3.10),we have
Using Cauchy’s inequality,we estimate(3.11)term by term.
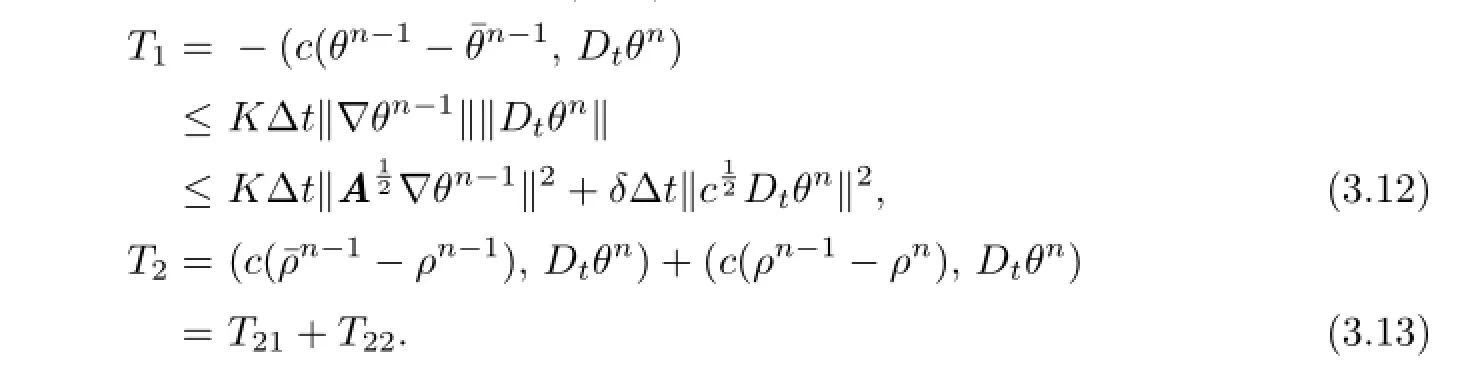
From Lemmas 3.2 and 3.3,we have
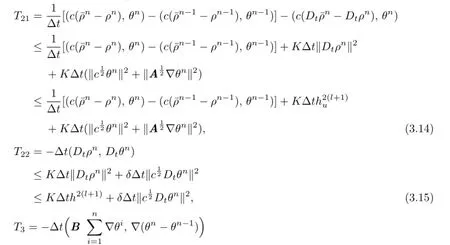
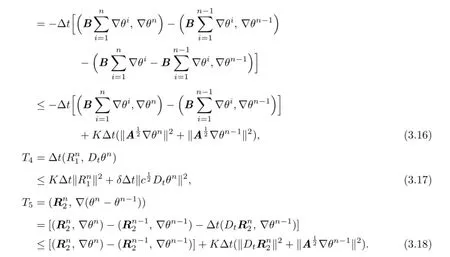
Therefore,combining these estimates,we can obtain
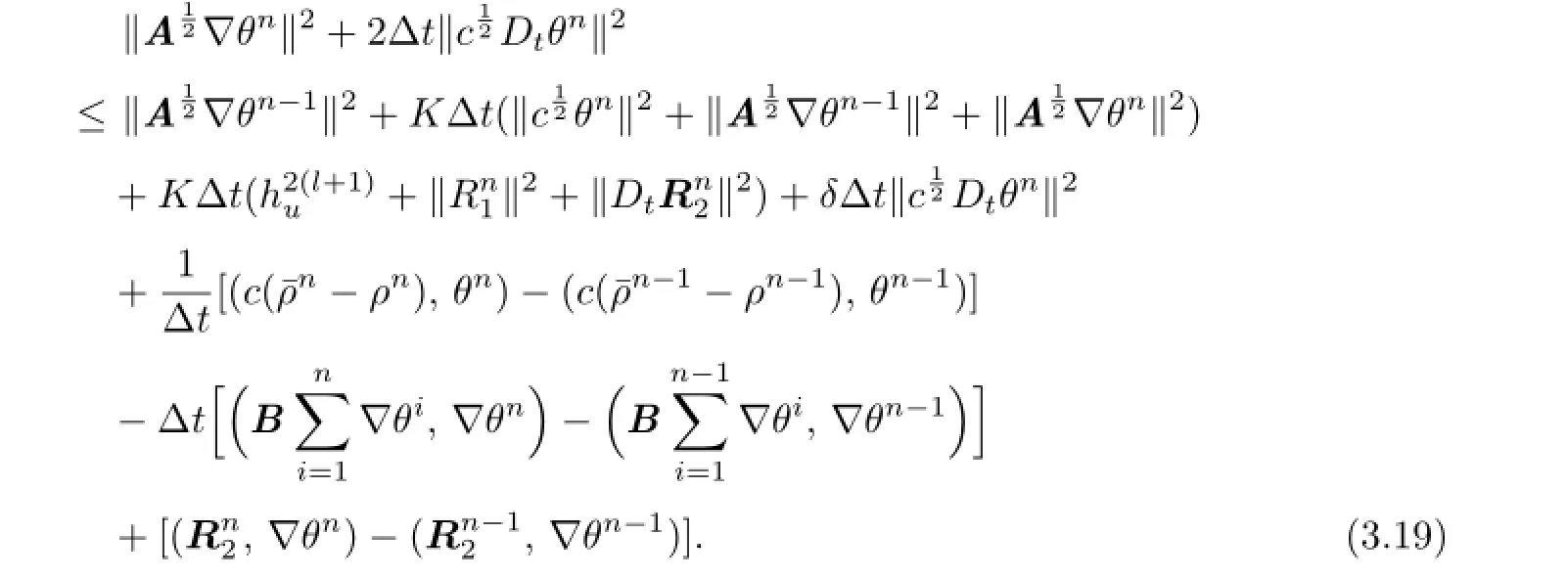
Summing(3.19)fornfrom 1 toJ,we have
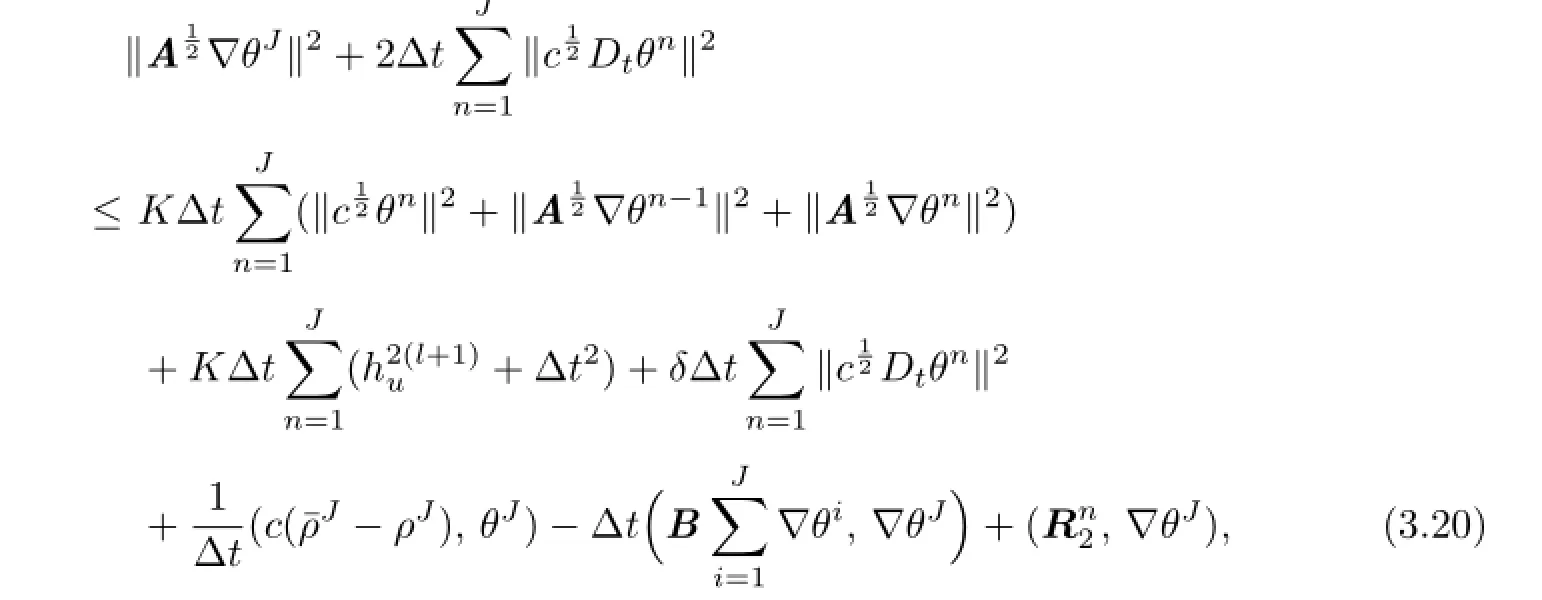
where we have applied the initial approximation
From Lemmas 3.2 and 3.3,we have
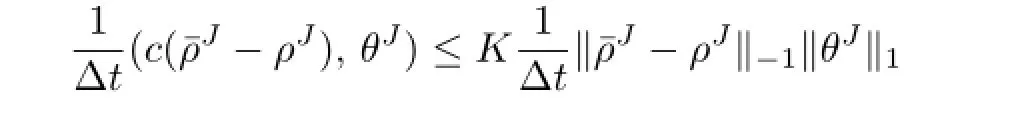
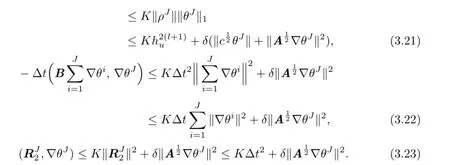
Applying(3.21)-(3.23),we obtain
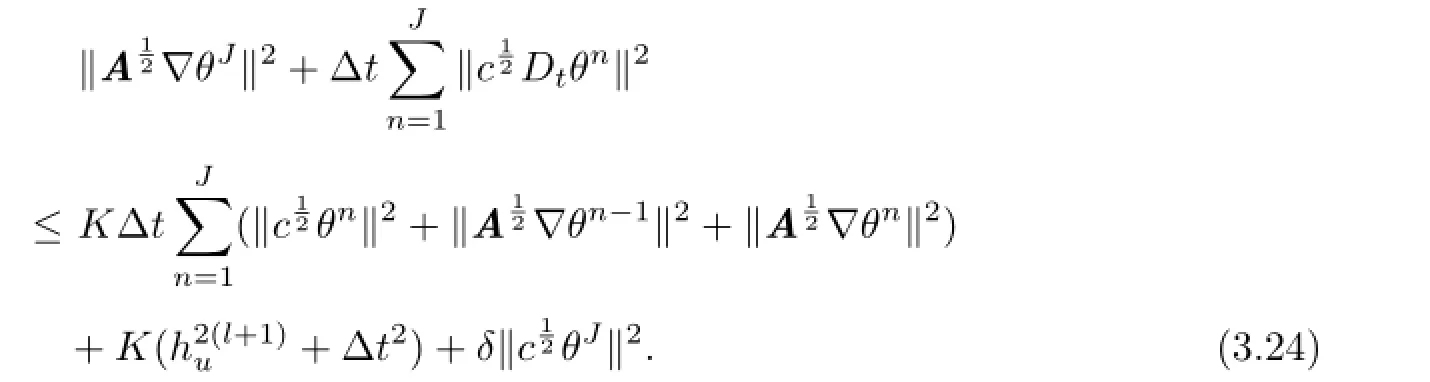
Applying a known inequality
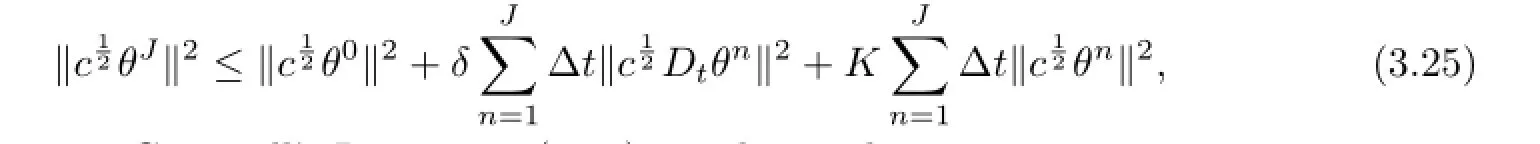
and the discrete Gronwall’s Lemma to(3.24),we derive the estimate

Noticingwe are able to demonstrate(3.6).Now we analyze the error estimate forσ.Lettingv=0 in(2.10)and using Lemma 2.1,we have
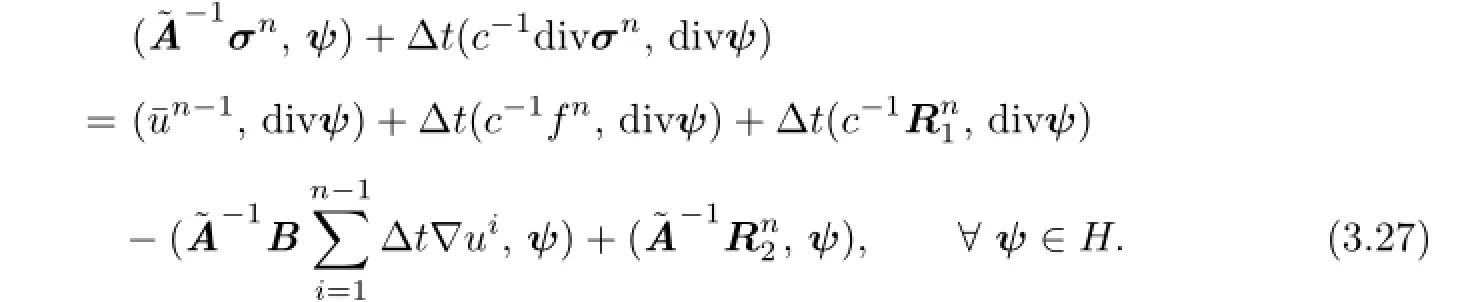
Let.Subtracting(3.27)from(2.13),we see thatπnsatisfes the following error equation
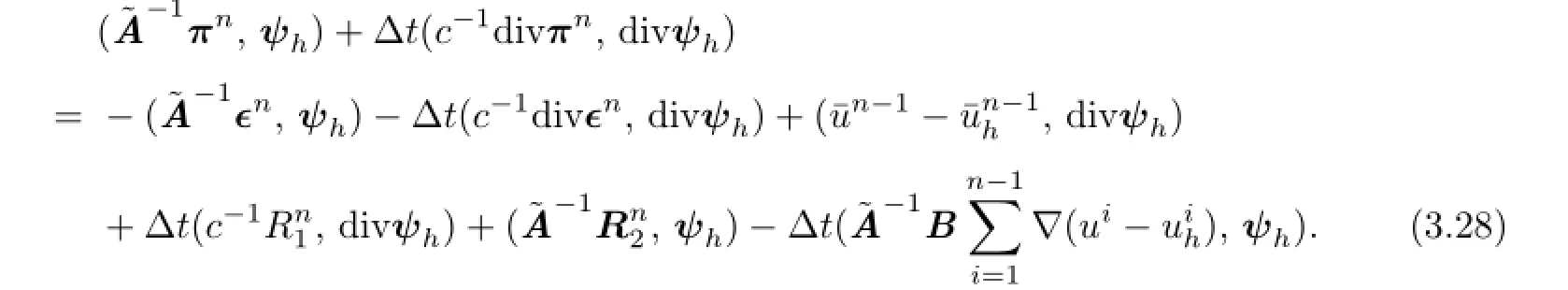
Settingψh=πnand using Cauchy’s inequality and Lemma 3.2,we have
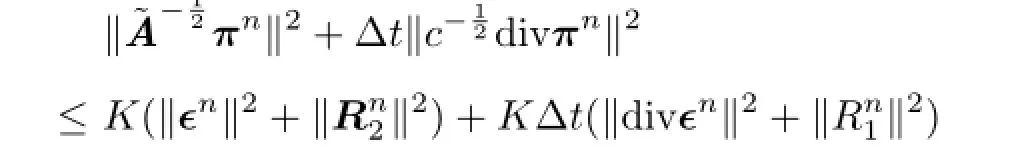
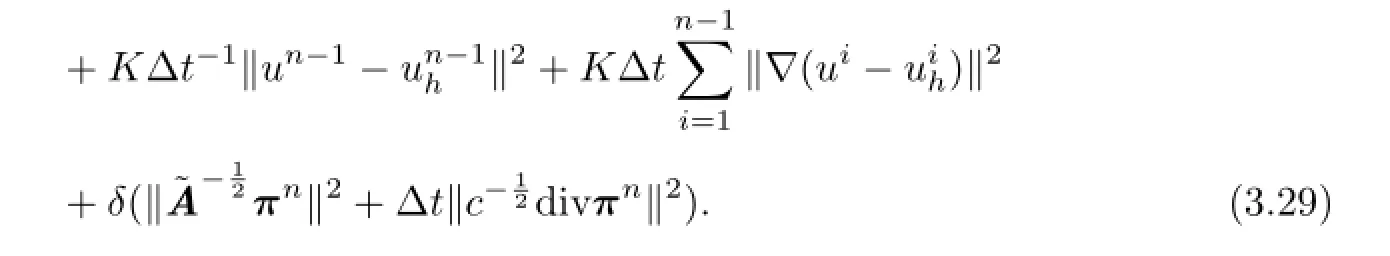
Therefore
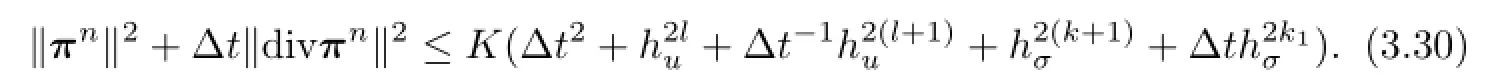
Hence,by using(3.1)and the triangle inequality,we are able to demonstrate(3.7).The proof of Theorem 3.1 is completed.
From Theorem 3.1,we see that the method leads to the approximate solutions with accuracy optimal inH1andL2norms foruand sub-optimal in(L2(Ω))dnorm forσ.The method is reasonable for such problem.
4 Numerical Example
In this section,we carry out the numerical example to demonstrate the theoretical results. Consider the model equations
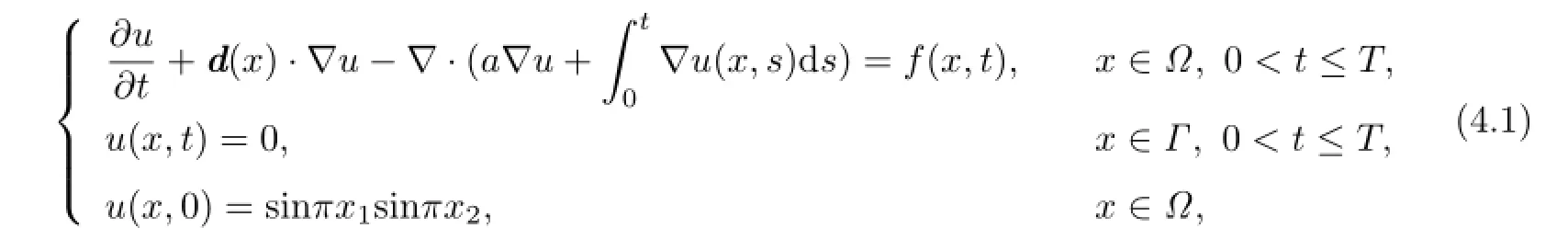
whereΩ=(0,1]×(0,1],a=10-3.The exact solution is chosen to beu=etsinπx1sinπx2, and the source termf(x,t)is determined by the above data.
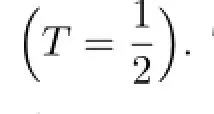
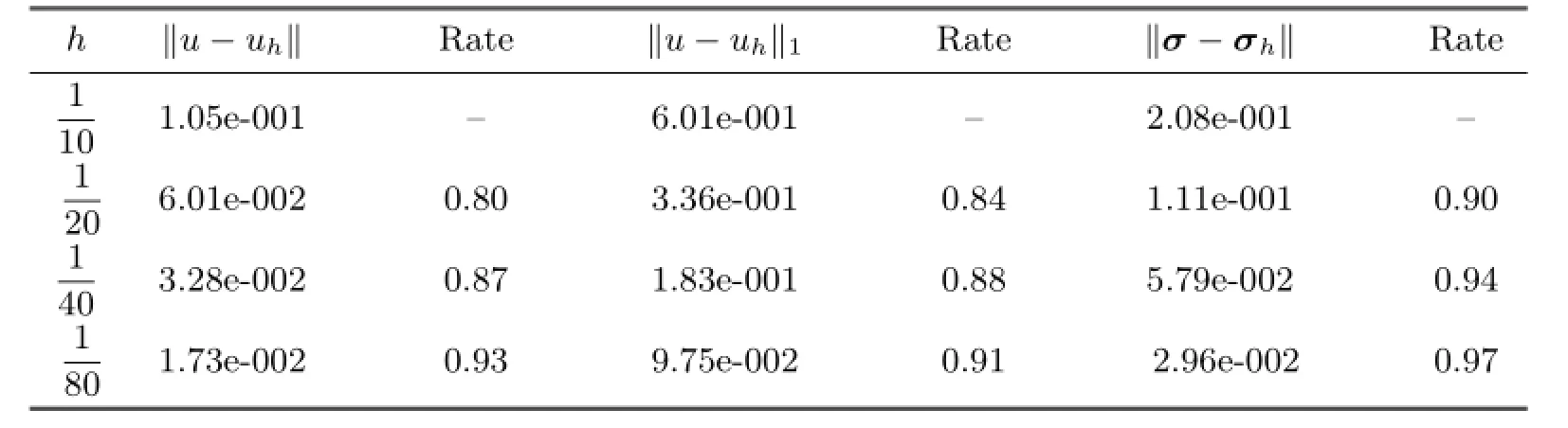
Table 4.1 The numerical results for Scheme I′
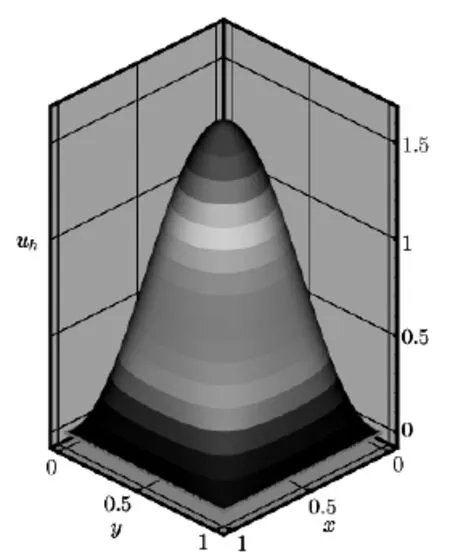
Fig.4.1 The approximate solutionuh
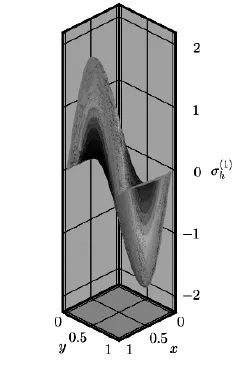
Fig.4.2 The approximate solution
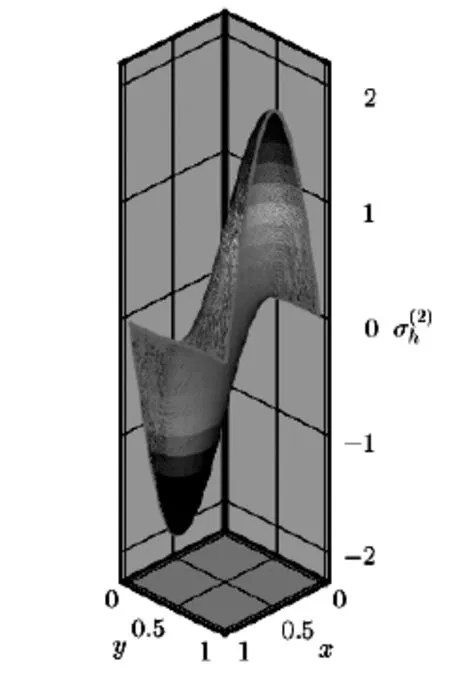
Fig.4.3 The approximate solution
5 Conclusion
We derive a split least-squares characteristic procedure for convection-dominated parabolic integro-diferential equations in this paper.The resulting procedure can be split into two independent symmetric positive defnite sub-schemes,and they are not subject to the LBB consistency condition.We have proved the method yields optimal estimates in the corresponding norms.Numerical experiments are given to confrm the efciency of the scheme.
6 Appendix-Proof of Lemma 3.1
We frst prove the frst inequality in(3.3).The proof of the second one is similar.It is clear that whenn=0,(A∇(Ru0-u0),∇vh)=0.It is clear that the projection operatorRu0is the orthogonal elliptic projection operator,then the following inequality holds(see[15]):
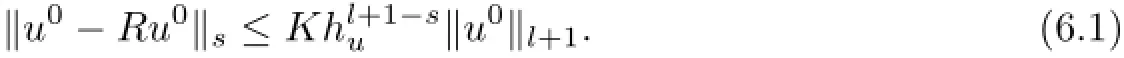
Letπhun∈Shube the interpolant ofun.From the defnition we have
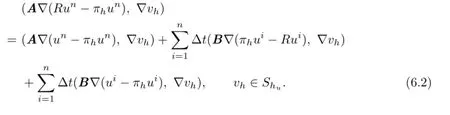
Letting,we have that
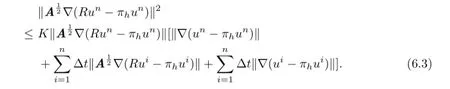
Therefore
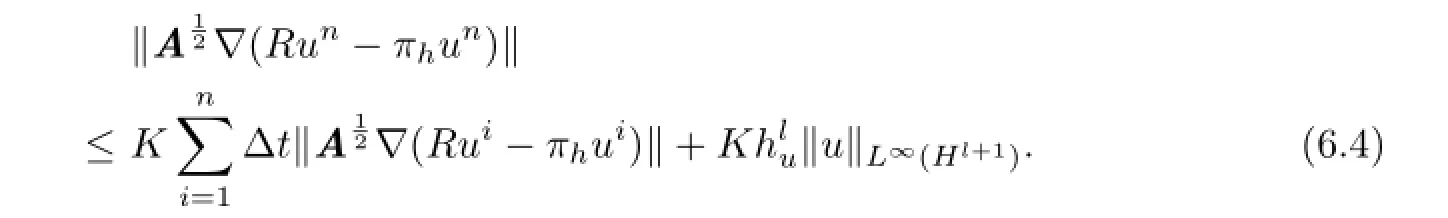
Gronwall’s inequality shows that
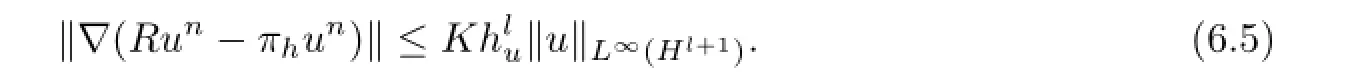
Combining with the estimate ofcompletes the proof of the frst inequality withs=1.
Now we estimate.For this purpose we defnewsatisfying
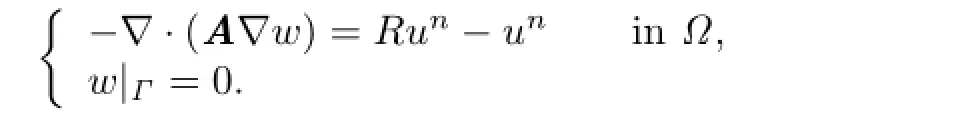
By using theH2-regular assumption we have that

Now we consider‖Run-un‖.Direct calculation shows that
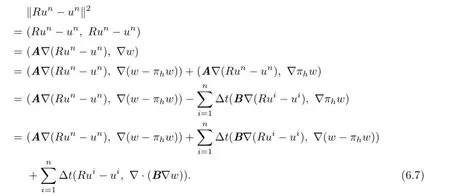
Therefore
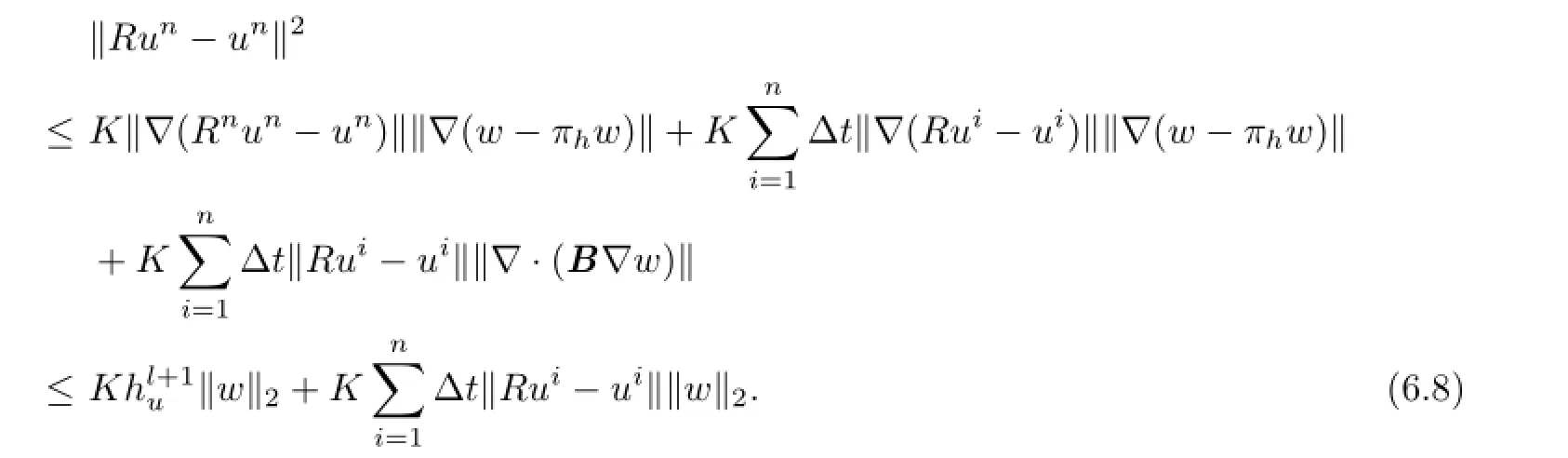
Noticing(6.6),we have
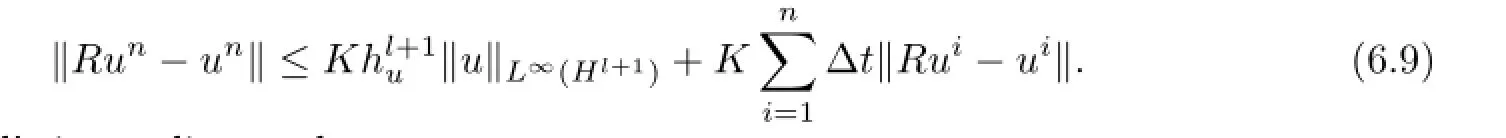
By Gronwall’s inequality,we have
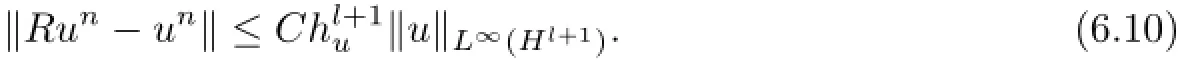
The proof of the second inequality is similar.
[1]Allegretto W,Lin Y,Zhou A.A box scheme for coupled systems resulting from microsensor thermistor problems.Dyn.Contin.Discrete Impuls.Syst.,1999,5:209-223.
[2]Cushman J H,Hu X,Deng F.Nonlocal reactive transfer with physical and chemical heterogeneity:Localization error.Water Resource Res.,1995,31:2219-2237.
[3]Douglas J,Russell T F.Numerical methods for convection-dominated difusion problems based on combining the method of characteristics with fnite element or fnite diference procedures.SIAM J.Numer.Anal.,1982,19(5):871-885.
[4]Ewing R E,Russell T F,Wheeler M F.Convergence analysis of an approximation of miscible displacement in porous media by mixed fnite elements and a modifed method of characteristics.Comput.Methods Appl.Mech.Engrg.,1984,47:73-92.
[5]Guo H.Least-squares Galerkin procedures with the method of characteristics for convectiondominated parabolic integro-diferential equations(in Chinese).Chinese J.Engrg.Math.,2004,21(6):979-983.
[6]Ladyzhenskaya O A.The Mathematical Theory of Viscous Incompressible Flows.London: Gordon and Breach,1969.
[7]Babuˇska I.The fnite element method with lagrangian multipliers.Numer.Math.,1973,20: 179-192.
[8]Brezzi F.On the existence uniqueness and approximation of saddle point problems arising from Lagrangian multipliers.RAIRO Mod´el.Math.Anal.Num´er.,1974,8:129-151.
[9]Rui H,Kim S,Kim S D.A remark on least-squares mixed element methods for reactiondifusion problems.J.Comput.Appl.Math.,2007,202:230-236.
[10]Rui H,Kim S D,Kim S.Split least-squares fnite element methods for linear and nonlinear parabolic problems.J.Comput.Appl.Math.,2009,223:938-952.
[11]Duran R E.On the approximation of miscible displacement in porous media by a method of characteristic combined with a mixed method.SIAM J.Numer.Anal.,1088,25:989-1001.
[12]Adams R A.Sobolev Spaces.New York:Academic Press,1975.
[13]Raviart P A,Thomas J M.A Mixed Finite Element Method for 2nd Order Elliptic Problems, Mathematical Aspects of Finite Element Methods:Lecture Notes Math.vol.606.Berlin: Springer,1977:292-315.
[14]Nedelec J C.Mixed fnite element inR3.Numer.Math.,1980,35:315-341.
[15]Ciarlet P G.Finite Element Methods for Elliptic Problems.New York:North-Holland,1978.
[16]Wheeler M F.A prioriL2error estimates for Galerkin approximation to parabolic partial diferential equations.SIAM Numer.Anal.,1973,10:723-759.
A
1674-5647(2015)01-0001-14
10.13447/j.1674-5647.2015.01.01
Received date:May 17,2012.
Foundation item:The NSF(11101431 and 11201485)of China and the NSF(ZR2010AL020)of Shandong Province.
E-mail address:sdugh@163.com(Guo H).
2010 MR subject classifcation:35L15,65M15,65M60
杂志排行
Communications in Mathematical Research的其它文章
- Weak Convergence Theorems for Nonself Mappings
- Existence of Solutions for a Four-point Boundary Value Problem with a p(t)-Laplacian
- Strong Convergence for a Countable Family of Total Quasi-ϕ-asymptotically Nonexpansive Nonself Mappings in Banach Space
- Equivalent Conditions of Complete Convergence for Weighted Sums of Sequences of Extended Negatively Dependent Random Variables
- A(k,n-k)Conjugate Boundary Value Problem with Semipositone Nonlinearity
- Derivative Estimates for the Solution of Hyperbolic Afne Sphere Equation
