基于TSC-RBF的水质预测方法——以漓江阳朔河段为例

李 景 文，王 珂，殷 敏，刘 华 尧，王 翰 钊

（1.桂林理工大学测绘地理信息学院／广西空间信息与测绘重点实验室，广西 桂林 541004；2.广西有色勘察设计研究院，广西 南宁 530031；3.郑州测绘学校，河南 郑州 450015）

随着GIS分析方法的快速发展和空间分析推理的要求越来越高，地理信息预测成为空间数据分析的重要方面。传统的信息预测方法有自回归分析法［1］、灰色预测法［2］、组合预测方法［3］等，主要是从地理实体的空间信息出发，但地理实体的信息具有时间、空间与属性复合时空特征（Temporal-Spatial Characteristics，TSC），如何将地理实体的空间、属性与时间有机结合，将知识推理与GIS结合实现对未知信息的推理是地理信息预测的难点之一。本文充分利用神经网络方法的强大自组织学习能力、大规模并行处理能力、优异的非线性映射能力和好的容错性等特性［4，5］，结合地理实体复杂的时空特征，采用径向基函数（Radial Basis Function，RBF）神经网络方法对地理实体数据隐含的规律进行分析，构建了一种基于TSC-RBF神经网络的水质信息预测模型。

1 RBF网络推理算法原理

人工神经网络以所需精度逼近任意非线性连续函数，这种特性适用于复杂系统的模拟和分析计算领域。设典型多层神经网络（图1）输入层的输入空间为m0维，隐藏层的空间为m1维，输出层的输出空间为m2维，从输入层到输出层映射的完整表达为：

推理过程选择一个径向基函数（RBF）：

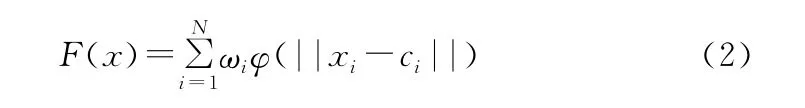
图1 多层神经网络结构Fig.1 Multilayer neural network structure

式中：φ（｜｜xi－ci｜｜）称为径向基函数，是N个任意函数的集合，｜｜·｜｜表示范数，通常为欧几里得范数，ωi为F与φ的内积，即F为ωi与φ的线性组合逼近。由于φ（｜｜xi－ci｜｜）是非负的对称函数，ci为φ的中心，求函数在未知点的值相当于函数的插值。通过F，RBF网络可以实现从隐藏层到输出层的线性映射，同时降低向量维数。

RBF网络有多种学习算法，本文采用最小二乘的RBF网络训练方法。用回归模型实现的RBF网络映射为：

写成矩阵形式，即：

式中：y是期望输出向量，e是期望输出与实际输出的误差向量。

通过Gram-Schmidt正交化［6］方法将矩阵Φ分解为：

式中：A是一个主对角线为1的上三角阵，U是具有相互正交列ui的矩阵，使得：

式中：g＝Aω，期望输出向量t表示成矩阵U的相互正交列的线性组合，坐标向量g的最小二乘解为：

由此，回归向量gi的分量与RBF中心ci相互对应，在求和中反映每个RBF中心的作用。可得第p个RBF中心误差缩减率为：

通过前向回归方式的RBF中心选择提供一个简单有效的标准，在前向回归的每一步中，选择一个RBF中心使误差的缩减率为最大。

2 地理实体的标准化处理

漓江流域的水质情况一直受到重视。但通过对漓江流域饮用水源地的监测结果发现：干流水质较好，而支流污染较为严重；氨氮、总大肠菌群、细菌总数等项目都有超标的情况，因此，加强漓江水体污染的监测和预防必不可少。其中《地表水环境质量标准》（GB3838－2002）中规定水温、p H值、溶解氧、氨氮、总磷、总氮、铜等共24项作为我国水质评价的基本项目。水质指标表达了水中的某一种或某一类物质的含量，反映了水质的好坏。例如p H值反映了水中各种溶解性化合物达到的酸碱平衡状态，主要是二氧化碳、碳酸氢盐、碳酸盐的平衡等。水温与水中物理性质、化学反应和生物化学反应有着密切的关系，也是引起其他水质指标发生变化的主导因素。本文以环境部和桂林市环保局公布的阳朔下游采样点处近三年每周水体CODMn和NH3－N的含量数据作为样本实例，并将其作为预测样本。

水质信息的数据复杂且种类、单位、数量级等参数不同，例如河水的径流量和水体中的p H值，从数量级上考察，两者之间差距较大，若同时放在一个模型中进行分析，会产生较大误差，并影响推理预测的准确性。因此，为了简化计算，需要对原始数据进行标准化处理，本文选择正切函数为传递函数，正切函数的输出值y∈（0，1），且只有当输入为－∞，＋∞时，输出值等于0或1。首先获取原始数据的最大值和最小值，取两者之和再乘以2得到一个标准参数。再将同个属性字段全部原始数据和这个标准参数相比得到的比值（消除了不同种类数据间的数量级的差距）视为一个标准化处理后的值，输出范围为0.1～0.6，便于神经网络训练。公式如下：

式中：zij为原始数据的标准化值，xij为原始样本值，xmax、xmin分别为原始数据中的最大值和最小值。水质信息的原始值及标准化值如表1所示。

标准化后的数据只是一个比值，并不具备现实意义，所以推理结束后需对其进行标准化系数反计算，公式如下：

3 地理实体时空数据的一体化表达

3.1 时空特性（TSC）的一体化组织

用M作为地理实体的符号表达，地理实体的空间、属性、时间信息可表达为一个数组：

式中：S为实体M的空间数据集合，表达点、线、面和坐标等点集合，R为属性信息集合，T为采集取样的时刻集合。在数据推理的过程中，地理实体由空间、属性、时间3种大类的数据的数学集合来模拟：空间数据使用其坐标值或经纬度和高程（L，B，H）来记录；地理实体的每一种属性都作为属性列对其进行记录；时间以Hermann Minkowski时空维中的时间轴来记录，表示从过去延伸到未来的线性参数，作为考察地理实体空间、属性信息变化的参考。

由于地理实体的空间特征、属性特征和时间特征的描述方法和数据组成不同，本文采用空间矩阵的形式对地理实体进行格式化处理。

将地理实体的时空特征视为一个多维空间：空间特征由实体的三维空间坐标表示，即（L，B，H）；地理实体空间特征的格式化方法以地理实体空间特征描述地理实体空间信息采样点，以坐标记录其空间采样点p的数据组织矩阵形式如下：

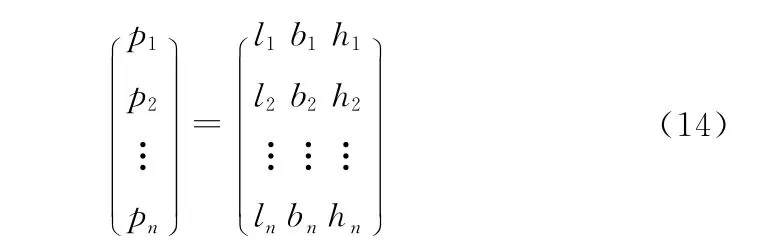
3.2 时空数据超曲面的构建

在地理实体数据建模过程中，需要对时空数据进行一体化拟合组织。时空流形拟合的过程变换为在高维空间中寻找一个能够对输入数据进行优化拟合的曲面Γ［7－10］。

设在n维空间中，Γ满足方程：

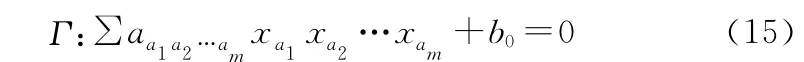
式中：ai＝（1，2，…，r；1≤i≤m）的点集合称为代数一体化，x＝（xa1，xa2，…，xam）∈Rn为一体化输入向量。

在时空数据进行超曲面插值时，时空数据的格式化表达为：

由于不同的时刻地理实体的属性特征不同，所以时间和属性数据需要同步记录，地理实体属性维度和时间维度多元组的矩阵描述可表示如下：

由式（13）得到地理实体属性和时间维度的格式化表达形式：

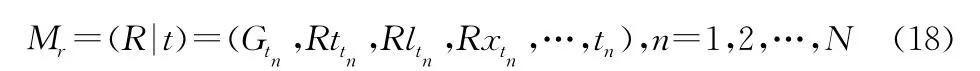
结合式（16）和式（18）时空数据的格式化描述，可表示如下：

每一个地理实体各个时刻的多元组转化为一个独立数值型向量，进而与欧式空间中流形超曲面的定义结合，构建时空数据超曲面。

对组织的地理实体数据作如下映射：

将每一个地理实体各个时刻的多元组都作为代数一体化的一个独立输入向量，每个元素则可理解为一体化的输入参数。M中全部为地理实体的数值型数据，取值范围为任意实数R。则映射得到的新多元组x＝（x1，x2，…，xp）∈Rn，结合式（20），可得时空一体化：

式中：（ωi，ωi，j，…，ωi，j，…，p）为训练学习后重新确定的权值，（x1，x2，…，xp）为一体化的流动坐标。

当某一流动坐标xk对最后的预测结果不产生影响时，如对于监测点固定形式，其高程等特征是恒定不变的，对推理不会产生影响，则可以将其权值赋0值，从而简化数据的结构。

4 基于TSC-RBF的信息预测推理验证

本文根据推理过程中的样本选择和RBF网络推理算法，选用CODMn和NH3－N作为推理项目，选择与CODMn和NH3－N相关的监测点监测信息作为样本数据，建立推理机制。使用环境部和桂林市环保局公布的阳朔采样点、大河乡采样点近三年每周水体CODMn和NH3－N数据为例，对下游阳朔采样点的2011年第2季度的水质情况进行模拟推演分析。实验选取2009年、2010年、2011年1季度的阳朔采样点数据及大河乡采样点的时空数据作样本空间［11］，利用基于地理时空特征的RBF时空数据推理方法对该地区的空间、时间和水质数据进行仿真推理实验，并依次推演出第2季度阳朔采样点的CODMn和 NH3－N数据。

推理过程分为推理预处理阶段、推理RBF网络拟合阶段和推理阶段。其中，E为推理机中间过程样本的输出误差，ε为期望输出误差，E＜ε为推理拟合的判定条件。

（1）推理预处理过程：①分析断面对CODMn和NH3－N有影响的参数。在推理目标的河流体系中，对CODMn和NH3－N产生影响的主要因素有：监测点的断面水体径流量Wq、数据采集时刻的断面水体温度Tem、河流溶解氧值Do、pH值等。②根据步骤①的采样信息及已有数据库中存有数据的相关程度和时间点的数量，确定RBF神经网络的拓扑结构。确定所有输入参数的空间位置用（l，b，h）记录，并计算已知采样点，距离目标采样点的距离记作Disi。③获得的采样点的属性数据主要有Wq、Tem、Do、pH，选取时间序列上不同监测数据构成推理机RBF网络的输入向量。在本例中，监测断面的高程信息对结果产生的影响可忽略，故将输入向量（ltn，btn，htn）中的htn权记为0，样本集合简化为8维输入向量：根据式（20）可建立样本集合：

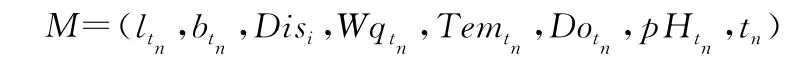
表2 CODMn的推理值Table 2 Inference value of CODMn mg／L

表3 NH 3－N的推理值Table 3 Inference value of NH3－N mg／L

为了更直观地表现基于时空特性的RBF神经网络推理情况，将表2、表3中推理值和实际值进行对比，如图2、图3所示。由图2、图3可以看出，基于时空特性的RBF神经网络推理结果较为准确，CODMn和NH3－N的推理值只有个别数据误差稍大，并且随着已知数据的不断增多和模型自身的不断学习匹配的过程，推理精度逐渐提高。

为了能评价和比较推理实验的结果，使用平均绝对相对误差mr、最大绝对相对误差mar、均方根误差rr3个性能指标对推理结果进行误差分析，各项推理误差指标比较见表4。

式中：yp（t）为数据推理值；yr（t）为数据的实际值。

表4 CODMn与NH 3－N值误差指标Table 4 Error index value of CODMn and NH3－N

通过误差分析，基于时空特性的RBF神经网络推理除了个别预测数据误差稍大，其他推理结果均较为准确，并且随着已知数据的不断增多和模型自身的不断匹配的过程，推理精度也会逐渐提高，能更准确地对具有时空特性的地理实体信息进行推理。

5 结论

基于神经网络的知识推理的应用已扩展到了众多领域，主要有模式识别与图像处理、信息预测与评价、自动控制等方面［12］。本文将RBF神经网络推理方法与地理信息的时空特征分析相结合，通过对RBF网络推理算法进行分析，将水质信息的时空一体化特性进行标准化处理，并通过水质信息中CODMn和NH3－N的含量推理数据验证了推理方法的可行性。基于TSC-RBF水质信息的预测推理方法既考虑了地理实体时空信息的复杂性，又充分利用RBF网络知识推理的优势，解决了异构数据建立数学模型的问题。通过实例分析结果，验证了基于时空特征的神经网络原理在进行信息推理时的可行性，为地理空间中其他复杂时空数据的预测与推理提供新的方法和思路。但是随着智慧城市的建设以及物联网的高速发展，对于解决多种地理时空信息的同时预测推理的方法需要进一步探讨。

［1］ 韦浩.多元回归分析法在滑坡空间预测中的应用 ——以耀州区为例［D］.西安：长安大学，2011.

［2］ 胡晓华，吉成儒，虞敏，等.灰色预测法的进一步推广及应用［J］.大学数学，2013，29（1）：117－121.

［3］ 孙兆兵.基于概率组合的水质预测方法研究［D］.杭州：浙江大学，2012.

［4］ 张艳秋.基于神经网络算法的知识获取研究［D］.南京：南京师范大学，2011.

［5］ 叶世伟.史忠植（译）.神经网络原理［M］.北京：机械工业出版社，2004.183－187.

［6］ 赵韬，姜金荣.分块 Gram-Schmidt正交化算法及其应用［J］.中国科学院研究生院学报，2009，3（2）：224－229.

［7］ HUNT N E.Phase Retrieval and Zero Crossing［M］.New York：Kluwer Academic Publisher，1989.

［8］ 王翰钊.基于RBF网络的地理实体信息推理方法研究［D］.桂林：桂林理工大学，2012.40－42.

［9］ 王翰钊.基于神经网络推理的GIS信息预测方法［J］.工程技术管理，2013（6）：53－55.

［10］ 李景文，王珂，叶良松，等.基于RBF神经网络的地理时空信息预测推理方法［J］.西师范大学学报，2014，12（4）：59－64.

［11］ 中华人民共和国环境保护部数据中心.全国主要流域重点断面水体环境质量自动监测周报［Z］.http：／／datacenter.mep.gov.cn／report／getCount Graph.do type＝run Qian Water.

［12］ 汪洋，李明峰，王芙蓉，等.基于3S技术与RBF网络的土地利用演变及预测［J］.南京工业大学学报（自然科学版），2008，30（3）：61－65.