基于形态滤波和动态测度的电能质量扰动检测

张 意，刘桂英，贾学瑞，吕 超

(长沙理工大学 电气与信息工程学院，湖南 长沙 4 10004)

基于形态滤波和动态测度的电能质量扰动检测

张 意，刘桂英，贾学瑞，吕 超

(长沙理工大学 电气与信息工程学院，湖南 长沙 4 10004)

针对电能质量扰动信号的检测与定位，详细分析了动态 (Dyn)测度的特点并在其对噪声较为敏感的基础上，构造一种双结构数学形态滤波器并结合Dyn测度算法实现电能质量扰动检测。对电网中的扰动波形进行预处理，以滤除信号中的随机噪声。对去噪后的信号波形，运用Dyn测度算法，通过提取信号的极值点获取信息从而快速识别信号的畸变点，对扰动起止时间进行检测。MATLAB仿真结果表明所提检测方法具有运算简单、运行速度快、检测准确的优点。

形态学滤波;动态测度;扰动检测;电能质量

0 引言

随着现代化敏感电力电子设备的大量使用和非线性负载的广泛应用，电能质量问题日益突出，它主要包括电压暂降/升、暂态脉冲和振荡［1］。为保证各类电气设备能正常、可靠运行，迫切需要采取相关措施改善电能质量［2－3］。电能质量扰动检测是治理和改善电能质量问题的基础，并逐渐成为电能质量分析领域研究的热点，进行扰动检测需要解决的主要问题包括信号的消噪和特征提取［4］。

在电能质量检测中，常用的方法包括傅里叶变换、小波变换法、数学形态学等。但傅里叶变换［5］在对工频稳态分量进行处理时，会大大削弱对畸变信号的检测能力，并且存在一个周波的延时和频谱泄露等缺陷，这无法满足现代电力系统的要求。小波变换法［6－7］是近年来逐渐兴起的一种方法，用小波变换可准确检测出扰动的位置，但其计算复杂、实时性不强，应用受到限制。数学形态学是一种基于积分几何和随机集论的非线性数学方法，其构成的形态滤波器提供了一种非常有效的非线性滤波技术，该滤波器较线性滤波器具有诸多的优越性［8］。文献 ［9］提出采用形态开－闭和闭－开滤波器平均组合的形式分别滤除白噪声和脉冲噪声。文献 ［10］采用多结构元素构造并行复合形态滤波器进一步改善滤波效果，相对于单结构形态滤波器滤波效果更好。文献［11］从波形畸变的角度出发，提出了一种基于动态测度的电能质量扰动实时检测方法，能快速检测信号极值点并识别信号的畸变点，有效检测多种电能质量扰动，但当信号受到噪声干扰时对检测结果影响较大。

本文基于数学形态学原理，构造一种双结构形态滤波器，提高滤波效果，对含有噪声干扰的信号进行滤波预处理，较好地保持原信号的基本特征，对滤波后的信号通过动态测度算法检测电能质量扰动的发生和终止时刻。

1 数学形态滤波的基本原理

1.1 数学形态学理论基础

数学形态学方法的基本原理，是利用预先设定好的结构元素来收集待处理信号的信息，通过在信号间不断移动，即可分析信号各分部之间的相互关系，从而提取出有用信息，达到抑制噪声的目的［12］。

在数学形态学中，利用腐蚀和膨胀分别来定义开运算和闭运算。开运算可以消除散点和毛刺即对图像进行平滑、过滤信号中的峰值噪声。闭运算可以填平小沟结构、抑制信号中的低谷噪声。

设输入序列f(n)是采样得到的一维多值信号，其定义域为F={0，1，2，3，… ，N－1};g(x)为预设的一维结构元素序列，其定义域为G={0，1，2，3，… ，P－1};其中 P和N为整数，且N≥P。则膨胀和腐蚀运算分别定义为

式中:n=0，1，…，N－1;x=0，1，…，P－1;⊕为膨胀运算;Θ为腐蚀运算。

由式 (1)形态开运算定义为

由式 (2)形态闭预算定义为

开闭运算都具有低通滤波器的特性，滤波效果和变换形式、结构元素的尺寸及形状有关。基于开、闭运算可以构建以下3种滤波算法:

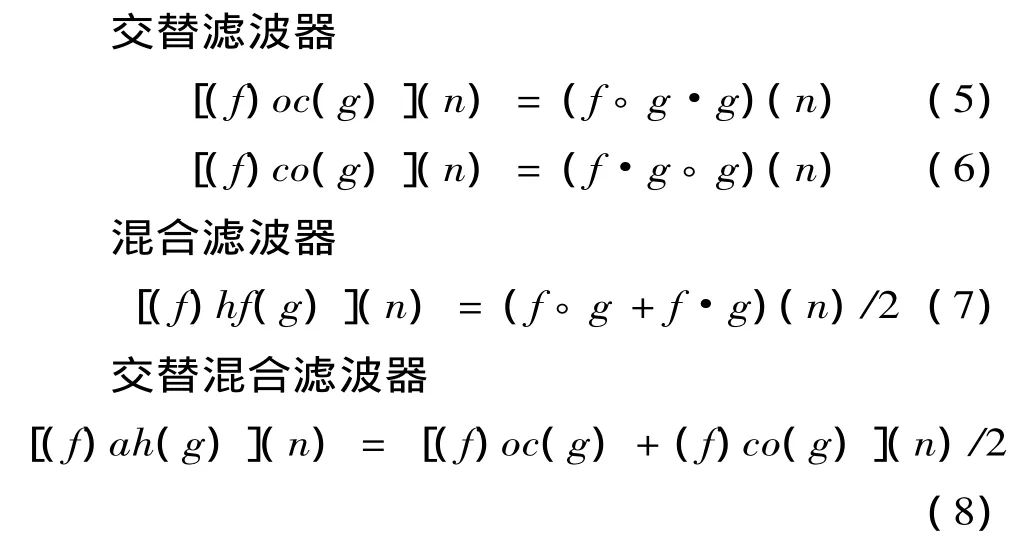
式中:oc为先开后闭的交替滤波运算;co为先闭后开的交替滤波运算;hf为混合滤波运算;ah为交替混合滤波运算。

当结构元素长度相同时，交替滤波器和混合滤波器计算速度相近，交替混合滤波器速度较慢，随着结构元素长度增加计算速度相差越大。由于开 (闭)运算的输出信号总是位于原信号的下(上)方，交替滤波器的输出会出现一定程度的偏移现象。为了解决这种现象，通常采用混合滤波器或交替混合滤波器对原信号进行滤波［13］。

1.2 构造数学形态滤波器

选取合适的结构元素是影响滤波器输出的主要因素，常用结构元素有余弦、半圆、三角、直线结构等。文献 ［14］针对电力系统中的常见噪声，通过数值仿真，对几种常用结构元素的滤波效果及计算速度进行了详细的对比分析。对于高频连续干扰、随机背景噪声，使用余弦结构元素滤波效果最好，且运算速度较快。对于脉冲噪声干扰，余弦和半圆结构元素都能有较好的效果，但半圆结构在计算速度上有优势。对于直流偏移量干扰，直线结构元素对其有提取作用。考虑到电网中噪声干扰的多样性和运算速度的快速性，本文采用双结构元素，余弦结构和直线结构元素的组合形式构成交替混合滤波器。其中g1为余弦结构元素，g2为直线结构元素，f1，f2分别为输入信号通过交替混合滤波器的输出，计算过程如图1所示。

图1 双结构交替混合滤波器

2 动态测度的原理和算法

法国学者M．Grimaud基于地形学提出了一种极值点评价测度方法——动态测度［11］，并成功应用于图像处理。由于Dyn测度能反映信号极值点的结构特征，并有效识别信号的畸变极值点，随后被引入电力信号分析领域以进行扰动检测。

基于动态测度的扰动检测方法，是利用电压或电流扰动信号畸变点的Dyn测度与信号波峰/谷的Dyn测度的差异进行扰动检测，二者测度差别较大，故可根据差异识别信号的畸变点。然后通过设定阈值舍弃信号波峰/谷点对应的Dyn测度，利用保留下的Dyn测度检测信号的畸变点。当信号中含有噪声特别是脉冲噪声时，会严重干扰Dyn测度检测从而无法有效识别畸变点。

设在极小值点M两侧有一个或多个低于点M的极小点，假设两侧分别存在最近的点为X1和X2，那么可以在M两侧找到两个与M等高的点N1和N2，则N1与M的路径动态测度即为N1与M之间的极大值中的最高点与M之间的高度差Dyn(N1)，同理可得 N2与M的路径动态测度 Dyn(N2)，如图2所示。极小值点M的Dyn测度等于两路径Dyn测度的较小值，即:

另一种情形是只存在一个最近的点N与M等高，那么极小值点M的Dyn测度为M与N之间极大值中的最高点与M之间的高度差，即:

当极小值点为最小值点时，其Dyn测度为信号最高点与最低点的高度差。同样，Dyn测度能识别极大值点。

图2 动态测度示意图

3 仿真实验分析

3.1 滤波仿真分析

为验证滤波效果，将文中滤波器与传统单结构形态滤波器进行比较，结合滤波后的波形图与信噪比分析。本文利用Matlab仿真软件生成扰动信号并进行仿真分析。设待处理信号是幅值为1的正弦电压信号，基波频率为50 Hz，信号长度为1 280个点。并叠加随机白噪声和脉冲噪声。本文滤波器选取余弦结构幅值为0.6，元素长度为28，直线结构幅值为0.1，元素长度为4。滤波效果如图3所示，其中图3(b)为采用直线结构元素的形态滤波器滤波效果图，其信噪比为42.015 6 dB，图3(c)为本文滤波器滤波效果，信噪比为53.439 7 dB。

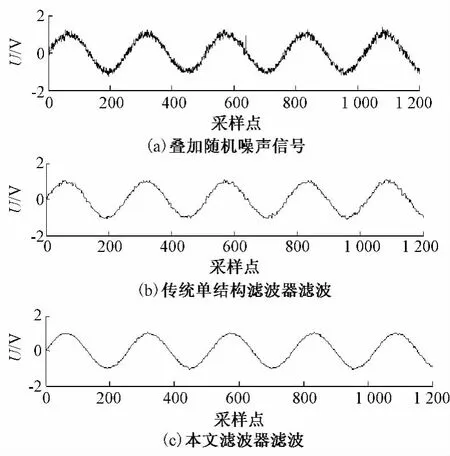
图3 滤波效果比较

由滤波仿真可知本文形态滤波器波形失真小，信噪比高，能较好地提取原始信号，滤波效果相对理想，对噪声起到有效的抑制作用，满足实验要求。

3.2 扰动检测实验

图4(a)是受到噪声干扰伴有电压暂降的原始信号波形图，未经滤波过程而采用Dyn测度法进行检测，取Dyn测度阈值为0.5进行分析，得到一系列Dyn测度，如图4(b)所示。发现因为受到噪声影响，检测到多个幅值接近的Dyn测度且分布点较为分散，这种情况下无法准确找出畸变点，检测结果误差较大。

图4 未消噪Dyn测度分析结果

为验证滤波后的Dyn测度检测效果，以电压暂降和暂态扰动为例进行扰动检测实验。图5(a)为幅值1 V的电压信号波形图，叠加随机白噪声和脉冲噪声并伴有50%的电压暂降。

图5 电压暂降分析结果

图6 暂态振荡分析结果

图6(a)为叠加随机白噪声和脉冲噪声的信号波形图，伴有暂态振荡，脉冲噪声在33 ms加入。采用本文滤波器对原始信号进行去噪，得到滤波后的波形分别如图5(b)、6(b)所示。结合动态测度方法，分别获取峰/谷点和畸变点的Dyn测度，合理选取阈值舍弃峰/谷点的Dyn测度，从而准确识别畸变点。

由图5(c)、5(d)可知，选取阈值大小为0.5。12.5 ms时刻出现了幅值为0.46的动态测，43.6 ms时刻出现幅值为0.42的动态测度，表明电压信号在上述两点发生畸变，即对应电压暂降的发生和结束时刻。由图6(c)、6(d)，24.6～29.4 ms之间出现连续幅值变化的动态测度，其中最大幅值为0.5，最小幅值为0.1，表明该时间段内有多个畸变点，对应暂态振荡的持续时间。仿真实验表明，将数学形态滤波与Dyn测度算法相结合能改善Dyn测度算法对噪声敏感的问题，从而提高电能质量扰动检测的精确性。另外，实测表明该方法对电压暂升、周期性扰动均有很好的检测效果。

4 结论

在没有噪声干扰的情况下，Dyn测度法能很好检测出扰动情况，针对该方法易受噪声的影响，本文构造了一种双结构形态学滤波器，能较好地去除扰动信号中的脉冲噪声和随机噪声，结合Dyn测度算法对电能质量扰动进行检测，提高了Dyn测度算法进行扰动检测的速度和准确性，弥补了Dyn测度算法易受噪声影响的缺陷。仿真结果表明，所提方法能在有效去除噪声干扰的同时准确检测出扰动的起止时间，是一种有效的电能质量扰动检测方法。

［1］徐立军，王维庆．用于改善暂态电能质量的用户电力技术的研究［J］．自动化仪表，2013，34(9):43－47．

［2］黄耀东，张颖，韩子骞．基于数学形态滤波的电压闪变检测研究［J］．电力科学与工程，2014，30(8):69－73．

［3］李燕楠，包广清．基于小波包和支持向量机的电能质量扰动识别［J］．电力科学与工程，2012，28(3):21－26．

［4］冯宇，唐轶，石延辉，等．电能质量分析与参数估计的研究方法综述［J］．电力系统及其自动化学报，2010，22(3):78－85．

［5］张斌，刘晓川，许之晗．基于变换的电能质量分析方法［J］．电网技术，2001，26(1):26－29．

［6］Karimi M，Mokhtari H，Iravani M R．Wavelet based on line disturbance detection for power quality applications［J］．IEEE Transactions on Power Delivery，2000，15(4):1212－1220．

［7］Mallat S，Hwang W L．Singularity detection and processing with wavelets［J］．IEEE Transactions on Information Theory，1992，38(2):617－643．

［8］王丽霞，何正友，赵静．基于数学形态学的电能质量扰动检测和定位［J］．电网技术，2008，32(10):63－68，88．

［9］岳蔚，刘沛．基于数学形态学消噪的电能质量扰动检测方法［J］．电力系统自动化，2002，26(7):13－17．

［10］赵春晖，孙圣和．一类多结构元素并行复合形态滤波器［J］．哈尔滨工业大学学报，1997，29(2):64－67．

［11］刘应梅，白晓民，张红斌，等．基于动态测度的电能质量扰动检测［J］．中国电机工程学报，2003，23(10):57－62．

［12］ Aptoula E，Lefevre S．A comparative study on multivariate mathematical morphology［J］．Pattern Recognition，2007，40(11):2914－2929．

［13］陈平，李庆民．基于数学形态学的数字滤波器设计与分析［J］．中国电机工程学报，2005，25(11):60－65．

［14］赵昭，刘利林，张承学，等．形态学滤波器结构元素选取原则研究与分析［J］．电力系统保护与控制，2009，37(14):21－25，35．

The Detection of Power Quality Disturbance Based on Morphology Filtering and Dynamics

Zhang Yi，Liu Guiying，Jia Xuerui，Lu Chao
(College of Electrical and Information Engineering，Changsha University of Science ＆ Technology，Changsha 410004，China)

For the detection and location of power quality disturbance signal，a dual structure of mathematical morphology filter combined with dynamic(Dyn)algorithm was constructed based on a detailed analysis of the Dynfeatures and the sensitivity of dynamics to noise，construct a dual structure of mathematical morphology filter combined of Dynalgorithm．The disturbance waveform in the grid was first pretreated to filter out random noise．Then，for the denoised signal waveform，the Dynalgorithm was applied to identify the signal’s distertion point through the extreme point of the signal and detect the starting and ending time of the disturbance．The Matlab simulation results showed that the proposed detection method boosted the advantages of simple calculation，fast operation，and accurate detection．

morphology filtering;Dynamics;disturbance detection;power quality

TM714

A

10.3969/j.issn.1672-0792.2015.06.003

2015－03－19。

张意 (1990-)，男，硕士研究生，研究方向为电能质量分析与控制，E-mail:330238255@qq.com。