复杂船舶围壁的传热多项式传递函数辨识

李伟光，杨海燕，李丽，李安邦，徐新华

1 中国舰船研究设计中心，湖北武汉430064

2 华中科技大学环境科学与工程学院，湖北武汉430074

0 引 言

船舶空调系统耗能占船舶用能的很大比例，降低其能耗对整个船舶行业的节能减排具有重要意义。空调负荷计算是空调系统设计的基础，是选择空调设备容量的依据。目前，船舶的空调负荷计算采用稳态算法，但得到的空调负荷与舱室实际负荷相差很大。实际上，由于船舶的流动性，随着舱外温度、海水温度、船舶行进速度及太阳辐射条件的变化，舱室内的空调负荷也随之变化。同时，船舶围壁本身存在蓄热性，外界热扰通过围壁传入舱室会有时间上的延迟和幅值的衰减。因此，分析船舶围壁的动态传热对船舶空调负荷准确计算和船舶节能具有重要意义。国内外关于船舶围壁传热的研究很少，大多采用稳态计算，传热系数则直接根据相关标准［1］和手册［2］提供的参考值或者简化算法来获取。

目前，在建筑空调负荷计算和能耗分析中采用的动态传热计算方法为反应系数法［3］和z 传递函数法［4］。通常采用直接求根法在频域内求解热传导偏微分方程和傅立叶方程获得反应系数和z传递系数，这种方法存在求根困难、失根等缺点。状态空间法［5］、时域法［6］也可求取反应系数和z 传递系数，但需要长时间的迭代过程。陈友明等［7］提出了一种计算围护结构动态传热的方法——频域回归法。该方法基于系统辨识理论，推导计算出围护结构动态传热的理论频域热特性，再用辨识算法从得到的理论频域热特性中获得围护结构的一些简单又等价的数学模型，即s-多项式传递函数，进而计算围护结构传热的反应系数与z传递函数。在已知室内、外边界的条件下，由围护结构传热的反应系数或z 传递函数可以计算围护结构壁面的瞬时热流。获取船舶围壁的传热传递函数是采用反应系数法或者z 传递函数法计算船舶动态传热的前提，对于船舶围壁等不规则结构，其传热传递函数很难通过理论推导得出。

根据系统辨识理论，在系统频域特征已知的情况下，可以通过参数辨识的方法获取系统的传递函数。频域有限差分（FDFD）法可以直接、快速地计算线性热力系统的频域热特性［8］。本文拟通过建立复杂船舶围壁的频域有限差分模型来获取该结构的理论频域热特性，然后采用参数辨识方法，对构造的复杂船舶围壁s-多项式传热传递函数的参数进行辨识。s-多项式传递函数计算得到的频域热特性与FDFD 模型计算得到的频域热特性的比较结果说明了辨识的s-多项式传递函数能很好地反映船舶围壁的动态热特性。

1 船舶围壁物理模型

船舶围壁结构较为复杂，文献［1］列出了不同隔热材料、尺寸的船舶围壁隔热结构形式。隔热结构可分为有金属骨架的和无金属骨架的绝热结构，绝热结构由绝热材料、面板和木衬条组成。本文选取其中典型的一种有空气层的隔热结构［9］进行分析研究。该种船舶围壁结构组成及尺寸（单位：mm）如图1 所示，各部分材料的物理特性参数如表1 所示。船舶围壁内部空气层不考虑对流作用，认为是纯导热，空气层的导热系数取为当量导热系数［2］，围壁内、外表面换热系数分别取为8 W/（m2·K）和80 W/（m2·K）［1］。

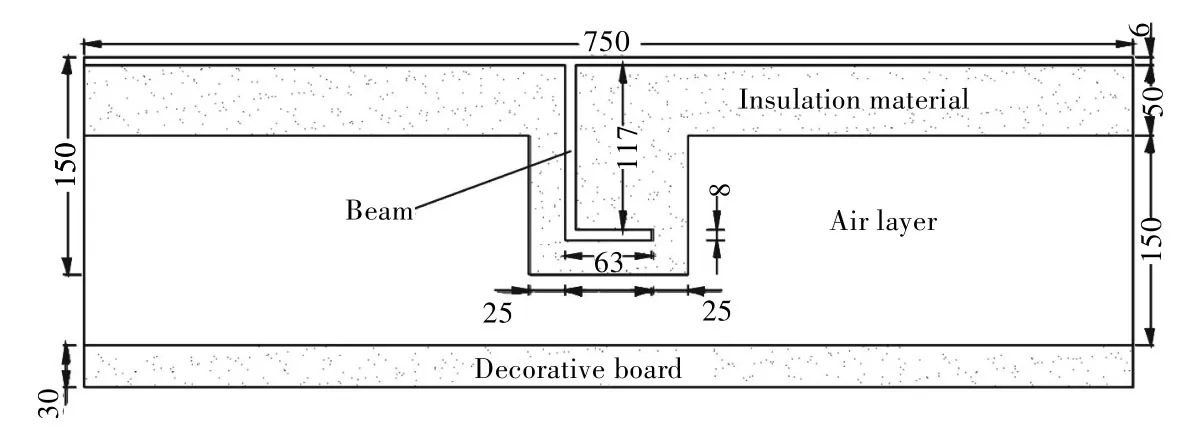
图1 船舶围壁结构Fig.1 Structure of ship casing wall

表1 结构各部分的物理特性参数Tab.1 Physical parameters of ship casing wall material

2 传递函数法

2.1 船舶围壁传递函数的基本描述

系统的s-多项式传递函数G(s) 表征了系统的特性，定义为：初始条件为零时，系统输出的拉普拉斯变换与输入的拉普拉斯变换之比。当已知热扰T(s)时，由围壁的s 传递函数G(s)，就可以得到围壁的输出响应，即Q(s)=G(s)T(s)。船舶围壁材料的物理特性参数可以认为是定常的，因此船舶围壁系统是线性定常系统，具有叠加性。船舶围壁传热的输入、输出响应可以用传递矩阵（1）表示：

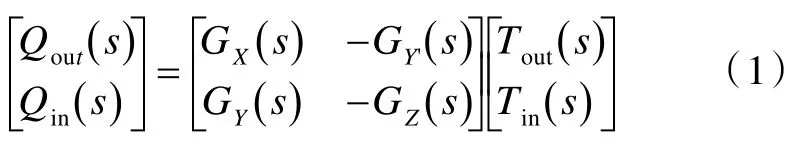
式中：GX(s)，GZ(s)为围壁内表面和外表面吸热s-多项式传递函数；GY(s)，GY'(s)分别为围壁由外到内和由内到外的横向传热s-多项式传递函数；Tout(s)为舱外空气综合温度；Tin(s)为舱内空气温度；Qout(s)为围壁外表面热流；Qin(s)为围壁内表面热流。对于平板型围护结构，G(s)可以通过对其传热微分方程作拉氏变换推导得出。但是船舶围壁结构不规则，其传热传递函数无法通过理论推导得出。由于船舶围壁是线性定常系统，可以认为其传热传递函数具有多项式传递函数的形式，即

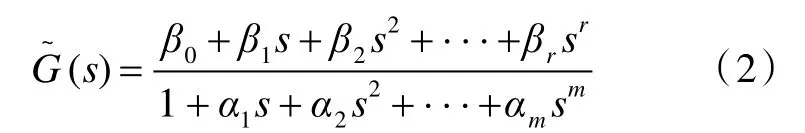
本文将通过建立船舶围壁的FDFD 模型来计算该结构的频域热特性，并采用参数辨识的方法来辨识复杂船舶围壁s-多项式传递函数的系数。

2.2 频域有限差分模型

FDFD 模型的基本原理是：采用经典有限差分法将二维模型离散成一系列的单元格，每个单元格由4 个热阻和1 个热容组成，如图2 所示；然后建立各单元的传热方程并进行频域求解，最终得到模型的频域热流响应。热容节点的温度可以表示成振幅为、频率为ω、初相位为Φ 的复指数形式，如式（3）所示。每个单元格与相邻4 个单元格的能量平衡方程如式（4）所示。将式（3）的表达式代入式（4），可以得到式（5）的热流平衡方程。最后，联立每个节点的热流平衡方程得到船舶围壁整个计算区域内的热流平衡方程组。

图2 船舶围壁的离散模型Fig.2 Discrete model of ship casing wall

给定不同频率的边界谐波热扰，对船舶围壁整个计算域内的热流平衡方程组进行求解，可以得出各个节点的u 和v，即获得了船舶围壁的频域热特性。从而进一步由式（1）可以得到船舶围壁的内表面吸热理论频域热特性GX(jω)、外表面吸热理论频域热特性GY(jω)以及横向传热理论频域热特性GZ(jω)。

2.3 s-多项式传递函数参数辨识

本文对船舶围壁的s-多项式传递函数的辨识实质是求得合适的s-多项式传递函数的系数，以使其频域热特性与理论频域热特性（由FDFD 模型计算得到）相一致。船舶围壁的多项式传递函数如式（2）所示，将s=jω 代入其中，就可以得到该多项式函数的频域热特性。船舶围壁传递函数的辨识过程可以描述为一个最优化问题：求得系数β0，β1，β2，…，βr和α1，α2，…，αm使得在给定频域范围内的目标函数（9）最小。本文采用最小二乘法求解此优化问题，所选取的频域范围为10-8～10-3rad/s，具体的求解过程可参考文献［7］。

式中：ωk表示第k 个频率点；IM(·)表示取复数的虚部；RE(·)表示取复数的实部；N 表示所选取频率点的总数。

3 计算结果分析

根据FDFD 模型计算得到10-8～10-3rad/s 频域范围内船舶围壁的频域热特性，进而通过参数辨识得到等价的s-多项式传递函数，如式（10）～式（12）所示。

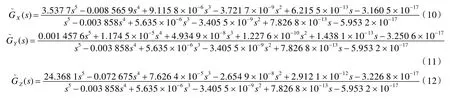
将s=jω 代入式（10）～式（12）便可得到s-多项式传递函数的频域热特性，即FDFD 模型可以计算得到船舶围壁的理论频域热特性，即GX(jω)，GY(jω)，GZ(jω)。s-多项式传递函数的频域热特性与FDFD 模型的理论频域热特性的比较如图3～图5 所示。

由图可见，两者的频域热特性曲线非常吻合，变化趋势一致。在低频区域，船舶围壁内表面吸热频域热特性与横向传热频域热特性的幅值基本不变，相位角接近于0。在高频区域，频域热特性的幅值和相位角随频率的变化较大，船舶围壁内表面吸热频域热特性的幅值是随频率的增加而增加，横向传热频域热特性的幅值是随频率的增加而减小，内表面吸热和横向传热频域热特性的相位角随频率增加而减小。在频率为10-5rad/s（周期为174 h，即7 d）时，船舶围壁内表面吸热频域热特性与横向传热频域热特性的幅值和相位角开始出现较大变化，船舶围壁传热呈现出明显的动态特征。结果说明，由参数辨识方法得到的s-多项式传递函数可以很好地反映船舶围壁（FDFD 模型）的动态热特性。图3～图5 的频域热特性也进一步说明了在实际周围环境的周期变化下，围壁的动态特性很强，在进行传热计算时需要考虑其动态特性。

图3 船舶围壁内表面吸热频域热特性曲线Fig.3 Frequency responses of internal heat conduction of ship casing wall

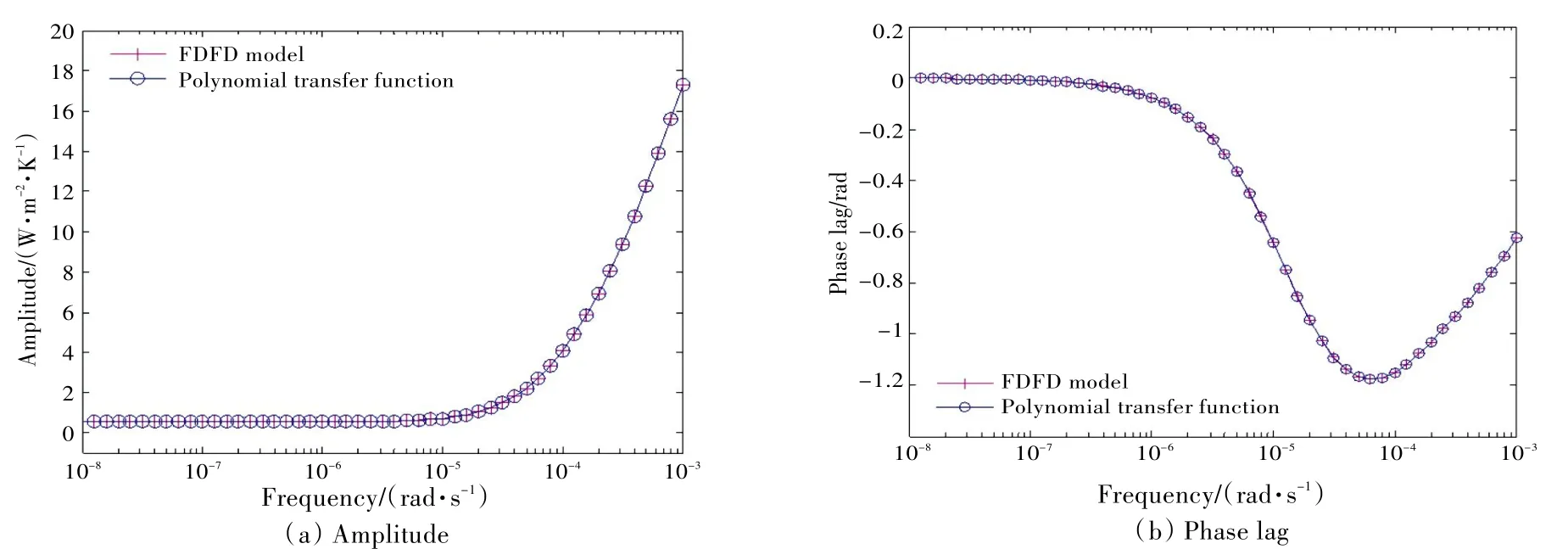
图4 船舶围壁外表面吸热频域热特性曲线Fig.4 Frequency responses of external heat conduction of ship casing wall

图5 船舶围壁横向传热频域热特性曲线Fig.5 Frequency responses of cross heat conduction of ship casing walls

4 结 语

本文构造了复杂船舶围壁的多项式传热传递函数，以该围壁的FDFD 模型计算的理论频域热特性为参考，采用参数辨识算法辨识了多项式传递函数的系数。s-多项式传递函数的频域热特性曲线与FDFD 模型的理论频域热特性曲线能很好地吻合，在低频区域，船舶围壁内表面吸热频域热特性与横向传热频域热特性的幅值和相位角基本不变，在高频区域（周期约小于7 d），频域热特性的幅值和相位角随频率的变化较大，船舶围壁传热呈现明显的动态特征。结果表明，通过参数辨识得到的多项式传递函数可以很好地反映船舶围壁的动态热特性，也进一步说明了在实际周围环境的周期变化下围壁的动态特性很强，在进行传热计算时需要考虑其动态特性。

［1］中国船舶工业总公司.GB/T 13409-92 船舶起居处所空气调节与通风设计参数和计算方法［S］. 北京：国家技术监督局，1992.

［2］陆耀庆. 实用供热空调设计手册［M］. 2 版. 北京：中国建筑工业出版社，2008.

［3］STEPHENSON D G，MITALAS G P. Cooling load cal⁃culation by thermal response factors method［J］.Ameri⁃can Society of Heating，Refrigerating，and Air-condi⁃tioning Engineers Transactions，1967，73（1）：1-10.

［4］CHEN Y M，WANG S W. Frequency-domain regres⁃sion method for estimating CTF models of building mul⁃tilayer constructions［J］. Applied Mathematical Model⁃ling，2001，25（7）：579-592.

［5］OUYANG K，HAGHIGHAT F. A procedure for calcu⁃lating thermal response factors of multilayer walls state-space method［J］. Building and Environment，1991，26（2）：173-177.

［6］DAVIES M G. Solutions to Fourier's equation and un⁃steady heat flux through structures［J］. Building and Environment，1995，30（3）：309-321.

［7］陈友明，王盛卫.建筑围护结构非稳定传热分析新方法［M］.北京：科学出版社，2004.

［8］朱求源，徐新华. 内嵌管式围护结构的频域热特性［J］. 华中科技大学学报（自然科学版），2013，41（11）：64-67.ZHU Qiuyuan，XU Xinhua. Thermal performance of ac⁃tive pipe-embedded building envelopes in frequency domains［J］. Journal of Huazhong University of Science and Technology（Natural Science Edition），2013，41（11）：64-67.

［9］李伟光，李安邦，徐新华，等.复杂船舶围壁传热系数取值探讨［J］.中国舰船研究，2014，9（2）：78-83.LI Weiguang，LI Anbang，XU Xinhua，et al. Heat transfer coefficient of complex ship casing walls［J］.Chinese Journal of Ship Research，2014，9（2）：78-83.