基于复合因子的空间划分耦合模型

陈玉鑫，游裔芳，江海东，陈天伟

（1.广西壮族自治区地理国情监测院，广西 南宁530023；2.中南大学 地球科学与信息物理学院有色金属成矿预测教育部重点实验室 ，湖南 长沙 410083；3.桂林理工大学 测绘地理信息学院，广西 桂林541004）

基于复合因子的空间划分耦合模型

陈玉鑫1，游裔芳1，江海东2，陈天伟3

（1.广西壮族自治区地理国情监测院，广西 南宁530023；2.中南大学 地球科学与信息物理学院有色金属成矿预测教育部重点实验室 ，湖南 长沙 410083；3.桂林理工大学 测绘地理信息学院，广西 桂林541004）

地形因子和数据密度是空间划分最重要的依据，利用微积分原理推导两者在微元定义下的函数关系，通过等价替代方程进行系统消参，减小系统误差，并结合正三角形空间划分和迭代思想推导其耦合模型，通过有限区域的变比例划分实现空间优化的目标，解决了非凸集合产生非法多边形的问题，最后通过算例验证和对比分析其优越性。

坡度；数据密度；空间划分；耦合模型；非凸集合

格网划分是GIS数字化关键技术之一，也是Grid DEM的空间数据模型。空间划分的性质与图像重构和空间统计密切相关[1]。Ahuja和Samet[2,3]认为规则空间划分至少应具有2种性质：①无限重复模式，并适用任何尺度图像；②可分解为无限精细的模式，并可表达成不同等级和层次的任意分辨率的空间要素。这2种性质要求把空间无约束划分为同形状的单元。Grunbaum和Shephard[4]证明规则空间仅有81种等面划分，但顶点类型相同的约束只存在11种划分，称为Laves划分，而把由正三角形、正方形和六边形组成的3种规则划分标识为[63]、[44]、[36]。Bell等[5,6]进一步提出空间划分的其他性质——均匀邻接和均匀划分。这些性质在图像处理和自动制图中有非常重要的作用。但是11种Laves划分中，仅[63]、[44]是无约束的规则空间划分，且只有[44]、[36]符合均匀邻接和均匀方向划分性质。

格网单元类型与间距是Grid DEM的基本属性[7]，Hutchinson提出了基于坡度中误差确定DEM最佳格网间距的思想[8]。汤国安强调“选择合适的单元大小，对实现空间分析很重要。格网单元过大DEM精度会降低，损失大量地形信息造成图形失真；单元过小就会产生大量数据的冗余和地形宏观特征的显示效果”[9]。因此地形起伏程度大的区域数据密度相对较高，地形平坦区域数据密度相对较低，从而减少数据冗余。

随着空间划分研究的进展，周成虎[10]阐述了地理格网模型研究进展，刘永和[11]和孙文斌[12]在非凸边界约束不规则三角网划分方面取得一定成就。这些划分方法严重忽视地形因子等约束条件，也忽视样本数据数量对建模稳健性的影响。

为了解决非凸数据集合产生非法边界以及非法格网问题，通过有限区域的变比例空间划分实现空间优化的目标，建立了基于地形因子和数据密度复合因子的耦合空间划分模型。

1 离散空间数据空间划分的约束条件

空间划分的性质制约格网类型选取，格网单元间距取决于空间划分的精度需求和数据密度。

1.1 单元类型的选取

由前面的公式推导过程不难看出，模型是建立在曲面函数连续可导条件下，模型推理中把不可直接度量的参数转化为用可直接度量的数据参数来表达，对于连续的地形模拟理论上是合理的，利用迭代思想的自相似原理也能很好地解决地形模拟数字化过程因为比例尺变换造成的不确定性问题。推导公式ρ = N* /（4N）反过来可以检验实际工程项目中测量数据分布的是否合理。

空间离散点边界样本点集合记为Bn（XN，YN，ZN），N∈n，n=1、2、3…。凸化多边形的外接圆直径为样本最远2点的距离， 圆心O平面坐标（OX，OY）为：

空间自动化划分的性质要求格网单元类型单一，而地学领域我们需要经常处理大量离散数据，离散数据分布的不均匀性使如何有效地进行空间自动化划分成为棘手问题。Voronoi图和Delaunay尽管是分析研究离散数据极其有利的工具，也是依据离散数据进行空间变比例表达地表形态的最佳方法，但其算法基础建立于半凸平面，面对复杂的地理不规则数据，划分会出现一些错误[13]。

云天化的产业链比较完整，在肥料板块，氮肥、磷复肥是云天化的传统强项，同时在产业上游还拥有宝贵的磷矿资源。段文瀚表示，在环保政策层层加码的今天，绿色发展已经成为行业的共识，云天化在这一方面始终走在前列。云天化所提倡的绿色科技，主要是指绿色矿山、绿色工厂、绿色产品。

尽管Voronoi图和Delaunay三角网能够很好地实现变比例空间划分，但是面对非凸集合，此时Voronoi图和Delaunay三角网算法就会出现非法边界及非法多边形，实验验证结果如图1～3所示。

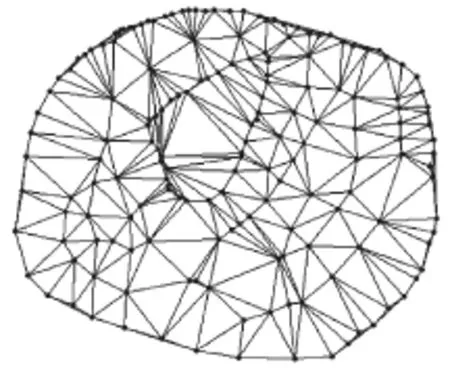
图1 非单连通边界约束Delaunay非法三角网图

图2 非凸边界约束Delaunay产生的非法边界

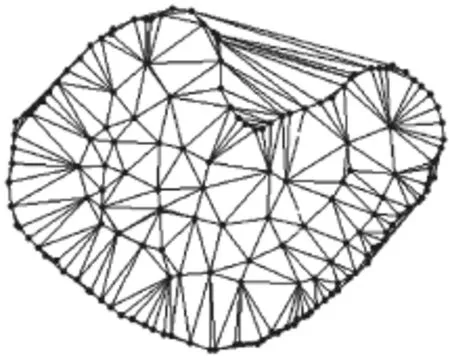
图3 非凸边界约束Delaunay非法三角网

考虑到地理对象空间的连续性和空间自相关性，又由于正三角形能4等分4个面积相等的小三角形来满足迭代的思想，初始化的正三角形与分割形成的4个小正三角形在数据结构上存在“父子”关系，“子”格网单元在数据结构上存在“继承”的特性，且在地学上用数学语言反映地理对象空间的连续性和空间自相关性。

2.1 坡度的微元定义

1.2 有限区域的变比例空间划分

坡度因子和数据密度都是在微元定义下用曲面方程Z=F（X，Y）来表达，如果直接求解曲面方程势必引入误差。如果坡度因子和数据密度都通过曲面方程函数等价替代来系统消参不仅可以减小误差，还可形成复合因子空间划分耦合数学模型。

有限区域的变比例空间划分的思想是把凸化的集合外接圆等分6等分，然后再对每个子区域进行空间划分，同时划分的数学模型是一致的。

1.3 边界约束条件

二维欧几里得空间，离散数据的边界常用凸包集合来表示，其算法研究归纳为：

1）增量式算法，其时间复杂度为O（n2）。

有文献报道[5],腹部CT能够清晰显示腹腔内肝脏、胆囊、脾脏、肾脏、胰腺等实质性器官结构的变化状况,故对于疑似腹部肿瘤、腹膜炎、腹部创伤者,且有超声检查结果作为支撑的,可进一步予以CT检查,以准确判断病灶的病变程度。

2）包裹法（Jarvis步进法），时间复杂度为O（kn）。

3）Graham扫描法，算法的整体时间复杂度是O （nlogn）。

2.1 两组营养指标变化情况 术后第4 d、第7 d ERAS组白蛋白值较传统组高，且差异具有统计学意义(P<0.05)。术后第4 d ERAS组前白蛋白值较传统组高，且差异具有统计学意义(P<0.05)。两组病人的血红蛋白值，差异无统计学意义(P>0.05)。具体见表2～表4。

4）分治法，时间复杂度是O（nlogn）。

随着我国人口老龄化与生活方式的变化，糖尿病从少见病变成一个流行病，对人们生活质量和寿命带来较大影响，成为不容忽视的公共卫生问题。有研究证明，依从治疗医嘱和生活管理是控制血糖的最好方法，若能将血糖保持在一个理想的水平，可有效降低糖尿病相关并发症的发生率。该研究在北京昌平区回龙观社区管辖的糖尿病患者中随机抽取100例，采用对照的方式，分析健康教育对糖尿病患者治疗依从性及疗效的影响。

（三）实现高端文艺演出“零”突破。投资1.2亿元建成天上黄水大剧院，造型美观，大气恢弘，充分突出了“天上黄水”歌舞主题，由国家级艺术团队倾力打造的一部土家大型歌舞。是一部以石柱山水文化为“点”，以土家儿女追求美好生活为“魂”，以唯美浪漫的现代高科技舞台为“景”的大型演出，极具民族性、艺术性、震撼力的土家大型歌舞。

5）快包法（Akl-Toussaint启发式），时间复杂度O（nlogn）。

显然，这些算法用来表达非凸集合离散数据的边界会产生非法边界及非法多边形。而要空间自动化划分，边界是不可逾越的约束条件。

单连通是凸集的充要条件，而非凸集合存在鞍部和非单连通两种情况。解决非凸离散数据集合产生非法边界和非法划分问题，有效方法是对非凸离散数据集合进行凸化，然后进行有限区域变比例空间划分。

边界约束首先进行样本数据的质心确定，然后求解凸化多边形的外接圆直径，最后求解每个子区间形成的最大正三角形的边界长度LK-max（K=1,2,3,4,5,6）。工程中采样点分为规则格网采样点和离散采样点。

综上所述，在航标巡检工作中，由于工作量相对较大，且受到海水情况、气候条件的影响相对较大，所以对其过程进行安全管理有着十分重要的意义。通过加大对于事故的追查力度、积极使用先进技术完成航标巡检、定期航标巡检的安全管理、特殊时期航标巡检的安全管理、组织进行专业的培训，在提升航标巡检的质量以及工作效率的同时，也对其过程的安全性进行了提高。

按照“平战一体、专司主营”的原则，各级装备保障部门要加快理顺领导指挥关系。平时，军以上装备保障部门应以核心骨干力量为主，领导组织部队的装备采购、管理、维护以及供应等工作；军以下联勤保障部门要主动适应新体制架构，实现联勤保障部门内部各级与相同职能的军以上装备部门的业务衔接。战时，军以上装备部门应以装备保障指挥机关的角色纳入一体化联合指挥部，指挥协调装备保障行动；军以下联勤保障部门应根据战区联指的指令，迅速进入战时装备保障指挥模式。各级装备保障机构平时应按照“常态运行、精干高效”的原则要求，简化装备保障组织实施流程，以便战时能够快速释放装备保障效能。

1.4 格网单元的二义性

格网单元的属性值取值方法有2种：①格网顶点均值，②格网内点的属性值。因本文是基于数据密度的建模，故用第2种，那么格网划分的二义性约束条件便是格网单元内只能有唯一点。分级格网内任意2点间的距离为Dp，格网单元的边长l,那么这个约束条件转化为数学表述为：

2 坡度与数据密度复合因子的空间划分数学模型

由于地形模型建模或者数字化过程中要素存在确定性和不确定性[14]，尤其在分级格网中尤为突出。研究区域范围内格网的级别不同，考虑到比例尺因素，那么数字化后会使原来的地形图出现局部失真和地形特征线信息损失等情况，对边界和地形起伏较大的区域影响尤甚。建立在自相似性原理基础上的地形、地貌特征的数字化模拟具有形状、功能、结构和信息等方面的相似性,或者统计指标上的一致性。

空间离散数据点（X，Y，Z），X为经度（或横坐标），Y为纬度（或纵坐标），Z为高程。地形在地理空间上存在连续性，地形因子的复杂程度对格网的划分大小产生重要影响，从而影响Grid DEM地形表述的精度。

地形因子的约束条件可用坡度来表达。地形因子坡度定义为经过该点的切水平面与水平面的夹角，数值上等于该点地表微分单元的法矢量n 与高程轴Z轴的夹角。设曲面方程Z=F（X，Y），其数学表达式为：

式中，fx为已知点X轴方向的高程变化率；fy为该点Y轴方向的高程变化率。

2.2 样本数据密度的微元定义

2.4 模型适用范围

式中，ρ为分级格网中数据密度；N*为分级格网中离散数据量；S为投影到该级格网的曲面面积；E为离散数据点微分单元的面积，其地学意义表示空间离散数据空间自相关性的度量。利用高等数学求曲面面积的计算方法，地形曲面Z=F（X，Y）有：

2.3 复合因子格网划分数学模型的建立

通常按照统一的网格数据标准填充到网格里,无法满足精度要求。表述地形地貌的离散空间数据具有离散性，数据属性不能表达空间实体对象的空间连续性，也无法反映空间自相关性。而离散空间数据组织结构却隐含这些关系，因此需要建立空间离散数据组织结构与地理实体间的数学映射关系来定量地反映地理实体间元素之间的本质关系。

平面格网即为曲面的投影，则有：

数据密度因子用曲面方程进一步表达为：

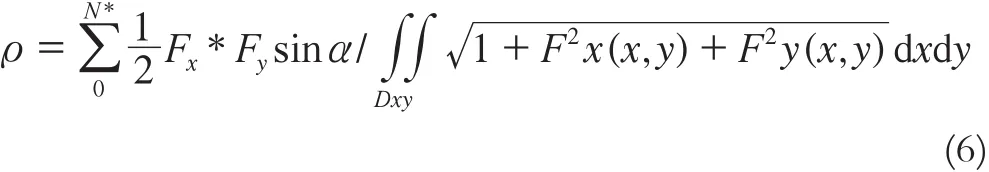
分级格网面积Sf可以间接求得，格网迭代次数设为N，格网单元面积设为e，则有：

化简取整为：

格网单元面积e为曲面面积微分单元E的投影面积：

投影下数据密度可推导出ρ = N*E / Sf，化简可得：

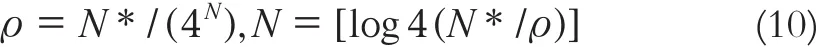
那么迭代思想下基于坡度和数据密度的复合因子模型为：

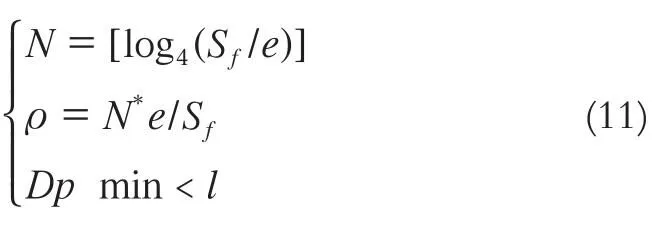
模型中格网单元边长Dpmin与e存在关系为：代回模型形成迭代终止条件。

目前，应用型民办本科高校是培养“双师型”教师队伍的主要途径，这些高校自发组织教师参加各种实践培训。虽然很多教师都提高了专业技能，但也同样会给应用型民办本科高校带来经济负担。由于缺少“双师型”教师队伍建设资金，从而导致教师培养规划失去连贯性，这不利于应用型民办本科高校“双师型”教师队伍的建设。

WANG Jiu-sheng, HU Fang-yuan, CAO Peng, ZHANG Xiao-ping, WEI Li, MEI Chang-lin

All authors declared that there are no con flicts of interest.

空间离散数据密度也是影响格网划分最重要的指标之一。设曲面方程Z=F（X，Y），则每个分级格网数据密度数学表达式为：

我看见她炒菜时，因动作太生猛，洒了一些油在燃气灶上，于是连声咒骂，因为注意力分散，接着又被油锅里溅出的热油烫着了。

本次研究干预之后，实施X线诊断，多层CT诊断及MRI诊断的检出几率存在一定程度上的差异，（P＜0.05）。详细见下表。

齐眉说，半个小时前我又联系了一次，“焦点调查”网站的吴限站长手机关机，其他几家负责人不是在出差，就是有别的事走不开。

3 模型的算例分析及对比验证

3.1 算法评价

时间复杂性T（n）和空间复杂性S（n）是衡量算法优劣的标准。Delaunay三角网是Voronoi图伴生图形，Voronoi图的算法复杂度[13]最优为：T（n）=O（nlogn）。本文数学模型是建立在迭代的基础上，利用显式方程求解，能够快速增加格网划分数量的同时计算机内存需求量较小和计算时间也较短，其算法时间复杂性为：T（n）=O（log4n），表明该模型具有快速收敛的性质。

3.2 算例分析与对比验证

本文以2010年广西桂林市灌阳县老人山RTK测量 数 据 为 例，Xmin=2 816 887．596，Ymin=516 821．934，Xmax=2 817 291．411，Ymax=517 276．207，在VB6．0平台下进行空间划分。由于VB计时器控件的时间间隔准确度不会超过l/18 s，所以采用API函数，依据《CJJ_100-2004_城市基础地理信息系统技术规范》，运行结果如图4。

Delaunay三角网运行的结果如图5所示。

图4 100x100正方形空间划分图

图5 试验数据生成的Delaunay三角网图

表1 程序耗时统计表

已知参数代入式（11）：试验数据110组，即N*=110，试验数据转化为WGS84坐标系下数据， 凸化外接圆直径R=区域最远两点距离,通过求解每个扇形区域的边界边长LK-max和每个区域最小两点间距l作为约束条件求解最小迭代次数：N=[log2（LK-max/l）]。可视化测试环境采用火狐浏览器及程序语言 Javascript，运行时间只有4 305 ms，可视化效果如图6所示。

图6 耦合空间划分模型运行可视化图

4 结 语

构建Grid DEM过程中，格网的划分是首要环节，格网划分方法造成的误差逐级传递，从而影响DEM质量、精度和空间分析。通过建立数据密度-坡度耦合模型，实现了以下目标：

1）利用等价替代方程系统消参，不仅降低建模难度，更减小误差的程度。

2）利用迭代算法满足空间自动划分的性质要求，模型计算方法可视化运行时间只有4 305 ms，是其他算法运行时间的1/4～1/3，验证了其快速收敛性质。

3）利用有限区域变比例划分，划分依据边界的空间位置、区域最小距离和区域最大距离等约束条件，解决了非凸离散数据集合产生非法多边形的问题。

4）利用地形因子和数据密度微元定义下的耦合，实现双因子约束条件下减小数据冗余的目标。

[1] 唐中实，黄俊峰，尹平，等．地理信息系统——原理与技术[M]．北京:电子工业出版社，2004

[2] Ahuja N ． On Approaches to Polygonal Decomposition for Hierarchical Image Representation[J]．Computer Vision，Graphics，and Image processing ,1983(24):200-214

[3] Samet H ．The Design and Analysis Spatial Data Structures[M]．Reading（USA）:Addison-Wesley,1989

[4] Grunbaum B,Shephard G C． The 81 Types of Isohedral Tiling in the Plane[J]．Mathematical Proceedings of the Cambridge Philosophical Society ．1977(82):177-196

[5] Bell S B M,Diaz B M, Horlroy F C． The Hor Quadtree:an Optimal Structure Based on a Non-Sqare 4-Shape[A]．// Mathematics in Remote Sensing[M]．Oxford,Press．1989

[6] Bell S B M, Horlroy F C． Tesseral Amalgamators and Hierarchical Tessellations[J]．Image and Vison Computing,1991(9):313-28

[7] 朱伟．1∶50 000 DEM最佳格网间距的确定[D]．长沙:中南大学，2009

[8] Hutchinson M F, Gallant J C． Digital Elevation Models and Representation of TerrainshaPe[A]．Terrain Analysis:Principles and Appieations[C]．New York:John Wiley&Sons．Inc,2000

[9] 汤国安，杨昕． ArcGIS地理信息系统空间分析实验教程[M]．北京:科学出版社，2006

[10] 周成虎，欧阳，马廷．地理格网模型研究进展[J]．地理科学进展，2009,28(5):657-662

[11] 刘永和，王润怀，齐永安．一种非凸包边界约束不规则三角网生成算法[J]．测绘科学，2008,33(3):79-81

[12] 孙文彬，刘希亮，栾晓慧，等．顾及等高线和凹边界特征的不规则三角网生成方法[J]． 地理与地理信息科学，2010，26(4):50-53

[13] 张宏，温永宁，刘爱利，等．地理信息系统算法基础[M]．北京:科学出版社，2006

[14] 承继成,金江军． 地形图的确定性与不确定性[J]．测绘科学,2007,32(1):7-8

P208

B

1672-4623（2015）02-0094-04

10.3969/j.issn.1672-4623.2015.02.035

陈玉鑫，硕士，研究方向为地理信息系统理论与应用。

2014-04-08。

项目来源：国家自然科学基金面上资助项目（41161072）。