基于特征线的点云数据分割算法

张大鹏，郑德华，夏佳毅

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

基于特征线的点云数据分割算法

张大鹏1，郑德华1，夏佳毅1

（1.河海大学 地球科学与工程学院，江苏 南京 210098）

为了提高点云数据分割的效率和精确度，基于深度图像和CANNY算子，研究了一种新的按照特征线的点云数据分割算法。结果表明，这种基于特征线的数据分割算法能够显著提高数据分割的精度。

特征线；分割；深度图像；CANNY算子

数据分割是点云数据处理中的一个重要环节，数据分割的好坏直接影响到曲面重构的质量[1]。国内外学者在点云分割方面已经作了大量研究。Jiang等[2]通过将扫描线分段拟合形成一组直线段来实现点云数据的平面分割，但效率较低；Besl和Jain提出区域生长方法识别数据中的同类区域[3]，仅局限于一个特定的模式；向日华和王润生提出的基于高斯混合模型的分割算法[4]，对于大量散乱点云的效果并不理想；Yokoya和Levine实现了一种基于边缘和基于区域生长的混合分割方式[5]，需要进行批量三角化，计算量大，难以精确识别特征点或特征线；丁益洪等人提出的基于随机Hough变换的分割算法[6]，仅考虑了单个点计算隶属度函数。

本文提出一种新的基于特征线的分割点云数据的方法。首先将三维点云数据转换为深度图像，利用CANNY算子来提取深度图像的边缘信息，然后将其转换到三维空间中。根据特征线上的点拟合出最佳平面，并计算特征线内点的邻域高度差，判断该点是否属于该平面，最后完成点云分割。

1 深度图像的生成

深度图像实际是带有距离信息的图像，它既包含空间三维信息，又具有视觉图像的特点。Besl在1988年提出了深度图像的表达形式：d（i，j）= f（xi,j，yi,j） (1)式中，d（i，j）表示深度信息，即扫描点到图像像面的距离S；（i，j）表示像素点的行列坐标。深度图像d （i， j）可看成二维矩阵，即有0≤i≤M-1，0≤j≤N-1；矩阵元素为图像像素，M×N表示图像的大小，即行数和列数。

二维矩阵与图像的像素点是一对一的映射关系。因此，可根据扫描点在栅格中的位置（行列号）定位其在图像中的像元的位置。根据扫描点到图像像面的距离S 确定该点对应像元的灰度值，即Z方向代表深度，如式（2）所示，距离和灰度值成正比关系：

式中， Smin和Smax分别表示点云数据到扫描仪中心的距离的最小值与最大值。

为了方便后续点云数据处理，需要创建另外一个图像数组，其像素为Pi=（xi，yi，zi），其中（xi，yi，zi）表示该点在三维直角坐标系下的坐标。这种形式的深度图像无法以灰度图像的形式直接显示出来，但由于扫描点的位置可以根据深度图像中的像元位置（即扫描点在栅格中的行列号）来确定，使得这种扫描点云拓扑结构的建立方式提高了后续数据处理的效率。

2 深度图像的边界探测

之前有很多的算法可以探测图像的边缘信息，如Kirsch、Prewitt、Laplacian等，但它们的鲁棒性较差，对噪声较敏感，无法高效率地提高图像的实际边缘。

本文采用Canny算子对深度图像进行特征提取。Canny算子满足3个判断准则：信噪比准则，定位精度准则，单边缘响应准则。Canny算法是高斯函数的一阶导数，是对信噪比与定位精度乘积的最优化逼近算子[7]。其分为4步，分别是图像平滑、边缘检测、阈值分割及边缘定位，具体如下：

1）采用高斯滤波器，对图像f（x，y）进行平滑滤波，高斯函数公式为：

2）用一阶偏导数的有限差分计算平滑后的图像梯度∇g（x，y）和方向θ（x，y）：

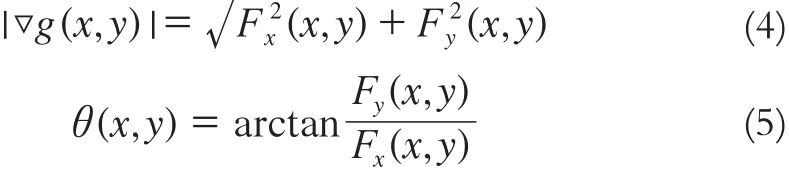
Fx（x，y）、Fy（x，y）由G（x，y）在x 方向和y方向的偏微分分别与图像卷积得到。

3）对梯度进行“非极大值抑制”， 为了细化幅值图像中的屋脊带，保留局部梯度极大值及在该点处梯度突变最大的像素点。

本文采用开放式的阈值设置方法，用户可以自己调节高低阈值及σ的大小，以得到最满意的边界数据。

3 生成初始特征线

根据得到的特征点及其在栅格中的索引，利用点之间的距离关系将相近的点连接起来。

具体步骤如下：

1）确定起始点。本文以索引顺序搜索，从特征点中第一个点S0开始，根据点云数据的分辨率定义距离阈值dmax。不同的三维点云数据的扫描间隔是不同的，根据不同的扫描间隔来定义距离阈值dmax(本文中实验所用点云的扫描间隔为10 mm，距离阈值dmax设置为15 mm)。

2）在S0的近邻中计算特征点集与S0的距离d，搜索距离最近的2个点P、Q。若其距离d

3）在S0的近邻中搜索距离最近的点Pi，若其距离d

4）在特征点集未访问的点中，取一点Pi赋值给S0，重复第2）、3）步，直到所有的点处理完毕。

若该终点的邻点中包含起始点S0，则该特征线封闭；若不包含起始点S0，则特征线不封闭。

4 提取平面点

每个三维点的特征向量表示它邻域的最主要特征。特征向量由3个属性组成其中hi是点i相对于其邻点的高度差，是点i的单位法向量，di是切平面到原点的距离。高度差hi是由点到其邻点的最佳拟合平面的距离。点与其邻点的高度hi通常用来测量曲面局部变化。hi值表示曲面的变化：值较小表示点位于曲面上，而值较大表明曲面波动较大。则此点的高度差h为：式中， （a，b,，c）表示平面的单位法向量， a2+ b2+c2= 1；d表示坐标原点到该平面的距离。根据hi的大小能判断不同的曲面类型。对于均匀的点密度和均匀程度的噪音的平面点云数据，若hi约等于0说明点在曲面区域内。然而，如果是曲面点云数据，点到最佳拟合平面的距离将大于0。利用高度差来识别点是否属于平面是很好的方法。

提取平面点的具体步骤如下：

1）将特征线按点云数目排序，从特征点数目最多的特征线开始计算。

2）在特征线上的点云中任选3点（P1，P2，P3），构造一个平面L，利用特征值法计算a、b、c的初始值。

3）根据计算出的a、b、c值，按照公式计算出该扫描线上其余点至平面L的距离di。统计di小于阈值2σ的点的个数，作为L的分数SL。

4）重复第2）、3）步Cn3/2次，选择出分数最高的平面L'，重新计算最佳的a、b、c值。

5）以平面L'为最佳拟合平面，运用式（6）计算特征线内的点的高度差h，设置阈值ε，判断h是否小于阈值ε，高度差小的即可认为是平面。

6）将平面点标记为已访问，计算下一条特征线，直到所有的点访问完毕。

其中，阈值2σ为距离di的标准偏差，其计算公式为：

5 实验分析

对RealWorks软件中提供的某培训数据进行处理，如图1所示，共有145 329个点。将其转换成深度图像，如图2所示，像素大小为512 416。

图1 原始点云数据

图2 深度图像

因为此扫描对象为平面，其特征边缘都为跳跃型，所以直接对深度图像采用边缘检测算子进行特征提取就能取得较好的结果，如图3所示。转换为点云如图4所示，共检测到2 854个特征点。将特征点连成特征线，共有特征线33条，其中闭合特征线7条，如图5所示。对其进行平面点的提取，结果如图6所示。利用提取出来的平面点进行平面拟合，其标准差为78.52 mm。若直接采用原始点云数据进行平面拟合，其标准差为120.33 mm。可见，对于平面点云数据，本文算法可有效快速地提取出点云数据的特征点，并提取出平面。

P237.3

B

1672-4623（2015）03-0120-02

10.3969/j.issn.1672-4623.2015.03.042

2014-03-17。