RSA算法的分析与改进

中南林业科技大学计算机与信息工程学院 陈鹏飞 何小东

RSA算法的分析与改进

中南林业科技大学计算机与信息工程学院 陈鹏飞 何小东

RSA算法是一种非对称的公钥加密算法，它广泛应用于数据的加密和数字签名和身份验证等领域。针对RSA算法中寻找安全大素数实现难度较大，运算时间较长，本文提出一种简洁的大素数产生的改进算法。该算法经实验测试，通过提高了RSA算法中大素数的生成效率，减少了RSA算法加解密时间，有效地提高了RSA算法的效率。

素数；RSA算法；加密与解密

1 引言

近些年,随着计算机的普及与计算机网络的快速发展和广泛应用,信息安全变得越来越重要。信息安全的基础是密码学。为了保证数据的安全,通常需要对数据加密,目前常用加密算法有:对称加密算法和非对称加密算法。对称加密算法体系(如DES算法、AES算法),非对称加密的算法体系(如RSA算法、Elgamal算法,ECC算法)。RSA算法是一种非对称的公钥加密算法,它是目前公认在理论和实际应用中最为成熟和完善的一种公钥密码体制。从目前应用的角度看,软件实现的RSA已经开始广泛的运用于计算机网络数据加密,密钥分配,数字签名与身份认证等领域[2]。

RSA算法的基础是数论的欧拉定理,其安全性依赖于大数的因数分解,即依赖于RSA算法中的512bit以上的安全大素数,但是安全大素数寻找相对困难且运算时间较长。目前,国内外针对RSA加密算法的研究也主要集中在效率和安全性两个方面。大素数的生成在RSA算法中很重要,为了确保RSA算法的安全性,只能使素数的位数增加,但素数的位数增加以后,为了避免降低算法的效率,就要求加快素数的生成效率[3]。本文针对RSA加密算法的特点,提出一种简洁的大素数产生的改进算法。通过提高了RSA算法中大素数的生成效率,以提高RSA算法的运行速度,并在Microsoft Visual Studio 2013中编写程序并测试与验证。

2 产生素数的算法

RSA算法是建立在“大数分解和素数检测”的理论基础上,素数的产生效率也决定了RSA算法的性能。RSA算法的安全性是基于大数分解的难度,其中生成的公钥与私钥是一对大素数的函数。从公开的密钥和密文中恢复出明文的难度,等同于分解两个大 素数的乘积[4]。素数(质数)是对于正整数p(p〉1),p的因子仅为1和p本身。RSA算法原理如下:

③随机选取一个数作加密密钥e(1〈e〈φ(n)),使e和φ(n)互为素数。

④利用欧几里德扩展算法计算e的逆元,即解密私钥d,以满足,则(n,e)为公钥, (n,d)为私钥,e为加密指数,d为解密指数。

图1 RSA算法加解密过程

在RSA算法中,关键就在于选取两个大素数p和q,它是后面步骤的基础。但是如何判别一个整数是素数一直是RSA算法中的难点。传统的素数生成方法是先随机选择一个或者多个较大的奇整数,然后来测试选取的大数是否为素数。一般方法如下∶

(1)随机生成一个大奇整数N(可以利用随机数产生器)。

(2)随机选择一个整数a(a〈N)。

(3)然后进行素性测试,如果N没有通过测试,则拒绝N,并转到步骤(1)。

(4)如果N通过测试足够多次,则接受N;否则转到步骤(2)。

其中,进行素性测试主要采用的是概率性检测方法(如Miller-Rabin素性测试),即判定一个数是素数比较难,但否定它是素数则要容易得多。Miller-Rabin算法描述如下:为了测试一个奇整数N是素数,对随机选择的整数a(1〈a〈N-1),重复调用Test(N),如果某个时刻Test返回“合数”,则N一定不是素数;如果Test连续t次返回“不确定”,当t足够大的时候,则可以说明N是素数。上述算法可以表示如下:Test(N)

(2)随机选择一个整数 a(1≤a≤N-1);

(4)如果h=1或h=N-1,则N通过测试,N可能是素数,测试结束;

(6)若h=1,则N不是素数;如果h=N-1,N可能是素数,测试结束;

在上述Miller-Rabin素性测试算法中,当N通过一次测试,则有25%的概率判定N不是素数,因此可以计算得出,如果N通过t次测试,N是素数的概率为(1-()),当t=5时,N是素数的概率已经有99.90%[5]。但是传统的素数产生方法比较复杂、耗时较长、不易理解,而且目前尚没有较好的方法来生成两个大素数p和q。因此,本文对RSA中素数的产生算法进行改进,提出一种简洁的大素数产生的改进算法。算法实现的步骤如下:

S1∶可设置生成大素数的位数nbite;

S2∶随机产生一个nbite位大整数Bignumber,并设置最高位和最低位都为1(最高位为1确保素数达到要求的位数,最低位为1确保它是奇数);

S3∶选取j(自定)个小素数,存储到数组Primes[i]中,每次偏移量为2;

S6∶如果y=0,表示无余数,表示该数不是素数,退出循环,否则,ii+1,转到S2。

S7∶如果y不为0,则返回输出这个大数;

S8∶然后进行5次Miller-Rabin素性测试,通过测试,输出这个素数,否则,转到S2。

在S2中随机产生一个nbite为大数,本文采用了随机递增法:算法描述如下:

(1)随机选取一个nbite位大数N;

(2)对N进行素性检测,如果满足条件则返回N,否则转到(3);

(3)N=N+b(b是一个常数),转到步骤(2)。

本文在Miller-Rabin素性测试中,首先分解N-1=(b为奇数)时,用b来替换指数(N-1)/2,来提高算法的效率。其实现的算法如下:

i=0,b=N-1;

While(b%2==0)

{ t=t+2;b/ =4;

if(b不为整数)

{ t--;b* =2;

}

}

3 改进后的素数产生算法的验证

(1)实验环境:采用的主要硬件环境为:CPU Intel(R)Core(TM)i3 M 380 @2.53GHz,内存为4GB,500G硬盘。操作系统∶window7旗舰版(x64)。

开发工具:Microsoft Visual Studio 2013。

用C++程序设计语言在Microsoft Visual Studio 2013中编写程序并测试。

(2)实验结果:实验中可设置生成大素数的位数32,64,128,256等(则可以产生相应位数的密钥)。本文测试了当大素数位数为32位和64位时,所产生的公钥与私钥,并对密钥进行了十六进制转化,结果分别如图2和图3所示。

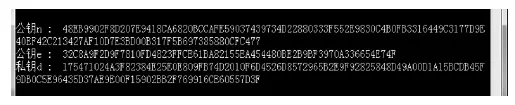
图2 素数为32位时生成的密钥

图3 素数为64位时生成的密钥

由图2和图3可见,本文改进后的算法可以产生不同位数大素数的情况下的相应密钥,证明该算法是可行的。

4 RSA算法测试结果与分析

在前述的实验环境中,本文对RSA算法进行了实验,对明文、密钥和密文都进行了16进制的转化,并测试了RSA算法加密与解密的时间。在实验中设置生成大素数的位数为32位和64位,输入明文为:“abcdefghijklmnopqr stuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ 0123456789”。实验结果分别如图4和图5所示。

图4 素数为32位RSA算法加解密时间的测试

图5 素数为64位RSA算法加解密时间的测试

从图4和图5两图可见,在明文大小相同的情况下,使用同一种算法,随着大素数位数的增加,密钥长度变长, RSA算法加解密时间也越长;也可以测试出,在密钥长度相同的情况下,随着明文长度的增加,加解密时间也相应的增加。可见,本文改进后的算法实现了密钥的产生和明文的加密与密文的解密,较好的实现了RSA算法。

RSA算法加密与解密时间分别是指对明文进行加密与对密文进行解密的时间。RSA算法的加解密速度一直是人们研究的重点。在前述实验环境中,采用上述的测试文本(明文)和1024位模数(大素数长度为512位),采用传统的素数产生算法和本文改进后的素数产生算法进行了5次测试,其结果见表1。

表1 测试结果

从表1可见,采用改进后的算法,缩短了RSA算法加解密时间,加解密效率进一步提高。本文通过提高RSA算法中大素数的生成效率,提高了整个RSA算法的加解密效率,可见,该算法是可行的。

5 结语

大素数的生成是构造RSA算法中密钥的关键,因此素数的生成和测试一直都是公钥密码学领域研究的一个重要课题。本文提出了一种改进的素数产生算法,实现了其密钥的生成。同时测试了不同位数的大素数情况下,相应RSA算法加密与解密所用的时间。最后,与传统的素数产生算法对比,通过提高了RSA算法中大素数的生成效率,使整个RSA算法的加解密时间进一步减少,效率进一步提高。

［1］谭浩强.C++程序设计(第2版)［M］.北京:清华大学出版社,2011.

［2］卢秀慧,杨瑞峰,贾建芳.RSA加密算法的快速实现［J］.沈阳建筑大学学报(自然科学版),2012,28(6):1143-1147.

［3］高雪寒.大数相除快速算法在RSA中的应用与研究［D］.西安:陕西师范大学,2014.

［4］汤鹏志,李彪.基于频率的大素数高效生成算法［J］.华东交通大学学报,2011,28(5):52-56.

［5］孙伟.公钥RSA加密算法的改进与实现［D］.合肥:安徽大学,2014.

陈鹏飞（1990—），男，四川南充人，中南林业科技大学硕士研究生，研究方向：密码学与网络信息安全。