Study on Maize-water Model for Supplemental Irrigation in Loess Plateau
2015-02-05XingLIMangmangGOU
Xing LI,Mangmang GOU
1.Inner Mongolia Engineering Research Center for Water-saving Agriculture,Inner Mongolia Normal University,Hohhot 010022, China
2.Institute of Water Conservancy Science,Inner Mongolia,Hohhot 010020,China
Study on Maize-water Model for Supplemental Irrigation in Loess Plateau
Xing LI1*,Mangmang GOU2
1.Inner Mongolia Engineering Research Center for Water-saving Agriculture,Inner Mongolia Normal University,Hohhot 010022, China
2.Institute of Water Conservancy Science,Inner Mongolia,Hohhot 010020,China
The Loess Plateau has a typical semi-arid climate,and the area suffers from very harsh ecological environment,severe soil erosion and water runoff,and uneven distributed precipitation.Due to the relatively low holding capacity,current rainwater-collecting and conservation facilities can only supplement a maximum of 18 mm of water for crop production in each irrigation.In this study,mathematical models were constructed to identify the water requirement critical period of maize crop by evaluating response of each individual developmental stage to supplemental irrigation with harvested rainwater.In the transformed Jensen model,ETmin/Eta was used as the index of relative evapotranspiration.The use of relative yield and relative crop evapotranspiration was able to eliminate influences from unintended environmental factors.A BP neural network crop-water model for extreme water deficit condition was constructed using the index of relative evapotranspiration as the input and the index of relative yield as the output after iterative training and adjustment of weight values.Comparison of measured maize yields to those predicted by the two models confirmed that the BP neural network crop-water model is more accurate than the transformed Jensen model in predicting the sensitivity index to waterdeficit at various growth stages and maize yield when provided with supplemental irrigation with harvested rainwater.
BP neural network;Model of crop response to water;The transformed Jensen model;Supplemental irrigation with harvested rainwater
A s water resources crisis worsens on the Loess Plateau in China,rain-fed agriculture has become a major activity in agricultural development in this arid and semi-arid region.Rainwater harvesting projects collect rainwater across multiple spatial and temporal scales,thus providing an effective approach to using natural precipitation[1-7].But due to small water storage capacity,current rain water collection facilities can only harvest a limited amount of water.The relationship between plants and water is very complex[8-10].Current models for water use as a function of crop production are constructed using the addition or multiplication mathematical principles[11-16].None of those models can accurately simulate the relationship between water and plants.For instance,when Jensen model was used to fit the experimental data under water deficit conditions,the resultant non-linear model predicted a negative sensitivity index at certain growth stages.To resolve this issue,Guo et al.proposed that the relationship between accumulation function of sensitivity index and the plant growth periods should fit to a sine curve[17-18].The logistic growth curve was also used to fit the accumulation function of sensitive index.Both models were able to produce reasonable results.However, the curve model for the accumulation function of sensitivity index is a nonphysical model and it is liable to cause some errors,although the scale of the errors and the subsequent impact on simulation accuracy is not yet known[19].Jensen model is the most commonly used simulation method in under-sufficient irrigation experiments where the well-irrigated treatments are used as the control samples[20-21].Various correction coefficients from a combination of different factors are also integrated into Jensen model[22],and the construction of a transformed Jensen model that can predict the crop-water relationship for the system of supplemental irrigation with harvested rainwater is critically important for the Loess Plateau region.
Based on the record at the Rainwater Harvest Experimental Station in Junggar,Qiandu town,Inner Magnolia,this area has very limited water resources.Under this circumstance,this study designed the experiment where supplementing rainwater at each of the maize growth stages was the treated whereas no-irrigation across the whole growth period was the control. The relationship between final yield and the water status at each growth stage was treated as a complex nonlinear approximation problem.A BP neural network maize-water model under extremely water deficit condition was constructed.This model was used to predict the optimal timing of supplemental irrigation with rainwater to produce the highest yield.This study has provided theoretically bases for developing a crop production system using harvested rain water resources to produce high yield and high water use efficiency in arid and semi-arid regions.
Materials and Methods
Field experiment
A field experiment was performed from 2003 to 2007 on a Water Collection and Supplemental Irrigation Experimental Station in northern Junggar,Ordos,Inner Mongolia.This typical semi-arid is on the Loess Plateau facing serious water erosion problem. Over 30%of the land is drenches and gullies connected with each other.Elevation ranges from 1030 m in the deepest gullies to 1 320 m at the top of mountains.The scarce rainfall is concentrated in a very short time period.
In the spring and fall,this area experiences large daily temperature fluctuation.The multiple-year average temperature is 7.2℃,the annual sunshine duration hours is 3 117.3 h,the accumulated temperature at above≥10℃is 3 500℃,the annual wind speed is 2.3 m/s,and the average non-frost season is 145 d.The multiple year average precipitation is 392.1 mm.Rainfall is distributed unevenly across spaces and time,it occurs mostly in summer and fall.Plants receive 60%of the life-time water from July to September.The multiple year evaporation is 2 093 mm,which is five times of total precipitation.
In the field experiment,each treatment group consisted of three replicate plots of 34 m2each,and 2 m wide barrier crop zone was set up between treatments.Maize cultivar‘Zhedan No.7’was sown at a rate of 37.5 kg/hm2and spacing of 30 cm x 50 cm.Crop density in the field was approximately 5.25×10 plants/hm.
Supplemental irrigation was applied using a ground level fixed plastic hose pressure-controlled drip irrigation system controlled through a water meter.Based on the amount of water in the reservoirs and the capacity of collecting rain water and the efficiency of the irrigation system,supplemental irrigation of 18 mm at each grow stage was scheduled.The experimental design in 2006 was described in Table 1.
The transformed Jensen model under extreme water deficit condition
A mathematical model of watercrop production function simulates the relationship between crop yield and periodic water consumption,and it also provides the basic knowledge for designing water saving irrigation and management plans.Jensen model is the most frequently used periodic water-production function model.In this model crop evapotranspiration is the variable to be used to predict effects of different water deficit levels at each growth stage on final crop yield.The equation for Jensen model is written as follows:
where n—the number of crop growth stages;
i—code of crop developmental stage;
λi—the sensitivity indexes at growth stage i;
ETai—the actual evapotranspiration at growth stage i (mm);
ETmi—the evapotranspiration potential at growth stage i corresponding to Ym(mm);
Ya—the actual yield(kg);
Ym—the highest yield potential under well-irrigated condition(kg).
In previous studies,sufficient irrigation was used as the control for the non-sufficient irrigation treatments, results from those experiment represent the effect of water deficit at each growth stage on final yield.Due to the natural environment and climate conditions in the Loess Plateau and the small amount of precipitation collected and would be available for supplemental irrigation,in this study non-irrigation across the whole growth period was used as the control for treatments of irrigation at each growth stage.Therefore,results from this study would represent sensitivity of yield to supplemental water at each growth stage.The equation of Jensen model was modified as follows:
where:ETmin—the amount of actual evapotranspiration corresponding to Ymin(mm);
Ymin—the lowest crop yield(kg); ETmin/ETa—index of relative evapotranspiration;
Ymin/Ya—index of relative yield.
BP neural network model
Artificial neural network(ANN) started in the 1940s,and it gained momentum in the 1980s.During the last 20 years,a second wave of interest in exploring this modeling system has formed.ANN is a powerful method that simulates human brain basic structure and function to solve non-linear high dimension and high-order data information questions.The data processing method is characterized by strong self-organizing,selfadaptable learning and memory association ability.Over 80%of ANN models use the BP reverse path forwarding transmission network modeling scheme.The BP modeling can process input and output identification of nonlinear dynamical systems,and the weight values are adjusted by using the back propagation learning algorithm for training the network[23].
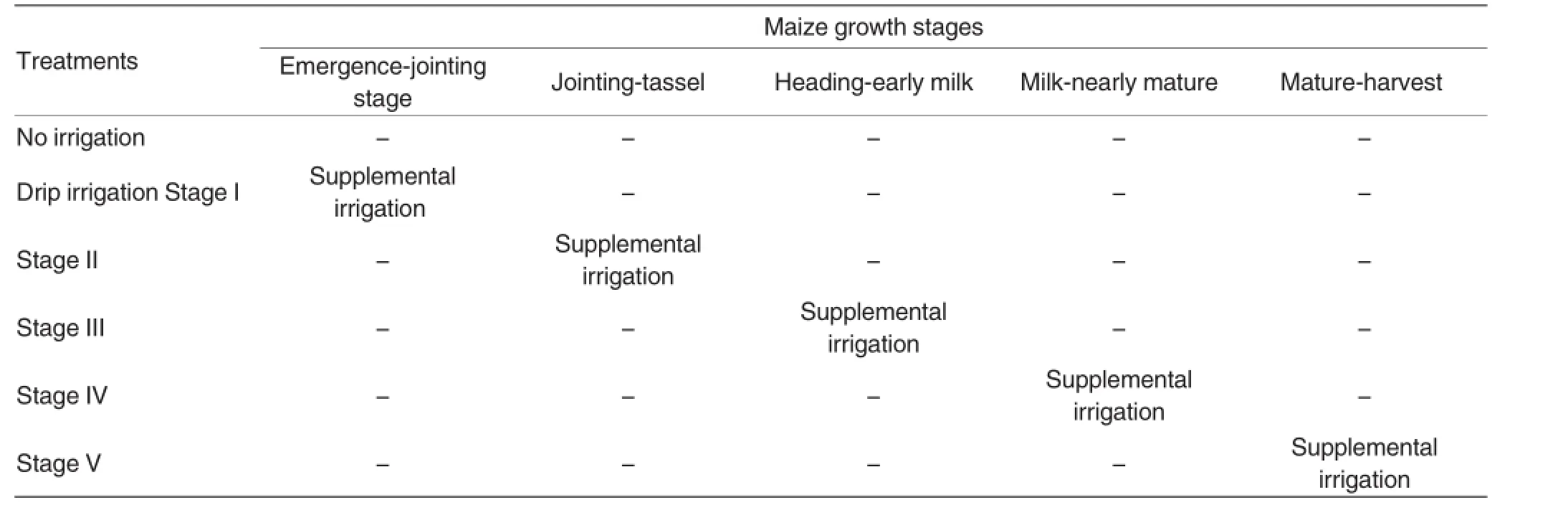
Table 1 The supplemental irrigation schedule of maize crop in 2006
Determination of the number of layers in the network model
BP network model has multiple layers which fit to the nonlinear differentiable function by performing weight training, therefore complex non-linear function approximation problems can be resolved using the BP network containing single hidden layer.In this study,a three layer network structure was used.
The activation function for each layer of the network in the BP model
The BP network’s capacity in nonlinear approximation is embedded in the sigmoid activation function, therefore hidden layers normally use such function.The sigmoid or linear transfer function can be used at the output layer.The sigmoid transfer function reaches a non-linear approximation faster,but the output is restricted in the range of 0-1 or-1-1.After comprehensive analysis,the tan-sigmoid transfer function was used at the hidden layers using the following program:f(x)=(1-e-2x)/(1+e-2x).The output layer transfer function was purelin [f(x)=x],which can take on any values.
Determination of the node number per layer in the BP network model
Selection of units in the hidden layers is the key for determining the node number per layer in the BP network. The accuracy of the model can be comprised if too few nodes are selected.But using more nodes in the network will increase the amount of training time.Normally the trial-and-error method is used to determine the optimum number of hidden nodes.Selection of input and output layer depends directly on the input and output variables for solving the real problem, therefore these parameters are easy to determine.In this study,according to physiological properties of maize crop,the whole growth cycle was divided into five stages:Emergence-jointing stage,Jointing-tassel,Heading-early milk,Milk-nearly mature,and Matureharvest.
In the model,the input layer had five 5 neurons each corresponding to the relative evapotranspiration at one of the five growth stages.One neuron was selected for maize yield at the output layer.The learning rate was derived by changing the training parameters for all the items,it was adjusted with the error-correction rule during the training process.The initial learning rate had very minimal effect on the network training output.After several iterations,the learning rate reached 0.05 when the fitting error was 0.0001 at eight nodes.The final network structure was 5-8-1.
Results and Analysis
Field experiment
The collected data include soil water content,the amount of supplemental irrigation,and precipitation. The evapotranspiration level at each growth stage was calculated using the following equation:
where
ETa—the measured evapotranspiration(mm);
Woand Wt—water content of soil in the top 1 cm layer at the begging and the end of each treatment period, respectively(mm);
Po—the effective precipitation during each growth stage(mm);
K—the amount of underground water fed to plants during each treatment period.In the study area,underground water level was below 50 m and no underground water was available to the crop,therefore K value was 0(mm);
M—the amount of irrigation for each time period(mm);
I—the amount of precipitation infiltrated into deep soil layers.Water content was measured to be 0,therefore I was 0(mm);
U,R—the amount of lateral water feed and seepage.The experimental site was located on the land,therefore the U and R value were both set at 0(mm).
Results from the 2006 field experiment and the dataset derived using equation(3)were presented in Table 2.
Training the BP neural network model
In the BP neural network cropwater model,the index of relative evapotranspiration was the input and the corresponding yield indices from different treatments at the same growth stage were the output values. This would have eliminated the unintended influences from climate factors. In the network training process if the weight values are set too big,with the increased weight gain from all the neurons the input of the activation functions would fall in the saturation region of the sigmoid transfer function,then it will lead to small derivative values thus disabling the adjustment procedure of the corresponding network weights. For input data value in the 0-1 range, a preventive strategy is to place the input data with bigger weight values inthe sigmoid activation function region with large gradient at the hidden layer.
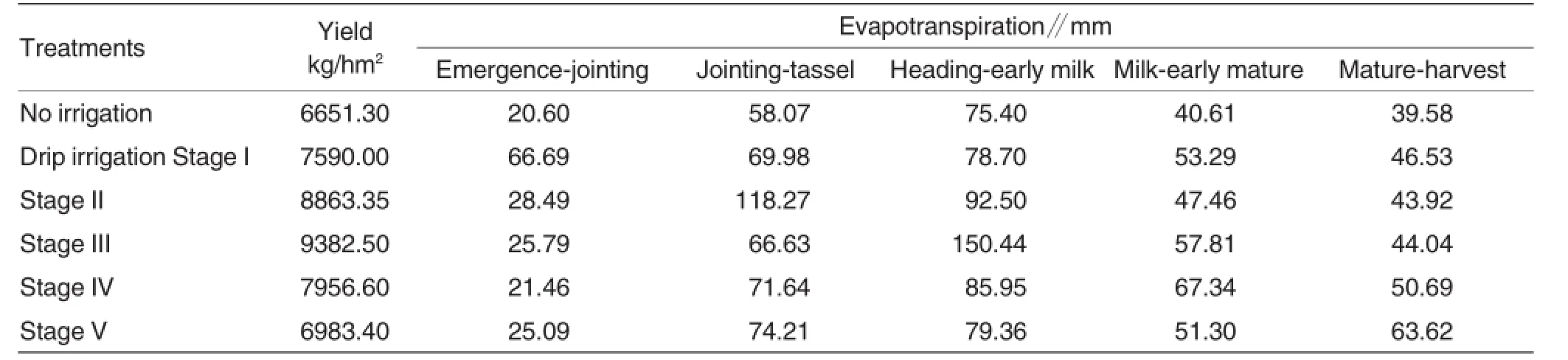
Table 2 Maize yield under supplemental irrigation of collected rainwater at different growth stages
The BP neural network training program was written using the MatLab language.Experimental data in Table 2 were converted to the indices of relative evapotranspiration and relative yield using the matrix computation.The link weight values of the layers after training are as follows:
The trained BP neural network model was then used to simulate maize yield from supplemental irrigation treatments(Table 3).The relative evapotranspiration index(ETmin/ETa)was used as the input to predict the relative yield index(Ymin/Ya) from each irrigation treatment,which was then used as the index of yield sensitivity to supplemental irrigation at each growth stage.
According to the constructed BP crop-water model for supplemental irrigation with harvested rainwater,decreasing water supply led to reduced yields but higher relative yield indices,which can be explained by the general crop-water relationship(Table 3).Based on the sensitivity index,supplemental irrigation at the Heading-early milk growth stage had the greatest effect on increasing yield,and the smallest effect was found at the Emergence-jointing stage.On the other hand,the simulation results also confirmed the beneficial effect from water withholding(drought acclimation)at seedling stage on crop yield.Results in Table 3also showed that sensitivity of maize crop to water deficit status decreased in the following sequence:Heading-Early milk>Jointing-tassel>Milk-mature>Emergence-jointing stages.
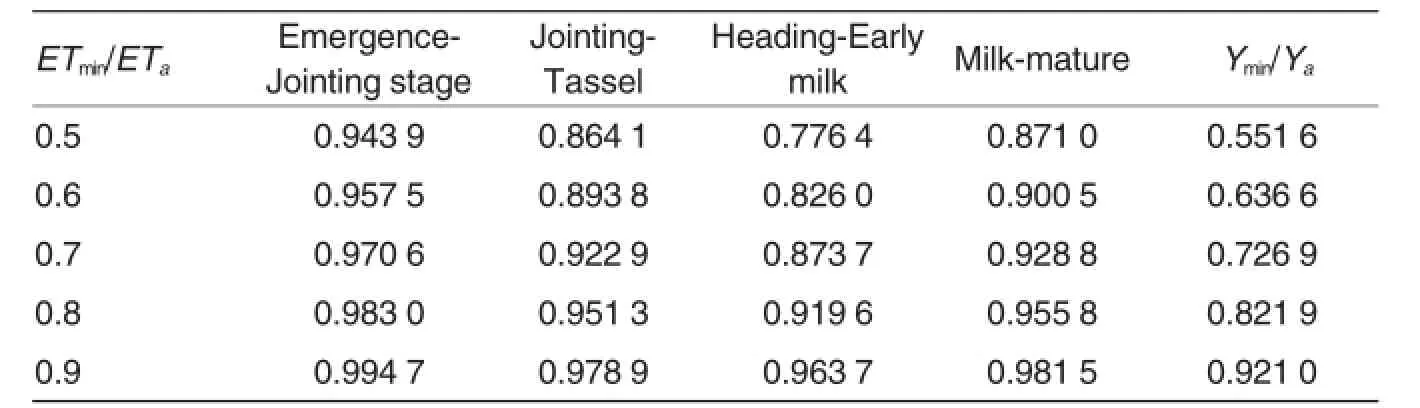
Table 3The indices of relative yield(Ymin/Ya)simulated using the BP Model
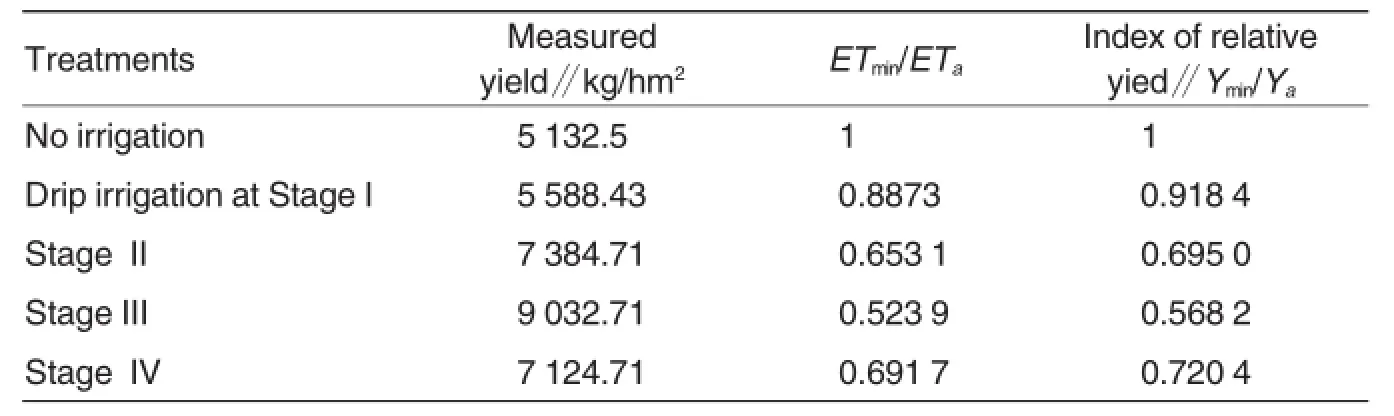
Table 4 The indices of relative yield(Ymin/Ya)of maize in 2007

Table 5 The indices of relative yields(Ymin/Ya)of measured maize yield and simulated data

Table 6 The water deficit sensitivity index simulated using the Jensen model
Furthermore,the accuracy of the constructed BP neural network models was validated by comparing the predicted value to the actual maize yield. To simplify the process,the treatments in 2007 were drip irrigation at growth stages 1,3 and 4.The actual yield index at the corresponding stages was ETmin/ETa=0.887 3,ETmin/ETa= 0.523 9,and ETmin/ETa=0.691 7,and the predicted value for the respective counterpart was ETmin/ETa=0.9, ETmin/ETa=0.5,and ETmin/ETa=0.7 (Table 4).Error between the predicted and actual yields was less than 3% (Table 5),which confirmed that the predicted yield is very close to the actual measurement.Therefore,the BP neural network crop-water model for supplemental irrigation with harvested rainwater can be used to simulate the relationship between supplemental irrigation at various growth stage of maize and the final yield under extreme water deficit condition.
The transformed Jensen model
To test the applicability of the transformed Jensen model,a multivariate regression program was written in MatLab language to obtain the sensitivity indices at all the growth stages(Table 6).Five schemes were designed to predict maize yield at different levels and timing of supplemental irrigation.
The sensitivity index is 0.027 1 at Emergence-jointing,0.269 0 at Jointing-tassel,0.337 3 at Heading-early milk,and 0.255 9 at Milk-nearly mature stage.Then five supplemental irrigation schemes consisting of different amounts of water and at different crop growth stages were designed to predict yields under each of the scenarios(Table 7).The measured maize yield in 2007 and the simulated yield using the transformed Jensen models are presented in Table 8.The relative error between the two sets of yield data was below 5%which is higher than the 3%error level using the BP neural network model.In general,the predicted maize yields using the two models were very close to each otheras well as to the actual yield,and the BP neural network model is slightly better than the transformed Jensen model.
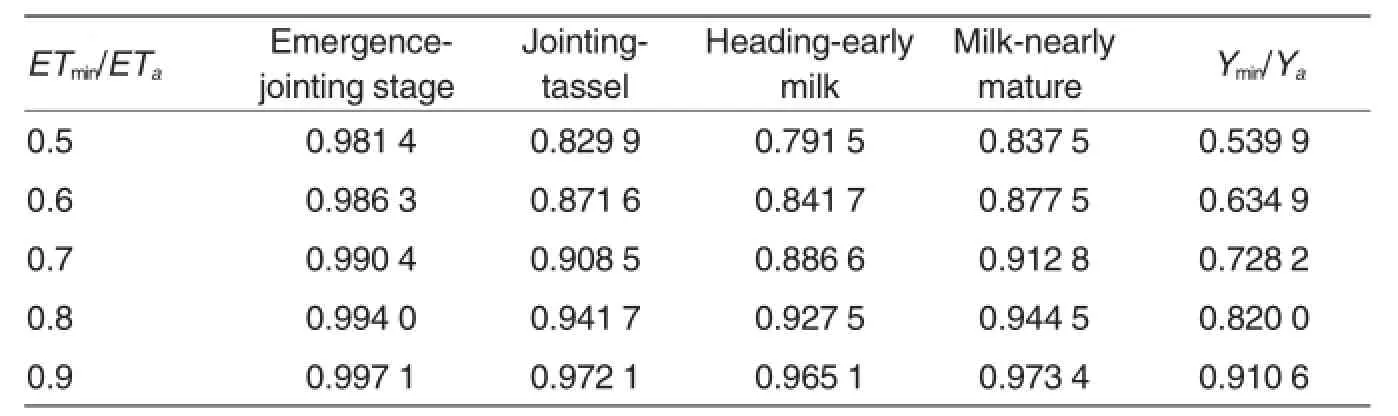
Table 7 The predicted relative yield index using the transformed Jensen-model(Ymin/Ya)
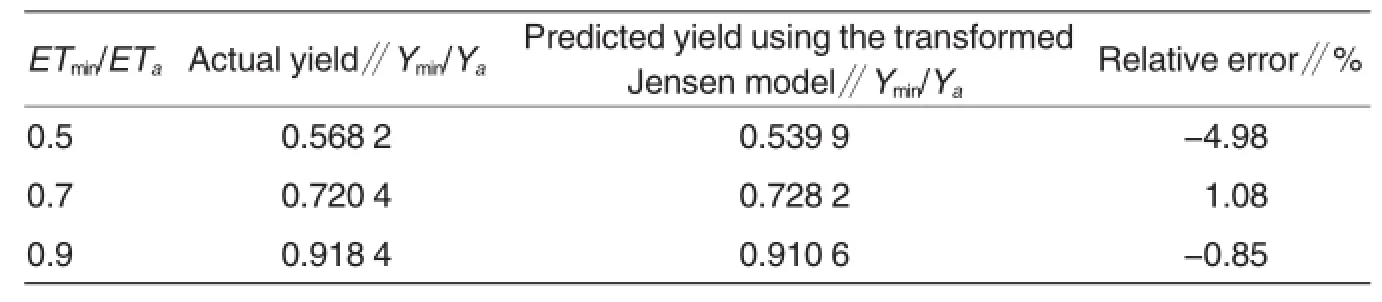
Table 8 The measured and simulated relative yield index(Ymin/Ya)of maize
According to the sensitivity index from the transformed Jensen Model, heading to milking stage is the most sensitive to water deficit(Table 6). The second most critical stage is the elongation-heading stage.These results agree to the simulated water deficit sensitivity index using the BP crop-water model for supplemental irrigation with harvested rainwater under extremely water deficit condition. Such a high level of correlation confirmed that the BP neural network crop-water model can be used to accurately simulate maize yield under various water deficit conditions.
Conclusions
(1)Supplemental irrigation at the flag leaf to grain filling stages has the most pronounced effect on improving maize yield.Moderate water constraint at seedling emergence-stem elongation stages will not cause obvious yield reduction.
(2)The BP neural network cropwater model for supplemental irrigation with harvested rainwater was able to simulate the generic relationship between yield and water status at various growth stages of maize crop.Both the BP and the transformed Jensen model predicted similar sensitive patterns to water deficit conditions at each of the maize growth stages.
(3)Compared to the transformed Jensen model,the BP neural network crop-water model was more accurate in simulating maize yield on the Loess Plateau.Thus the BP model system is preferred under such situation.But the experimental data for constructing the model were collected for a short period of time and from a small number of locations,the constructed model should be used only in areas with similar environmental conditions.
Furthermore,artificial neural network program has its inherent deficiencies,for instance the number of hidden layers and the hidden nodes have to be determined using the trial and error method.Additionally,parameters in the neural network model have not a physical meaning,they cannot represent the connections between component variables in the network.Future research needs to be focused on how to improve the BP neural network crop water-model and the network training methods.
[1]HERRMANN T,SCHMIDA U.Rainwater utilization in Germany:efficiency,dimensioning,hydraulic and environmental aspects[J].Urban Water,2000,1: 307-316.
[2]ROCKSTROM J,BARRON J,Fox P. Rainwater management for increased productivity among small-holder farmer in drought prone environments[J]. Physics and Chemistry of the Earth, 2002,27:949-959.
[3]SAZAKLI E,ALEXOPOULOS A,Leotsinidis M.Rainwater harvesting,quality assessment and utilization in Kefalonia Island,Greece[J].Water Research, 2007,41:2039-2047.
[4]PANIGRAHI B,PANDA S N,MAL B C. Rainwater conservation and recycling by optimal size on-farm reservoir[J]. Resources,2007,50:459-474.
[5]KAHINDA JM,LILLIE E S B,TAIGBENU A E,et al.Developing suitability maps for rainwater harvesting in South Africa[J].Physics and Chemistry of the Earth,2008,33:788-799.
[6]LEE JY,YANG JS,HAN M,et al.Comparison of the microbiological and chemical characterization of harvested rainwater and reservoir water as alternative water resources[J].Science of the Total Environment,2010,408:896-905.
[7]LI Z,BOYLE F,REYNOLDS A.Rainwater harvesting and grey water treatment systems for domestic application in Ireland[J].Desalination,2010,260: 1-8.
[8]LUO JJ,YANG FK,GAo SM.Suitable irrigation program for water-harvesting areas in semi-arid loess plateau[J]. Journal Irrigation and Drainage,2003, 22:25-28.
[9]WANG Y.Effect of the supplemental irrigation of harvested rainwater on dryland winter wheat yield and water use [J].Research of Soil and Water Conservation,2003,10:104-107.
[10]ZHANG ZS,WEI XH,LI XR,et al.Analysis on investment and benefit of harvested rainwater utilization in the northwest loess Plateau[J].Advances in Water Science,2004,15:813-818.
[11]LUIS R.SALADO-NAVARRO,THOMAS R.Sinclair.Crop rotations in Argentina:Analysis of water balance and yield using crop models[J].Agricultural Systems,2009,102:11-16.
[12]ALI REZA SEPASKHAH,SAGHAR FAHANDEZH-SAADI,SHAHROKH ZAND-PARSA.Logistic model application for prediction of maize yield under water and nitrogen management[J]. Agricultural Water Management,2011, 99:51-57.
[13]PATRICIO GRASSINI,HAISHUN YANG,SUAT IRMAK,JOHN THORBURN,CHARLES BURR,KENNETH G.CASSMAN.High-yield irrigated maize in the Western U.S.Corn Belt: II.Irrigation management and crop water productivity[J].Field Crops Research,2011,120:133-141.
[14]DOM NGUEZ A,MART NEZ R S, JUAN J A DE,MART NEZ-ROMERO A,TARJUELO J M.Simulation of maize crop behavior under deficit irrigation using MOPECO model in a semi-arid environment[J].Agricultural Water Management,2012,107:42-53.
[15]M.ABEDINPOUR,A.SARANGI,T.B. S.RAJPUT,MAN SINGH,H. PATHAK,T.AHMAD.Performance evaluation of Aqua Crop model for maize crop in a semi-arid environment [J].Agricultural Water Management,2012,110:55-56.
[16]MR SALAZAR,JE HOOK,A GARCIA Y GARCIA,JO PAZ,B.CHAVES,G. HOOGENBOOM.Estimating irrigation water use for maize in the Southeastern USA:A modeling approach[J].A-gricultural Water Management,2012. 107:104-111.
[17]GUO QS,LEI ZD,YANG SX.Senstive Index of Jensen’s Water Production Function Model of Wheat[J].Advances in Water Science,1996,7:20-25.
[18]WANG YR,LEI ZD,YANG SX.Cumulative function of sensitive index for winter wheat[J].Journal of Hydraulic Engineering,1997,5:28-35.
[19]JIAO XY,PENG SZ.Reasons and Solutions of Negative Values of Sensitive Indexes of Jensen’s Model[J].Journal of Shen Yang Agriculture University, 2004,35:439-442.
[20]ZHOU ZW,SHANG SH,LEI ZD. Jensen model and ANN model for water—fertilizer production function of winter wheat[J].Advances in Water Science,2003,14:280-284.
[21]CUI YL,MA CX,SHEN XZ,et al.Predicting reference evaportranspiration based on artificial neural network with genic arithmetic[J].Advances in Water Science,2005,16:76-81.
[22]GUO XP,ZHU CL.Model of crop response to water with influence of after—effect of water stress[J].Advances in Water Science,2004,15: 463-466.
[23]WEI ZM,CHEN YX,SHI HB,et al. Preliminary study on spring wheat response to water with BP neural network method[J].Journal Irrigation and Drainage,2002,21:12-16.
Responsible editor:Xiaoxue WANG
Responsible proofreader:Xiaoyan WU
Supported by Inner Mongolia water conservancy"Twelfth five-year"Major Science and Technology Demonstration Project-scientific Support Project for New Water-saving Irrigation Area of Four ten Million mu in Inner Mongolia in China(20121036)and the National Natural Science Foundation of China(No.51469026,2012MS0621)and the Guided Reward Fund for Scientific and Technological Innovation,Inner Mongolia,China.
*Corresponding author.E-mail:lixinggmm@163.com
Received:March 3,2015 Accepted:April 17,2015
杂志排行
Agricultural Science & Technology的其它文章
- Studies on the Influences of Different Planting Patterns on the Emissions of Methane and Nitrous Oxide in the Paddy Field
- Effects of Exogenous Glycine Betaine on Oxidation Metabolism in Cucumbers during Low-temperature Storage
- A Preliminary Study on Genetic Variation of gE Gene of an Epidemic Pseudorabies Virus Strain and Its Pathogenicity to Piglets
- Development and Application of a Quantitative Competitive PCR Assay for Detecting Mycoplasma hyopneumoniae
- A New Rapid and Batch-oriented Crushing Method for DNA Extraction from Maize Leaves
- Effects of Reducing Application Amount of Base Fertilizer and Increasing Application Time of Leaf Fertilizer on Corn Yield
