多输出模型确认中的混合矩指标*

赵录峰，吕震宙，张磊刚，王新维

(1.西北工业大学 航空学院， 陕西 西安　710072； 2.中国运载火箭技术研究院， 北京　100076;

3.中国人民解放军93363部队, 辽宁 沈阳　110141)



多输出模型确认中的混合矩指标*

赵录峰1，吕震宙1，张磊刚2，王新维3

(1.西北工业大学 航空学院， 陕西 西安710072； 2.中国运载火箭技术研究院， 北京100076;

3.中国人民解放军93363部队, 辽宁 沈阳110141)

摘要：在不确定性条件下，同时考虑到多维输出之间的相关关系和单输出的均值，构建由多输出数学期望列阵和协方差矩阵组成的多输出模型确认局部混合矩指标和全局混合矩指标。其中局部混合矩指标包括绝对指标(LA-3M)和相对指标(LR-3M)，它们适合单点位置的多输出局部模型确认；全局混合矩指标也包括绝对指标(GA-3M)和相对指标(GR-3M)，它们适合多点位置的多输出全局模型确认。通过数字算例和工程算例，所提指标可行有效，能够方便地度量计算模型和物理实验之间的差异程度。

关键词：模型确认；混合矩；多输出模型；相关性；不确定性

随着计算机仿真技术的飞速发展和复杂产品工程实验费用的不断增加，很多复杂产品的物理实验逐渐被计算模型所替代。计算模型是对真实物理过程的一个抽象描述，但建模过程受各种不确定性因素的影响，模型预测与物理实验结果之间可能存在一定的差异。如何科学地定量度量它们之间的差异程度，是当前“模型确认”领域的重点研究内容，也是国内外学术界和工业界普遍关注和讨论的热点。模型确认被定义为：“从目标用途角度出发，客观地评估计算模型在多大程度上准确描述真实物理过程”[1-3]。在模型确认过程中，首要的核心问题是构建一个“模型确认指标”，该指标要求能够科学有效地定量度量计算模型和实际物理过程之间的差异程度。模型确认指标被定义为“用来度量模型响应量与实验结果之间差异程度的指标”[4-5]。它是模型确认工作的基础和依据，在工程设计与分析领域，广泛用于多模型方案决策、模型预测能力评估和模型校准效果评价等工作之中。因此，开展模型确认指标研究，对推进模型确认工作的科学发展，提高计算机数字仿真技术的工程应用水平具有重要的理论价值和实践意义。

近几年国内外学术界对模型确认指标进行了大量研究，文献[6]对现有指标进行了系统分类和分析。根据模型的关键特性，模型确认指标可分为不同的类型。按不确定性类型，模型确认指标可分为确定型和不确定型指标[7-8]；按响应量的数目，可分为单输出和多输出指标；按输入可控变量的位置，可分为单点位置和多点位置指标。本文主要研究不确定性条件下的模型确认指标构建问题。概括起来，现有的不确定性条件下的模型确认指标，主要分为四类：假设检验类、贝叶斯因子类、频率类和面积类。通过对比分析，这些指标都有各自的优缺点及适用范围。文献 [6,9]分别运用假设检验和贝叶斯方法开展模型确认工作，这两种方法都是在一定置信水平下对模型预测与实验结果的一致性进行判断，但没有对它们之间差异程度进行定量度量，实质上是一种定性与定量相结合的方法，并不是严格意义上的模型确认过程。文献[1]提出的频率指标是对一定置信水平下模型预测与实验结果均值之间距离的度量，这一指标虽然是一种严格意义上的模型确认指标，且便于设计人员理解，但由于没有考虑响应量的方差和相关性，因此仅适合响应量分布中心发生偏离情况下的模型的确认。文献[1,8,10]运用模型输出响应量与实验结果经验分布函数之间的面积差异，提出了直接面积和u-pooling两种模型确认指标，适合于单维和多维独立响应量的模型确认，但由于该方法建立在求解响应量边缘分布面积差异的基础之上，没有考虑到多维响应量之间的相关性，因此不适合多维相关响应量的模型确认问题。为了解决这一问题，文献[11]在直接面积和u-pooling指标的基础上，应用多维概率积分转换方法，提出了概率积分转换(Probability Integral Transformation,PIT)和t-pooling模型确认指标，分别适合多维相关响应量在单点位置和多点位置的模型确认。虽然这一指标在多维相关响应量模型确认方面具有一定的优越性，但也存在一定的缺陷。一是该指标采用多维概率积分转换方法，压缩了大量信息，存在评估过度和评估不足的风险；二是该指标属于无量纲指标，物理意义不明确，不便于工程人员理解和使用；三是当实验数据不足时，无法正确地求解多输出响应量的联合分布函数，从而使得该指标较难应用。为此，本文针对多维相关响应量的模型确认问题，依据随机变量各阶矩的优良特性，提出了一种物理意义相对明确且便于使用的基于混合矩的多维相关模型确认指标。

1混合矩模型确认指标构建

1.1　多输出模型确认特点分析

不确定性条件下，如果将多输出计算模型的输入变量或参数(如：载荷、几何尺寸或边界条件等)看作随机变量，那么它们的输出响应量(如：应力、应变、挠度或加速度等)也是多维随机变量；同理，物理实验数据也属于多维随机变量。因此，依据概率论和数理统计相关理论，不确定性条件下多输出模型确认指标实质上就是对多维计算模型输出响应量的联合概率分布与实验结果所服从的联合概率分布之间的差异程度的度量[9]。

然而，在物理实验和数学建模过程中，受随机因素和人的认知能力影响，多输出模型确认指标的构建比较复杂，面临多种情况的挑战[1]。一是多输出响应量的物理意义可能不同，各自的量纲存在差异。如有的响应量用空间指标(应变、挠度)度量，有的用时空指标(速度、加速度)度量。二是多维响应量之间可能具有相关性。当多输出模型具有相同的输入变量，或输入变量之间存在很强的相关性时，这些输入变量之间的相关性就会传递到输出响应量，使得输出响应量之间存在很强的相关关系。三是多维输出响应量的输入变量可能是可控变量，也可能是随机变量。可控输入变量在一定时空范围变化[12]，当它在单点位置时，多维输出响应量服从某一联合概率分布；当它在多个位置变动时，多维输出响应量所服从的联合概率分布随之发生变化。

1.2　多输出模型确认指标构建的数学基础

随机变量的数字特征是由随机变量的分布确定的，能够描述随机变量某一方面的随机取值特征的常数。对多维随机变量来说，最重要的数字特征是数学期望(一阶中心矩)、方差(二阶中心矩)和协方差(二阶混合矩)。数学期望描述随机变量取值的平均大小，方差描述随机变量与自身的数学期望的偏离程度，协方差描述随机变量之间的相互关系。数学期望、方差和协方差虽然不像分布函数、分布律和概率密度函数那样完整地描述随机变量，但它能够描述随机变量的重要方面或人们最关心的重要特征。由于不确定性条件下的多输出模型确认指标的本质是对模型输出响应量与实验观察值所服从的两个联合分布函数之间差异程度的度量，然而在实际工程应用中，物理实验观察值的分布函数一般很难准确求得，因此，多维模型确认指标可以运用这两个联合分布函数的数字特征之间的差异程度来表示。

(1)

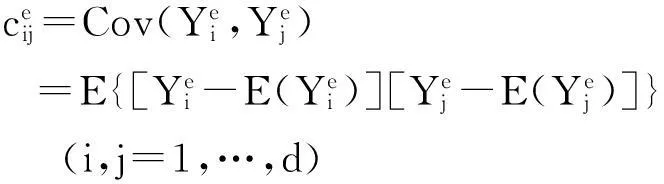
(2)

(3)

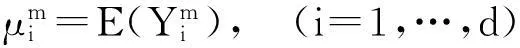
(4)

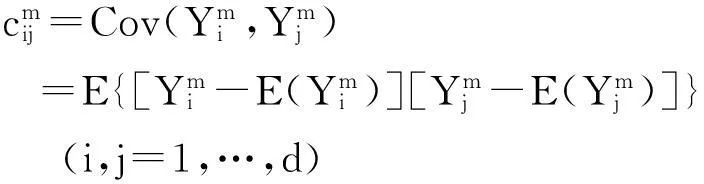
(5)

(6)

1.3　多输出模型确认指标的构建

依据多维随机变量各阶矩的性质，结合文献[1]和文献[10]提出的模型确认指标构建原则，分别建立了如式(7)和式(8)所示的局部混合矩模型确认绝对指标(Local Absolute Metric based on Mixed Moment for model validation，LA-3M)和全局混合矩模型确认绝对指标(Global Absolute Metric based on Mixed Moment for model validation，GA-3M)。当多输出模型的可控变量在单点位置时，可运用式(7)度量模型响应量与实验结果之间差异程度；当可控变量在多个位置变动时，则每一个单点位置对应的dLA(Ym,Ye)属于随机变量，因此，可运用dLA(Ym,Ye)的数学期望dGA(Ym,Ye)度量模型响应量与实验结果之间差异程度。

(7)

dGA(Ym,Ye)=E[dLA(Ym,Ye)]

(8)

(9)

dGR(Ym,Ye)=E(dLR(Ym,Ye))

(10)

上述确认指标不仅满足文献[1]和文献[10]所提的客观性、物理性、无界限、非负性、对称性、三角不等性和收敛性等基本要求，而且同时考虑了输出响应量的均值及二阶混合矩，合理地度量了计算模型与实验数据在均值、变异性及相关性等方面的差异程度，因此，该指标具有灵敏度高和便于工程应用等优良特性。

2混合矩模型确认指标的求解

基于混合矩方法的多输出模型确认指标求解的核心，是求解模型和实验输出响应量的一阶中心矩和二阶混合中心矩形成的协方差矩阵。下面依据大数定理，运用MonteCarlo数字模拟法求解。

2.1　单点位置指标求解

基于混合矩方法的单点位置多输出模型确认指标的求解流程如图1所示，求解过程可概括为4个步骤。

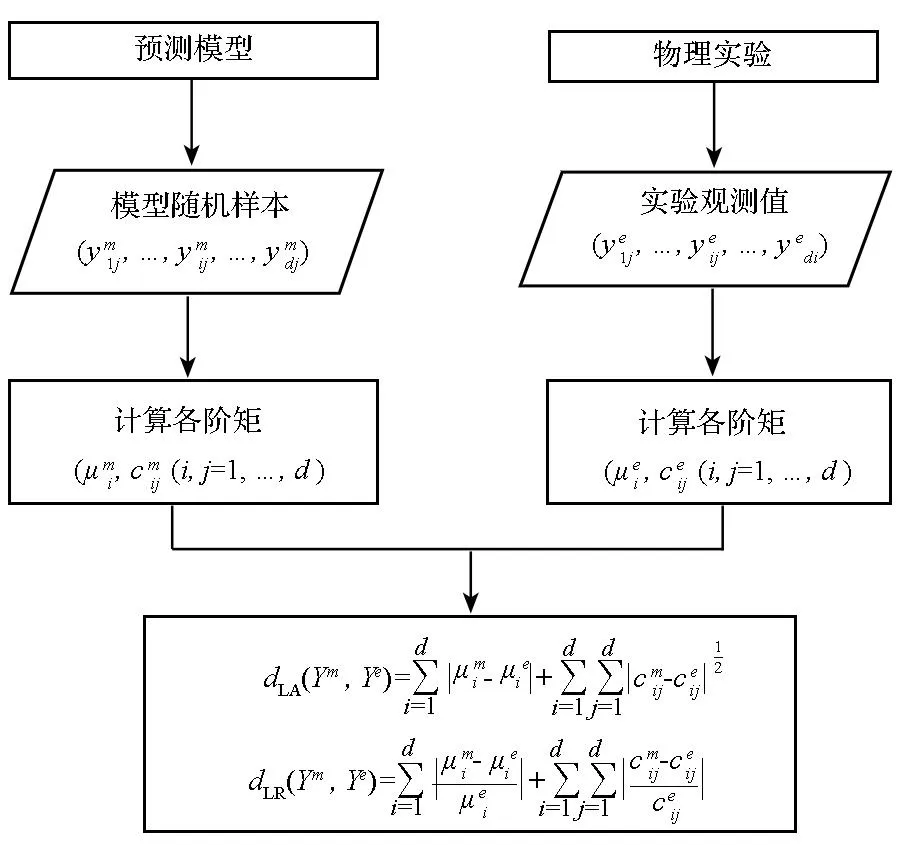
图1　单点位置多维响应量模型确认指标计算流程Fig.1　Flowchart of validation metric for models with multivariate output at a single validation site

步骤3：计算模型响应量和实验观测值的各阶矩。采用式(11)～(14) 计算模型响应量和实验观测值的各阶矩。

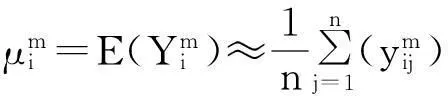
(11)

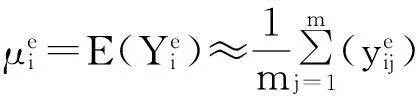
(12)

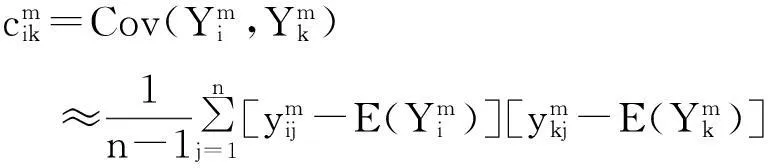
(13)

(14)

步骤4：求解模型确认指标。将求解所得的各阶矩带入式(7)和式(9)，可得到单点位置多维响应量模型确认指标dLA(Ym,Ye)和dLR(Ym,Ye)。

2.2　多点位置指标求解

多点位置指标求解建立在单点位置指标求解的基础之上，主要包括3个步骤。

步骤1：根据实验计划，确定k个不同位置的可控输入矢量xh，h=1,…,k。

步骤3：根据式(8)和式(10)求解多点位置的模型确认指标。其中dGA(Ym,Ye)和dGR(Ym,Ye) 分别由式(15)和式(16)求解。

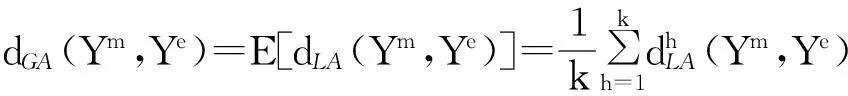
(15)

(16)

3算例分析

下面针对基于混合矩的多输出模型确认指标，通过两个算例验证它们的可行性和有效性。

3.1　算例1

本算例的物理实验数据通过下式获取：

(17)

式中：x(0≤x≤6)为可控变量，θ(θ=1.5)为模型参数，ε1～N(0,0.22)和ε2～N(0,0.22)为两个实验响应量的测量误差，ε1与ε2之间的相关系数ρε1,ε2=0.5。构建的预测模型共5个，它们分为两组(见表1)。设模型响应量的样本量用n表示，物理实验观测值的样本量用m表示。

表1 两个测试组预测模型

3.1.1测试1

包括3个预测模型。模型1与实验过程一致，是一个正确的模型；模型2的参数θ与实验模型有差异；模型3与实验模型相比，不仅模型参数θ发生了变化，而且相关系数也发生了变化。显然模型1的准确性高于模型2，模型2高于模型3。这组测试的目的：在模型参数或相关性存在差异的情况下，讨论所建指标的适应性、可行性和有效性。

3.1.1.1单点位置测试

m固定，n变化。在x=2.0处，按照2.1部分提出的单点位置指标求解方法和步骤，分别由式(17)生成m=1000组实验观测数据，由表1第一测试组模型生成n组模型响应量，其中n在区间[100，12 000]变化，计算模型确认指标值。不确定性条件下，指标值具有一定的随机性，指标均值的置信度为95%的置信区间随n的变化情况如图2、图3所示。

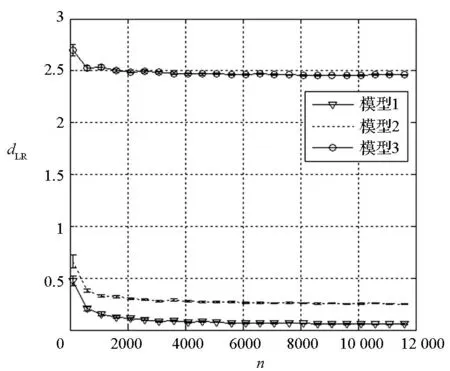
图2　dLR均值的置信区间在x=2.0处随n的变化曲线Fig.2　Confidence interval of the mean of dLRversus the n at validation site x=2.0

图3　dLA均值的置信区间在x=2.0处随n的变化曲线Fig.3　Confidence interval of the mean of dLAversus the n at validation site x=2.0

由如图2、图3可以看出，在单点位置，随着n的增大，模型确认指标dLA(Ym,Ye)和dLR(Ym,Ye)的均值及其置信区间都迅速减小，当n>2000时，它们趋于稳定状态，收敛到一个固定值或范围，这表明n>2000时，模型响应量的计算结果趋于它们的解析解，且3个计算模型与物理实验之间的差异程度也处于稳定状态。为了尽可能地提高模型响应量的计算精度，本文在模型确认指标的验证过程中，选取n=10 000作为模型响应量样本量。

n固定，m变化。在x=2.0处，按2.1部分提出的单点位置指标求解方法和步骤，由表1第一测试组模型生成n=10 000组模型响应量，由式(17)生成m组实验观测数据，其中m在区间[5，1000]变化，计算模型确认指标值。指标均值的置信度为95%的置信区间随m的变化情况如图4和图5所示。

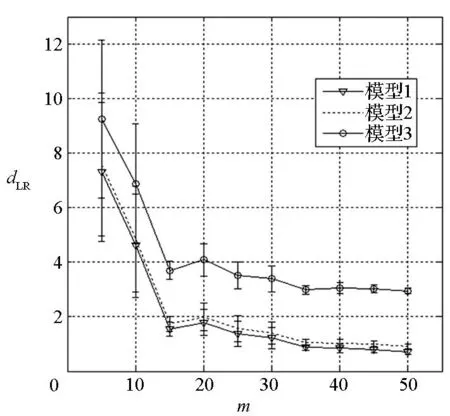
(a) m在区间[0,50]变化图(a) m varies on the interval [0,50]

(b) m在区间[50,1000]变化(b) m varies on the interval [50,1000]图4　dLR均值的置信区间在x=2.0处随m的变化曲线Fig.4　Confidence interval of the mean of dLRversus the m at validation site x=2.0

由图4，图5可以看出： 在单点位置，随着实验观测数据m的增大，模型确认指标dLA(Ym,Ye)和dLR(Ym,Ye)的均值及其置信区间都迅速减小；当m>200时，它们开始趋于收敛；当m=1000时，它们收敛到一个固定值或范围。

由图4(a)和图5(a)可以看出，当m在[5，50] 区间取值时，模型确认指标(尤其相对指标dLR)均值的置信区间较大，且相互重叠。这一现象表明当实验观测数据量过少时，运用该指标难以准确区分计算模型之间的优劣，存在判断错误的风险。因此，在实验数据过少，且实验数据误差过大的情况下，提出的模型确认指标具有一定的局限性。

(a) m在区间[0,50]变化(a) m varies on the interval [0,50]

(b) m在区间[50,1000]变化(b) m varies on the interval [50,1000]图5　dLA均值的置信区间在x=2.0处随m的变化曲线Fig.5　Confidence interval of the mean of dLA versus the m at validation site x=2.0

由图4(b)和图5(b)可以看出，当实验观测数据m>50时，局部混合矩模型确认指标都能够很好地度量计算模型与物理实验之间的差异程度，客观地评估计算模型之间的优劣。为了从理论上更好地验证所提指标的可行性和有效性，本文在模型确认指标的验证过程中，选取实验观测数据的样本量m=1000。

n固定，m固定。在x=2.0处，按2.1部分提出的单点位置指标求解方法和步骤，由式(17)生成1000组实验观测数据，由表1第一测试组计算模型生成10 000组模型响应量，计算模型确认指标，并与文献[11] 提出的PIT面积法指标进行对比，结果见表2。

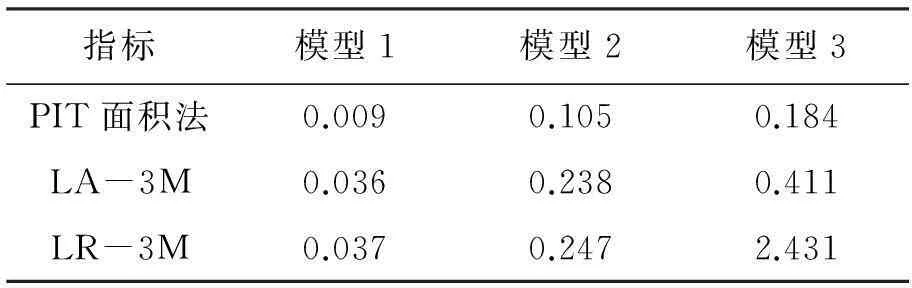
表2　单点位置第一测试组模型确认指标计算结果

3.1.1.2多点位置测试

可控制变量x在(0≤x≤6)的区间范围内，从0开始每间隔0.01取一个x值，即选取600个固定点。同理，对每个x值，由式(17)生成1000组实验观测数据，由表1第一测试组中的3个模型分别仿真生成10 000组模型响应量，按照2.2部分提出的多点位置指标求解方法和步骤，得到的多点位置的模型确认指标值，并与文献[11] 提出的t-pooling面积指标进行对比，结果见表3。

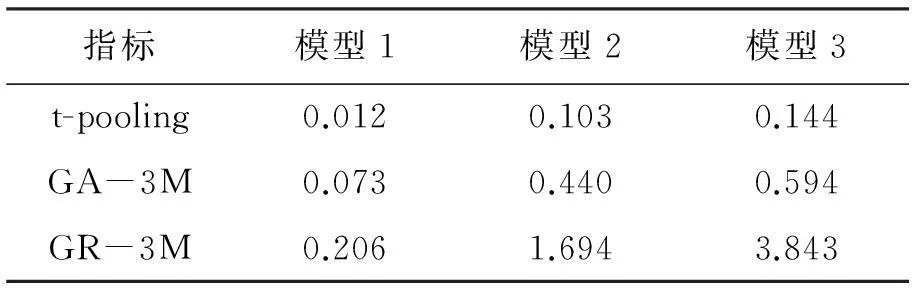
表3　多点位置第一测试组模型确认指标计算结果

本算例测试1中，通过表2和表3可以清晰地看出，无论在固单点位置，还是在多点位置，在模型参数和相关系数存在差异的情况下，本文提出的模型确认指标同PIT和t-pooling面积指标具有同样的效果，都能够客观地判断出模型1优于模型2，模型2优于模型3，这一结论与定性分析相符，达到第一组测试的目的，验证了所提指标的可行性和有效性。

3.1.2测试2

包括2个预测模型。模型4和模型5将确定性参数θ误作为不确定性变量，服从均值同为θ=1.5，方差不同的正态分布。其中模型4中θ的方差较小，而模型5中方差较大，显然模型4与实验数据的一致性高于模型5。第二组测试的目的：在模型参数的离散程度存在很小差异时，验证所建指标是否能够客观准确地度量计算模型与物理实验之间的差异程度。

3.1.2.1单点位置测试

在x=3.0处，按照2.1部分提出的单点位置指标求解方法和步骤，同理，由式(17)生成1000组实验观测数据，由表1第二测试组计算模型生成10 000组模型响应量，得到模型确认指标，并与文献[11] 提出的PIT面积指标进行对比，结果见表4。

3.1.2.2多点位置测试

在可控制变量x(0≤x≤6)的区间范围，从0开始每间隔0.01取一个x值，即选取600个固定点。对应于每个x值，由式(17)生成1000组实验观测数据，由表1第二测试组中的2个模型生成10 000组模型响应量，按照2.2部分提出的多点位置指标求解方法和步骤，得到模型确认指标值，并与文献[11] 提出的t-pooling面积指标进行对比，结果见表5。

表4　单点位置第二测试组模型确认指标计算结果

表5　多点位置第二测试组模型确认指标计算结果

本算例测试2中，由表4和表5可以清晰地看出，无论在单点位置，还是在多点位置，在确定性参数θ被错误地作为不确定性变量的情况下，本文提出的指标同PIT和t-pooling面积指标具有同样的效果，都能够明确地判断出模型4优于模型5，这一结论与定性分析吻合，达到第二组测试的目的，验证了本文所提指标的可行性和有效性。

对表2～5的计算结果进一步分析可以看出：基于混合矩的多输出模型确认相对指标(LR-3M和GR-3M)的灵敏度最高，而多输出模型确认绝对指标(LA-3M和GA-3M)与PIT和t-pooling指标的灵敏度处于同一水平，相对较低。按照模型确认指标构建原则，当模型1与实验模型完全一致时，其指标值应该为零。从表2和表3的结果来看，模型1的六个指标值都不为零，尤其GR-3M的偏差较大(0.206)，这一问题的原因不在于指标本身，而在于实验室数据和模型计算存在不确定性。如果进一步提高模型计算精度，增加实验数据量，减少实验误差，模型1的指标值最终会收敛于零。

3.2　算例2

如图6所示的矩形截面悬臂梁，自由端承受集中可控力，梁的长度L=2m，截面宽度b=50mm，截面厚度h=37mm，弹性模量E～N(206.8,10.52)，输出响应量为梁固定端A点的正应力σA(GPa)、自由端B点处截面的转角θB(rad)和挠度yB(mm)，实验数据由解析方程式(18)产生，它们的测量误差分别为εθ～N(0,0.0052)，εy～N(0,0.0052)，εσ～N(0,0.012)。

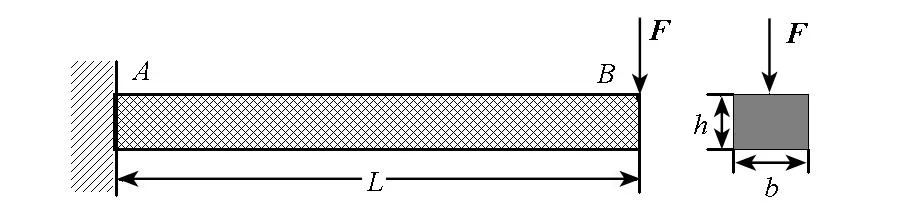
图6　悬臂梁结构Fig.6　Diagram of the cantilever beam structure

(18)

为节约实验费用，提高效率，工业部门建立了3个不确定条件下的悬臂梁模型，这些模型的形式与解析方程相同，但各随机变量的分布函数或分布参数存在差异，具体情况见表6。

表6　悬臂梁输入随机变量的分布参数

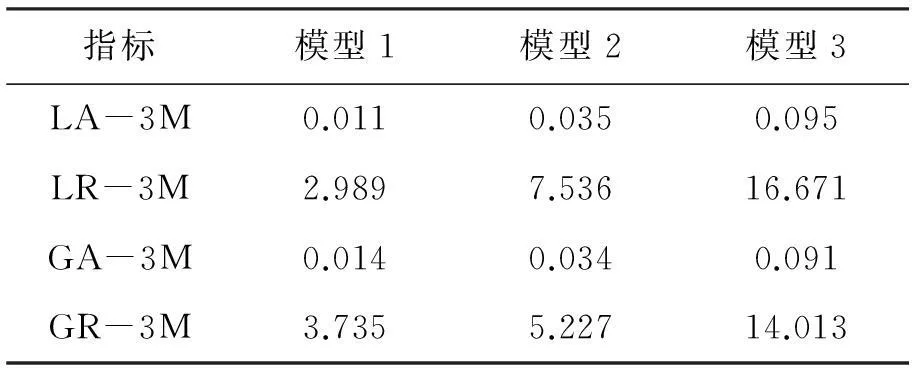
表7　悬臂梁模型确认指标计算结果

由表7可以看出，无论在单点位置，还是在多点位置，运用本文提出的模型确认指标都能够明确判断出模型1优于模型2，模型2优于模型3，这一结论与定性分析结果吻合，从而再次验证了所提指标的可行性和有效性。

4结论

基于混合矩的多输出模型确认绝对指标和相对指标及求解方法，能够有效度量模型响应量与实验结果之间差异程度。

1)由于采用了工程人员比较熟悉且便于应用的各阶矩作为指标的组成要素，使得该指标具有工程应用方便、物理意义明显和分辨率高等优点。

2)指标既适合单输出模型确认，也适合复杂的具有相关关系的多输出模型确认，可以直接用于工程设计与分析、多模型方案决策、模型预测能力评估和模型校准效果评价等工作之中，对推进工程建模的建设和发展具有重要意义。

3)指标及其求解方法也存在一定的局限性：一是当实验数据过少且误差过大，或模型计算结果不准确时，指标计算结果会产生一定的偏差。二是指标求解方法是一种比较简单的方法，在提高求解效率和准确性方面，指标的求解方法还有待于进一步深化研究。

参考文献(References)

[1]Oberkampf W L, Barone M F. Measures of agreement between computation and experiment: validation metrics[J]. Journal of Computational Physics, 2006, 217(1): 5-36.

[2]Oberkampf W L, Sindir M,Conlisk A. Guide for the verification and validation of computational fluid dynamics simulations[J]. AIAA,1998.

[3]Oberkampf W L, Roy C J. Verification and validation in scientific computing[M].New York,USA：Cambridge University Press, 2010.

[4]Xiong Y, Chen W, Tsui K L,et al. A better understanding of model updating strategies in validating engineering models[J]. Computer Methods in Applied Mechanics and Engineering, 2009,198(15-16): 1327-1337.

[5]Messer M, Panchal J H, Krishnamurthy V,et al. Model selection under limited information using a value of information based indicator[J]. Journal of Mechanical Design, 2010,132(12): 1-13.

[6]Liu Y, Chen W, Arendt P,et al. Toward a better understanding of model validation metrics[J]. Journal of Mechanical Design, 2011,133(7): 1-13.

[7]Schwer L E. Validation metrics for response histories: perspectives and case studies[J]. Engineering with Computers, 2007,23(4): 295-309.

[8]Ferson S, Oberkampf W L. Validation of imprecise probability models[J]. International Journal of Reliability and Safety, 2009, 3: 3-22.

[9]Rebba R, Mahadevan S. Validation of models with multivariate output[J]. Reliability Engineering and System Safety, 2006, 91(8): 861-871.

[10]Ferson S, Oberkampf W L, Ginzburg L. Model validation and predictive capability for the thermal challenge problem[J]. Computer Methods in Applied Mechanics and Engineering, 2008, 197(29-32): 2408-2430.

[11]Li W, Chen W, Jiang Z, et al. New validation metrics for models with multiple correlated responses[J]. Reliability Engineering and System Safety, 2014, 127:1-11.

[12]Jiang X M, Mahadevan S. Bayesian validation assessment of multivariate computational models[J]. Journal of Applied Statistics, 2008, 35(1):49-65.

http://journal.nudt.edu.cn

Mixed moment validation metric for models with multivariate output

ZHAOLufeng1,LYUZhenzhou1,ZHANGLeigang2,WANGXinwei3

(1.School of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China;

2. China Academy of Launch Vehicle Technology, Beijing 100076, China; 3. The PLA Unit 93363, Shenyang 110141, China)

Abstract：Considering the relations among multi-outputs and the mean of single output, the mathematical expectation of single dimensional variable and covariance metric of multi-dimensional variables were introduced into the validation metrics for models. The new metrics of LA-3M and LR-3M were proposed for validating multi-responses at a single validation site, while the metrics of GA-3M and GR-3M were proposed to collect data of multiple responses observed at multiple validation sites. These metrics were examined through a numerical test case and an engineering example to illustrate their feasibility and effectiveness. Results show that the proposed metrics are efficient and they can easily measure the differential degree of multiple responses between calculation model and physical experiment.

Key words：model validation; mixed moment; models with multivariate output; correlation; uncertainty

中图分类号：TB114.3

文献标志码：A

文章编号：1001-2486(2015)06-061-08

作者简介：赵录峰(1973—)，男，陕西富平人，博士研究生，E-mail：zlf315611@126.com；吕震宙(通信作者)，女，教授，博士，博士生导师，E-mail：zhenzhoulu@nwpu.edu.cn

基金项目：国家自然科学基金资助项目(51475370)；高等学校博士学科点专项科研基金资助项目(20116102110003)

收稿日期：*2015-01-09

doi:10.11887/j.cn.201506013