高陡度非球面磨削亚表面损伤深度规律*

朱登超,戴一帆,关朝亮,王贵林

(1. 国防科技大学 机电工程与自动化学院， 湖南 长沙　410073；

2. 超精密加工技术湖南省重点实验室, 湖南 长沙　410073)



高陡度非球面磨削亚表面损伤深度规律*

朱登超1，2,戴一帆1，2,关朝亮1，2,王贵林1，2

(1. 国防科技大学 机电工程与自动化学院， 湖南 长沙410073；

2. 超精密加工技术湖南省重点实验室, 湖南 长沙410073)

摘要：具有高陡度非球面特性的光学元件可以明显改善光学系统的空气动力学性能, 从而提升和优化系统综合性能。磨削加工方法可以作为此类元件的前期加工工序，而磨削难免会造成零件的亚表面损伤，且在这种高陡度非球面磨削加工中磨削参数是实时变化的，造成整个工件亚表面损伤深度不一致。针对这种情况，建立亚表面损伤预测模型，并结合半球形砂轮磨削的特点，通过理论计算预测非球面磨削亚表面损伤深度分布规律。在此基础上，以热压多晶氟化镁平面为对象进行模拟参数实验，通过磁流变抛斑点法得到各组参数下亚表面损伤深度情况，结果显示损伤深度范围在12.79μm～20.96μm之间，且沿试件半径方向由内向外呈增大趋势，结果与预测模型相吻合。

关键词：高陡度非球面；亚表面损伤；预测模型；热压多晶氟化镁

随着现代航空航天及武器系统技术的发展, 具有高陡度非球面特性的光学元件的应用越来越广泛。此类元件除了能满足光学系统自身光学功能外, 还能满足空气动力学等非光学要求, 从而达到提升和优化系统综合性能的目的。但其高陡度非球面(尤其是凹面)的外形特征给加工制造带来巨大挑战[1-2]。

目前研究和应用较广泛的红外光学材料较多，如金刚石、蓝宝石、尖晶石等，由于这些材料都具有高硬度的特点，进行高陡度非球面加工还存在很大的困难。热压多晶氟化镁材料也是目前使用最为广泛的红外窗口和整流罩材料之一，其熔点为1255℃，在波长为0.7μm～9μm，尤其是在3μm～5μm中红外波段具有良好的透过性能，还具有较好的抗热冲击性和耐化学腐蚀性[3-5]，同时该材料的硬度相对于前面几种材料都要低，容易实现高陡度非球面零件的低损伤加工。

磨削方法是实现高陡度非球面类光学元件加工的关键环节之一，主要作为工件前期粗加工工艺。但是磨削加工难免会造成零件的亚表面损伤，并且由于此类零件加工中砂轮和工件线速度是实时变化的，导致作用在工件上的磨削力实时变化，从而造成工件亚表面损伤深度不一致，影响后续加工。

1高陡度非球面磨削损伤预测

1.1　磨削系统设计

根据加工对象高陡度和非球面特点的要求，磨削工具需要使用半球形的小砂轮，设计的磨削装置示意图如图1所示。该磨削系统是以超精密车床为基础建立的，其中工件安装在回转主轴上，并沿X轴方向做水平运动；砂轮安装在磨轴上，并通过转接装置沿Z轴做水平运动。加工过程中，工件沿主轴做回转运动，同时X轴和Z轴执行联动控制，从而实现高陡度回转对称非球面的加工。

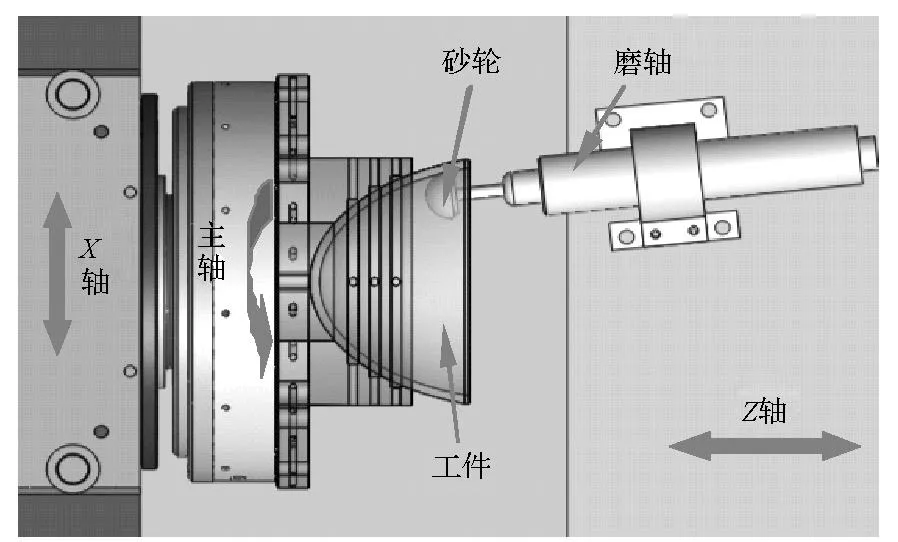
图1　高陡度非球面磨削加工装置示意图Fig.1　Sketch of grinding system for deep aspheric surface

1.2　损伤深度预测模型

为研究材料磨削损伤，首先建立损伤深度预测模型。磨削力是反映磨削过程的基本特征的主要因素之一，它与被加工材料的属性、磨削用量、砂轮类型及磨削液的选用等都有着密切关系，同时也会对磨削损伤深度造成较大的影响。众多学者对磨削力与磨削损伤深度之间的关系做了大量研究工作，其中日本学者Inasaki提出了单颗磨粒法向磨削力Fn与磨削损伤深度δ的校正关系[6]：

Fn∝δm

(1)

对于不同的磨削条件，指数项m的取值范围是0.5～1.5。而单颗磨粒承担的法向磨削力大小与磨粒的最大未变形切削深度有关，可以表示[7]为：

Fn=(αK0ag)2(1-ε)

(2)

其中，α为磨削力分力比，对于给定的磨削条件该值为常数，K0和ε为与试件材料特性相关的常量，ag为磨粒的最大未变形切削深度，其计算结果[7]表示为：

(3)

其中，vw，vs，ap，rs分别为工件磨削点线速度、砂轮磨削点线速度、砂轮磨削深度和砂轮半径。C表示砂轮表面磨粒密度，η表示切屑宽度与未变形切屑平均厚度之比。

综合式(1)～(3)可以得到损伤深度与各磨削影响因素的关系：

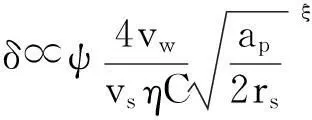
(4)

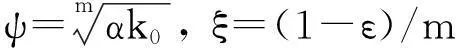
由上述模型可知：磨削损伤深度与工件磨削点线速度vw和磨削深度ap成正比关系，与砂轮磨削点线速度vs、切屑宽度和未变形切屑平均厚度之比η、砂轮表面磨粒密度C和砂轮半径rs成反比关系。

1.3　关键参数对损伤深度的影响分析

当以高陡度的非球面为磨削加工对象时，单次磨削过程中参数ap，C以及rs一般为恒定值，而η的大小与ap，rs以及材料属性有关，所以在这种条件下也是定值。因此，在高陡度的非球面磨削加工中，实际影响工件亚表面损伤深度的主要因素是工件磨削点线速度vw和砂轮磨削点线速度vs，则根据式(4)可知，损伤深度的大小与vw和vs的比值成正比。

采用球形砂轮磨削加工高陡度非球面时，为避免砂轮线速度为零的顶点位置参与磨削加工，砂轮轴线与工件光轴之间需要存在一定夹角，磨削加工示意图如图2所示。图中ωs表示加工时砂轮转速，ωw为工件转速，r为垂直工件光轴方向的径向坐标，fw为沿加工方向的进给速度，θ表示砂轮轴与工件轴的夹角，β表示在工件任意磨削点处的法线与工件轴的夹角。则工件在磨削点线速度可以表示为：

vw=2πrωw

(5)

图2　高陡度非球面磨削示意图Fig.2　Sketch of deep aspheric surface grinding

砂轮磨削点的线速度为：

vs=2πrsωssin(θ+β)

(6)

回转对称非球面的数学方程可表示为：

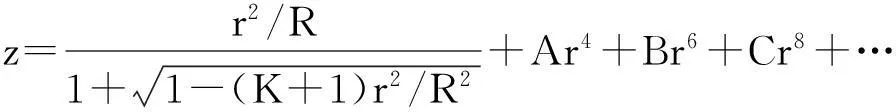
(7)

其中，R为顶点曲率半径，K为非球面的二次常数。式(7)中后面各项表示非球面的高次项，当只取右边第一项时，表示严格的二次曲面。根据几何关系可以确定β角与径向坐标之间的关系：

β=arctan(dz/dr)

(8)

其中“dz/dr”为z的一阶导数，表示斜率。综合式(5)～ (8)可以计算出工件线速度和砂轮线速度的比值：

(9)

结合加工经验，选取一定的工艺参数：工件转速100r/min、砂轮转速10 000 r/min，所选取砂轮半径为8mm，再结合曲面方程即可分别得到工件、砂轮磨削点线速度以及两者的比值沿工件径向方向的大小分布规律，结果分别如图3所示。

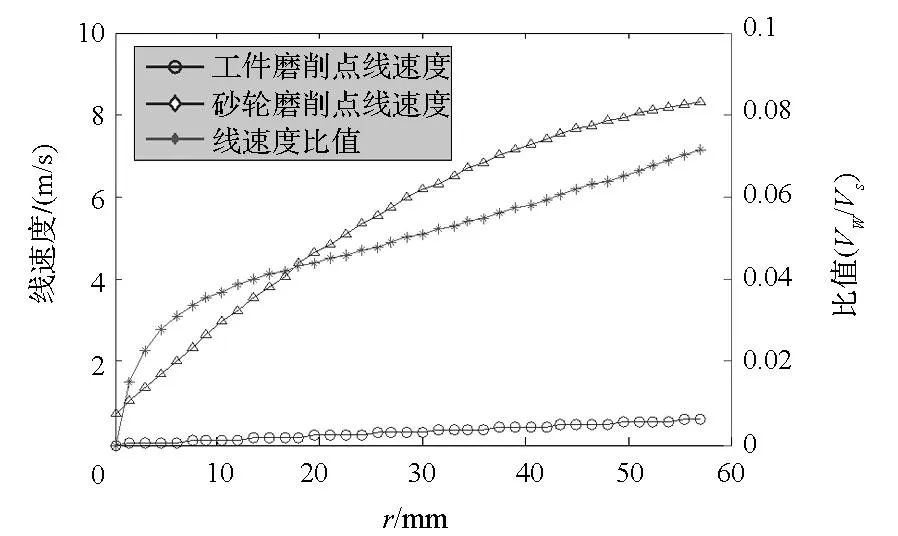
图3　磨削点线速度及其比值分布规律Fig.3　Regularity of velocities and the ratio at grinding point

从图3中线速度比值曲线可以看出，当径向坐标趋近于零时，砂轮线速度也越来越小，并接近于零，此种状态是磨削加工中的极端情况，这里暂时不做过多考虑。当径向坐标r较大时，工件线速度和砂轮线速度的比值随r的增大而增大，且呈近似线性关系。由此分析，可以确定以此种磨削方式加工高陡度非球面时，工件表面损伤深度随径向坐标的增大逐渐增大。

2磨削实验与检测结果分析

上面建立了小磨头磨削方式加工高陡度非球面零件时工件表面损伤深度的预测模型。接下来基于自主设计的小磨头磨削装置系统，以热压多晶氟化镁材料为对象开展验证实验。直接检测高陡度非球面的表面损伤深度比较复杂，且检测深度值不够准确。由于本文研究对象的最小曲率半径(40mm)相对于砂轮半径(8mm)来说较大，所以在假设砂轮轴刚度足够大，从而不考虑磨削力方向实时变化对实验的影响的情况下，可以采用平面试件近似替代高陡度非球面开展初步实验。为了保证实验的准确性，平面加工试验参数均模拟非球面加工时的参数。

2.1　试验的建立

试验采用的磨削加工方式与图1所示方式相同，只是将工件替换为平面试件。采用的试件口径为Φ100mm，砂轮采用青铜基金刚石磨粒半球形砂轮，粒度为240#，砂轮球形半径为8mm。砂轮轴与工件轴夹角为45°，砂轮转速通过砂轮线速度和砂轮形状来确定。磨削液采用水溶性陶瓷玻璃专用磨削液。实验在自研超精密车床UPL450上进行。

本试验共设计了10组加工参数，将工件分成10个环带进行加工，每个环带宽度为5mm，具体规划如图4所示。磨削参数中磨削深度和进给量均为恒定值，分别选15μm和20μm/r，则每组参数的变量为工件速度和砂轮速度。根据加工经验，工件转速定为100r/min，则工件由内向外不同径向坐标位置的线速度从0m/s线性增大到0.52m/s。然后以每个环带中间位置的线速度为参考，根据图3中所示工件与砂轮线速度关系曲线来确定不同环带对应的砂轮线速度，再通过控制砂轮转速来实现砂轮线速度的控制。具体参数设置在表1中列出，然后按照该参数开展了加工试验。

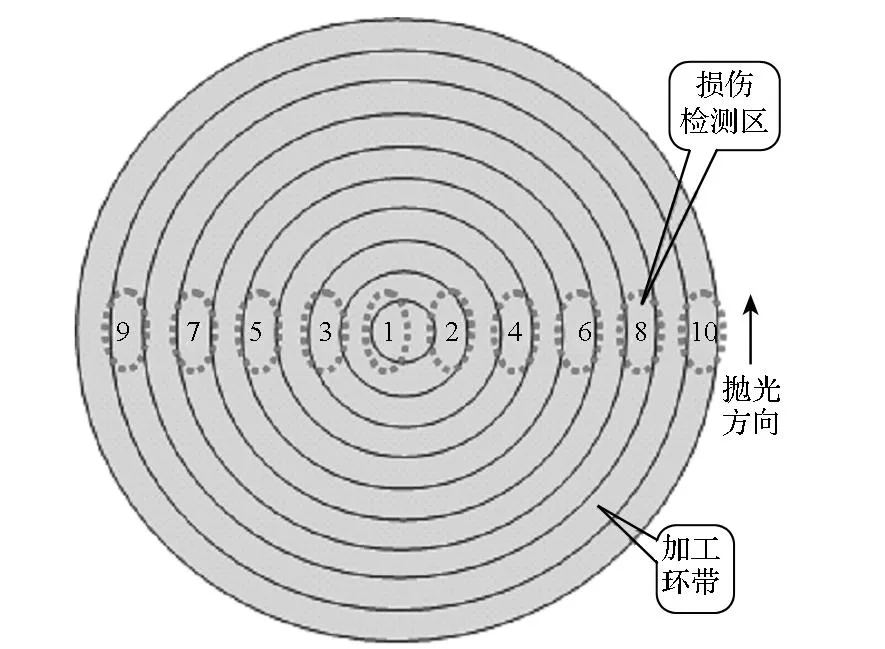
图4　加工和亚表面损伤深度检测分组规划Fig.4　Programming for machining and test of sub-surface damage depths

2.2　亚表面损伤深度检测及结果分析

试件磨削加工完成后，接下来需要检测各组参数条件下工件亚表面损伤深度。目前有多种方法可以实现材料亚表面损伤深度的测量，如：截面显微法、角度抛光法、磁流变抛光斑点法、磁流变抛光斜面法以及X射线衍射法等。结合本实验试件特点和现有条件，这里选用了磁流变抛光斑点法。该方法由Randi[8]等提出，其原理是利用磁流变抛光斑点将损伤深度方向的微米级测量转化为损伤在水平方向延伸距离的毫米级测量。该方法对亚表面损伤的放大可达数百倍，较大程度上提高了测量精度。

本实验具体测量方法分为以下几个步骤：第一，将试件安装到磁流变机床上抛斑点。由于工件上每一加工环带宽度只有5mm，而磁流变斑点宽度一般大于5mm，为了避免抛光斑点的相互干涉，并且方便后续测量，这里将抛光斑点沿工件直径方向交叉排布，具体分布为图4中虚线包含的10个区域。第二，利用轮廓仪检测各个斑点中线位置沿抛光方向的轮廓形貌。第三，采用高倍光学显微镜观察抛光斑点中线位置沿抛光方向的表面缺陷分布情况，同时使用精密微动平台记录从抛光起点位置到表面缺陷消失位置的总距离。最后，根据记录的距离对照每个斑点中线轮廓形貌即可得到亚表面损伤深度值。

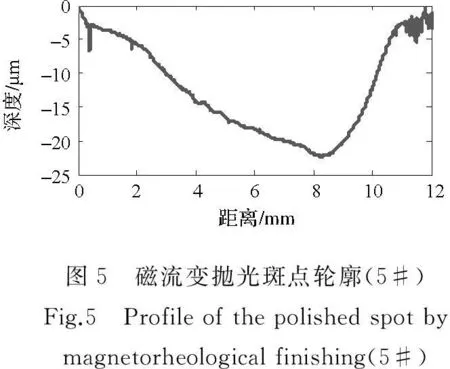
下面以某一组参数的损伤深度检测为例进行说明。图5展示5#抛光斑点中线的轮廓形貌，图6给出了5#抛光斑点中离起点不同距离处的表面缺陷显微图像。根据图6显示，当距离达到5.44mm时表面的缺陷消失，结合图5所示的轮廓曲线可知此处的深度为17.23μm，因此把该深度值作为采用5#参数时造成的亚表面损伤深度。

采用同样的方法可以获得其余各组参数对应的亚表面损伤深度值，具体数值在表1中列出，将深度值通过图像的形式直观表示出来，结果如图7所示。

从该实验结果可以看出，基于本文选取的磨削试验参数条件下，热压多晶氟化镁试件中心位置亚表面损伤深度值最小，为12.79μm；随着径向位置坐标的增大，损伤深度值逐渐增大到20.96μm。该试验结果与前面的预测模型相吻合。

表1　亚表面损伤深度检测结果

图7　亚表面损伤深度曲线Fig.7　Depths curve of sub-surface damage

3结论

1)结合高陡度非球面小磨头磨削方式的特点，通过理论计算建立了亚表面损伤预测模型，根据模型判断非球面磨削亚表面损伤深度随径向坐标的增大逐渐增大。

2)以热压多晶氟化镁平面试件为对象进行了模拟实验，通过磁流变抛斑点法得到各组参数下亚表面损伤深度情况，损伤深度范围在12.79μm～20.96μm之间，且随试件径向坐标的增大而增大，结果与前面的预测模型相吻合。

参考文献(References)

[1]Mills J P. Conformal optics theory and practice [C]//Proceedings of SPIE,Novel Optical Systems Design and Optimization Ⅳ, 2001.

[2]Schaefer J, Eichholtz R A,Sulzbach F C. Fabrication challenges associated with conformal optics [C]//Proceedings of SPIE,Window and Dome Technologies and Materials Ⅶ, 2001.

[3]李跃龙, 黎建明, 苏小平,等. 红外窗口和整流罩材料研究现状与发展趋势[J]. 人工晶体学报, 2007, 36(4): 877-884.

LI Yuelong, LI Jianmin, SU Xiaoping, et al. Research trends and current status in infrared window and dome materials[J]. Journal of Synthetic Crystals, 2007, 36(4): 877-884. (in Chinese)

[4]周劲松, 吕科, 祝海峰,等. 热压氟化镁红外材料研究与应用进展[J]. 硅酸盐通报, 2010, 29(4): 888-892.

ZHOU Jinsong, LYU Ke,ZHU Haifeng,et al.Research and application progress of hot-pressing magnesium fluoride infrared material[J]. Bulletin of the Chinese Ceramic Society, 2010, 29(4): 888-892. (in Chinese)

[5]戴一帆, 袁征, 陈浩锋,等. 热压多晶氟化镁的磁流变抛光研究[J]. 国防科技大学学报, 2008, 30(5): 99-102.

DAI Yifan, YUAN Zheng,CHEN Haofeng,et al.Magnetorheological finishing for MgF2crystal processed under high temperature and high pressure [J]. Journal of National University of Defense Technology,2008, 30(5): 99-102. (in Chinese)

[6]Inasaki I. Grinding of hard and brittle materials[J]. CIRP Annals-Manufacturing Technology, 1987, 36(2): 463-471.

[7]Bi Zhang, Trevor D H. Subsurface evaluation of ground ceramics[J]. Annals of the CIRP, 1995,44(1): 263-266.

[8]Randi J A, Lambropoulos J C, Jacobs S D. Subsurface damage in some single crystalline optical materials[J]. Applied Optics, 2005, 44(12): 2241-2249.

http://journal.nudt.edu.cn

Subsurface damage rule of deep aspheric surface by grinding

ZHUDengchao1,2,DAIYifan1,2,GUANChaoliang1,2,WANGGuilin1,2

(1. College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China;

2. Hunan Key Laboratory of Ultra-precision Machining Technology, Changsha 410073, China)

Abstract：Deep aspheric optical element can obviously improve the aerodynamic performance of the optical system, thus enhancing and optimizing the comprehensive performance of optical system. The grinding method can be used for primary machining of such elements. However, subsurface damage will be inevitably introduced by this method, and grinding parameters will be changing in real time in the processing of deep aspheric surface, so the depths of subsurface damage of the workpiece are inconsistent. In view of this situation, subsurface damage prediction model was established. Combined with the characteristics of semi-sphere wheels grinding, a theoretical calculation was made to predict distributive regularity of the aspheric grinding subsurface damage depths aspheric characteristics. On the basis of the above work, a simulation experiment on hot-pressing polycrystalline magnesium fluoride plane was carried out. Subsurface damage depths under different conditions of grinding parameters were acquired by the method of magnetorheological finishing spot. Results show that the depth range is between 12.79μm and 20.96μm, which increases from inside to outside along the radius of the workpiece and the results are coincide with previous forecast model.

Key words:deep aspheric surface； sub-surface damage； prediction model； hot-pressing polycrystalline magnesium fluoride

中图分类号:TH161

文献标志码：A

文章编号：1001-2486(2015)06-043-05

作者简介：朱登超(1985—)，男，河南新郑人，博士研究生，E-mail：zhudengchao@126.com;戴一帆(通信作者)，男，教授，博士，博士生导师，E-mail：dfy@nudt.edu.cn

基金项目：国家自然科学基金资助项目(51305450)

收稿日期：*2015-07-24

doi:10.11887/j.cn.201506010