纯满同态的推广对条件(P′)与条件(PE)的刻画
2015-02-02乔虎生杨丽丽
乔虎生,杨丽丽
(西北师范大学数学与统计学院,甘肃兰州 730070)
纯满同态的推广对条件(P′)与条件(PE)的刻画
乔虎生,杨丽丽
(西北师范大学数学与统计学院,甘肃兰州730070)
摘要:设S是幺半群,n是一个正整数.设ψ:X→Y是S-满同态,如果ψ是2-纯的,X满足条件(P),那么Y满足条件(P),但反之未必成立.本文给出了纯满同态的一些新推广.利用这些新概念,我们给出了条件(P′)与条件(PE)的等价刻画,即S-系Y满足条件(P′)的充分必要条件是每个满同态X→Y是弱2-纯的,S-系Y满足条件(PE)的充分必要条件是每个满同态X→Y是PE-2-纯的.最后,研究了新满同态的有向上极限.
关键词:纯满同态;条件(P′);条件(PE)
0引言
设S为幺半群,As是单式右S-系.文献[1-6]已经研究了S-系的纯性.
设ψ:X→Y是S-满同态,称ψ为满同态,若对每个有限表示S-系A和每个S-同态f:A→Y,存在g:A→X,使得有以下交换图:
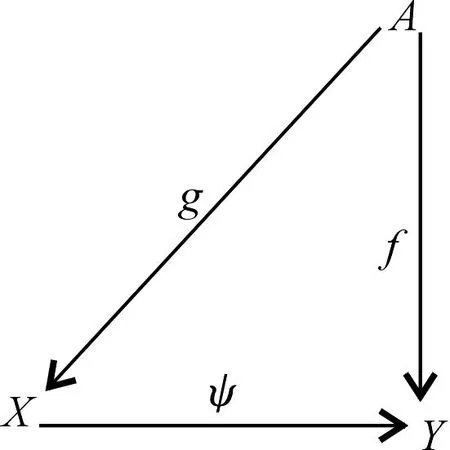
S-系被称作是强平坦的[2],若S-系满足条件(P)与条件(E).称A满足条件(P),若对任意的a,a′∈A,任意的s,s′∈S,若as=a′s′,则存在a″∈A,u,v∈S使得us=vs′,a=a″u,a′=a″v.称A满足条件(E),若对任意的a∈A,任意的s,s′∈S,若as=as′,则存在a′∈A,u∈S使得us=us′,a=a′u.
1987年,Normak[7]证明了右S-系满足条件(E)当且仅当每个满同态ψ:X→Y是1-纯的.满同态ψ:X→Y被称作是1-纯的,若对每个y∈Y和关系ysi=yti,i=1,…,n,存在x∈X,使得对所有的i,有ψ(x)=y与xsi=xti成立.
2012年,Bailey和 Renshaw给出了n-纯满同态的概念,此为纯满同态的扩展.但是他们只利用2-纯满同态给出了满足条件(P)的必要条件.本文给出关于纯满同态概念的一些新的推广,从而得到相应S-系的充分必要条件的刻画,并且证明了这些新的满同态关于有向上极限是封闭的.
1主要结果
定义1[8]称A满足条件(P′),如果对任意的a,a′∈A,任意的s,s′,z∈S,若as=a′s′,sz=s′z,则存在a″∈A,u,v∈S使得us=vs′,a=a″u,a′=a″v.
定义2设ψ:X→Y是满同态.我们称ψ是弱2-纯的,若对任意的y1,y2∈Y,任意的s,t,z∈S,若y1s=y2t,sz=tz,则存在x1,x2∈X使得ψ(x1)=y1,ψ(x2)=y2,并且x1s=x2t.
定理1设S是幺半群,则以下条件等价:
(1)Y满足条件(P′).
(2)设ψ:X→Y是满同态,那么对每个y,y′∈Y,si,ti,z∈S和关系ysi=y′ti,siz=tiz,i=1,…n,存在x1,x2∈X使得对所有的i,有ψ(x1)=y,ψ(x2)=y′并且x1si=x2ti.
(3)每个满同态ψ:X→Y是弱2-纯的.
证明(1)⟹(2).假定ψ:X→Y是满同态,若ysi=y′ti以及siz=tiz,其中i=1,…,n,si,ti,z∈S并且y,y′∈Y.由于Y满足条件(P′),所以对ys1=y′t1和s1z=t1z,存在u1,u1′∈S,y1∈Y,使得y=y1u1,y′=y1u1′并且u1s1=u1′t1.由于y1(u1s2)=y1(u1′t2)并且u1s2z=u1′t2z,所以存在u2,u2′∈S,y2∈Y使得y1u1=y2u2,y1u1′=y2u2′并且u2(u1s2)=u2′(u1t2).通过归纳,存在u,u′∈S,y″∈Y,使得y=y″u,y′=y″u′并且usi=u′ti.由于ψ是满同态,所以存在x′∈X使得ψ(x′)=y″.因此
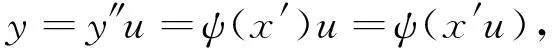
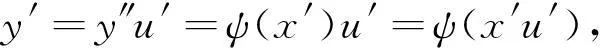
并且很显然有(x′u)si=(x′u′)ti.记
我们可得到结果.
(2)⟹(3)是显然的.
(3)⟹(1).不失一般性,我们选择一个S-系X满足条件(P′),ψ:X→Y是弱2-纯满同态.假定y,y′∈Y,s,t,z∈S,使得ys=y′t,sz=tz.由于ψ是弱2-纯的满同态,所以存在x,x′∈X使得ψ(x)=y,ψ(x′)=y′,xs=x′t.由条件(P′)可知,存在x1∈X,u,u′∈S使得
x=x1u,x′=x1u′,us=u′t.
又因为
所以Y满足条件(P′).】
推论1设S是幺半群,ψ:X→Y是满同态,其中X满足条件(P′),则Y满足条件(P′)的充分必要条件是ψ是弱2-纯的.
定义3[9]设I是拟序集(即I满足自反性与传递性).称S-系集(Xi)i∈I与S-同态集φi,j:Xi→Xj,i≤j∈I所形成的集族(Xi,φi,j)为正向系,若以下两条性质成立:
(1)φi,i=1Xi,i∈I.
(2)φj,k∘φi,j=φi,k,i≤j≤k.
定义4[9]称带有S-同态的αi:Xi→X的S-系X为正向系(Xi,φi,j)的上极限,若以下两条性质成立:
(1)αj∘φi,j=αi,其中i≤j.
(2)设Y是S-系,βi:Xi→Y是S-同态,使得βj∘φi,j=βi,其中i≤j,那么存在唯一的S-同态ψ:X→Y,使得对所有的i∈I,有以下交换图:
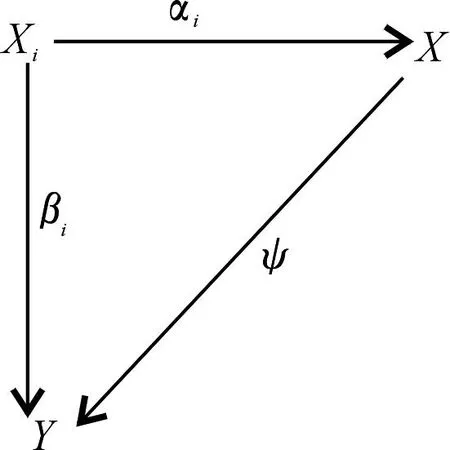
若指标集I满足性质:对所有的i,j∈I,存在k∈I使得k≥i,j,那么称指标集I是有向集.假定指标集I是有向集,则按上述定义可以得到正向系(Xi,φi,j)的有向上极限.
由文献[1],假定(Xi,φi,j)和(Yi,θi,j)是S-系的有向系,且对每个i∈I,存在S-同态ψi:Xi→Xj.进一步,假定(X,βi)和(Y,αi)是有向系的有向上极限,使得对所有的i≤j∈I有以下交换图:
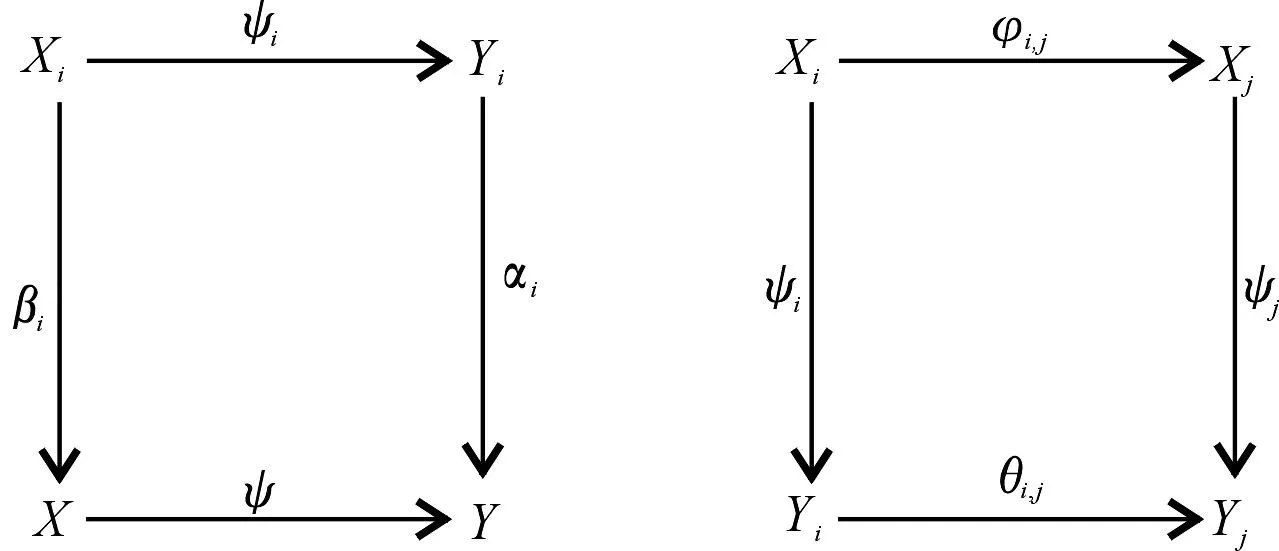
那么称ψ是ψi的有向上极限.
定理2设S是幺半群,弱2-纯S-满同态的有向上极限是弱2-纯的.
证明假定(Xi,φi,j)和(Yi,θi,j)是S-系的有向系,假定对每个i∈I存在着一个弱2-纯S-满同态ψi:Xi→Xj.并且假定(X,βi)和(Y,αi)是正向系的有向上极限,其中αi是满同态,使得对所有的i≤j∈I有以下交换图:
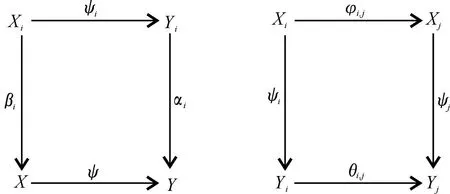
假定ysp=y′tp,spz=tpz,其中p=1,…,n,sp,tp,z∈S,y,y′∈Y,存在i,j∈I,yi∈Yi,yj∈Yj使得αi(yi)=y,αj(yj)=y′,因此有αi(yisp)=αj(yjtp),即有αi(yi)sp=αj(yj)tp.由于I是有向的,由文献[1]的引理3.5知,存在k≥i,j,使得θi,k(yi)sp=θj,k(yj)tp.由于ψk是弱2-纯S-满同态,所以存在x1,x2∈Xk使得ψk(x1)=θi,k(yi),ψk(x2)=θj,k(yj),x1sp=x2tp.最后,y=αi(yi)=αkθi,k(yi)=αkψk(x1)=ψ(βk(x1)),y′=αj(yj)=αkθj,k(yj)=αkψk(x2)=ψ(βk(x2))并且βk(x1)sp=βk(x2)tp.】
定义5[10]称A满足条件(PE),如果对任意的a,a′∈A,任意的s,s′∈S,若as=a′s′,则存在a″∈A,u,v∈S,e,f∈E(S)使得us=vs′,ae=a″ue,a′f=a″vf,es=s,fs′=s′.
定义6设ψ:X→Y是满同态.称ψ是PE-2-纯的,若对任意的y1,y2∈Y,任意的s,t∈S,y1s=y2t,存在x1,x2∈X,e,f∈E(S)使得ψ(x1)e=y1e,ψ(x2)f=y2f并且x1s=x2t,es=s,fs′=s′.
定理3设S是幺半群,Y满足条件(PE)的充分必要条件是每个满同态ψ:X→Y是PE-2-纯的.
证明必要性.假设ψ:X→Y是满同态,并且y1s=y2t,其中y1,y2∈Y,s,t∈S.由于Y满足条件(PE),所以存在u,v∈S,y′∈Y,e,f∈E(S),使得y1e=y′ue,y2f=y′vf,us=vt,es=s,fs′=s′.又因为ψ是满同态,所以存在x′∈X使得ψ(x′)=y′,因此
并且显然有(x′u)s=(x′v)t.记x1=x′u,x2=x′v,则结论成立.
充分性.设X满足条件(PE)且ψ:X→Y是PE-2-纯满同态,假定y1,y2∈Y,s,t∈S使得y1s=y2t,由于ψ是PE-2-纯的,所以存在x1,x2∈X,e,f∈E(S)使得ψ(x1)e=y1e,ψ(x2)f=y2f,x1s=x2t,es=s,fs′=s′.由条件(PE),存在x′∈X,u,v∈S,e,f∈E(S),使得x1e=x′ue,x2f=x′vf,us=vt.又因为y1e=ψ(x1)e=ψ(x′u)e=ψ(x′)ue,y2f=ψ(x2)f=ψ(x′v)f=ψ(x′)vf,并且ψ(x′)∈Y,所以Y满足(PE).】
推论2设S是幺半群,ψ:X→Y是满同态,其中X满足条件(PE),则Y满足条件(PE)的充分必要条件是ψ是PE-2-纯的.
定理4设S是幺半群,PE-2-纯S-满同态的有向上极限是PE-2-纯的.
证明假定(Xi,φi,j)和(Yi,θi,j)是S-系的正向系,假定对每个i∈I存在一个PE-2-纯S-满同态ψi:Xi→Yi,并且假定(X,βi)和(Y,αi)是正向系的有向上极限,其中αi是满同态,使得对所有的i≤j∈I有以下交换图:
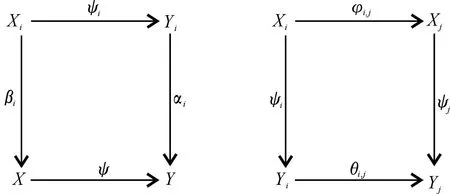
假定ysp=y′tp,其中p=1,…,n,sp,tp∈S,y,y′∈Y,则存在i,j∈I,yi∈Yi,yj∈Yj使得αi(yi)=y,αj(yj)=y′,因此αi(yisp)=αj(yjtp),即有αi(yi)sp=αj(yj)tp.由于I是有向的,所以由文献[1]的引理 3.5知,存在k≥i,j,使得θi,k(yi)sp=θj,k(yj)tp.由于ψk是PE-2-纯S-满同态,所以存在x1,x2∈Xk,e,f∈S使得ψk(x1)e=θi,k(yi)e,ψk(x2)f=θj,k(yj)f,x1s=x2t,es=s,fs′=s′.最后,
并且βk(x1)s=βk(x2)t.】
参考文献:
[1]RENSHAWJ.Extensionandamalgamationinmonoidsandsemigroups[J].Proc London Math Soc,1986,52(3):119-141.
[2]STENSTROMB.Flatnessandlocalizationovermonoids[J].Math Nachr,1971,48(1-6):315-334.
[3]RENSHAWJ.Stabilityandflatnessinactsovermonoids[J].Colloquium Math,2002,92(2):267-293.
[4]BASHIRR.Coversanddirectedcolimits[J].Algebr Represent Theory,2004,9(5):423-430.
[5]AHSANJ,LIUZhong-kui.AHomological Approach to the Theory of Monoids[M].Beijing:SciencePress,2008:45-66.
[6]RENSHAWJ.Extension and Amalgamation in Monoids,Semigroups and Rings[D].Scotland:UniversityofStAndrews,1985.
[7]NORMAKP.Onequalizer-flatandpullback-flatacts[J].Semigroup Forum,1987,36(3):293-313.
[8]GOLCHINA,MOHAMMADZADEHH.Oncondition(P′)[J].Semigroup Forum,2013,86:413-430.
[9]BAILEYA,RENSHAWJ.Coversofactsovermonoidsandpureepimorphisms[J].Proceedings of the Edinburgh Mathematical Society,2014,57(3):589-617.
[10]GOLCHINA,MOHAMMADZADEHH.Onhomologicalclassificationofmonoidsbycondition(PE) of right acts[J].ItalianJournalofPureandAppliedMathematics,2009,25:175-186.
(责任编辑马宇鸿)
Characterizations of condition (P′) and condition (PE)by
generalizationsofpureepimorphisms
QIAO Hu-sheng,YANG Li-li
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,Gansu,China)
Abstract:Let S be a monoid and n a positive integer.Let ψ:X→Y be an S-epimorphism in which X satisfies condition (P),if ψ is 2-pure then Y satisfies condition (P),but the converse is not true.Some new generalizations of pure epimorphisms are given.Using these new concepts,some characterizations of condition (P′) and condition (PE) are obtained,that is,a S-act Y satisfies condition (P′),if and only if every S-epimorphism is weak 2-pure,and a S-act Y satisfies condition (PE),if and only if every S-epimorphism is PE-2-pure.Finally,the directed colimits of these new epimorphisms are investigated.
Key words:pure epimorphism; condition (P′);condition (PE)
中图分类号:O 153.3
文献标志码:A
文章编号:1001-988Ⅹ(2015)02-0001-03
作者简介:乔虎生(1974—),男,甘肃灵台人,教授,博士.主要研究方向为半群理论.E-mail:qiaohs@nwnu.edu.cn
基金项目:国家自然科学基金资助项目(11461060);甘肃省高校基本科研业务费项目
收稿日期:2014-09-13;修改稿收到日期:2015-01-06 2014-04-22;修改稿收到日期:2014-07-22
