高考填空题的解法
2015-02-02李金兴萧山中学浙江杭州311201
●李金兴 (萧山中学 浙江杭州 311201)
高考填空题的解法
●李金兴 (萧山中学 浙江杭州 311201)
填空题的结构往往是在一个命题中去掉某个(些)条件或结论,让考生填补上.填空题题目叙述简洁、答案简明,评分客观、公正、准确.与选择题相比,没有选项可供猜测或根据答案选项获得解题线索,更能考查学生独立思考解决问题的能力.浙江省数学高考从2007年起将选择题由12个减为10个、而将填空题由4个增加到7个.预计2015年起,将继续减少选择题题数而增加填空题的份额.因此如何应对填空题型,是高考复习中的重要环节.
1 知识内容
1.1 从考查目的分析
根据以往高考真题来看,填空题的考查内容大致分为3类:1)立足基础知识考查全面性,对一些相对“次要”而选择题中又没有考到的内容作补充考查,涉及知识如程序框图、三视图、线性规划、概率统计(文科)等——通常这些考题比较简单,属“送分题”;2)立足主干内容考查系统性,对高中数学主干知识的解答题型考查作补充,涉及知识如立体几何、解析几何、函数、数列、三角等——一般这些考题属中等难度;3)立足学生思维能力考查创新性,历年高考总会出现一些题型新颖、立意深远、比较灵活的问题,涉及知识很广(包括平面向量、不等式等)——一般这些考题较难,能起到反映改革趋势、探索命题规律、调节试卷结构的作用.
1.2 从解答过程分析
数学填空题多数是计算型(尤其是推理计算型)和概念(性质)判断型,解答时必须进行切实地计算和合乎逻辑地推演和判断.当然也有一些题目可以用观察、特例、归纳等方式“猜”得答案.由于填空题无需书写过程,因此,解题时务必坚持“正确、迅速、合理”的原则:遵循基本的运算程序、运算规律;在此基础上养成理性思维指导计算的习惯,对于一些新颖有难度的问题,要善于观察问题结构特点,分析其数学背景,从而适当转化问题、选择合理的解题方法;避免生搬硬套公式、定理,切忌“小题大做”.此外,填空题的参考答案一般用最简形式表达,这也要求学生有良好的数学表达能力和化简意识.
2 命题分析
2.1 命题特点分析
从2006~2014年浙江省数学高考填空题统计分析,在填空题中从未考过的内容包括“集合、逻辑、空间向量、理科概率和导数”,很少考的内容包括“直线与圆、复数、推理证明”.理科填空题主要集中在“立体几何、圆锥曲线、排列组合、平面向量、线性规划”等,而文科考题则主要集中在“初等函数、平面向量、不等式、线性规划、概率”等.
2 命题趋势分析
由于影响填空题最终结论的因素很多,因此以往填空题往往“考点少、目标集中”,以此来增加考查的信度和效度.尽管如此,与解答题相比,由于没有过程给分,导致错一步而失全局,容易对考生造成较大的心理压力.针对这种现象,2015年浙江省数学高考填空题考查有细化步骤的趋势,旨在让填空题具有更好的区分度.比如有些填空题一题多空、逐步递进、分步评分;既能更客观准确地考查考生解决问题的不同水平,也能在思路上为解题者提供某些线索,要求考生仔细阅读、观察分析、灵活运用.
2015年浙江省数学高考考试内容有所调整,比如:排列组合、二项式定理、复数、导数等放在选修模块中考查,那么必修内容填空题考查内容势必有相应调整:主干内容的考查会进一步增强,创新题型也会频频亮相.
3 典题剖析
3.1 从知识间联系分析数学本质
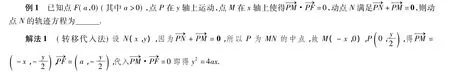
反思由上述步骤可得动点N一定在抛物线y2=4ax上运动,但动点N的轨迹方程是否是y2=4ax还需进一步验证.人教A版教材选修2-1第64页抛物线的形成过程是:设F为定直线l外的定点,在l上任取一点H,过点H作l的垂线与线段FH的垂直平分线交于点M,则点M的轨迹是以F为焦点、l为准线的抛物线.联系教材内容,可得如下解法.
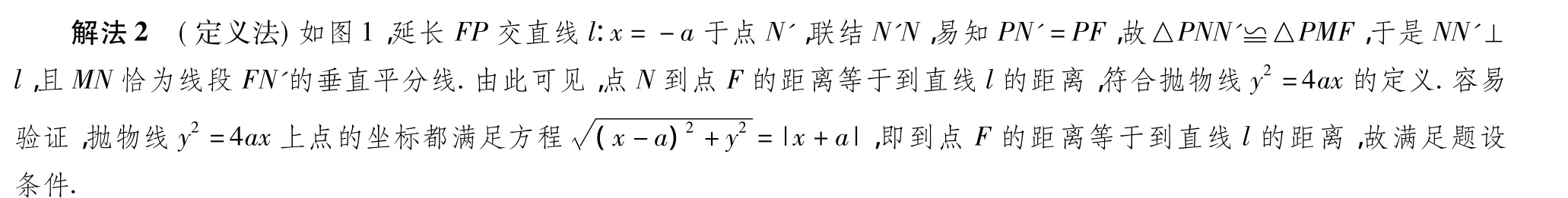
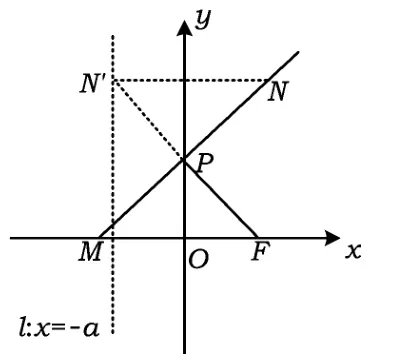
图1
反思动点轨迹恰好是抛物线,那么必定符合抛物线定义,而能用定义去解释轨迹后,才算将它的数学本质揭示出来了.
2.2 从方法比较中领悟适切性
有些问题解法很多,但根据实际情景选择适切的方法需要积累一定的解题经验,而比较分析各种方法的特点能让学生更快地作出正确选择.比如2个向量的数量积有多种算法,教师应引导学生在系列情景中比较、辨别各种算法的优劣,归纳适用范围.


2.3 活用数学思想方法避免小题大做
一些填空题按常规思路,其运算量抵得上一道解答题,此时应该活用数学思想方法简化过程、避免“小题大做”.
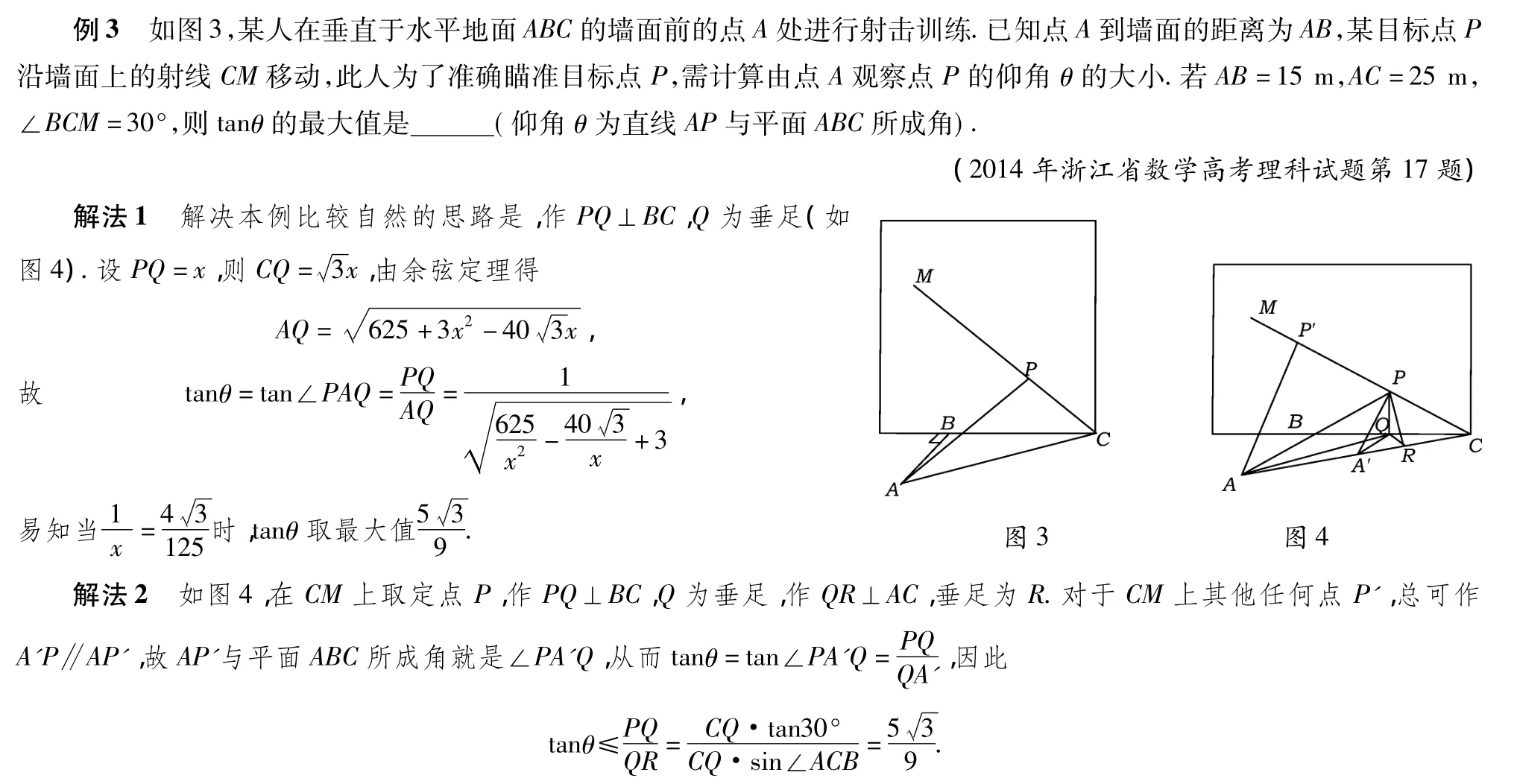
例4已知实数x满足|x|≥2,且x2+ax+b-2=0,则a2+b2的最小值为__ .
解法1按常规思路解读,方程x2+ax+b-2=0有实根x满足|x|≥2,因此可先考虑反面情形——方程x2+ax+b-2=0没有实根,或有2个实根都在(-2,2)内,从而
反思解法2利用“动静转化”的数学思想方法,将点P看作定点、点A看作动点,简化了解题过程,并且清楚地揭示了角θ的最大值恰好等于二面角M-AC-B的平面角.如果用动态的观点看问题,当AP在平面ACM上运动时,所求线面角的最大角即为二面角M-AC-B的大小(二面角的最大角特性).

反思2种解法都用到“数形结合”的思想方法,解法1还用到“正难则反”的解题策略.而解法2采用“变更主元”的策略,将(a,b)看做方程x2+ax+b-2=0的解、x看作系数,从而实现“动静转化”,巧妙地解决了问题.可见,在一些较难的问题解决中,需要将多种数学思想方法组合在一起,才能有效转化问题、快速获得答案.
4 精题集萃


参考答案

