灌溉水库宽浅型优化调度目标函数改进及应用

钟平安,曹明霖,万新宇,尚艳丽

(1. 河海大学水文水资源学院,江苏 南京　210098; 2. 泰安水文水资源勘测局,山东 泰安　271000)



灌溉水库宽浅型优化调度目标函数改进及应用

钟平安1,曹明霖1,万新宇1,尚艳丽2

(1. 河海大学水文水资源学院,江苏 南京210098; 2. 泰安水文水资源勘测局,山东 泰安271000)

摘要：对于灌溉水量时程分配问题,由于需水过程不均匀且时程关联性较强,采用宽浅型优化调度模型解决更加合理。根据宽浅型目标的含义,解析分析了缺水率平方和最小的目标函数。结果表明,该目标函数并不能得到缺水率均匀的供水过程,缺水率与需水量成正比;借鉴缺水率平方和最小目标函数的基本形式,考虑水量平衡约束，构建拉格朗日函数,导出了能得到缺水率均匀的新目标函数;考虑到农作物不同生育期的缺水敏感性不同,引入水分敏感系数，构建了加权缺水率均匀目标函数。通过多种来水过程的实例分析,验证了改进目标函数的合理性和有效性。

关键词：灌溉水库;宽浅型优化调度;目标函数;拉格朗日辅助函数

在灌区总灌溉水量不足的情况下,将有限的水量在农作物各生长阶段进行合理分配,对作物的最终产量会产生巨大的影响。目前常用时间水分生产函数[1-3]来描述作物产量与灌溉水量之间的关系,该函数为非充分灌溉下合理分配供水提供了重要的理论依据。但对于大范围的灌溉系统,例如区域水资源配置中的农业供水过程分配,往往无法确定准确的分时段水分生产函数。在大范围灌溉水库的优化调度中,多数是借鉴水分生产函数的原理,假定灌溉供水量与农作物产量成正相关,采用供水量最大[4]或缺水量最小替代农作物产量最大作为灌溉水量分配的目标函数。

以缺水量最小为目标的供水调度方式一般可以分为两类:第一类,以保障需水为前提,有水就供,有余水就蓄,蓄满后弃水,其特点是不考虑需水在时间上的相关性,在供水量不足时缺水量(率)主要集中在调度期的后期,缺水持续时间短,但缺水深度大,本文简称为窄深型[5-6]调度方式;第二类,充分利用蓄水工程的时程调节能力,在供水量不足时实现各个时段缺水量(率)尽可能均匀,缺水持续时间较长,但缺水深度小,本文简称为宽浅型[7-11]调度方式。宽浅型调度方式对于农业灌溉具有重要意义,因为农作物的各生长阶段之间具有很强的关联性,当供水不足时,分散少量缺水比集中深度缺水的损失要小。现有文献中,采用的宽浅型优化调度目标函数,基本都没有考虑农作物不同生长阶段对水分不足的敏感性差异。

本文首先评估常用的宽浅型优化调度目标函数的优缺点;然后对“时段缺水率平方和最小”目标函数进行改进;再引入水分敏感系数,构造考虑作物水分敏感期的宽浅型调度的新目标函数;最后,进行了实证分析,佐证本文提出目标函数的合理性。

1宽浅型优化调度数学模型

1.1　目标函数

目前,常见有两种宽浅型优化调度目标,一种是绝对缺水量均匀,即各时段绝对缺水量尽可能均匀[12],其目标函数如式(1)所示;另一种是各时段相对缺水量(缺水率)均匀[13],其目标函数如式(2)所示。

(1)

(2)

式中:G(t)——水库t时段的供水量,为决策变量;X(t)——t时段的总需水量;m——调度期时段数。

当需水量时程分配比较均匀时,采用式(1)作为目标函数相对比较简单。由于农作物各生长阶段之间具有很强的关联性,任何生长阶段的集中缺水都可能使农作物减产，甚至绝收。式(1)虽然能够得到时程上相对均匀的绝对缺水量,但会导致各时段相对缺水量(缺水率)相差悬殊。对于灌溉水库采用式(2)更合理。因此,笔者主要以式(2)为对象,进行分析与改进。

1.2　约束条件

在水库供水调度过程中,常见的主要约束条件[14-17]有:

水量平衡约束:

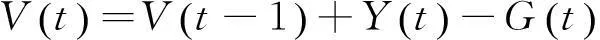
(3)

供水能力及需水量约束:

(4)

蓄水量上下限约束:

(5)

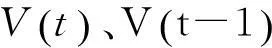
2宽浅型目标函数分析

2.1　关于相对缺水率目标函数

现有文献认为,式(2)能够得到相对缺水率均匀的水库供水过程,有些研究人员甚至基于这一认识,采用需水过程缩放直接求解优化调度模型。实际上,即使在宽松的约束条件之下,式(2)得到的最优解也不是各时段相对缺水率均匀的最优解。

设调度期初水库蓄水量为Vo,调度期末水库蓄水量为Ve,根据式(3)的水量平衡方程,在无弃水(只考虑来水较枯的无弃水情形)的情况下,全调度期的水量平衡如下:

(6)

由式(2)和式(6)构造拉格朗日函数:

(7)

根据最优性必要条件,得到方程组如下:

(8)

求解方程组(8)得到时段缺水率为

(9)

由式(9)可知,即使在只考虑水量平衡约束的简单情形之下,各时段的缺水率并不相等,而是与时段需水量X(t)成正比,但X(t)不均匀程度很高时(农业用水通常是这样),高需水时段的绝对缺水量可能会很大,对于农业灌溉而言,关键时段缺水量较大可能产生不利后果。

2.2　相对缺水率均匀目标函数的推导

式(2)可以变形为

(10)

引入临时变量At,构建新的目标函数如下:

(11)

对式(11)构造拉格朗日辅助函数:

(12)

根据最优性必要条件,推求其解析最优解,得到时段缺水率:

(13)

当各时段缺水率均匀,即有

(14)

由式(13)和式(14)可以得到如下等式:

(15)

式(15)两边对时段求和,可得如下等式:

(16)

式(16)左侧为1,于是可以得到

(17)

将式(17)代入式(15)可得

(18)

对比式(18)左右,可以得到

(19)

将式(19)代入式(13)可以得到:

(20)

(21)

2.3　相对缺水率均匀目标函数的改进

农作物不同生长阶段对缺水状况的敏感性程度是不一致的,当发生缺水情况时,应优先保证缺水最敏感时期的供水。诸多学者对作物不同生育期的水分敏感性展开了研究,目前主要通过构造Jensen模型[18-19]模拟农作物生长期内的水分亏缺对产量的影响,从而计算不同生育期作物的水分敏感系数。笔者引入该敏感系数来衡量作物在不同时期对

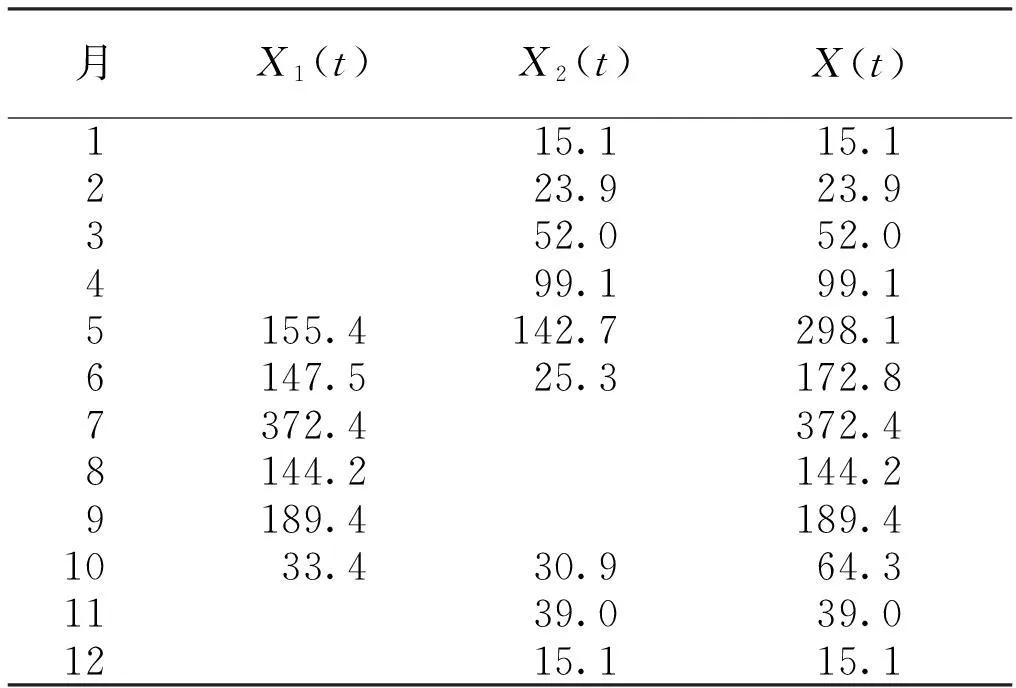
表1　农作物需水过程Table 1　Process of water demand　104 m3

(22)

式中:K(t)——不同生育期作物的水分敏感系数,K(t)值越大,表示该作物t生育阶段水分亏缺对最终产量的影响越大,即在相同的相对缺水量条件下造成的减产损失越大。

3应 用 实 例

3.1　计算条件

某水库为年调节灌溉供水水库,兴利库容为300万m3,死库容为200万m3;设调度期为1 a,以月为计算时段长;调度期始、末蓄水量均为300万m3;月供水能力为500万m3。该灌区种植单季晚稻以及冬小麦2种作物,需水过程如表1所示。

按文献[20]确定2种作物的水分敏感系数，如表2所示。

选择95%、75%这2个频率的典型来水过程Y(1)(t)、Y(2)(t)(表3)生成相应的调度方案,分别记为方案1和方案2。

表2　农作物逐时段水分敏感系数Table 2　Sensitivity coefficients of crop in different growth stages

为2种作物综合的水分敏感系数,以各农作物的需水与总需水的比值为权重,对K1(t)、K2(t)加权平均得到。

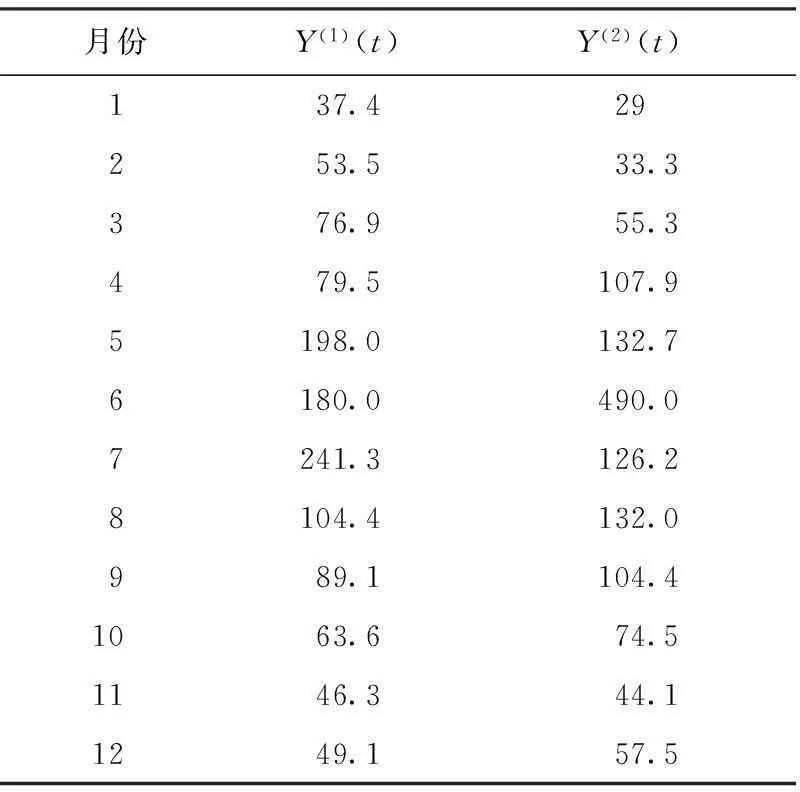
表3　不同方案来水过程Table 3　Inflow processes of different scenarios　104 m3

3.2　结果分析

采用动态规划法计算2种不同来水条件下的优化方案,结果见表4。

表4　不同来水条件下优化调度方案Table 4　Optimal operation schemes with different inflow processes

依据表2和表4,绘制缺水率与综合水分敏感系数关系图，如图1所示。

由表4和图1可知:

a. 在不同来水条件下,式(2)所得各时段缺水率均不一致,需水量越大,缺水率越大;式(21)能够得到时段缺水率均匀的调度方案。式(21)取代式(2)作为各时段缺水率均匀的目标函数是合理的。

b. 由表4可见,式(22)在式(21)基础上考虑了作物在不同生育期的水分敏感性,水分敏感系数K(t)可以使作物的重要生长期得到更多的供水量。

c. 由图1可知,在不同来水条件下,K(t)越大,作物缺水率越小。作物在8月份的水分敏感系数最大,此时对应的时段缺水率较小;11月份的水分敏感系数最小,此时对应的时段缺水率较大。

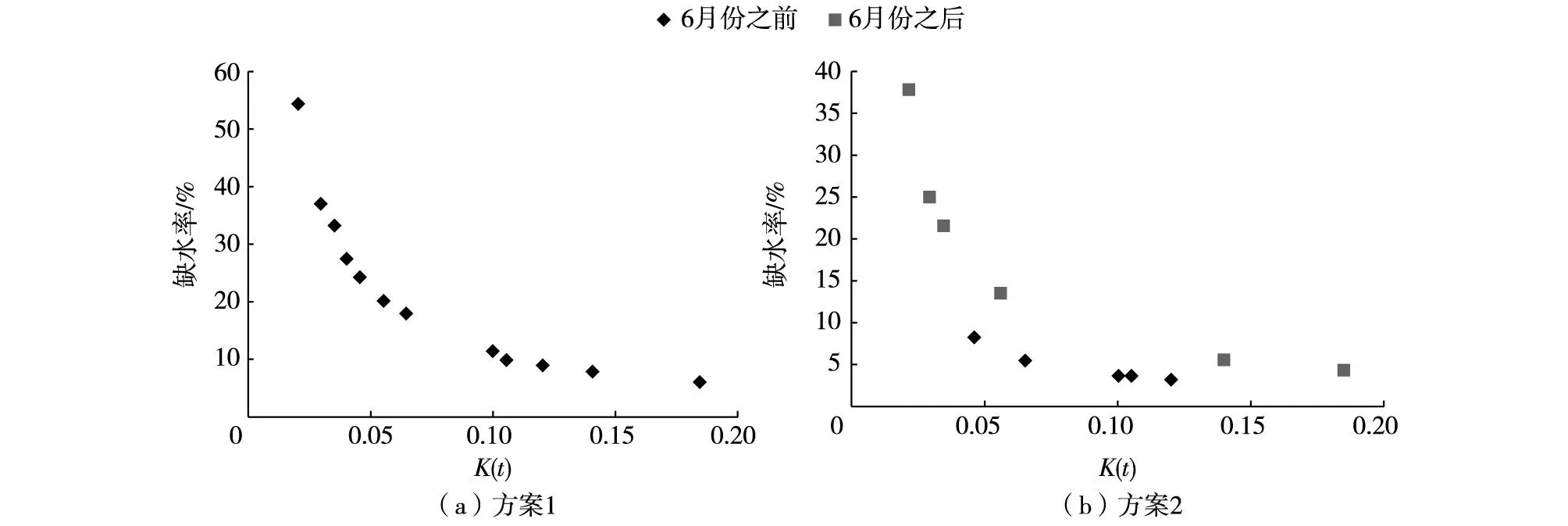
图1　缺水率与综合水分敏感系数关系Fig. 1　Relationships between water deficit ratio and integrated water sensitivity coefficient

d. 由于方案2对应的来水在6月份较丰,为了充分利用来水,防止弃水现象发生,6月份之前应该尽可能利用来水以及水库的蓄水。由表4可知,水库在6月初已到达死库容,说明此前水库已经最大程度的供给灌溉需水。6月份在灌溉需水完全满足且月末蓄水量到达上限的情况下仍然存在余水,故水库在该月存在弃水,弃水量为17.2万m3。由图1(b)可知,方案2以6月份为界将调度期分为2段,均存在K(t)越大,作物缺水率越小的关系。

由上可见,式(22)作为改进的宽浅型优化调度目标函数合理有效。

4结语

对于以农业灌溉为主的供水时程分配问题,由于需水过程不均匀且时程关联性较强,采用宽浅型优化调度模型解决更为合理。笔者根据宽浅型目标的定义,对缺水率平方和最小目标函数在仅考虑水量平衡约束的前提下进行解析分析,结果表明该目标函数不能得到缺水率均匀的供水过程;借鉴缺水率平方和最小目标函数的基本形式,导出了能得到缺水率均匀的供水过程的新目标函数;考虑到农作物不同生育期对水分不足的敏感程度也不一样,引入水分敏感系数，得到改进的宽浅型目标函数。多种来水过程的实例分析表明,本文提出的改进目标函数合理有效。

参考文献：

[1] 陈亚新,康绍忠. 非充分灌溉原理[M]. 北京:水利电力出版社,1995.

[2] 王莹,彭世彰,王龙,等. 月灌溉用水量分布式优化模型[J]. 排灌机械工程学报,2015,33(2):158-162. (WANG Ying, PENG Shizhang, WANG Long, et al. Distributed monthly irrigation optimization model[J]. Journal of Drainage and Irrigation Machinery Engineering(JDIME), 2015,33(2):158-162. (in Chinese))

[3] CAKR R, CEB U. Yield, water use and yield response factor of flue-cured tobacco under different levels of water supply at various growth stages[J]. Irrigation and Drainage, 2010, 59(4): 453-464.

[4] HAIMES Y Y. Hierarchical analysis of water resources system[M]. New York:McGraw-Hill,1977.

[5] GOODARZI E, ZIAEI M, SHOKRI N. Reservoir operation management by optimization and stochastic simulation[J]. Journal of Water Supply: Research and Technology—AQUA, 2013,62(3):138.

[6] 周惠成,刘莎,程爱民,等. 跨流域引水期间受水水库引水与供水联合调度研究[J].水利学报,2013,44(8):883-891. (ZHOU Huicheng, LIU Sha, CHENG Aimin, et al. Joint operation of water transfer-supply for the reservoir in intake area during inter-basin water transfer[J]. Journal of Hydraulic Engineering,2013,44(8):883-891. (in chinese))

[7] NEELAKANTAN T R, PUNDARIKANTHAN N V. Hedging rule optimization for water supply reservoirs system[J]. Water Resources Management, 1999,13(6):409-426.

[8] TU M, HSU N, TSAI F T C, et al. Optimization of hedging rules for reservoir operations[J]. Journal of Water Resources Planning and Management, 2008,134(1):3-13.

[9] 侍翰生,程吉林,方红远,等. 基于动态规划与模拟退火算法的河—湖—梯级泵站系统水资源优化配置研究[J].水利学报,2013,44(1):91-96. (SHI Hansheng, CHENG Jilin, FANG Hongyuan, et al. Research on optimal water resource allocation of river-lake-pumping stations system by dynamic programming and simulated annealing approach[J]. Journal of Hydraulic Engineering,2013,44(1):91-96.(in Chinese))

[10] YOU G J Y. Hedging rules for the operation of lake okeechobee in Southern Florida[J]. JAWRA Journal of the American Water Resources Association, 2013,49(5):1179-1197.

[11] SHIAU J T. Analytical optimal hedging with explicit incorporation of reservoir release and carryover storage targets[J]. Water Resources Research, 2011,47(1):W01515.

[12] CANCELLIERE A, GIULIANO G, ANCARANI A, et al. A neural networks approach for deriving irrigation reservoir operating rules [J]. Water Resources Management, 2002, 16 (1): 71-88.

[13] 曾祥,胡铁松,郭旭宁,等. 跨流域供水水库群调水启动标准研究[J].水利学报,2013,44(3):253-261. (ZENG Xiang, HU Tiesong, GUO Xuning, et al. Triggering mechanism for inter-basin water transfer-supply in multi-reservoir system[J]. Journal of Hydraulic Engineering, 2013,44(3):253-261. (in Chinese))

[14] 韩义超,徐炜,张弛,等. 径流贝叶斯概率预报在水库发电优化调度中的应用[J]. 水利水电科技进展,2014,34(4):39-45. (HAN Yichao, XU Wei, ZHANG Chi, et al. Building optimization model for reservoir hydropower generation using Bayesian forecasting system and stochastic dynamic programming[J]. Advances in Science and Technology of Water Resources,2014,34(4):39-45.(in Chinese))

[15] 王建群,贾洋洋,肖庆元. 狼群算法在水电站水库优化调度中的应用[J]. 水利水电科技进展,2015,35(3):1-4. (WANG Jianqun, JIA Yangyang, XIAO Qingyuan. Application of wolf pack search algorithm to optimal operation of hydropower station [J]. Advances in Science and Technology of Water Resources, 2015,35(3):1-4.(in Chinese))

[16] 张松达,夏国团,劳冀韵,等. 基于智能算法的水库群联合调度图优化[J]. 水利水电科技进展,2013,33(S1):5-6. (ZHANG Songda, XIA Guotuan, LAO Jiyun, et al. Optimal operation of joint operating rule curves in multi-reservoir system based on intelligent algorithm [J]. Advances in Science and Technology of Water Resources, 2013,33(S1):5-6. (in Chinese))

[17] 刘烨,钟平安,郭乐,等. 基于多重迭代算法的梯级水库群调度图优化方法[J]. 水利水电科技进展,2015,35(1):85-88. (LIU Ye, ZHONG Pingan, GUO Le, et al. Operation chart optimization method of cascade reservoirs based on multiple iteration algorithm[J]. Advances in Science and Technology of Water Resources, 2015,35(1):85-88. (in Chinese))

[18] 缴锡云,雷志栋. 非充分灌溉制度对Jensen模型的敏感性分析[J]. 灌溉排水学报, 2005(2):10-12. (JIAO Xiyun, LEI Zhidong. Sensitivity analysis of deficit irrigation for Jensen’s model[J]. Journal of Irrigation and Drainage, 2005(2):10-12.(in Chinese))

[19] 程卫国,卢文喜,安永凯. 吉林省水稻水分生产函数模型的适应性研究[J]. 灌溉排水学报, 2015(2):61-66. (CHENG Weiguo, LU Wenxi, AN Yongkai. Adaptability of water production function models for rice in jilin province[J]. Journal of Hydraulic Engineering, 2015(2):61-66.(in Chinese))

[20] 许莹,马晓群,田晓飞,等. 安徽省冬小麦和一季稻分时段水分敏感性研究[J]. 中国农学通报, 2011(24):33-39. (XU Ying, MA Xiaoqun, TIAN Xiaofei, et al. Study on water sensitivity of winter wheat and single-season rice in divided period in anhui province[J]. Chinese Agricultural Science Bulletin, 2011(24):33-39.(in Chinese))

Improvement and application of objective function of irrigation reservoir

optimal operation model based on even-shortage water supply hedging rules

ZHONG Pingan1, CAO Minglin1, WAN Xinyu1, SHANG Yanli2

(1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China;

2.HydrologyandWaterResourcesSurveyBureauofTaian,Taian271000,China)

Abstract:An optimal operation model based on the even-shortage water supply hedging rules can be used to solve the time-history allocation problem in irrigation water quantity because the water demand process is uneven and highly correlated with time-histories. The objective function of the minimum square sum of the water deficit ratio was analyzed based on the meaning of an even-shortage water supply object. The results show that the objective function cannot obtain a water supply process with an even water deficit ratio, and the water deficit ratio is proportional to water demand. Based on the fundamental form of the objective function of the minimum square sum of the water deficit ratio, and considering the constraint of the water balance, the Lagrangian function was built and a new objective function with an even water deficit ratio was derived. Considering the sensitivity extent of crops in different growth stages, the weighting objective function with an even water deficit ratio was constructed by introducing the water sensitivity coefficient. The improved objective function was validated by analyzing a variety of water process examples.

Key words:irrigation reservoir; even-shortage water supply hedging rules; objective function; Lagrange auxiliary function

中图分类号：S274.1

文献标志码：A

文章编号：1000-1980(2015)06-0511-07

作者简介：钟平安(1962—)，男，安徽无为人，教授，博士，主要从事水资源规划与管理研究。E-mail:pazhong@hhu.edu.cn

基金项目：“十二五”国家科技支撑计划(2012BAB03B03)；国家自然科学基金(51179044，51379055)；水利部公益性行业科研专项(201501007)

收稿日期：2015-05-12

DOI：10.3876/j.issn.1000-1980.2015.06.002