论实现学校与犯罪分离的空间性分析
2015-01-31丽贝卡·K·穆雷马克·L·斯瓦特谷丰
丽贝卡·K·穆雷 马克·L·斯瓦特 谷丰
内容摘要:虽然有关校园犯罪的文学作品层出不穷,但有关校园犯罪的实证研究却出奇的少。其实,学校和其他社会机构一样,如果缺乏监管就有可能造成年轻人过分积聚,进而引发犯罪。上学和放学的过程就是有关犯罪的高发期。某些相关研究已经证明,校园周边是犯罪的高发地带。但以学校类型、时间和空间为视角对于犯罪格局的研究却少之又少。笔者从时间和空间两方面着手,研究不同类型的学校(公办或者私立)、不同的年级(小学、初级中学、高级中学)犯罪发生可能性的不同。笔者通过采取空间建模(即本体空间范围内的指数性扩展)的方法对上述问题进行了一定的研究。
结果表明,不同的学校有着截然不同的犯罪格局,这也就意味着对于学校类型进行区分对于了解犯罪的空间格局是十分必要的
关键词:学校与犯罪;空间分析;日常行为理论
尽管学校是社会进步最重要的标志之一,但它有时也可能是一个十分危险的地方。根据2006年青少年犯罪预防年度报告的数据统计:仅在这一年中,在校园内部或学校周围,平均每1000儿童中就会发生大约35起暴力事件、45起盗窃事件。 几次备受瞩目的事件已经引起了社会对于学校在导致青少年犯罪与受害方面的责任问题的广泛关注。因此,大量学者对于校园犯罪的起因和结果问题展开研究。研究人员指出,就校园犯罪而言,无论在个人层面 或是学校层面 都存在一定的危险因素。尽管校园犯罪问题已经引起了广泛关注,但对于学校自身对周围街区的影响的研究还十分不足,通过空间分析指出学校作为一个公共机构应当发挥更为重大作用的文章更是凤毛麟角。
我们必须承认的是,学校确实能够很好的反映其所在街区及其周边犯罪情况, 但是除此之外,学校也对其所在街区的犯罪率的高低有重大影响,包括对于潜在犯罪可能性的影响。 学校周围的街区是学生日常上学放学经过的主要地区,也是学生之间以及学生与社会人员交流的频发区,尤其是在放学的时候这种交流更为频发。而且,学校老师和相关人员的安保工作仅限于校园内,对于校园以外的周边街区监管力度不足,这就造成了学生实施非法行为脱离监管的可能性,进而也就造成学生成为犯罪行为实施者和受害者的可能性显著增加。
研究表明,学校周边街区的犯罪率通常居高不下。 不幸的是,很少研究根据学校类型和年级高低的不同对学校对于犯罪情况的影响加以区分,对于学校对周边街区的犯罪情况的影响以实践和空间为象限进行的研究更是少之又少。费尔逊教授2002年提出日常活动理论及有关的先前研究都指出学校对于学生的上学放学的路线选择必须要有科学合理的安排,而且针对不同类型的学校的不同年级时,这种安排应当均有所不同。如果将学校周围的犯罪与这些日常活动联系起来,就会发现随着学校类型与年级高低的不同,周边街区犯罪发生情况有着明显的不同
现有研究希望在先前的研究成果的基础上实现一定的突破,证明学校周边犯罪空间格局远比先前研究所指出的更为错综复杂。因此,找到一种能够分析这些特殊的时间、空间犯罪格局的独特方法是十分必要的。下面我们根据奥马哈市警方2000年至2002年发布的数据,检验学校的类型不同(公办或者私立)以及年级不同(小学、初级中学、高级中学)对于入室盗窃、机动车盗窃、故意伤人三种犯罪行为的空间、时间格局是否有显著影响。
一、文献综述
对于学校和犯罪的调查研究主要分为社会心理学方面、学校本身、街区等方面。 虽然每一个角度对于全面了解学校和犯罪之间的关系都有帮助,但他们都有相当的局限性,即仅仅关注学校与犯罪之间这样一个复杂关系的某一面。
社会心理学方面的研究主要集中于在学校中学生之间的交流是如何导致异常行为的或者犯罪行为的。特别的是,这方面的研究主要关注从人口因素 、家庭因素 、个人因素 的角度去解释一系列学生行为,例如欺凌同学 、暴力行为 以及团伙行为 等等。大多数此类研究认为学校机构层面的因素对于了解学校与犯罪之间的联系有重大意义,因为学校是一个特殊的机构,特殊之处即在于学校中的学生数量是在不断变化的。
从机构角度的研究主要关注在不同的学校机构中学校本身的特色对犯罪率有怎样的影响。 这方面的研究关注的重点在于学校如何管理、学生之间交流的情况以及学校对于暴力犯罪和财产犯罪的影响。 此类研究认为机构层面的风险(例如,人满为患 和学生之间的不平等待遇 等)与学校的高违法犯罪率有密切关系。
从社区团体的角度的研究主要关注学校与更大的社会团体之间复杂的社会动态。 从这个角度出发,学校即是更大社会团体的缩影,也是社区内不法行为和犯罪的摇篮。
大量的研究表明学校周边的犯罪行为和暴力行为通常以发生在校园内作为掩饰。 而且,相关研究表明通过“街道模式”发展的社会化不仅包括社会机构推进的校园文化, 也包括形成校园文化的诸多方式 ,所以即使是遵守学校规章、践行校园守则的个人在周围环境的强烈影响下也会显得十分无力。 由此,学校周边文化的影响力可见一斑。
然而,也有大量的证据证明学校本身对于周围街区有着深远影响。众多年轻人将一天中的大部分时间都花在校园生活上,仅凭这一点就足以证明学校的影响力。虽然此方面的研究受到很大限制。但是已有大量的研究一致证明学校的存在对于周边街区的犯罪布局有着深远的影响。 本项研究主要通过对日常行为理论 及日常行为理论与社会无组织行为 的结合应用来解释在学校周边街区的犯罪中学校所扮演的角色。
奥斯伍德和安德森2004年的研究对于从日常行为理论和社会无组织行为的角度揭示学校对于犯罪的影响起到关键的作用。它揭示了学校层面的家长式教育对学生的种种影响远大于个人对学生的影响。通过线性分等的方法,他们很好地展示了无组织监管对于个人和学校团体作用的不同,并发现团体与团体间的差异远小于相较同一团体内部个体之间的差异。这项研究是十分有价值的,其意义即在于揭示了违法行为不仅仅是由于个人原因所导致的,周围环境的一系列因素也起到举足轻重的作用。这一定论在学校周边发生的违法行为中体现得尤为明显。endprint
尽管在学生群体中个人性格因素 不断变化,进而导致对于长时间的研究来说,个人性格因素缺乏必要的稳定性,但这一领域的研究对于解决实践问题的作用仍尤为突出。同样的,学校因素对于犯罪和暴力行为有着重大的影响 ,尤其在大量的研究已经证实想把学校从周围街区的影响中分离出来是几乎不可能的情况下, 对于此领域的研究更显得十分必要。既然如此,目前的研究应当更为关注对已知环境因素的研究,重点在于对于学校自身确实对犯罪的发生起到了推波助澜的作用这一问题的研究,而不是仅仅关注学校内部可能发生的犯罪问题。日常行为理论是解决这一问题的一个很好的切入点。
科恩和费尔逊于1979年提出暴力型犯罪是潜在肇事者、合适的犯罪目标以及缺乏必要的安保因素在时间和空间上的汇集的结果。费尔逊2002年还在其对自己与科恩对于日常行为理论的重述改编中提出“肇事者希望给其留下印象或者对其表示威吓、支持的旁观者对于预防或者引发犯罪都起到重要的作用,而且肇事者会利用武器、工具或者伪装来避免被他人发现”。由于发现潜在肇事者和合适的犯罪目标对于宏观层面的大量研究来说是十分困难的,所以目前的研究大多关注学校安保工作的进行以及导致犯罪发生可能性提高的因素,包括目击者的存在、伪装以及支持犯罪的群体。
学校之所以成为犯罪的摇篮是由很多因素造成的。在上课期间,学校领导和老师可能仅仅对针对学校财产的犯罪进行重点预防,而对其他方面有所疏忽。由于学生的放学时间比家长下班的时间早几个小时,因此在学校周边的街区中,这个时候的安保情况最为薄弱,进而导致了肇事者有大量的机会去进行盗窃、伤害等很难被侦破的犯罪。费尔逊和奥斯伍德以及他的同事们从犯罪目标、常规和非常规的安保管理以及其他方面入手对犯罪动机进行了深入的分析,并通过这种分析拓展了日常行为理论的适用范围。 奥斯伍德和他的同事们讨论了在所谓的“缺乏核心人物以致无组织汇集”的情况下,将年轻人集中到一起的重要性。这也与大量的青少年犯罪是以集团活动的方式进行的发现相印证。 这解释了缺乏安保的重大影响的同时也说明了将青少年集中从而形成可能的目击者对于预防犯罪的重要作用。最终,伪装在学校周围的犯罪中变得特别常见,原因就在于学生上学或者放学时,总是在固定的时间沿着固定的路线通过学校周围的。换句话说,在上学或者放学时在学校周围出现青年学生并不会引起太多的怀疑,因为他们很可能就是上学或者放学回家而已,而且实际上大部分学生也确实是这样的,并未有犯罪行为发生。
显然,从环境的角度考虑,在学校与犯罪的之间之所以会形成如此错综复杂的关系,是有很多重要的理论因素导致的。在有限的关注学校对于犯罪的预测的研究中上述理论因素也得以印证。最早的几项研究中,隆斯克与罗伯斯科恩1983年在圣地亚哥的研究将学校作为一种非住宅用地,并检测了其对周边环境中的犯罪的影响。他们发现,学校可以很好地预测在学校周边的街区中发生机动车盗窃和抢劫案,特别是对于公立高级中学而言。这一现象仅在那些紧邻学校的街区中尤为明显。对于与学校相隔一个街区以上的街区中,这种作用便消失了。虽然公立高级中学对于紧邻街区有着重大影响,但私立学校即使再大也无法形成这种影响。
隆斯克与法贾尼于1985年在克利夫兰再次进行了隆斯克与罗伯斯科恩1983年的研究,并取得了相近的标志性结果。公立高级中学的存在对于紧邻街区犯罪情况有着积极的影响,但仅限于一个街区的距离之内。在这项研究中,隆斯克与法贾尼强化了对于学校对紧邻街区中非住宅用地的犯罪的影响的研究,结果显示学校作为一种公共设施的特殊地位对于预防犯罪是十分重要的。
2007年,考特和隆斯克在克利夫兰以1990年至2000年间的统计数据为样本研究了学校与盗窃犯罪之间的关系。此项研究意图通过区分公立学校和私立学校以及不同的学校类型(高级中学、初级中学、小学三年级、小学五年级、小学六年级以及小学四到六年级),来进一步明确学校与其周边街区发生的盗窃罪之间的联系。在研究中,他们也把学校周边的街区和学校的学生登记注册程度作为一项独立的变量进行研究。与之前的研究不同,他们发现在包含或者紧邻五年级小学的街区盗窃案发生率较高。
尽管这三项从环境角度出发对于学校与犯罪关系进行研究的项目揭示了学校与犯罪之间空间格局关系日益错综复杂的现状,但他们也不可避免地陷入了两个方法论上的缺陷,特别是没有将空间自始相关作为控制变量以及对于样本学校过多的调查次数。空间相关和空间独立对于从理论方面和统计学方面的研究都起到十分重要的作用。 理论上说,空间上相邻的街区的情况比空间上距离较远的街区更为相似,因此可以说一个区域的犯罪情况很可能影响其周边的其区域,反之亦然。统计数字显示未列入研究的变量也可能在空间上相关,进而造成了在相邻的街区中一个因变量的空间依赖性。由于未考虑到空间自始相关,以上的研究很可能过分强调了学校与其周边街区之间在犯罪问题上的关系。
此外,也有理论提出,青少年在上学时间、周末以及暑假中活动时间空间的变化也对学校周边区域违法犯罪的格局有着重大的影响。由于未考虑到青少年日常活动时间空间的变化,之前的研究很可能低估了学校在犯罪问题上对于其周边街区的影响。
古维斯(罗马)在她2002年的博士毕业论文中对这些问题做了一定的研究。首先,她突出了时空因素的重要性,尽管她认为只是在上课时学校才可能由于其自身原因造成犯罪结果的发生,而不是在上学或者放学的路上。她认识到了适应空间依赖的需要,并恰当地指出,有关于空间本身的关联的问题的研究必须建立在一个极大的实验样本之上。换句话说,创造空间滞后变量的传统方法需要使用的N×N矩阵来观测, 在样本极大的情况下,这种矩阵使用是非常困难的。因此,她采用因素变量法 ,就是将一个或多个独立的变量称之为因素,因素是与原来的因变量相关且与误差项不相关的量。 这些因素被视为因变量的替代,通过替代变量计算在普通最小二乘法模式下因变量的回归值。
因素变量很好地替代了空间滞后因变量并且修正了大型数据集之间空间自始相关性。不幸的是,这种方法在试图解释学校与犯罪之间的复杂关系时会产生一定的问题,因为所选的因素必须与普通最小二乘法的回归值成不相关的趋势。 这对于街区层面的空间数据来说几乎是不可能的,原因就在于在一个区域内发现与犯罪程度相关的非因变量有逻辑上的困难,但是这种逻辑上的困难与相邻区域的犯罪无关。①endprint
由于方法论上的缺陷,先前对于学校与周边街区犯罪空间格局关系的研究,在精确预计学校对于助长其周边区域犯罪风险的程度方面有所欠缺。目前的研究旨在通过在公立/私立层面上,检查学校影响周边街区犯罪的空间和时间格局的情况以及公立/私立学校不同年级学生犯罪的特定动机,来解决这些方法论上的问题。进一步说,这一研究运用皮斯和勒萨2002年提出的矩阵指数空间规格理论来解释空间依赖性,从而避免涉及空间滞后等复杂的因素。
二、方法
(一)数据
本次研究的地址位于内布拉斯加州的奥马哈市,样本为2000年人口普查的数据,以及2000年至2002年犯罪数据。2000年内布拉斯加州的奥马哈市共拥有约379545人,其人口特征使其成为反映美国其他中型城市人口情况的绝佳范例(美国人口普查局,2003年)。②由于还有很多城市人口数量在25万至50万之间,以及其他特大城市,如纽约,芝加哥和洛杉矶(美国人口普查局,2000年),所以相比对于那些特大城市的研究,对奥马哈市情况的研究成果可以更好地推广到其他城市。
先前很多研究均指出以人口普查区域作为分析单位可以很好的评估学校对于犯罪格局的影响程度, 本次研究也将沿用此种方法。即便如此,我们仍必须认识到还有很多局限存在。尽管采取的措施已经尽可能地确保区域的界限可以反映街道的格局,但人口普查区域仍是专门为人口普查信息的收集而设置的单位。还有单位面积不同的问题也会对研究结果产生影响。 当数据从一个个单位汇总时,这种局限就体现出来。并且这种情况极为常见,尤其是在由于设定的任意性导致不同面积的单位被视为同一级别数据的情况下。 我们希望尽量减少这种问题,因为理论上的关系问题研究不应被非理论驱动的因素所影响。
(二)因变量
我们对三个相互区别的因变量做了研究,之所以选择这三个因变量,是因为他们在之前的研究中起到重要作用以及他们与日常行为理论框架的一致性。这三个变量是在奥马哈市警察局2000年至2002年的报告中入室盗窃、机动车盗窃以及故意伤人犯罪的数量。从本次研究的目的来看,商业盗窃和一般的打架斗殴并不在我们研究的范围。尽管很多研究已经证实综合衡量违法犯罪的情况是检测日常行为理论原理的基础, 但是之前将学校作为城市犯罪环境中的犯罪情况较为良好的设施的研究同样证明,在日常行为理论的框架内几种特殊的犯罪最为普遍。 之所以会出现这种情况,是因为犯罪的综合情况的调查不能像侦破个体犯罪情况那样进行位置编码,这就导致了相关的地理位置的研究缺乏准确性。先前很多研究都证实学校对于机动车盗窃案以及入室盗窃案的影响,并指出由于学校安保措施的缺乏,导致在日常上学放学的路上当学生离家较远时,犯罪发生的可能性大大提高。 2004年,斯科特发现大量的入室盗窃案发生在紧邻学校的街区并且与逃学程度紧密相关,这也从侧面证明了学校的存在与青少年犯罪之间的关系。进一步说,这些特殊犯罪往往具有相对较高的侦破率,增加空间研究这些案件的准确性。根据司法统计局2002年公布的数据显示,2000年机动车盗窃案的报案率达到90.4%,入室盗窃案的报案率达到52.4%(其中74.4%都是在非法侵入时报案的),故意伤人案的报案率也达到了58.0%。
总体上说,在2000年至2002年间,奥马哈市警方公布了7,125起入室盗窃案、13,692起机动车盗窃案以及2,690起故意伤人案件。这些案件发生地址的位置编码与泰格街道人口普查使用的地图信息程序精确匹配。③根据日常行为理论的假设,明确这些犯罪的必要性主要与学校的存在有关。正因如此,我们保留每种特殊犯罪的两种特征作为研究样本:第一、包含城市所有街区发生的所有犯罪;第二、发生时间为本年八月至来年五月的周一至周五的上午七点和下午五点(尤其是学生上学、放学或者在学校周围逗留的时间)。
(三)非因变量
主要的非因变量是学校在同一街区或者紧邻街区的存在。虽然这个结果适用于一般学校,但是将不同类型的学校作为同一指标进行测量很可能导致不同类型、不同年级之间的学校的不同被忽略。根据先前的研究以及日常行为理论来看,不同类型学校周边的入室盗窃、机动车盗窃和故意伤人犯罪类型犯罪格局截然不同。从空间地理的角度分析,紧邻不同类型的学校的街区在地理位置上还有一定的重叠。为了此项研究的进行,这些情况我们都将考虑在内。但由于这种情况相对较少(在1,433个街区中有181个街区与多个学校相邻,其中171个街区与不同类型的多个学校相邻),所以我们认为这对于研究结果不会产生实质影响。另外还有8个街区包含了不同类型的学校,对于此我们也将在最后的分析中予以说明。
首先,我们预计公立高级中学所在街区相比其他街区的机动车盗窃案和故意伤人案案发率较高,而且紧邻公立高级中学的街区的入室盗窃案和伤害案案发率也要高于非紧邻公立高级中学的街区。尽管学校范围内的安保工作进行顺利,但高级中学所在街区很可能为机动车盗窃案提供了很大便利,因为在此类街区中有大量无人照看的汽车,并且此类街区还为伤害案件提供了作案对象(上学放学的学生)和工具(从学校或者周围的汽车上取得)。虽然在紧邻学校的街区中机动车盗窃的案发率有所缓和,但在缺乏安保的情况下,伤害案件的案发率仍居高不下。很多同学上学放学时需要穿过学校周围的街区,所以这些区域发生财产性犯罪(例如,入室盗窃)的可能性非常高,原因就在于他们是大量学生的“已知区域”。
第二,我们预计公立初级中学所在街区的故意伤人案案发率较高,而入室盗窃案或机动车盗窃案的案发率相较其他街区不会有太大变化。先前的研究证实相比高级中学,打架斗殴的情况在初级中学更为普遍。 然而,2002年古维斯(罗马)发现发生在高级中学周边街区的犯罪数量相比发生在初级中学周边街区的犯罪数量并没有很大不同。从犯罪整体的宏观角度出发,我们假定潜在犯罪者的数量是一定的。在这样的情况下,我们的假定就可以反映高级中学周边故意伤人案和入室盗窃案的案发情况,前提是在初级中学发生的打架斗殴将导致其故意伤人案的案发率至少与高级中学持平,但是安保工作却能很好地防止学校所在街区入室盗窃案的发生。然而,相比高级中学,初级中学有个明显的特征,即初级中学的学生尚不到可以驾驶的年龄。这一特征大大减少了在那些为机动车盗窃案提供便利的街区的机动车盗窃案的发生数量。我们预计机动车盗窃案同入室盗窃案和故意伤人一样,在紧邻初级中学的街区案发率将显著提升,因为在学校周边接触到机动车的可能性更大。而且,学校周围来来回回的学生也提高了安保的难度,为盗窃案的发生提供了掩护。由于生活在学校周边的人认为初中学生并不到可以驾驶的年龄,并且学生出现在学校周围再正常不过,因此他们就会降低对可疑行为的警惕,进而导致案发率的上升。endprint
第三,我们预计私立学校所在街区及周围街区以上三种犯罪的案发率都不会太高。大部分私立学校规模较小而且是全日制管理,并且私立学校的学生大多来自离学校较远的地方,这减轻了在上学或放学时学生走路回家或在学校周围滞留的情况,也就减少了犯罪威胁的对象,使有限的安保工作(在上学和放学时较短的一段时间内)得以很好地预防犯罪。尽管在私立高中读书的学生大多驾车上学,但由于停车场面积较小,机动车盗窃案发生的可能性也不是很高。
第四,我们预计公立小学所在街区及周围街区以上三种犯罪的案发率都不会太高。尽管小学大多紧邻交通要道,但是大部分学生都是家长开车接送或者乘坐校车到校。上学或放学时大批学校滞留在学校周围无人照看的情况几乎不可能发生。因此小学周围的安保工作通常都足以预防违法犯罪的发生。此外,对于这个年龄层来说,犯罪工具、武器、伪装也数量也相对较少,因为犯罪者很难接触到犯罪对象或在学校周边隐藏自己。
第六,我们预计学校及其周边街区的影响在学期中(本年八月到来年五月)的周一至周五的上午七点和下午五点之间比较显著。根据学校的通常作息,这段时间正好是上学和放学的时间。虽然学校仍然是影响学生校外活动(例如,课余活动、暑期学校等等)的关键因素,但这一时间段确实是学生上学或放学的主要时间。必须指出的是,内布拉斯加州和很多其他州一样,冬天非常寒冷,所以在12月到2月间每月发生的入室盗窃案和机动车盗窃案数量并没有多少变化。但季节间的犯罪率变化却尤为明显,冬季,入室盗窃案的案发率为每月172.67起,机动车盗窃案的案发率为每月325.13起,故意伤人案的案发率为每月44.25起;而其他季节,入室盗窃案的案发率为每月208.75起,机动车盗窃案的案发率为每月407.5起,故意伤人案的案发率为每月72.5起。从数据可以看出,冬季和其他季节的犯罪发生率有显著不同。这些不同必须引起我们的重视,因为事实上在计算其他季节的数据时,我们并未列入夏季(以上三种犯罪案发率最高的季节)的统计数据。
(四)控制变量
经过一系列研究,大量非因变量对于空间犯罪格局的影响已经得到控制。而且大部分影响已经在先前的研究中体现出来,主要包括对于社会组成结构以及社会环境因素的影响。
第一个社会类型变量是街区的居民数量,每一个街区的居民数量的不同决定了其潜在受害人群的数量根本性不同。第二、街区居民人均财产数量表现出其社会经济地位的高低,而社会经济地位的高低与犯罪活动的程度、类型有直接的关系。 本次研究主要通过对非裔美国人和拉美裔美国人的比例情况统计来测定街区的种族组成情况,因为非裔美国人和拉美裔美国人是奥马哈市最大的两个群体。大群体有一个通病,就是犯罪情况相对严重。 我们也对种族异质性变量进行了研究,因为先前的研究表明这一变量比种族变量对于犯罪有更大的影响。 同时,由于65岁以上居民的比例决定该街区提供的安保程度的高低,所以其也作为本次研究的一个重要变量。 最后一个变量是街区内拥有未成年子女的单亲家庭的比例。1986年,史密斯博士发现街区的高犯罪率与此类家庭过分的集中有很大关系。
以上四组变量主要用来控制街区住宅特征的环境影响力。首先,已经有研究证实街区住房的全年空房率与犯罪有明显关系。 第二,街区住房户主自行居住房屋比例也是多重变量研究模型中的一项指标,因为租客的比例明显与犯罪发生的潜在危险程度成正相关态势。 街区内统一住宅中有多位住户的情况比例也是研究的指标之一,因为这一指标与犯罪也有一定联系。 最后过高的人口密度也与犯罪有一定关联并被视为非因变量列入本次研究。
结果
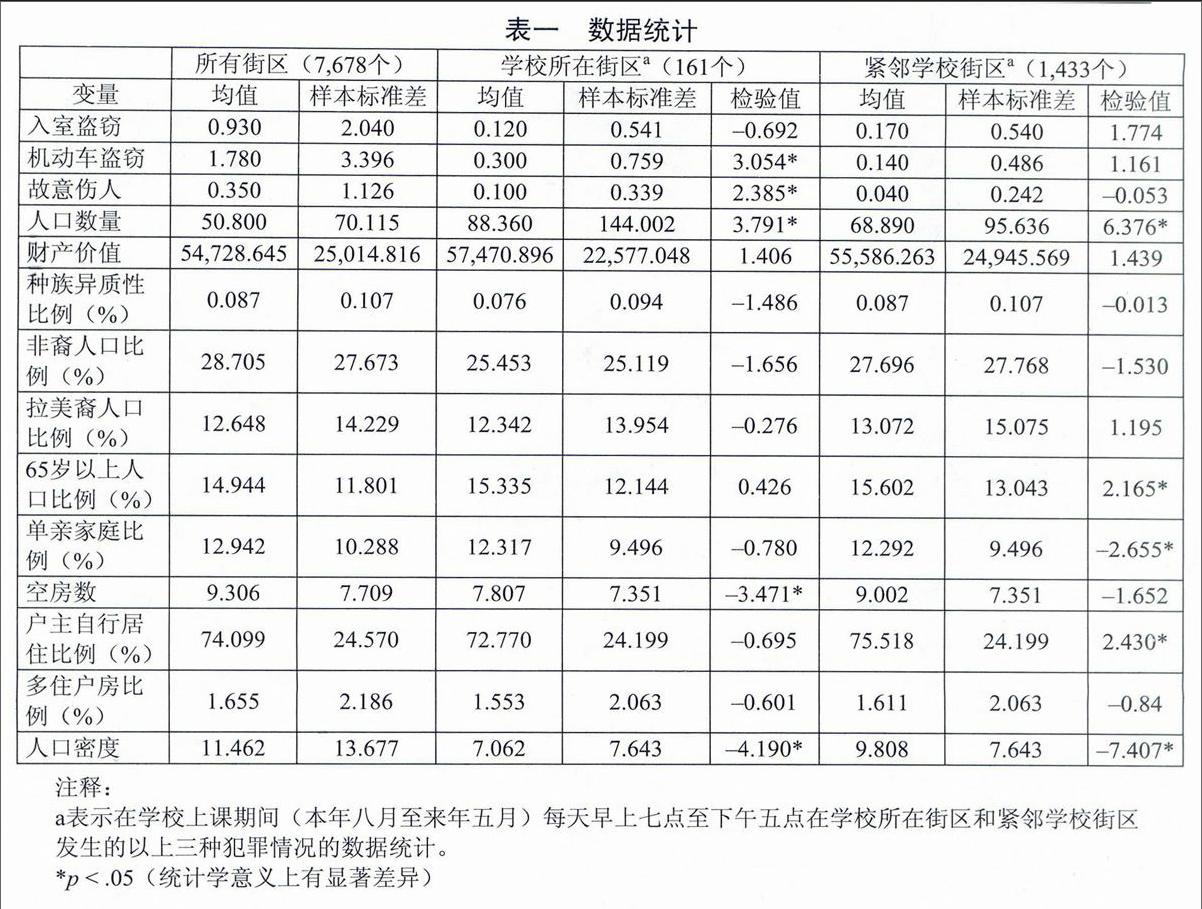
表一 数据统计
所有街区(7,678个) 学校所在街区a(161个) 紧邻学校街区a(1,433个)
变量 均值 样本标准差 均值 样本标准差 检验值 均值 样本标准差 检验值
入室盗窃 0.930 2.040 0.120 0.541 –0.692 0.170 0.540 1.774
机动车盗窃 1.780 3.396 0.300 0.759 3.054* 0.140 0.486 1.161
故意伤人 0.350 1.126 0.100 0.339 2.385* 0.040 0.242 –0.053
人口数量 50.800 70.115 88.360 144.002 3.791* 68.890 95.636 6.376*
财产价值 54,728.645 25,014.816 57,470.896 22,577.048 1.406 55,586.263 24,945.569 1.439
种族异质性比例(%) 0.087 0.107 0.076 0.094 –1.486 0.087 0.107 –0.013
非裔人口比例(%) 28.705 27.673 25.453 25.119 –1.656 27.696 27.768 –1.530
拉美裔人口比例(%) 12.648 14.229 12.342 13.954 –0.276 13.072 15.075 1.195
65岁以上人口比例(%) 14.944 11.801 15.335 12.144 0.426 15.602 13.043 2.165*
单亲家庭比例(%) 12.942 10.288 12.317 9.496 –0.780 12.292 9.496 –2.655*
空房数 9.306 7.709 7.807 7.351 –3.471* 9.002 7.351 –1.652
户主自行居住比例(%) 74.099 24.570 72.770 24.199 –0.695 75.518 24.199 2.430*endprint
多住户房比例(%) 1.655 2.186 1.553 2.063 –0.601 1.611 2.063 –0.84
人口密度 11.462 13.677 7.062 7.643 –4.190* 9.808 7.643 –7.407*
注释:
a表示在学校上课期间(本年八月至来年五月)每天早上七点至下午五点在学校所在街区和紧邻学校街区发生的以上三种犯罪情况的数据统计。
*p < .05(统计学意义上有显著差异)
表一体现了所有街区(学校所在街区、紧邻学校街区、其他街区)变量的统计结果,以及学校所在街区与非学校所在街区、紧邻学校街区与非紧邻学校街区各项变量的对比比较。必须说明的是,所谓非学校所在街区是指本街区内没有学校存在的街区,包含紧邻学校的街区。非紧邻学校街区既排除紧邻学校街区也不包括学校所在街区。在学校所在街区与非学校所在街区的入室盗窃案案发情况几乎相同,但是相比非学校所在街区,学校所在街区在上课时间的机动车盗窃案和故意伤人案的案发率明显较高。除此之外,相比非学校所在街区,学校所在街区通常人口数量较大,空房率较低,人口密度较小。然而,紧邻学校街区入室盗窃案、机动车盗窃案以及故意伤人案的案发情况没有明显增长。事实上,紧邻学校街区的故意伤人案案发率甚至低于其他街区的平均水平,虽然差距也不是特别明显。相比非紧邻学校街区和非学校所在街区,紧邻学校街区通常人口数量较大,65岁以上居民比例较高,单亲家庭比例较低,户主自行居住房屋比例较高,人口密度较小。
尽管不是变量都罗列在表格中,但本次研究确实包含了所有区域相关变量之间的联系。大多数非因变量都与三个变量有着紧密的联系,唯独空房率可能仅与入室盗窃和故意伤人案有紧密联系,与机动车盗窃案联系不是十分紧密。在以上三种犯罪中,变量之间的联系是始终保持的,而且非因变量之间关系的细微变化也印证了变量之间复杂线性关系并不会对本次研究造成困难。⑤
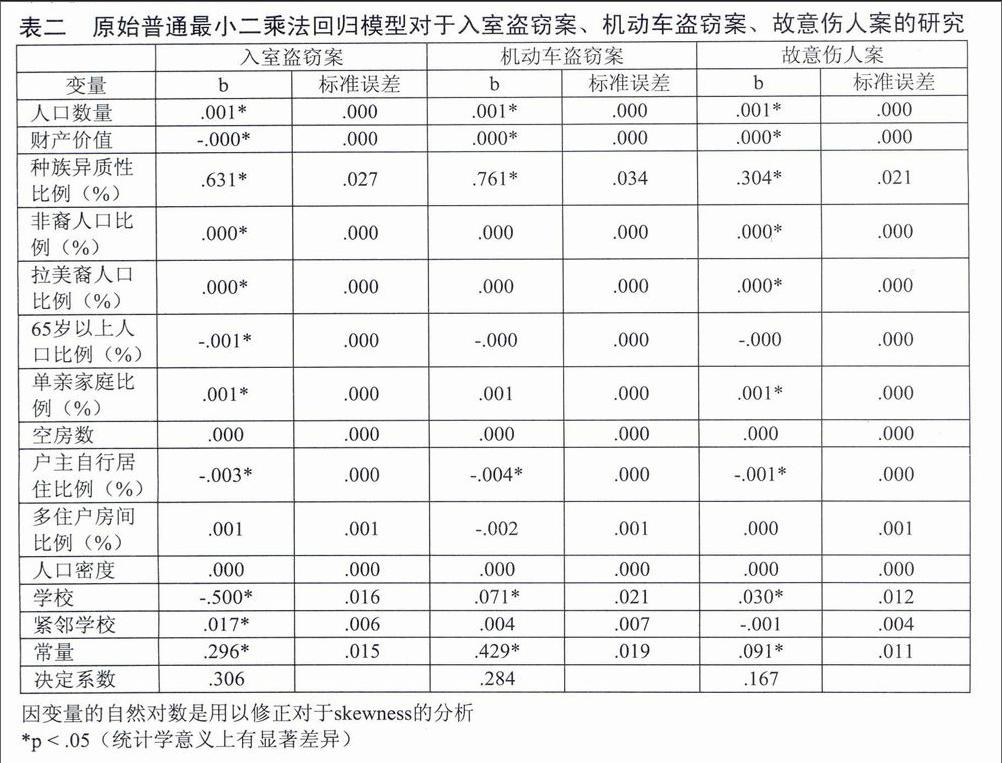
原本的普通最小二乘法模型是用来评估在二元相关体系下引入其他变量后最初的联系是否依然紧密,以及模型的充足率和规范性问题,但是却忽略了空间自始关联性。⑥由于因变量的偏态分布,原始的模型中会有异方差的出现。为解决此问题,每个因变量通过因子的增加以及自然对数的应用进行转化。这种转化在所有模型中均有使用。多元普通最小二乘法回归模型应用于入室盗窃、机动车盗窃和故意伤人案中的统计数据体现在表二中。如表二所示,学校所在街区机动车盗窃案和故意伤人案的案发率明显较高,但是紧邻学校的街区相关情况较为良好。事实上,紧邻学校的街区故意伤人案的案发率甚至低于平均水平,尽管相差程度不是很明显。学校所在街区入室盗窃案的数量明显较少,而且该类案件在紧邻学校街区问题却较为严重。
表二 原始普通最小二乘法回归模型对于入室盗窃案、机动车盗窃案、故意伤人案的研究
入室盗窃案 机动车盗窃案 故意伤人案
变量 b 标准误差 b 标准误差 b 标准误差
人口数量 .001* .000 .001* .000 .001* .000
财产价值 -.000* .000 .000* .000 .000* .000
种族异质性比例(%) .631* .027 .761* .034 .304* .021
非裔人口比例(%) .000* .000 .000 .000 .000* .000
拉美裔人口比例(%) .000* .000 .000 .000 .000* .000
65岁以上人口比例(%) -.001* .000 -.000 .000 -.000 .000
单亲家庭比例(%) .001* .000 .001 .000 .001* .000
空房数 .000 .000 .000 .000 .000 .000
户主自行居住比例(%) -.003* .000 -.004* .000 -.001* .000
多住户房间比例(%) .001 .001 -.002 .001 .000 .001
人口密度 .000 .000 .000 .000 .000 .000
学校 -.500* .016 .071* .021 .030* .012
紧邻学校 .017* .006 .004 .007 -.001 .004
常量 .296* .015 .429* .019 .091* .011
决定系数 .306 .284 .167
因变量的自然对数是用以修正对于skewness的分析
*p < .05(统计学意义上有显著差异)
莫兰的I指标是用来检测一阶空间自始相关的存在。 对于所有的因变量来说,这种统计表明了正向空间自始相关的存在:入室盗窃(I = .034, p < .05),机动车盗窃(I = .024, p < .05),以及故意伤人(I = .053, p < .05)。同样的,皮斯和勒萨2000年发明的矩阵指数空间规格模型也是用来调整多元模型下空间自始相关的存在。
大多数传统的空间滞后模型是通过引入依靠既定加权距离倒数对空间滞后进行预测的因子进行研究的。两阶最小二乘法 的所有观测中都需要使用的N×N矩阵。 1998年,保鲁姆斯汀和科佩尔发现除了计算密集的情况外,大样本可以增加传统计算空间滞后的方法的冗余路径。皮斯和勒萨2000年发明的矩阵指数空间规格模型测量可以很好地替代整个矩阵的矩阵指数的使用。矩阵指数是指作用于类似普通指数函数方阵的矩阵,通常应用于空间研究。这种替代不仅降低了计算时间,而且在计算精度上远远优于其他空间观测方法。 这还创建了一个封闭形式的解决方案,或者一种普适的解决问题的方案,在本次研究中这种方案既指最小平方法。它可以减少冗余路径,同时保持传统空间滞后模型的类似监测参数。endprint
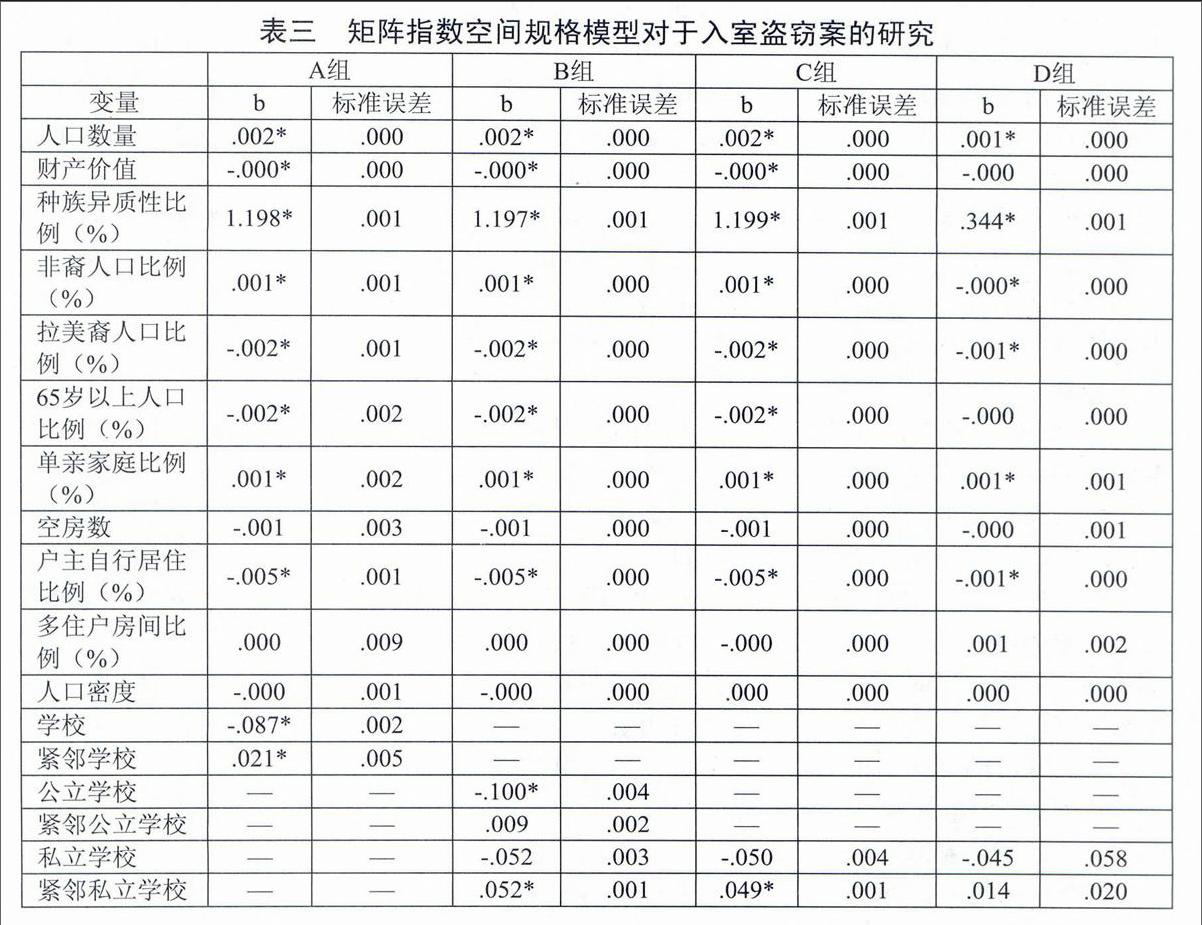
表三 矩阵指数空间规格模型对于入室盗窃案的研究
A组 B组 C组 D组
变量 b 标准误差 b 标准误差 b 标准误差 b 标准误差
人口数量 .002* .000 .002* .000 .002* .000 .001* .000
财产价值 -.000* .000 -.000* .000 -.000* .000 -.000 .000
种族异质性比例(%) 1.198* .001 1.197* .001 1.199* .001 .344* .001
非裔人口比例(%) .001* .001 .001* .000 .001* .000 -.000* .000
拉美裔人口比例(%) -.002* .001 -.002* .000 -.002* .000 -.001* .000
65岁以上人口比例(%) -.002* .002 -.002* .000 -.002* .000 -.000 .000
单亲家庭比例(%) .001* .002 .001* .000 .001* .000 .001* .001
空房数 -.001 .003 -.001 .000 -.001 .000 -.000 .001
户主自行居住比例(%) -.005* .001 -.005* .000 -.005* .000 -.001* .000
多住户房间比例(%) .000 .009 .000 .000 -.000 .000 .001 .002
人口密度 -.000 .001 -.000 .000 .000 .000 .000 .000
学校 -.087* .002 — — — — — —
紧邻学校 .021* .005 — — — — — —
公立学校 — — -.100* .004 — — — —
紧邻公立学校 — — .009 .002 — — — —
私立学校 — — -.052 .003 -.050 .004 -.045 .058
紧邻私立学校 — — .052* .001 .049* .001 .014 .020
高中 — — — — -.169 .010 -.060 .139
紧邻高中 — — — — -.053 .003 .001 .043
初中 — — — — .081 .009 -.023 .128
紧邻初中 — — — — -.034 .003 .005 .036
小学 — — — — -.127* .004 -.052* .052
紧邻小学 — — — — .037* .001 .007 .017
常量 .510* .001 .511* .002 .511* .000 .102* .001
Alpha量 -.325* .000 -.323* .000 -.322* .000 -.116* .000
决定系数 .334 .335 .335 .122
因变量的自然对数是用以修正对于skewness的分析
a D组仅表示在学校上课期间(本年八月至来年五月)每天早上七点至下午五点在学校所在街区和紧邻学校街区发生的犯罪情况的数据统计。
*p < .05(统计学意义上有显著差异)
为了进一步揭示学校与犯罪之间的关系,将学校这一变量分为私立学校和公立学校两个变量。本次模型的结果体现在表三的B组数据中。将学校分为私立学校和公立学校后,公立学校对于入室盗窃案的抑制作用体现得非常明显。与实验预期相比,本次模型得出结论指出,与紧邻公立学校的街区相比,紧邻私立学校的街区入室盗窃案案发率明显较高。这一结论和预期的一致。其他非因变量的系数仍然没有变化。
公立学校变量进一步分为高中、初中、小学,实验数据体现在表三的C组数据中。当将学校按照类型和年级划分之后,很多学校之间的不同立即显现出来。显而易见的是,公立小学对于入室盗窃案的预防效果最为显著。相比其他街区,包含或者紧邻公立高中和初中的街区的入室盗窃案发率相对较低。另外,紧邻小学的街区的案发情况比实验预期情况更为乐观。
表三的D组数据同样按照类型和年级的不同对学校进行了区别研究,但是其将发生在假期内的入室盗窃案排除在研究模型之外。在此情况下,对入室盗窃案有重大影响的是公立小学,其所在的街区的入室盗窃案的数量明显较低。在对上学期间的犯罪时间格局研究方面,本次研究结果与我们的假设一致。
原始矩阵指数空间规格模型对于机动车盗窃案的调查结果显示在表四的A组中。与入室盗窃案的研究模型一样,空间自始相关的修正使模型的方差增加至33.9%。非因变量与机动车盗窃之间的关系并没有太大变化,虽然一旦空间自始相关得以明确,住宅价值对上述关系的影响减轻而人口密度情况则体现出更为重要的影响。在这一模型中,学校所在的街区与紧邻学校的街区的机动车盗窃案案发率情况都不容乐观。
表四中的B组数据显示的是将模型分为公立学校和私立学校而得出调查结果。与实验预期一样,相比私立学校所在街区,公立学校所在街区与紧邻公立学校街区机动车盗窃案的案发率相对较高,尽管这一现象不是特别明显(p = .055)。表四中的C组数据显示的是将公立学校按照学校年级划分而得出的调查结果。和实验预期一样,公立高中所在街区与紧邻公立初中街区的机动车盗窃案案发率较高。与实验预期不同的是,公立初中所在街区的机动车盗窃案案发率也不容乐观。同样,与实验预期相对的,私立学校的机动车盗窃问题最为突出。endprint
表四 矩阵指数空间规格模型对于机动车盗窃案的研究
A组 B组 C组 D组
变量 b 标准误差 b 标准误差 b 标准误差 b 标准误差
人口数量 .003* .001 .003* .000 .003* .000 .001* .000
财产价值 .000 .000 .000 .000 .000 .000 .000 .000
种族异质性比例(%) 1.320* .001 1.317* .001 1.320* .001 .146* .0001
非裔人口比例(%) .000 .001 .000 .000 .000 .000 .000 .000
拉美裔人口比例(%) -.000 .002 -.000 .000 -.000 .000 .000 .000
65岁以上人口比例(%) .000 .003 .000 .000 .000 .000 .000* .000
单亲家庭比例(%) .001 .004 .001 .001 .001 .001 .001* .001
空房数 -.001 .004 -.001 .001 -.001 .001 -.000 .001
户主自行居住比例(%) -.007* .002 -.007* .000 -.007* .000 -.001* .000
多住户房间比例(%) .005 .0216 .005* .002 .005* .002 -.002* .002
人口密度 -.001* .003 -.001 .000 -.001 .000 -.000 .000
学校 .165* .218 — — — — — —
紧邻学校 .033* .075 — — — — — —
公立学校 — — -.184* — — — —
紧邻公立学校 — — .033* — — — —
私立学校 — — .127 .056 .139* .056 .491 .058
紧邻私立学校 — — .029 .020 .033 .020 -.007 .020
高中 — — — — .775* .113 .629* .139
紧邻高中 — — — — .070 .041 .068* .043
初中 — — — — .387* .123 .012 .128
紧邻初中 — — — — .087* .034 .056* .036
小学 — — — — .058 .049 .001 .052
紧邻小学 — — — — .006 .016 -.009 .017
常量 .652* .002 .651* .000 .650* .000 .096* .000
Alpha量 -.440* .000 -.441* .000 -.437* .000 -.177* .000
决定系数 .339 .339 .341 .090
因变量的自然对数是用以修正对于skewness的分析
a D组仅表示在学校上课期间(本年八月至来年五月)每天早上七点至下午五点在学校所在街区和紧邻学校街区发生的犯罪情况的数据统计。
*p < .05(统计学意义上有显著差异)
根据之前对入室盗窃犯罪的观察,将分析对象限制在在学校周围街区学生日常活动时发生的犯罪后,实证结果与我们的假设更为一致(如表四D组数据显示)。另外,公立高中所在街区与紧邻公立高中街区机动车盗窃案案发率较高。最后一次研究结果证明,私立学校与机动车盗窃案的关系和公立初中与机动车盗窃案的关系不是特别明显,这一结果与我们先前的假设不谋而合。然而,值得一提的是,对于案发时间的限制导致单亲家庭比例对于案发情况有明显影响,并且六十五岁以上人口比例越高,在上学或放学时间段内机动车盗窃案的案发率越高。
矩阵指数空间规格模型对于故意伤人案的研究结果体现在表五中。在A组模型中学校类型这一变量并未被分成若干变量。尽管这一变量的空间依赖性是非常明显的。这个模型中的系数相比之前普通最小二分法模型中的结果并没有太大不同。与之前的研究一样,相比其他街区,学校所在街区的故意伤人案案发率明显较高,尽管紧邻学校的街区并不如此。
表五中的B组数据显示的是按照学校类型的不同划分后,运用矩阵指数空间规格模型的研究结果。在这组结果中,仅仅公立学校所在街区的故意伤人案案发率明显较高,也就意味着原来的结果主要是由于此类学校造成。表五中的C组数据显示的是按照学校类型和年级不同划分后,运用矩阵指数空间规格模型的研究结果。在这组结果中,学校与故意伤人案的紧密关系仅仅体现在公立高中所在的街区中。私立高中所在街区、公立初中或小学所在街区以及紧邻任何类型的学校的街区的故意伤人案案发情况均较为良好。
将故意伤人案案发时间限制为上学期间的研究结果体现在表五的D组数据中。这一模型得出的众多结果和先前的研究结果相一致,但是拉美裔居民人口比例对学校与犯罪的关系问题影响不再显著。与先前的研究结果相类似,高中所在街区的故意伤人案案发率相对较高。然而,在这一模型中,公立初中所在街区以及紧邻高中的街区的故意伤人案案发率也相对较高,然而紧邻初中的街区的故意伤人案案发情况良好。
非常有趣的是,在所有分析中,除了人口数,种族异质性和户主自行居住比例是唯一对于所有犯罪影响都十分明显的变量。也就是说,在不同类型的模型中这些变量都保持了相当的稳定性,这对于预测特殊类型的犯罪起到重要作用。
表五 矩阵指数空间规格模型对于故意伤人案的研究endprint
A组 B组 C组 D组
变量 b 标准误差 b 标准误差 b 标准误差 b 标准误差
人口数量 .001* .001 .001* .001 .001* .001 .000* .000
财产价值 -.000* .000 -.000* .000 -.000* .000 -.000* .000
种族异质性比例(%) .558* .001 .557* .001 .560* .001 .091* .0001
非裔人口比例(%) .001* .001 .001* .001 .001* .001 .000* .000
拉美裔人口比例(%) .001* .002 .001* .002 .001* .002 -.000 .000
65岁以上人口比例(%) -.000 .003 -.000 .003 -.000 .003 -.000 .000
单亲家庭比例(%) .003* .004 .003* .004 .003* .004 .001* .000
空房数 -.000 .004 -.000 .004 -.000 .004 .000 .000
户主自行居住比例(%) -.002* .002 -.002* .002 -.002* .002 -.000* .000
多住户房间比例(%) -.000 .016 -.000 .016 -.000 .016 -.001 .000
人口密度 .000 .003 .000 .003 .000 .003 .000 .000
学校 .064* .049 — — — — — —
紧邻学校 .003 .017 — — — — — —
公立学校 — — .087* .037 — — — —
紧邻公立学校 — — .002 .016 — — — —
私立学校 — — .023 .032 .025 .032 .007 .034
紧邻私立学校 — — .001 .011 .001 .011 .007 .012
高中 — — — — .257* .076 .110* .083
紧邻高中 — — — — .027 .024 .037* .026
初中 — — — — .079 .070 .0145* .077
紧邻初中 — — — — -.013 .019 -.010 .021
小学 — — — — .064 .028 .014 .030
紧邻小学 — — — — .001 .009 -.006 .010
常量 .145* .193 .144* .193 .145* .016 .017* .016
Alpha量 -.330* .000 -.333* .000 -.328* .000 -.113* .000
决定系数 .1966 .197 .197 .040
因变量的自然对数是用以修正对于偏度的分析
a D组仅表示在学校上课期间(本年八月至来年五月)每天早上七点至下午五点在学校所在街区和紧邻学校街区发生的犯罪情况的数据统计。
*p < .05(统计学意义上有显著差异)
议题
本次研究调查了学校对周边区域犯罪的影响。日常行为理论认为掌握日常生活中时空的变化对于揭示犯罪活动的格局是十分重要的。由于并未区分学校的年级和类型,先前对于学校和犯罪的研究没能很好地把握这些争议焦点,进而不能充分地控制空间依赖关系的存在,不能很好地限制对于反映学校日常活动的时间维度的分析。我们的分析结论指出如果不考虑以上这些事实要素,研究很可能得出与日常行为理论相悖的结果。正确地面对这些问题后,相应的矛盾情况也会消失。
我们创建了几种关于基于日常行为理论而衍生的学校周边活动格局的特别假说,日常行为理论的基础是安保活动的存在以及犯罪对象、工具、伪装的存在。 必须指出的是,我们认为公立高中所在街区理论上的机动车盗窃案和故意伤人案的案发率应该较高,这一假设在我们最终的分析中得以确认。之后,我们进一步假设紧邻公立高中街区的故意伤人案和入室盗窃案的案发率也应较高。最终,我们发现紧邻高中街区的故意伤人案的案发率的确较高,但入室盗窃的情况较为乐观。
同时,我们认为公立初中所在街区故意伤人案案发率可能较高,在随后的研究中这一假设得以确认。进一步说,我们预计紧邻公立初中街区的机动车盗窃案、入室盗窃案、故意伤人案的案发率均应在较高水平。但我们的分析显示,只有机动车盗窃案在紧邻公立初中的街区案发率较高。相比其他街区,紧邻公立初中的街区在入室盗窃案和故意伤人案案发率方面并没有显著差异。
最后,我们假定私立学校和公立小学所在街区以及紧邻私立学校和公立小学的街区任何犯罪的案发情况均较为乐观。这一假定也确实在我们的分析中得以确认。有趣的是,我们也发现紧邻公立小学街区的入室盗窃案案发率明显较低。尽管这不是本次研究的预期结果,但这与在上学或者放学期间小学附近严格的安保措施密不可分。
本次研究得出几项重要结论如下,第一、我们对于日常行为理论的假设得以实践数据的支持,虽然这些都必须仔细考虑概述如下的局限性。第二,我们也发现很多不一致的结果可以通过对学校的类型和年级进行区分、控制空间依赖性、将分析对象限制在学生在学校周围日常活动的某些时间段等的方式予以解释,这也从侧面证明了方法上的调整对于一项适当的理论研究的重要性。
本次研究仍存在相当的局限性。其中最为严重的是,由于本次研究是以街区为单位的,所以我们并没有考虑学校的大小。另外还有一个重要因素,平均每个公立高中有1,555名学生,而私立高中只有540名学生,仅为公立高中的三分之一。虽然公立小学五年级或六年级的学生人数(平均377人)与私立初中三年级的学生人数(平均340人)相当,但公立初中六到八年级或者七到八年级的学生数量明显较多(平均719人)。这一问题的影响通过将学校视为一个街区的整体并控制该街区的其他变量的方式进行缓解。换句话说,每所学校分别不同的特点不是本次研究的主要范围。
尽管如此,高中学生中潜在肇事者和受害者的庞大规模是本次研究的一大难题。除此之外,本次研究仅调查了一个中西部城市的情况,关于调查结果的分析未必可以推广到其他地区。而且,奥马哈市无论是公立学校还是私立学校都没有体系化的安保措施,而这种体系化的安保措施在其他地区却越来越常见。 还有一个重要的局限是本次研究是建立在官方统计的数据之上的,官方数据很可能低估了犯罪的程度。尽管存在这些限制,但本次研究还是对当前的研究情况作出重要的贡献,主要体现在以下两个方面:
首先,本次研究推进了如何很好地解开学生、学校和街区之间存在的复杂关系的研究进程。本次研究的结果明确指出,仅在学校或者教室范围内检测犯罪情况将掩盖街区与犯罪之间的影响机制。因此几个有关犯罪行为背景的要素就显得尤为关键,包括年龄和犯罪技能水平,犯罪的机会,周围的观众,以及起到控制作用的安保措施的存在。
其次,本次研究提出了有关城市实证研究数据测量的重要问题。特别是,本次研究对相关问题的进一步研究做了理论铺垫并对来自理论框架的变量做了具体的说明。必须声明的是,虽然我们之前的预测很多都得到了证实,但他们仅仅是在本次研究的最终分析中得到证实,而最终分析仅仅排除了空间依赖性、学校类型与年级的不同的影响并将犯罪发生的时间限制在上学期间。随着犯罪学理论的发展,我们也必须通过使用和测试相关理论方法来补充完善我们的研究方法。本次研究仅仅是对青少年犯罪、团体犯罪、犯罪发生的特殊背景等问题的复杂因素的检测的开始,随后我们将继续努力,不断修正和改善我们的研究方法和理论架构。endprint
