基于伪谱法电磁编队六自由度最优控制

陈 晶，岳晓奎

（西北工业大学 陕西 西安 710072）

编队飞行是一项重要的使能技术，基于传统推力器的编队飞行存在推进剂消耗和羽流污染等问题，电磁编队飞行可有效克服上述问题，具有广泛的应用前景[1]。电磁卫星上安有三组正交通电线圈，当配合使用控制力矩陀螺等姿态控制器时，可对卫星的位置和姿态进行协同控制。

之前的相关研究验证了电磁编队飞行的可行性：Kwon[2]研究了电磁卫星近距离时的机动；Eslinger[3]首先在微重力环境下演示验证了电磁卫星。Elias[4]将动力学模型线性化，并采用了非线性控制器。由于系统存在很强的非线性和耦合性，以及众多的约束条件，电磁编队的轨迹重构问题充满挑战。为了生成合理的重构轨迹，先前的研究中分别采用了滑模变结构控制[5]、人工势函数法[6]和最优控制等方法。对于最优控制，伪谱法可用于离散状态空间，其求解方法往往依赖于商业优化软件，如 OTIS和DIDO等。

目前，电磁编队飞行的研究中仍存在一些问题。首先，多数研究往往基于三自由度的动力学模型，这忽略了电磁的耦合特性，因此需建立六自由度的空间相对动力学模型。此外，由于系统存在很强的非线性和耦合性，现有的优化软件有可能并不适用，因此需采用高精度的数值算法进行求解。

文中将首先介绍电磁力学的相关内容，然后推导非线性的姿轨耦合动力学模型，接着利用了勒让德伪谱法，将电磁编队的重构问题转化为有约束的最优控制问题，最后改进数值算法，并进行仿真验证。

1 六自由度动力学模型

在本节，编队的相对轨道动力学模型将描述在固连于主星的Hill系下，相对姿态动力学模型将描述在从星本体系下，坐标系如常规方式定义。

1.1 相对轨道动力学

忽略轨道摄动影响，相对轨道动力学模型可描述为：

其中：

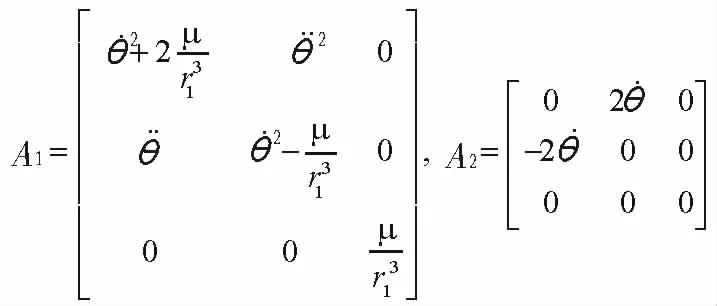
在实际应用中，通常需利用参考轨道的角速度，将该模型进行单位化处理，以提高计算精度。

1.2 相对姿态动力学

对于电磁卫星，切向的电磁力会引起电磁力矩的产生，而由于电磁力矩的幅值有限，通常需在卫星上配置姿态控制系统，本文采用控制力矩陀螺(CMG)模型，将电磁卫星视作六自由度的控制器。对于常规编队的主星，通常任其在空间自由翻滚，对其姿态不加以控制；但电磁编队内的卫星由于受到电磁力矩的作用，需对每颗卫星的姿态均进行主动控制。

编队内第i个从星相对于主星的姿态运动学方程为：

其中qri为从星本体系相对于主星本体系的姿态四元数；ωri为相应的姿态角速度，其定义如下：

其中Aic为主星本体系到从星本体系的转换矩阵；ωc是主星姿态角速度。

将主星的电磁力矩与控制力矩之和记为Tc，从星的电磁力矩与控制力矩之和记为Ti，从星相对于主星的姿态动力学方程可写作：

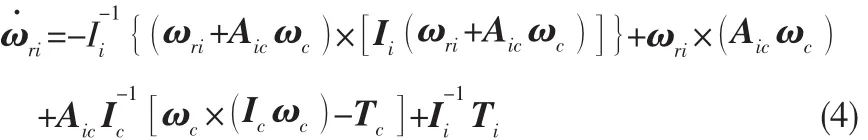
当Ic=Ii=I=diga[I1,I2,I3]满足I1=I2=I3时，可定义等效合控制力矩 T△ri，其形式为：

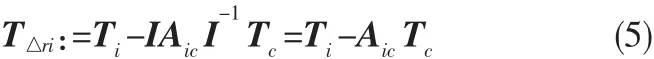
控制量T△ri的引入能保证电磁耦合效应的充分利用，将电磁力矩视为控制力矩的一部分，而不是干扰力矩；此外，T△ri内含有Ti和Tc这两个控制量，这涉及到姿态控制的分配问题，即角动量分配问题，因此可以将相对姿态的控制问题视作最优控制问题，进行求解。忽略下标的ri，可以得到以相对姿态四元

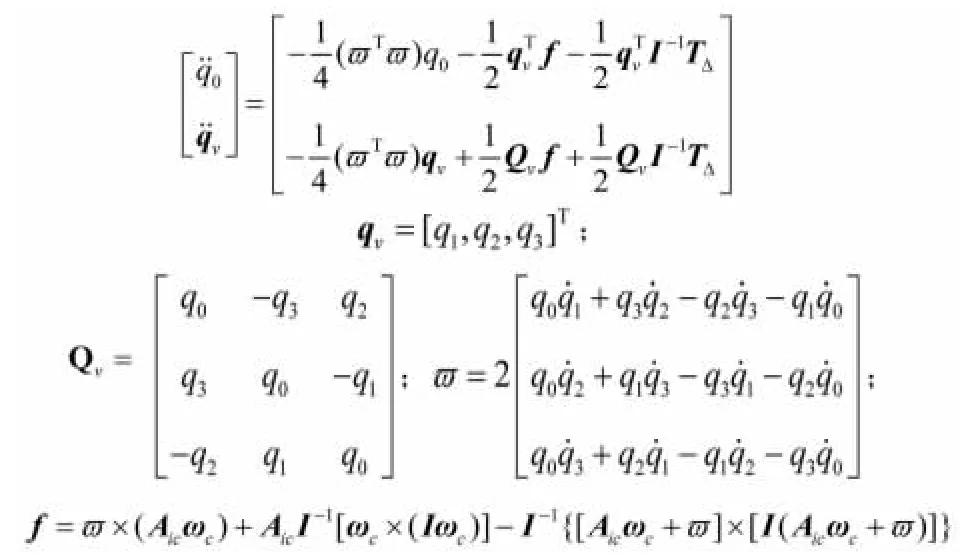
数的二阶形式描述的从星相对于主星的姿态动力学方程：

由于如式(6)所示的动力学方程形式复杂，具有很强的非线性。为了求解角动量分配问题的方便，此处将先采用非线性反馈控制，将相对姿态动力学模型写为状态误差的形式，再进行最优控制问题的求解。由于姿态四元数存在归一化的约束，对姿态进行控制时，只需对相对姿态四元数的矢部qv进行控制，定义状态误差为e=qv-qvd=qv，则姿态控制系统的控制目标转化为设计控制律，使e→0得；当等效合控制力矩T△选取为时，相对姿态的误差模型形式如下：

当选择合适的控制参数矩阵Kp和Kd时，可以保证上式所描述的误差动力学模型是指数稳定的；当考虑有界干扰时，能够保证该误差模型是渐进稳定的，即当t→0时，e→0→0。该证明过程在此不赘述。

1.3 六自由度相对动力学模型

对于考虑姿轨耦合效应的动力学模型，将x=[rT,eT]T和u=[aT,T△T]T作为状态变量和控制变量，则六自由度相对动力学模型可写为如下形式：

其中：

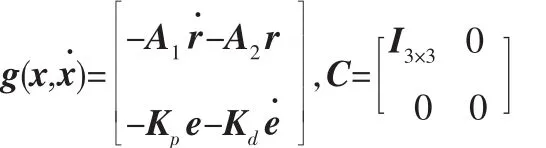
本文只对六自由度动力学中的相对姿态动力学采用了非线性反馈控制，将其写为状态误差的形式，从而便于系统角动量分配这一最优控制问题的求解。在下一章中将基于此动力学模型，利用最优控制理论，规划相对运动轨迹。

2 伪谱法

电磁编队的相对运动轨迹规划可以表述成一个非线性的、带有控制约束、始末状态约束和动力学约束的最优控制问题，即泛函的条件极值问题。本文利用勒让德伪谱法将连续问题离散化，转化为非线性规划问题，并采用相应的高精度数值算法进行求解。

由于电磁编队系统存在很强的非线性和耦合性，常规的数值算法并不适用，因此本文采用高精度的数值求解算法，求解电磁编队的重构轨迹规划问题，该算法也可应用于其他最优控制问题的求解。

上文所描述的有约束的最优控制问题首先通过增广拉格朗日乘子法转化为无约束非线性规划问题，得到包含性能函数和约束条件的乘子罚函数。通过不断修改搜索方向和搜索步长，修正状态空间，使得乘子罚函数最小。其中搜索方向是由罚函数的梯度和Hessian矩阵决定，由单一算法生成的Hessian矩阵有可能不稳定，因此本文采用了复合DFP算法，该算法在Davidon-Fletcher-Powell(DFP)算法和 Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法间进行切换；与单一算法相比，该复合算法能达到更高的精度、更快的收敛速度和更少计算量。搜索步长由改进的模式搜索法确定，需要说明的是，由于罚函数的导数十分复杂，其他搜索方法，如黄金分割搜索法和立方插值法等，并不适用于该问题，计算效果均不理想。综上，求解非线性规划问题的流程如图1所示。

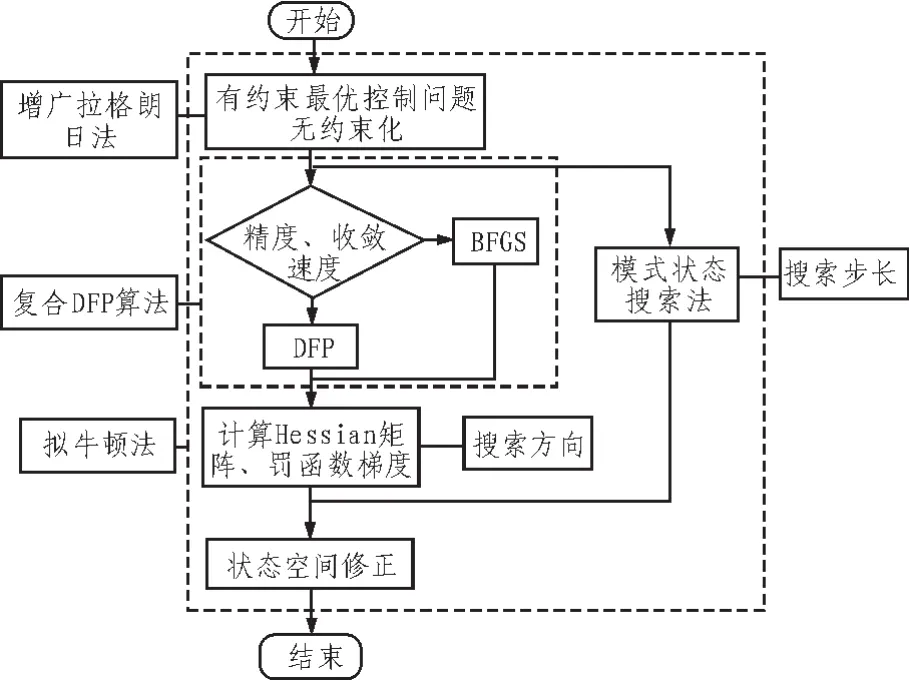
图1 求解非线性规划问题的流程Fig.1 Procedures to solve nonlinear program problem

3 仿真算例

对于三星编队，将卫星3选作“自由星”，其控制磁矩选作。仿真中的参数选取见表1。

相对位置的始、末标称状态选取如下：

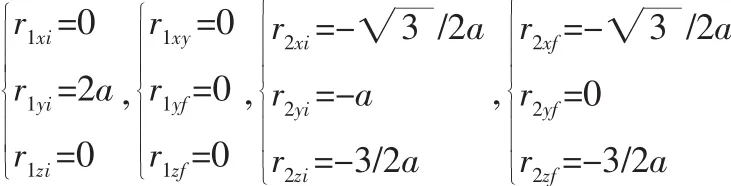
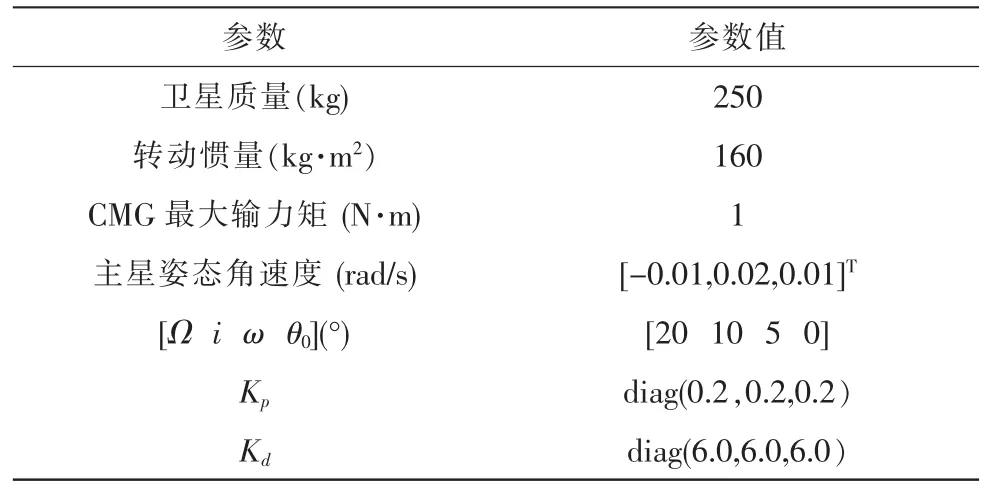
表1 仿真参数Tab.1 Simulation parameters

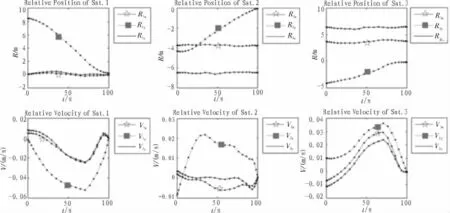
图2 电磁编队的相对位置和速度Fig.2 Relative position and velocity

图3 电磁编队的相对姿态四元数Fig.3 Relative quaternion

4 结论

为了实现电磁编队六自由度的协同控制，本文应用了电磁力和电磁力矩的耦合效应，建立了姿轨耦合动力学模型。通过勒让德伪谱法将编队轨迹的重构问题转化为最优控制问题，由于系统存在很强的非线性和耦合性，本文对数值解法提出改进，仿真结果验证了该方法的有效性。本文所提出的数值解法可推广用于其他最优问题的求解。

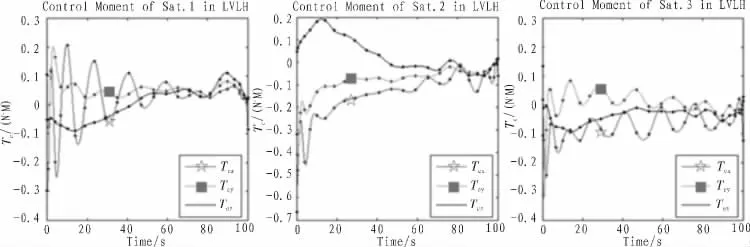
图4 电磁编队的控制力矩Fig.4 Control torque

[1]Kong,E.M.C.,Kwon,D.W.,Schweighart,S.A.,Elias,L.M.,Sedwick,R.J.,and Miller,D.W.Electromagnetic Formation Flight for Multisatellite Arrays[J].Journal of Spacecraft and Rockets,2004,41(4):659-666.

[2]Umair A,David W M,Jaime L R.Control of electromagnetic satellite formations in Near-earth orbits[J].Journal of guidance,control,and dynamics,2010,303(6):1883-1891.

[3]Eslinger G J,Saenz-Otero A.Electromagnetic formation flight control using dynamic programming[J].American Astronautical Society Rocky Mountain Chapter,2013.

[4]Elias L M,Kwon D W,Sedwick R J,et al.Electromagnetic formation flight dynamics including reaction wheel gyroscopic stiffening effects[J].Journal of guidance,control,and dynamics,2007,30(2):499-511.

[5]SU J,DONG Y.Sliding mode variable structure control for electromagnetic satellite formation station-tracking[J].Journal of Astronautics,2011(5):21.

[6]Ahsun U,Miller D W.Dynamics and control of electromagnetic satellite formations[C]//American Control Conference,2006.