基于盲源分离的共形阵列二维DOA估计

王法栋，李杰然，王瑞革

（中国人民解放军92785部队，河北秦 皇岛 066200）

共形阵列是一种与载体表面共形的天线阵列。一般来说，共形阵列具有安装简化、波束扫描范围广、RCS小等优点[1]。目前，现代飞机、导弹、卫星等设备均要求采用共形阵列天线。因此，共形阵列的相关研究已受到广泛关注。从阵列信号处理角度讲，参数估计问题是共形阵列的主要问题之一。国内外学者围绕共形阵列的优势，在共形阵列信号波达方向估计（direction of arrival，DOA）计方面做了一些研究工作[2-7]。比如文献[2]以圆柱共形阵列为例，采用多维MUSIC谱估计方法实现了DOA估计，但其需要二维谱峰搜索，运算量大，不适用于工程实际；文献[3-6]通过合理划分阵列使其满足旋转不变结构，从而实现柱面阵列和锥面共形阵列的DOA合估计。但其方法对阵列形状要求高，并不能适用于其他共形阵列。可以说，关于共形阵列DOA估计问题还有许多值得进一步研究的工作。本文试图给出一种对阵列形状限制小，估计性能良好，运算量小的共形阵列DOA估计方法。盲源分离用于阵列信号DOA估计是近几年出现的方法[7]，其利用信号的统计独立性实现信号的DOA估计。结合盲源分离的特点，本文利用JADE算法实现了共形阵列信号DOA估计。以圆台共形阵列为例，对算法性能做了仿真验证。

1 阵列结构与数据模型

共形阵列没有具体的阵列形状，这里为了体现算法普适性，采用结构任意的阵列，如图1所示。阵元数为N，第n个阵元的坐标为（pnx，pny，pnz）。

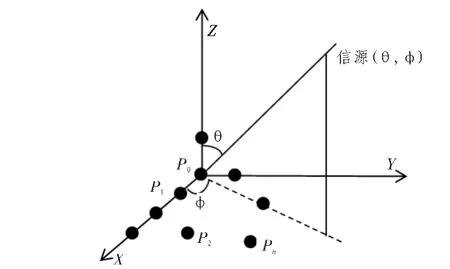
图1 任意形状阵列Fig.1 Arrays of arbitrary shape

假设有K个已知载频为ω0，波长为λ的不相关窄带信源 s1（t），s2（t），…，sK（t）入射到阵列，其入射角分别为{（θ1，φ1），（θ2，φ2），…，（θK，φK）}。 设每个阵元的极化辐射方向图相同，但对于曲率较大的共形阵列而言，各阵元实际接收数据时会有所不同。可以参考文献[1]的共形阵列建模的方法，记gn（θk，φk）为第n个阵元实际接收方向图。

第n个阵元的输出为：

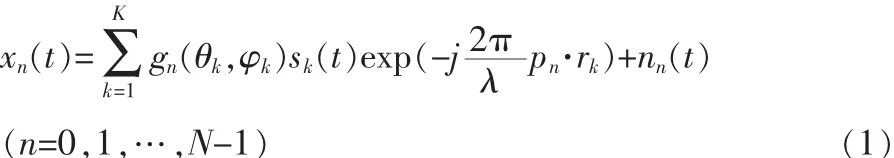
其中，sk（t）为第 k 个入射信号，其中|Ek|为幅度，Ψk为[0，2π]内均匀分布的初始相位；rk为第k个信号的传播矢量

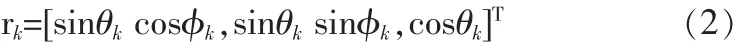
nn（t）为加性噪声矢量，其均值为零，且各阵元间互不相关。

式（1）可写成矢量的形式

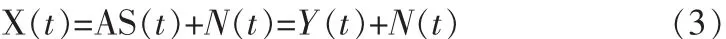
其中，

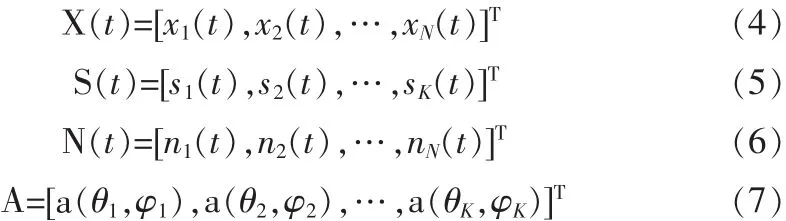
2 JADE算法共形阵列信号DOA估计

将盲源分离技术应用到阵列信号DOA估计是近些年出现的方法。一般而言，可以采用基于信息论的方法、基于二阶统计的方法和基于高阶累计量的方法等。JADE算法是由Cardoso提出的一种盲源分离算法。其引入数据四阶累积量矩阵组，通过对其做特征分解进行联合对角化，实现信号的盲分离。考虑JADE算法结果具有稳健的特点，本文采用JADE算法实现共形阵列信号DOA估计。

通常认为，阵元数N大于信号源数K，即有N>K。为了估计信号源个数，JADE算法首先要对阵列接收数据x（t）做白化处理，这样可以消除各通道接收数据间的二阶相关。

假设白化矩阵为W，则白化处理即是使输出Z=WY的各分量zk（t）的方差为1，且互不相关。假设信号方差均为1，则有

这样，可以得到

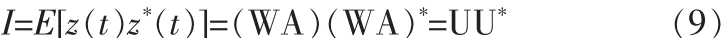
式中U=WA是个酉矩阵。

那么，流形矢量矩阵A可以由假设白化矩阵为W和酉矩阵U得到：

其中，“#”表示求伪逆。

可以看到如果求出酉矩阵U，就可获得流形矢量矩阵A的估计，从而可以实现对信号DOA估计。

令白化后的数据 Z为 Z=[z1，z2，…，zK]，则 Z的四阶累计累积量为

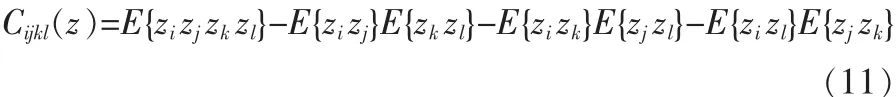
记变换矩阵的第（i，j）个元素为 Fij，则

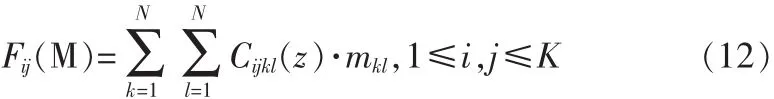
其中，mkl是矩阵 M 的第 k，l元素。 可以证明，F（M）是对称矩阵。那么，F（M）可以分解为

式中，λ为特征值，M为特征矩阵。这样，F（M）可表示为

其中，

可以发现，U矩阵起到将F（M）对角化的作用。如果各信号的特征值不相同，就能得到酉矩阵的估计，利用式（10）即可得到流形矢量矩阵的估计，进而实现对信号的DOA估计。由于通过JADE分离得到的信号顺序是不确定的，需要对分离得到的信号进行FFT，以确定信号频率。

下面给出算法的具体实现步骤：

1）对接收收据做白化处理，求得白化矩阵W；

2）选择矩阵组M，利用白化后的数据求得四阶累积量F（M）；

3 仿真实验

实验1采用如图2所示的17阵元的圆台阵共形阵列，圆台顶层半径R=λ/4，圆台底角为60°。共分4层，两层阵元间距dz=λ/4。每层阵元等角度分布，其相邻阵元夹角30°。阵元采用有向阵元，即

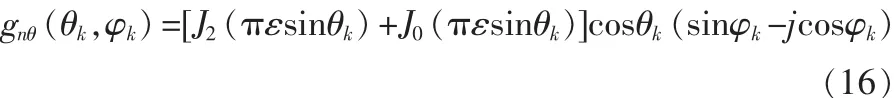
其中，J0（πεsinθk）和 J2（πεsinθk）分别为零阶和二阶第一类贝塞尔函数。ε是由天线阵元位置和工作状态决定的可变参数，取 ε=0.5。

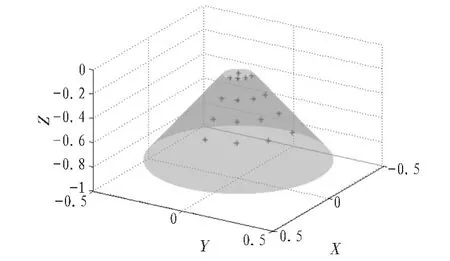
图2 共形阵列Fig.2 Conformal array

设有2个频率为f0的空间窄带信号源入射到阵列，其参数（θ，φ）（其中，θ代表俯仰角，φ 代表方位角）为（30°，40°）和（30°，50°），信噪比（SNR）均为 20 dB，采样快拍数为 500，做50次蒙特卡罗仿真实验。图3给出了二维角度的估计结果。

从图3看出，本文给出的算法可以有效地估计出信源的二维角度。算法对阵列形状限制小，几乎可以适用于任意共形阵列。

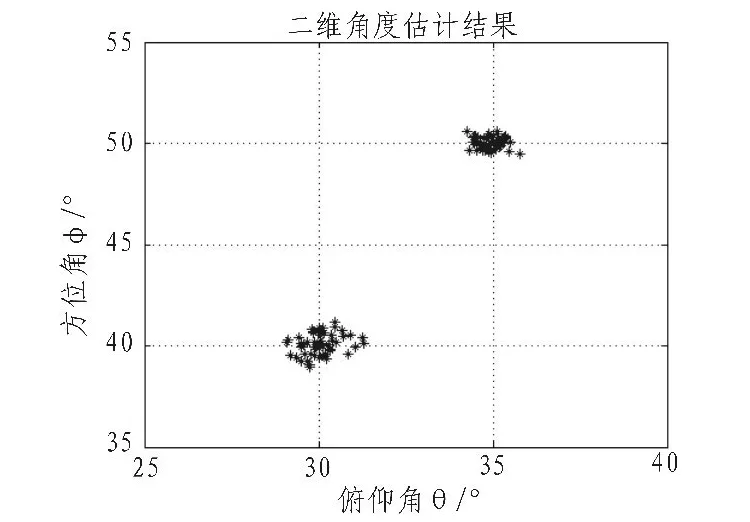
图3 二维角度估计结果Fig.3 The result of DOA

实验2阵列与信源设置同实验1，采用500次快拍，进行50次独立实验，图4给出了2个信源二维角度估计结果的均方根误差（RMSE）随信噪比的变化曲线。

定义信源k的二维角度估计的均方根误差为

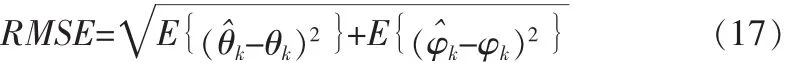
由图4可以看出，随着SNR的增加，算法估计的均方根误差逐渐减小，估计的精度逐渐提高。

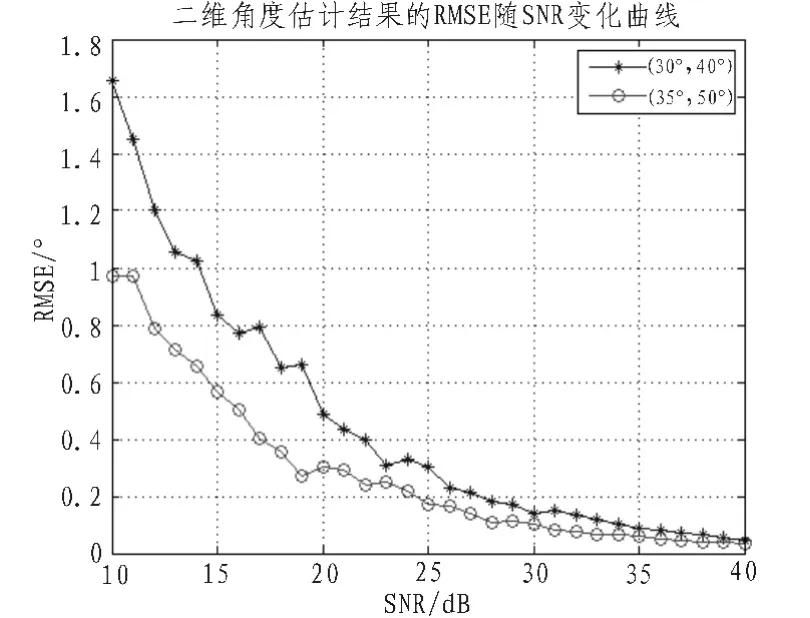
图4 二维角度估计结果的RMSE随SNR变化曲线Fig.4 DOA RMSE versus SNR

实验3 阵列与信源设置同实验1，信噪比为20 dB，进行50次独立实验，图5给出了2个信源二维角度估计结果的均方根误差（RMSE）随采样快拍数的变化曲线。

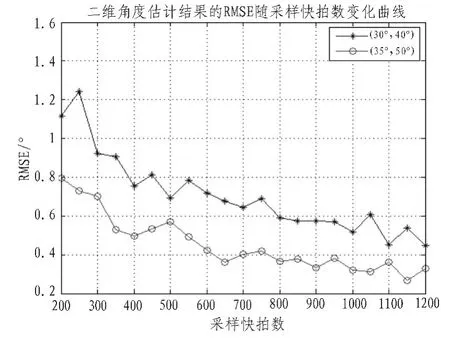
图5 二维角度估计结果的RMSE随采样快拍数变化曲线Fig.5 DOA RMSE versus number of snapshots

由图5可以看出，随着采样快拍数的增加，算法估计的均方根误差逐渐减小，估计的精度逐渐提高。

4 结束语

本文利用盲源分离技术，给出了基于JADE盲源分离的共形阵列信号DOA估计算法。以圆台共形阵列为例，通过仿真实验对算法有效性进行了验证。算法对阵列形状限制小，性能良好。关于共形阵列信号参数估计还有许多要做的工作，比如共形阵列信号极化、频率参数估计问题等，还有许多值得继续深入研究的工作。

[1]Zou L，Lasenby J，He Z.Direction and polarisation estimation using polarised cylindrical conformal arrays [J].Signal Processing， IET，2012，6（5）：395-403.

[2]齐子森，郭英，王布宏，等.共形阵列天线 MUSIC算法性能分析[J].电子与信息学报，2008，30（11）:2674-2677.QI Zi-sen，GUO Ying，WANG Bu-hong，et al.Performace analysis of MUSIC for conformal array[J].Journal of Electronics&Information Technology，2008，30（11）:2674-2677.

[3]郭英，高梅，张树银，等.基于旋转不变子空间原理的共形阵列 DOA与极化状态联合估计 [J].上海交通大学学报，2013，47（7）:1137-1142.GUO Ying，GAO Mei，ZHANG Shu-yin，et al.DOA and polarization estimation with conformal array based on ESPRIT[J].Journal of Shanghai Jiao tong University，2013，47（7）:1137-1142.

[4]Yang P，Yang F，Nie Z P.DOA estimation with sub-array divided technique and interporlated esprit algorithm on a cylindrical conformal array antenna[J].Progress In Electromagnetics Research，2010（103）:201-216.

[5]张树银，郭英，齐子森.锥面共形阵列信源方位和极化参数的联合估计算法 [J].电子与信息学报，2011，33（10）：2407-2412.ZHANG Shu-yin，GUO Ying，QI Zi-sen.Joint estimation of 2D DOA and polarization with conical conformal array antenna[J].Journal of Electronics&Information Technology，2011，33（10）:2407-2412.

[6]Si W，Wan L，Liu L，et al.Fast estmation of frequency and 2-D doas for cylindrical conformal array antenna using state-space and propagator method[J].Progress In Electromagnetics Research，2013（137）:51-71.

[7]杨阳，李辉，万坚，等.一种自适应盲分离调频信号的方法[J].通信技术，2008，41（12）:20-22.YANG Yang，LI Hui，WAN Jian，et al.An adaptive blind separation method for frequency-hopping signals[J].Communications Technology，2008，41（12）:20-22.