基于多层小波变换的压缩感知图像快速复原算法研究

曹利红，徐志京

（上海海事大学 信息工程学院，上海 201306）

图像复原技术的发展始于二十世纪五十年代的空间探索，人们期待有一种技术能够弥补和找回由于图像获取以及传输系统不完善而造成的图像降质。任何一种因素造成的图像降质都会降低科学价值，同时也是巨大的经济损失。因此，“数字图像复原”技术应运而生。现代图像复原技术理论与实际应用上都较为成熟，根据数据处理域的不同可以分为基于时域、基于频域和基于小波域的方法等。

常用的频域方法主要有：逆滤波法、Wiener滤波法、约束最小二乘法；时域方法主要有：凸集投影法、最大熵复原算法、受限制自适应复原算法。

近年来，一种新型信息处理理论——压缩感知理论又称压缩传感理论 （Compressed Sensing or Compressed Sampling，CS）出现，它是由著名的数学家D.Donoho与E.Candes在2006年提出的[1-2]。压缩感知理论突破了传统Nyquist信号采样定理的限制，它指出，只要信号是可压缩的或在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上，然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号，可以证明这样的投影包含了重构信号的足够信息。在该理论框架下，采样速率不决定于信号的带宽，而决定于信息在信号中的结构和内容。

压缩感知信号重构部分与图像复原都要解决“反问题”[3]，这很自然让人联想到是否可以将压缩感知理论运用于图像复原领域。事实证明，基于压缩感知理论的图像复原效果优于传统图像复原方法，且降低了算法复杂度，节约了存储空间与传输成本，这使得压缩感知理论在图像复原领域具有良好的应用前景。目前压缩感知理论已经在图像复原领域得到了初步应用，例如，基于图像复原领域ROF模型[4]的总变分重构方法和已应用于图像复原领域的迭代阈值法等。

文中将建立基于压缩感知的图像复原模型，选取小波基作为变换基，高斯随机测量矩阵作为观测矩阵，OMP算法作为信号重构算法对图像进行复原，并用MATLAB进行仿真，对比传统图像复原和基于压缩感知理论的图像复原效果。

1 压缩感知原理简介

压缩感知理论主要分成3个核心步骤：稀疏性变换、观测矩阵设计、信号重构算法设计。如图1为基于压缩感知理论的信号重构过程框图。

图1 基于压缩感知理论的信号重构过程框图Fig.1 Structure diagram of compressed sensing signal reconstruction

设有一信号（X∈RN），可以作 N×1 维列向量，元素为[n]，n=1，2，…，N。若RN空间的任何信号都可以用N×1维的正交基向量{Ψi}Ni=1的线性组合表示，把向量{Ψi}Ni=1作为列向量形成N×N维的基矩Ψ=[Ψ1，Ψ2，…ΨN]，于是任何信号X都可表示为：

其中Θ是投影系数。显然，X和Θ是同一个信号的等价表示，是信号在时域的表示，Θ则是信号在Ψ域的表示。如果的非零个数K比N小很多（即K＜＜N），则表明该信号在域是可压缩的（也称稀疏的）。可以用一个与变换基Ψ不相关的观测基Φ（M×N维，且M＜＜N）对系数向量进行线性变换，并得到M×1维观测集合Y，其中

信号的稀疏表示和观测过程也可以表示为信号X通过矩阵ACS进行非自适应观测，即有

其中，ACS称为CS信息算子。

当 ACS满足 RIP（restricted isometric property）等距约束条件[5]，从观测集合Y中重构原始信号X则转化为一个优化问题：

2 基于压缩感知的图像复原模型

图像复原关键问题是要建立退化模型。假设f（x，y）为原始图像，g（x，y）为退化图像，（x，y）为复原图像，n（x，y）为噪声，H[·]是综合所有退化因素的系数，则图像退化和复原过程的空间域模型如图2所示。

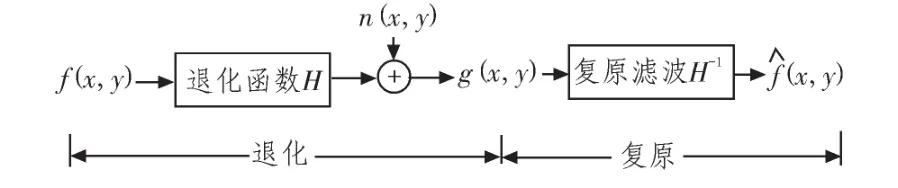
图2 图像退化和复原模型Fig.2 Model of image degradation and recovery

基于压缩感知的图像复原模型如图3所示。

图3 基于压缩感知理论的图像复原模型Fig.3 Model of image degradation and recovery based on compressed sensing

根据压缩感知理论，用测量矩阵Φ对退化图像g（x，y）进行频域随机测量，之后经过反卷积复原图像。在此，我们考虑图像退化模型

其中，Φ∈RK×N，K＜＜N 被称为 CS 观测矩阵。

从K×1维的观测信号y中复原N×1维的信号f是一个不确定系统，然而，压缩感知理论表明，如果信号f在Ψ域能进行稀疏变换并且观测矩阵与稀疏变换基不相关，我们就可以从小部分非完整观测数据中精确或者高概率重构信号[6]。由此，我们得到

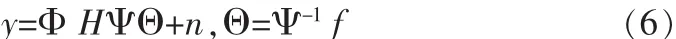
其中，Ψ－1是一个快速稀疏变换，Ψ而是它的逆。这就是基于压缩感知理论的图像退化模型。

那么基于压缩感知理论的图像复原模型为：

即图像的复原中要解决的反变换问题转化成了压缩感知的信号重构问题，这大大减少了采样数据，节约了存储空间。

3 实验仿真与结果说明

为了验证本文所提算法对退化图像复原的有效性和实用性，对大量退化图像进行了仿真实验，以下是部分实验结果。以MATLAB2008a为仿真软件，稀疏基选择离散小波基，观测矩阵选择高斯随机测量矩阵，重构算法选择OMP算法。

首先以大小为的灰度图像Lena为例，在原始图像中加入均值为0，方差为0.001的高斯白噪声，生成含噪图像如图4（a）所示，分别用高斯滤波、维纳滤波以及本文所提CS图像复原方法（其中采样点数M=190）对退化图像进行重构，结果分别如图 4（b）、4（c）、4（d）所示。

图4 含噪图像以及复原图像Fig.4 Blurred image and recovered image

其次，对混杂了高斯白噪声的Lena、Cameraman、Barbara经典图像分别用高斯滤波、维纳滤波以及CS图像复原方法（M=190）进行复原，分别测得的PSNR结果如表1。

根据表2，对比不同退化图像在不同复原方法下的PSNR值，基于压缩感知的复原图像质量高于传统的图像复原质量。压缩感知理论降低了图像的采集量，避免了存储空间的浪费并提高了传输效率，同时又能有效地实现图像重构。

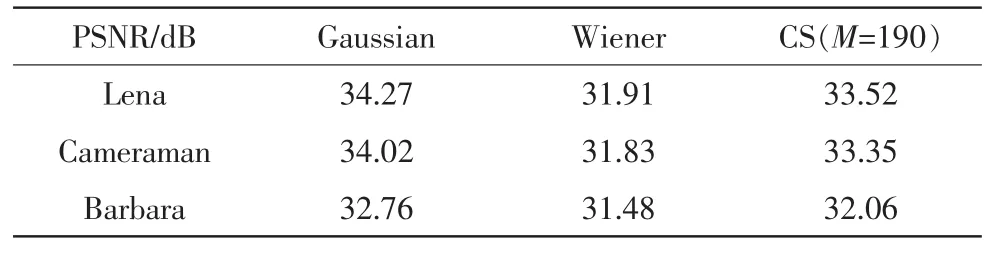
表1 三种退化图像不同复原方法的PSNRTab.1 PSNR of three kinds of recovered method for degraded image

接下来，对由于“运动模糊”造成退化的图像就行仿真研究，对比不同复原方法的优劣性。依旧以大小为256*256的灰度图像Lena为例，将原始图像通过均衡滤波器，使图像产生模糊，结果如图5（a）所示。分别用高斯滤波、维纳滤波以及本文所提CS图像复原方法（其中采样点数M=190）对退化图像进行重构，结果分别如图 5（b）、5（c）、5（d）所示。

图5 含噪图像以及复原图像Fig.5 Blurred image and recovered image

依旧对通过均衡滤波器模糊了的 Lena、Cameraman、Barbara经典图像分别用高斯滤波、维纳滤波以及CS图像复原方法（M=190）进行复原，分别测得的PSNR结果如表2。

表2 三种退化图像不同复原方法的PSNRTab.2 PSNR of three kinds of recovered method for degraded image

根据表2，对比不同退化图像在不同复原方法下的PSNR值，基于压缩感知的复原图像质量高于传统的图像复原质量。压缩感知理论降低了图像的采集量，避免了存储空间的浪费并提高了传输效率，同时又能有效地实现图像重构。

最后，文献[7]定义了“峰值信噪比-采样率”（“PSNRSampling Rate”）曲线，用于说明图像复原质量与测量矩阵观测数据量的关系。本文以Lena图像为例，稀疏基选择离散小波基，观测矩阵选择高斯随机测量矩阵，重构算法选择OMP算法，对应不同采样率（压缩感知理论框架下采样率定义为M/N）下图像复原PSNR走势如图6所示。

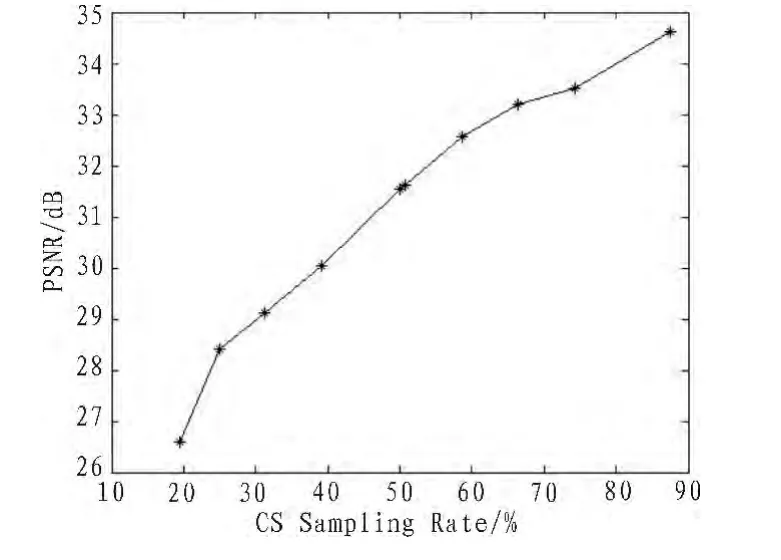
图6 图像复原的压缩感知"峰值信噪比-采样率"曲线（Lena图）Fig.6 "PSNR-Sampling Rate"curve of compressed sensing image recovery （Lena image）

由图6可以看出，随着采样率的增大，复原图像的PSNR值逐渐提高，变化程度趋于稳定。

4 结 论

文中将基于小波变换的压缩感知理论应用于图像复原领域，提出了基于小波变换的压缩感知图像快速复原算法模型，打破了传统信号采样受Nyquist采样定理的限制，通过信号的稀疏变换来实现采样和压缩，大大降低了图像存储与传输成本，提高了图像复原效率与主客观复原质量。通过

Matlab实验仿真，结果表明，本文所提图像复原可以仅从较少的稀疏性观测结果中对退化图像进行高概率复原并获得了较好的复原效果，并且可以通过减少OMP重构算法的迭代次数等方法来实现复原速度的提升。

[1]Donoho D.Compressed Sensing[J].IEEE Transactions on Information Theory，2006，52（4）:1289-1306.

[2]Candès E，RombergJ，Tao T.Robust uncertaintyprinciples:Exact signal reconstruction from highly incompletefrequency information[J].IEEETrans.Inform.Theory，2006，52（2）:489-509.

[3]JING Li-chen，TAN Shan.Development and prospect of image multiscale geometric analysis[J].Acta Electronica Sinica，2003，31（12A）：1975-1981.

[4]北京大学数学系几何与代数教研室前代数小组.高等代数[M].3版.北京：高等教育出版社，2003.

[5]Candès E，Tao T.Decoding by linear programming[J].IEEE Trans.Inf.Theory，2005，51（12）:4203-4215.

[6]Candès E，Romberg J，Tao T.Stable signal recovery from incomplete and inaccurate measurement[J].Commun.Pure Appl.Math.，2006，59（8）:1207-1223.

[7]Fiqueiredo M A T，Nowak R D，wheat SJ.Gradient projection for sparsereconstruction：application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing，2007，1（4）：586-598.